GPU 硬件原理架构（一）

id="article_content" class="article_content clearfix"> id="content_views" class="htmledit_views">

这张费米管线架构图能看懂了，整个GPU的架构基本就熟了。市面上有很多GPU厂家，他们产品的架构各不相同，但是核心往往差不多，整明白一了个基本上就可以触类旁通了。下面这张图信息量很大，可以结合博客GPU 英伟达GPU架构回顾-CSDN博客一点点看。

费米架构管线图

1. GPU概念

GPU 是 Graphics Processing Unit（图形处理器）的简称，它是计算机系统中负责处理图形和图像相关任务的核心组件。GPU 的发展历史可以追溯到对计算机图形处理需求的不断增长，以及对图像渲染速度和质量的不断追求。从最初的简单图形处理功能到如今的高性能计算和深度学习加速器，GPU 经历了一系列重要的技术突破和发展转折。

在接下来的内容中，除了给出GPU硬件基本概念，还将探讨 GPU 与 CPU 的区别，了解它们在设计、架构和用途上存在显著差异。此外，我们还将简短介绍一下 AI 发展和 GPU 的联系，并探讨 GPU 在各种领域的应用场景。

除了图形处理和人工智能，GPU 在科学计算、数据分析、加密货币挖矿等领域也有着广泛的应用。深入了解这些应用场景有助于我们更好地发挥 GPU 的潜力，解决各种复杂计算问题。现在让我们深入了解 GPU 的发展历史、与 CPU 的区别、AI 所需的重要性以及其广泛的应用领域。

1.1 GPU背景

GPU，全称是Graphics Processing Unit。在最开始的时候，它的功能与名字一致，是专门用于绘制图像和处理图元数据的特定芯片。在没有GPU的时候，人们想将计算机中的数据显示在屏幕上，是使用CPU来进行相关运算的。我们要做的事情简单概括一下，就是通过对数据进行相应的计算，把数据转换成一个又一个图片上的像素，然后将这张图片显示在屏幕上。整个流程中的计算并不复杂，但是数量大，且计算流程重复，如果全盘交给CPU的话会给其造成很大的性能负担。于是乎GPU诞生了。

在GPU出现以前，显卡和CPU的关系有点像“主仆”，简单地说这时的显卡就是画笔，根据各种有CPU发出的指令和数据进行着色，材质的填充、渲染、输出等。较早的娱乐用的3D显卡又称“3D加速卡”，由于大部分坐标处理的工作及光影特效需要由CPU亲自处理，占用了CPU太多的运算时间，从而造成整体画面不能非常流畅地表现出来。

例如，渲染一个复杂的三维场景，需要在一秒内处理几千万个三角形顶点和光栅化几十亿的像素。早期的3D游戏，显卡只是为屏幕上显示像素提供一个缓存，所有的图形处理都是由CPU单独完成。图形渲染适合并行处理，擅长于执行串行工作的CPU实际上难以胜任这项任务。所以，那时在PC上实时生成的三维图像都很粗糙。不过在某种意义上，当时的图形绘制倒是完全可编程的，只是由CPU来担纲此项重任，速度上实在是达不到要求。

随着时间的推移，CPU进行各种光影运算的速度变得越来越无法满足游戏开发商的要求，更多多边形以及特效的应用榨干了几乎所有的CPU性能，矛盾产生了······

那么，GPU的工作原理是什么？

简单的说GPU就是能够从硬件上支持T&L（Transform and Lighting，多边形转换与光源处理）的显示芯片，因为T&L是3D渲染中的一个重要部分，其作用是计算多边形的3D位置和处理动态光线效果，也可以称为“几何处理”。一个好的T&L单元，可以提供细致的3D物体和高级的光线特效；只不过大多数PC中，T&L的大部分运算是交由CPU处理的（这就也就是所谓的软件T&L），由于CPU的任务繁多，除了T&L之外，还要做内存管理、输入响应等非3D图形处理工作，因此在实际运算的时候性能会大打折扣，常常出现显卡等待CPU数据的情况，其运算速度远跟不上今天复杂三维游戏的要求。即使CPU的工作频率超过 1GHz或更高，对它的帮助也不大，由于这是PC本身设计造成的问题，与CPU的速度无太大关系。

1.2 GPU发展历史

在 GPU 发展史上，第一代 GPU 可追溯至 1999 年之前。这一时期的 GPU 在图形处理领域进行了一定的创新，部分功能开始从 CPU 中分离出来，实现了针对图形处理的硬件加速。其中，最具代表性的是几何处理引擎，即 GEOMETRY ENGINE。该引擎主要用于加速 3D 图像处理，但相较于后来的 GPU，它并不具备软件编程特性。这意味着它的功能相对受限，只能执行预定义的图形处理任务，而无法像现代 GPU 那样灵活地适应不同的软件需求。

然而，尽管功能有限，第一代 GPU 的出现为图形处理领域的硬件加速打下了重要的基础，奠定了后续 GPU 技术发展的基石。

第二代 GPU 的发展跨越了 1999 年到 2005 年这段时期，其间取得了显著的进展。1999 年，英伟达发布了 GeForce256 图像处理芯片，这款芯片专为执行复杂的数学和几何计算而设计。与此前的 GPU 相比，GeForce256 将更多的晶体管用于执行单元，而不是像 CPU 那样用于复杂的控制单元和缓存。它成功地将诸如变换与光照（TRANSFORM AND LIGHTING）等功能从 CPU 中分离出来，实现了图形快速变换，标志着 GPU 的真正出现。

随着时间的推移，GPU 技术迅速发展。从 2000 年到 2005 年，GPU 的运算速度迅速超越了 CPU。在 2001 年，英伟达和 ATI 分别推出了 GeForce3 和 Radeon 8500，这些产品进一步推动了图形硬件的发展。图形硬件的流水线被定义为流处理器，顶点级可编程性开始出现，同时像素级也具有了有限的编程性。

尽管如此，第二代 GPU 的整体编程性仍然相对有限，与现代 GPU 相比仍有一定差距。然而，这一时期的 GPU 发展为后续的技术进步奠定了基础，为图形处理和计算领域的发展打下了坚实的基础。

从长远看，英伟达的 GPU 在一开始就选择了正确的方向 MIMD，通过 G80 Series，Fermi，Kepler 和 Maxwell 四代（下一章节会有解析）大跨步进化，形成了完善和复杂的储存层次结构和指令派发/执行管线。ATI/AMD 在一开始选择了 VLIW5/4，即 SIMD，通过 GCN 向 MIMD 靠拢，但是进化不够完全（GCN 一开始就落后于 Kepler），所以图形性能和 GPGPU 效率低于对手。

英伟达和 ATI 之争本质上是 shader 管线与其他纹理，ROP 单元配置比例之争，A 认为计算用 shader 越多越好，计算性能强大，N 认为纹理单元由于结构更简单电晶体更少，单位面积配置起来更划算，至于游戏则是越后期需要计算的比例越重。

第三代 GPU 的发展从 2006 年开始，带来了方便的编程环境创建，使得用户可以直接编写程序来利用 GPU 的并行计算能力。在 2006 年，英伟达和 ATI 分别推出了 CUDA（Compute Unified Device Architecture）和 CTM（CLOSE TO THE METAL）编程环境。

这一举措打破了 GPU 仅限于图形语言的局限，将 GPU 变成了真正的并行数据处理超级加速器。CUDA 和 CTM 的推出使得开发者可以更灵活地利用 GPU 的计算能力，为科学计算、数据分析等领域提供了更多可能性。

2008 年，苹果公司推出了一个通用的并行计算编程平台 OPENCL（Open Computing Language）。与 CUDA 不同，OPENCL 并不与特定的硬件绑定，而是与具体的计算设备无关，这使得它迅速成为移动端 GPU 的编程环境业界标准。OPENCL 的出现进一步推动了 GPU 在各种应用领域的普及和应用，为广大开发者提供了更广阔的创新空间。

第三代 GPU 的到来不仅提升了 GPU 的计算性能，更重要的是为其提供了更便捷、灵活的编程环境，使得 GPU 在科学计算、深度学习等领域的应用得以广泛推广，成为现代计算领域不可或缺的重要组成部分。

下图分别展示了英伟达和 AMD 的工具链架构，我们可以看到两者的层次架构都是十分相像的，最核心的区别实则在于中间的 libraries 部分，两家供应商均根据自己的硬件为基础 library 做了优化；此外在编译层面两方也会针对自身架构，在比如调度，算子融合等方面实现各自的编译逻辑；而在对外接口上双方都在争取提供给当今热门的框架和应用以足够的支持。

以及从下方二者的细粒度对比图中，我们更能看出两方工具链架构间的一一映射和具体细节实现上的区别：

1.3 GPU与CPU差异

现在探讨一下 CPU 和 GPU 在架构方面的主要区别， CPU 即中央处理单元（Central Processing Unit），负责处理操作系统和应用程序运行所需的各类计算任务，需要很强的通用性来处理各种不同的数据类型，同时逻辑判断又会引入大量的分支跳转和中断的处理，使得 CPU 的内部结构异常复杂。GPU 即图形处理单元（Graphics Processing Unit），可以更高效地处理并行运行时复杂的数学运算，最初用于处理游戏和动画中的图形渲染任务，现在的用途已远超于此。两者具有相似的内部组件，包括核心、内存和控制单元。下图是GPU与CPU的构成差异图：

上图有几个重点的元素，也是我们下文重点要阐述的概念，绿色代表的是computational units(可计算单元) 或者称之为 cores(核心)，橙色代表memories（内存） ，黄色代表的是control units（控制单元）。因此想要理解GPU的底层核心构成，就必须明确这几个元素的作用，下文会逐一讲解每个元素的作用。

GPU采用了数量众多的计算单元和超长的流水线，但只有非常简单的控制逻辑并省去了Cache。而CPU不仅被Cache占据了大量空间，而且还有有复杂的控制逻辑和诸多优化电路，相比之下计算能力只是CPU很小的一部分。CPU需要很强的通用性来处理各种不同的数据类型，同时又要逻辑判断又会引入大量的分支跳转和中断的处理。这些都使得CPU的内部结构异常复杂。而GPU面对的则是类型高度统一的、相互无依赖的大规模数据和不需要被打断的纯净的计算环境。

GPU 和 CPU 在架构方面的主要区别包括以下几点：

  1. 并行处理能力： CPU 拥有少量的强大计算单元（ALU），更适合处理顺序执行的任务，可以在很少的时钟周期内完成算术运算，时钟周期的频率很高，复杂的控制逻辑单元（Control）可以在程序有多个分支的情况下提供分支预测能力，因此 CPU 擅长逻辑控制和串行计算，流水线技术通过多个部件并行工作来缩短程序执行时间。GPU 控制单元可以把多个访问合并成，采用了数量众多的计算单元（ALU）和线程（Thread），大量的 ALU 可以实现非常大的计算吞吐量，超配的线程可以很好地平衡内存延时问题，因此可以同时处理多个任务，专注于大规模高度并行的计算任务。
  2. 内存架构： CPU 被缓存 Cache 占据了大量空间，大量缓存可以保存之后可能需要访问的数据，可以降低延时； GPU 缓存很少且为线程（Thread）服务，如果很多线程需要访问一个相同的数据，缓存会合并这些访问之后再去访问 DRMA，获取数据之后由 Cache 分发到数据对应的线程。 GPU 更多的寄存器可以支持大量 Thread。
  3. 指令集： CPU 的指令集更加通用，适合执行各种类型的任务； GPU 的指令集主要用于图形处理和通用计算，如 CUDA 和 OpenCL。
  4. 功耗和散热： CPU 的功耗相对较低，散热要求也相对较低；由于 GPU 的高度并行特性，其功耗通常较高，需要更好的散热系统来保持稳定运行。

因此，CPU 更适合处理顺序执行的任务，如操作系统、数据分析等；而 GPU 适合处理需要大规模并行计算的任务，如图形处理、深度学习等。在异构系统中， GPU 和 CPU 经常会结合使用，以发挥各自的优势。

GPU 起初用于处理图形图像和视频编解码相关的工作。 GPU 跟 CPU 最大的不同点在于， GPU 的设计目标是最大化吞吐量（Throughput），相比执行单个任务的快慢，更关心多个任务的并行度（Parallelism），即同时可以执行多少任务；CPU 则更关心延迟（Latency）和并发（Concurrency）。

CPU 优化的目标是尽可能快地在尽可能低的延迟下执行完成任务，同时保持在任务之间具体快速切换的能力。它的本质是以序列化的方式处理任务。 GPU 的优化则全部都是用于增大吞吐量的，它允许一次将尽可能多的任务推送到 GPU 内部。然后 GPU 通过大数量的 Core 并行处理任务。

带宽、延迟与吞吐

处理器带宽（Bandwidth）、延时（Lantency）和吞吐（Throughput）
  • 带宽：处理器能够处理的最大的数据量或指令数量，单位是 Kb、Mb、Gb；
  • 延时：处理器执行指令或处理数据所需的时间，传送一个数据单元所需要的时间，单位是 ms、s、min、h 等；
  • 吞吐：处理器在一定时间内从一个位置移动到另一个位置的数据量，单位是 bps（每秒比特数）、Mbps（每秒兆比特数）、Gbps（每秒千比特数），比如在第 10s 传输了 20 bit 数据，因此在 t=10 时刻的吞吐量为 20 bps。

解决带宽相比较解决延时更容易，线程的数量与吞吐量成正比，吞吐量几乎等于带宽时说明信道使用率很高，处理器系统设计所追求的目标是提高带宽的前提下，尽可能掩盖传送延时，组成一个可实现的处理器系统。

并发与并行

并行和并发是两个在计算机科学领域经常被讨论的概念，它们都涉及到同时处理多个任务的能力，但在具体含义和应用上有一些区别。

  1. 并行（Parallelism）

并行指的是同时执行多个任务或操作，通常是在多个处理单元上同时进行。在计算机系统中，这些处理单元可以是多核处理器、多线程、分布式系统等。并行计算可以显著提高系统的性能和效率，特别是在需要处理大量数据或复杂计算的情况下。例如，一个计算机程序可以同时在多个处理器核心上运行，加快整体计算速度。

2. 并发（Concurrency）

并发指的是系统能够同时处理多个任务或操作，但不一定是同时执行。在并发系统中，任务之间可能会交替执行，通过时间片轮转或事件驱动等方式来实现。并发通常用于提高系统的响应能力和资源利用率，特别是在需要处理大量短时间任务的情况下。例如，一个 Web 服务器可以同时处理多个客户端请求，通过并发处理来提高系统的吞吐量。

因此并行和并发的主要区别如下：

  • 并行是指同时执行多个任务，强调同时性和并行处理能力，常用于提高计算性能和效率。
  • 并发是指系统能够同时处理多个任务，强调任务之间的交替执行和资源共享，常用于提高系统的响应能力和资源利用率。

在实际应用中，并行和并发通常结合使用，根据具体需求和系统特点来选择合适的技术和策略。同时，理解并行和并发的概念有助于设计和优化复杂的计算机系统和应用程序。在实际硬件工作的过程当中，更倾向于利用多线程对循环展开来提高整体硬件的利用率，这就是 GPU 的最主要的原理。

以三款芯片为例，对比在硬件限制的情况下，一般能够执行多少个线程，对比结果增加了线程的请求（Threads required）、线程的可用数（Threads available）和线程的比例（Thread Ration），主要对比到底需要多少线程才能够解决内存时延的问题。从表中可以看到几个关键的数据：

  • GPU（NVIDIA A100）的时延比 CPU （AMD Rome 7742，Intel Xeon 8280）高出好几个倍数；
  • GPU 的线程数是 CPU 的二三十倍；
  • GPU 的可用线程数量是 CPU 的一百多倍。计算得出线程的比例，GPU 是 5.6， CPU 是 1.2~1.3，这也是 GPU 最重要的一个设计点，它拥有非常多的线程为大规模任务并行去设计。
class="table-box">
AMD Rome 7742Intel Xeon 8280NVIDIA A100
Memory B/W(GB/sec)2041431555
DRAM Latency(ns)12289404
Peak bytes per latency24,88812,727628,220
Memory Efficiency0.064%0.13%0.0025%
Threads required1,55672939,264
Threads available2048896221,184
Thread Ration1.3X1.2X5.6X

CPU 和 GPU 的典型架构对比可知 GPU 可以比作一个大型的吞吐器，一部分线程用于等待数据，一部分线程等待被激活去计算，有一部分线程正在计算的过程中。GPU 的硬件设计工程师将所有的硬件资源都投入到增加更多的线程，而不是想办法减少数据搬运的延迟，指令执行的延迟。

相对应的可以把 CPU 比喻成一台延迟机，主要工作是为了在一个线程里完成所有的工作，因为希望能够使用足够的线程去解决延迟的问题，所以 CPU 的硬件设计者或者硬件设计架构师就会把所有的资源和重心都投入到减少延迟上面，因此 CPU 的线程比只有一点多倍，这也是 SIMD（Single Instruction, Multiple Data）和 SIMT（Single Instruction, Multiple Threads）架构之间最大的区别。 CPU 不是通过增加线程来去解决问题，而是使用相反的方式去优化线程的执行速率和效率，这就是 CPU 跟 GPU 之间最大的区别，也是它们的本质区别。

CPU 和 GPU 典型架构图

SIMD (Single Instruction, Multiple Data) 和 SIMT (Single Instruction, Multiple Threads)
SIMD 架构是指在同一时间内对多个数据执行相同的操作，适用于向量化运算。例如，对于一个包含多个元素的数组，SIMD 架构可以同时对所有元素执行相同的操作，从而提高计算效率。常见的 SIMD 架构包括 SSE (Streaming SIMD Extensions) 和 AVX (Advanced Vector Extensions)。
SIMT 架构是指在同一时间内执行多个线程，每个线程可以执行不同的指令，但是这些线程通常会执行相同的程序。这种架构通常用于 GPU (Graphics Processing Unit) 中的并行计算。CUDA (Compute Unified Device Architecture) 和 OpenCL 都是支持 SIMT 架构的 编程模型。
SIMD 适用于数据并行计算，而 SIMT 适用于任务并行计算。在实际应用中，根据具体的计算需求和硬件环境选择合适的架构可以提高计算性能。

1.4 GPU与DSP差异

‌GPU和DSP的主要区别在于它们的设计目的和应用场景。‌ GPU（图形处理单元）主要用于处理大规模并行计算任务，如图形渲染和深度学习，而DSP（数字信号处理器）则专门用于处理高密集型、重复性的数据，如音频、视频和无线通信中的信号处理任务‌12。

在架构方面，GPU采用SIMD（单指令多数据流）架构，能够同时处理多个数据点，非常适合进行大规模并行计算。相比之下，DSP则采用专用的数字信号处理架构，优化了密集型数学运算，如乘法和累加操作，适用于处理连续的数据流‌14。

在性能和应用场景上，GPU的核心计算能力远超通用处理器，特别适合进行大规模并行计算任务，如深度学习和科学计算。而DSP则以其高效能和低功耗的特点，适用于音频、视频和无线通信等领域的信号处理任务‌23。

在指令集和存储结构上，GPU的指令集和存储结构为并行计算进行了优化，而DSP则采用专门的硬件来实现单周期乘法累加操作，并且通常采用哈佛结构，允许同时对程序和数据进行访问，提高了处理效率‌45。

GPU在几个主要方面有别于DSP（Digital Signal Processing，简称DSP（数字信号处理）架构。其所有计算均使用浮点算法，而且目前还没有位或整数运算指令。此外，由于GPU专为图像处理设计，因此存储系统实际上是一个二维的分段存储空间，包括一个区段号（从中读取图像）和二维地址（图像中的X、Y坐标）。此外，没有任何间接写指令。输出写地址由光栅处理器确定，而且不能由程序改变。这对于自然分布在存储器之中的算法而言是极大的挑战。最后一点，不同碎片的处理过程间不允许通信。实际上，碎片处理器是一个SIMD数据并行执行单元，在所有碎片中独立执行代码。

尽管有上述约束，但是GPU还是可以有效地执行多种运算，从线性代数和信号处理到数值仿真。虽然概念简单，但新用户在使用GPU计算时还是会感到迷惑，因为GPU需要专有的图形知识。这种情况下，一些软件工具可以提供帮助。两种高级描影语言CG和HLSL能够让用户编写类似C的代码，随后编译成碎片程序汇编语言。Brook是专为GPU计算设计，且不需要图形知识的高级语言。因此对第一次使用GPU进行开发的工作人员而言，它可以算是一个很好的起点。

Brook是C语言的延伸，整合了可以直接映射到 GPU的简单数据并行编程构造。经GPU存储和操作的数据被形象地比喻成“流”（stream），类似于标准C中的数组。核心（Kernel）是在流上操作的函数。在一系列输入流上调用一个核心函数意味着在流元素上实施了隐含的循环，即对每一个流元素调用核心体。Brook还提供了约简机制，例如对一个流中所有的元素进行和、最大值或乘积计算。

Brook还完全隐藏了图形API的所有细节，并把GPU中类似二维存储器系统这样许多用户不熟悉的部分进行了虚拟化处理。用Brook编写的应用程序包括线性代数子程序、快速傅立叶转换、光线追踪和图像处理。利用ATI的X800XT和Nvidia的GeForce 6800 Ultra型GPU，在相同高速缓存、SSE汇编优化Pentium 4执行条件下，许多此类应用的速度提升高达7倍之多。

对GPU计算感兴趣的用户努力将算法映射到图形基本元素。类似Brook这样的高级编程语言的问世使编程新手也能够很容易就掌握GPU的性能优势。访问GPU计算功能的便利性也使得GPU的演变将继续下去，不仅仅作为绘制引擎，而是会成为个人电脑的主要计算引擎。

2. GPU硬件框架

GPU的基本底层构成，主要是以GPU计算核心 Cores，以及Memory以及控制单元，三大组成要素组成。

GPU整个架构演进可以查看博客GPU 英伟达GPU架构回顾-CSDN博客，这里整合当前最先进的硬件框架来说明硬件关系，具体实例是使用Maxwell框架：

  1.  架构中 GPC（Graphic Processing Cluster）表示图像处理簇，一共有 8 个。共有两个 L2 Cache 并且可以互相实现数据同步，通过 Memory Controller 实现与高带宽存储器 HBM2（High Bandwidth Memory）进行数据交换。
  2. 每个 GPC 中包含 TPC（Texture processing cluster）表示纹理处理簇，每个处理簇被分为多个 SM（SMX、SMM，Streaming Multiprocessor 流式多处理器 是GPU的基础单元，隔壁AMD叫CU ）流处理器和一个光栅化引擎(Raster Engine)，SM 中包含多个 CUDA Core 和 Tensor Core，用于处理图形图形和 AI 张量计算。
  3. SM（Streaming Multiprocessors）称作流式多处理器，核心组件包括 CUDA 核心、共享内存、寄存器等。SM 包含很多为线程执行数学运算的 core，是英伟达 GPU 的核心，在 CUDA 中可以执行数百个线程、一个 block 上线程放在同一个 SM 上执行，一个 SM 有限的 Cache 制约了每个 block 的线程数量。

2.1 SM

程序员编写的shader代码是在SM上执行的。每个SM包含许多为线程执行数学运算的Core。一个线程对应一个Core，同时一个线程可以被shader代码调用进行运算。这些Core和其它部件由Warp Scheduler驱动，Warp Scheduler管理一个由32个线程组成Warp（线程束），其通过将要执行的shader指令移交给Instruction Dispatch Units(指令调度单元)来驱动Core和其他部件。GPU有多少这些单元，不同的芯片不一样，总的来说，越贵的越多，性能也就越好。

上图为一个SM的构成图，从上到下依次是：

  • PolyMorph Engine：多边形引擎负责属性装配（attribute Setup）、顶点拉取(VertexFetch)、曲面细分、栅格化（这个模块可以理解专门处理顶点相关的东西）。
  • 指令缓存（Instruction Cache）
  • 2个Warp Schedulers：这个模块负责warp调度，一个warp由32个线程组成，warp调度器的指令通过Dispatch Units送到Core执行。
  • 指令调度单元(Dispatch Units) 负责将Warp Schedulers的指令送往Core执行
  • 128KB Register File（寄存器）
  • 16个LD/ST（load/store）用来加载和存储数据
  • Core （Core，也叫流处理器Stream Processor）
  • 4个SFU（Special function units 特殊运算单元）执行特殊数学运算（sin、cos、log等）
  • 内部链接网络（Interconnect Network）
  • 64KB 共享缓存
  • 全局内存缓存（Uniform Cache）
  • 纹理读取单元(Tex)
  • 纹理缓存（Texture Cache）

SMM,SMX是之后对SM的升级，区别不是很大。SP（Streaming Processor）流处理器是最基本的处理单元，最后线程具体的指令和任务都是在 SP 上进行处理的，GPU 在进行并行计算时就是很多个 SP 同时处理。在 Fermi 架构之后，SP 被改称为 CUDA Core，通过 CUDA 来控制具体的指令执行。

GPU 工作原理

本章将从 GPU 硬件基础和英伟达 GPU 架构两个方面讲解 GPU 的工作原理。英伟达 GPU 有着很长的发展历史，整体架构从 Fermi 到 Blankwell 架构演变了非常多代，其中和 AI 特别相关的就有 Tensor Core 和 NVLink。

本节首先讲解 CPU 和 GPU 架构的区别，之后以$AX+Y$这个例子来探究 GPU 是如何做并行计算的，为了更好地了解 GPU 并行计算，对并发和并行这两个概念进行了区分。此外会讲解 GPU 的缓存机制，因为这将涉及到 GPU 的缓存（Cache）和线程（Thread）。

GPU 工作原理

基本工作原理

首先通过$AX+Y$这个加法运算的示例了解 GPU 的工作原理，$AX+Y$ 的示例代码如下：

  1.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="1">
class="hljs-ln-code"> class="hljs-ln-line">void demo(double alpha, double *x, double *y)
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="2">
    • class="hljs-ln-code"> class="hljs-ln-line">{
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="3"> class="hljs-ln-code"> class="hljs-ln-line"> int n = 2000;
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="4"> class="hljs-ln-code"> class="hljs-ln-line"> for (int i = 0; i < n; ++i)
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="5"> class="hljs-ln-code"> class="hljs-ln-line"> {
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="6"> class="hljs-ln-code"> class="hljs-ln-line"> y[i] = alpha * x[i] + y[i];
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="7"> class="hljs-ln-code"> class="hljs-ln-line"> }
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="8"> class="hljs-ln-code"> class="hljs-ln-line">}
    •  class="hljs-button signin active" data-title="登录复制" data-report-click="{"spm":"1001.2101.3001.4334"}" onclick="hljs.signin(event)">

    示例代码中包含 2 FLOPS 操作，分别是乘法（Multiply）和加法（Add），对于每一次计算操作都需要在内存中读取两个数据，$x[i]$ 和 $y[i]$，最后执行一个线性操作，存储到 $y[i]$ 中，其中把加法和乘法融合在一起的操作也可以称作 FMA（Fused Multiply and Add）。

    在 O(n) 的时间复杂度下，根据 n 的大小迭代计算 n 次，在 CPU 中串行地按指令顺序去执行 $AX+Y$ 程序。以 Intel Exon 8280 这款芯片为例，其内存带宽是 131 GB/s，内存的延时是 89 ns，这意味着 8280 芯片的峰值算力是在 89 ns 的时间内传输 11659 个比特（byte）数据。$AX+Y$ 将在 89 ns 的时间内传输 16 比特（C/C++中 double 数据类型所占的内存空间是 8 bytes）数据，此时内存的利用率只有 0.14%（16/11659），存储总线有 99.86% 的时间处于空闲状态。

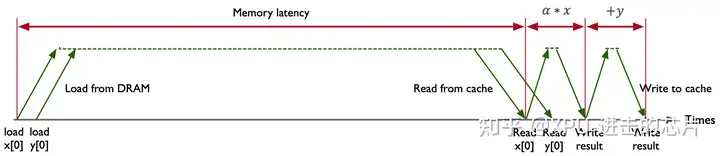
    内存总线 99.86%时间处于空闲状态

    不同处理器计算 $AX+Y$ 时的内存利用率，不管是 AMD Rome 7742、Intel Xeon 8280 还是 NVIDIA A100，对于 $AX+Y$ 这段程序的内存利用率都非常低，基本 ≤0.14%。

    class="table-box">
    AMD Rome 7742Intel Xeon 8280NVIDIA A100
    Memory B/W(GB/sec)2041311555
    DRAM Latency(ns)12289404
    Peak bytes per latency24,88811,659628,220
    Memory Efficiency0.064%0.14%0.0025%

    由于上面的 $AX+Y$ 程序没有充分利用并发和线性度，因此通过并发进行循环展开的代码如下：

    1.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="1"> class="hljs-ln-code"> class="hljs-ln-line">void fun_axy(int n, double alpha, double *x, double *y)
    2.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="2"> class="hljs-ln-code"> class="hljs-ln-line">{
    3.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="3"> class="hljs-ln-code"> class="hljs-ln-line">    for (int i = 0; i < n; i += 8)
    4.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="4"> class="hljs-ln-code"> class="hljs-ln-line">    {
    5.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="5"> class="hljs-ln-code"> class="hljs-ln-line">        y[i + 0] = alpha * x[i + 0] + y[i + 0];
    6.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="6"> class="hljs-ln-code"> class="hljs-ln-line">        y[i + 1] = alpha * x[i + 1] + y[i + 1];
    7.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="7"> class="hljs-ln-code"> class="hljs-ln-line">        y[i + 2] = alpha * x[i + 2] + y[i + 2];
    8.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="8"> class="hljs-ln-code"> class="hljs-ln-line">        y[i + 3] = alpha * x[i + 3] + y[i + 3];
    9.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="9"> class="hljs-ln-code"> class="hljs-ln-line">        y[i + 4] = alpha * x[i + 4] + y[i + 4];
    10.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="10"> class="hljs-ln-code"> class="hljs-ln-line">        y[i + 5] = alpha * x[i + 5] + y[i + 5];
    11.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="11"> class="hljs-ln-code"> class="hljs-ln-line">        y[i + 6] = alpha * x[i + 6] + y[i + 6];
    12.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="12"> class="hljs-ln-code"> class="hljs-ln-line">        y[i + 7] = alpha * x[i + 7] + y[i + 7];
    13.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="13"> class="hljs-ln-code"> class="hljs-ln-line">    }
    14.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="14"> class="hljs-ln-code"> class="hljs-ln-line">}
     class="hljs-button signin active" data-title="登录复制" data-report-click="{"spm":"1001.2101.3001.4334"}" onclick="hljs.signin(event)">

    每次执行从 0 到 7 的数据，实现一次性迭代 8 次，每次传输 16 bytes 数据，因此同样在 Intel Exon 8280 芯片上，每 89 ns 的时间内将执行 729（11659/16）次请求，将程序这样改进就是通过并发使整个总线处于一个忙碌的状态，但是在真正的应用场景中：

    由此可以看出，虽然并发的操作能够一次性执行更多的指令流水线操作，但是同样架构也会受到限制和约束。

    将 $Z=AX+Y$ 通过并行进行展开，示例代码如下：

    1.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="1"> class="hljs-ln-code"> class="hljs-ln-line">void fun_axy(int n, double alpha, double *x, double *y)
    2.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="2"> class="hljs-ln-code"> class="hljs-ln-line">{
    3.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="3"> class="hljs-ln-code"> class="hljs-ln-line">    Parallel for (int i = 0; i < n; i++)
    4.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="4"> class="hljs-ln-code"> class="hljs-ln-line">    {
    5.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="5"> class="hljs-ln-code"> class="hljs-ln-line">        y[i] = alpha * x[i] + y[i];
    6.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="6"> class="hljs-ln-code"> class="hljs-ln-line">    }
    7.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="7"> class="hljs-ln-code"> class="hljs-ln-line">}
     class="hljs-button signin active" data-title="登录复制" data-report-click="{"spm":"1001.2101.3001.4334"}" onclick="hljs.signin(event)">

    通过并行的方式进行循环展开，并行就是通过并行处理器或者多个线程去执行 $AX+Y$ 这个操作，同样使得总线处于忙碌的状态，每一次可以执行 729 个迭代。相比较并发的方式：

    GPU 线程原理

    GPU 整体架构和单个 SM（Streaming Multiprocessor）的架构，SM 可以看作是一个基本的运算单元，GPU 在一个时钟周期内可以执行多个 Warp，在一个 SM 里面有 64 个 Warp，其中每四个 Warp 可以单独进行并发的执行，GPU 的设计者主要是增加线程和增加 Warp 来解决或者掩盖延迟的问题，而不是去减少延迟的时间。

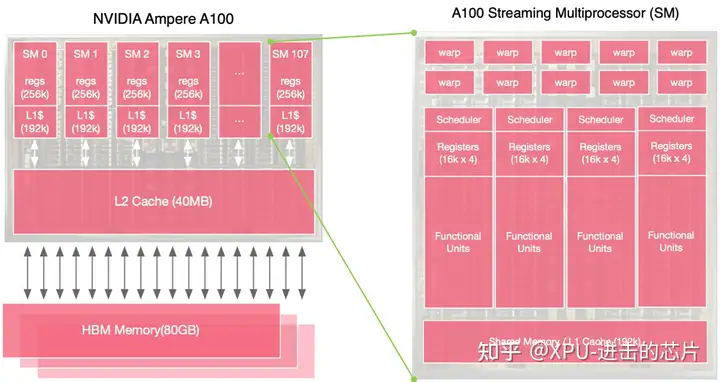
    GPU 整体架构与 SM 架构

    为了有更多的线程处理计算任务，GPU SMs 线程会选择超配，每个 SM 一共有 2048 个线程，整个 A100 有 20 多万个线程可以提供给程序，在实际场景中程序用不完所有线程，因此有一些线程处于计算的过程中，有一些线程负责搬运数据，还有一些线程在同步地等待下一次被计算。很多时候会看到 GPU 的算力利用率并不是非常的高，但是完全不觉得它慢是因为线程是超配的，远远超出大部分应用程序的使用范围，线程可以在不同的 Warp 上面进行调度。

    class="table-box">
    Pre SMA100
    Total Threads2048221,184
    Total Warps646,912
    Active Warps4432
    Waiting Warps606,480
    Active Threads12813,824
    Waiting Threads1,920207,360

    小结

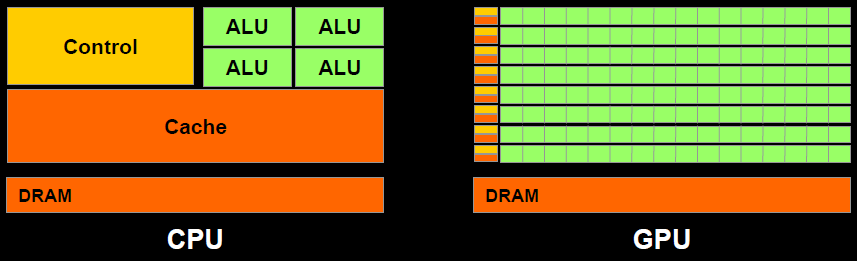
    本节首先从架构层面分析了 CPU 和 GPU 的主要区别，因为 CPU 的设计目标是尽可能在低的延迟下执行任务，GPU 的设计目标是最大化吞吐量，因此决定了 CPU 适合处理顺序执行的任务，GPU 适合处理大规模并行计算的任务。

    以 $AX+Y$ 为例讲解了并发和并行的区别以及和串行的区别，在串行计算时内存利用率很低，当把程序用并发的方式展开，并发操作的多流水线会受到 CPU 架构的限制，当程序用并行的方式循环展开时，程序的执行则只受到线程数量和内存请求的约束，因此 CPU 跟 GPU 的本质区别是并行的问题而不是并发的问题，GPU 通过大量的线程提供并行的能力。

    为了提供并行的能力，GPU 通过多级缓存、多级流水、多级 Cache 提供并行的机制，同时可以尽可能减少内存的时延。为了将数据充分利用起来，引入了 GPU 线程的原理，GPU 里面提供了大量超配的线程去完成对不同层级数据的搬运和计算。

    2.2 Computational  Units (cores)

    总的来看，我们可以这样说：CPU的Computational units是“大”而“少”的，然而GPU的Computational units是“小”而“多”的，这里的大小是指的计算能力，多少指的是设备中的数量。通过观察上图，显然可以看出，绿色的部分，CPU“大少”，GPU“小多”的特点。

    CPU的cores 比GPU的cores要更加聪明(smarter)，这也是所谓“大”的特点。

    在过去的很长时间里，CPU的core计算能力增长是得益于主频时钟最大的频率增长。相反，GPU不仅没有主频时钟的提升，而且还经历过主频下降的情况，因为GPU需要适应嵌入式应用环境，在这个环境下对功耗的要求是比较高的，不能容忍超高主频的存在。例如英伟达的Jetson NANO,安装在室内导航机器人身上，就是一个很好的嵌入式环境应用示例，安装在机器人身上，就意味着使用电池供电，GPU的功耗不可以过高。(see,Indoor Mapping and Navigation Robot Build with ROS and Nvidia Jetson Nano):

    CPU比GPU聪明，很大一个原因就是CPU拥有"out-of-order exectutions"（乱序执行）功能。出于优化的目的，CPU可以用不同于输入指令的顺序执行指令，当遇到分支的时候，它可以预测在不久的将来哪一个指令最有可能被执行到（multiple branch prediction 多重分支预测）。通过这种方式，它可以预先准备好操作数，并且提前执行他们（soeculative execution 预测执行），通过上述的几种方式节省了程序运行时间。

    显然现代CPU拥有如此多的提升性能的机制，这是比GPU聪明的地方。

    相比之下，GPU的core不能做任何类似out-of-order exectutions那样复杂的事情，总的来说，GPU的core只能做一些最简单的浮点运算,例如 multiply-add(MAD)或者 fused multiply-add(FMA)指令

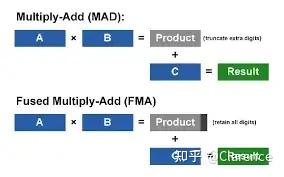
    通过上图可以看出MAD指令实际是计算A*B+C的值。

    实际上，现代GPU结构，CORE不仅仅可以结算FMA这样简单的运算，还可以执行更加复杂的运算操作，例如tensor张量(tensor core)或者光线追踪(ray tracing core)相关的操作。

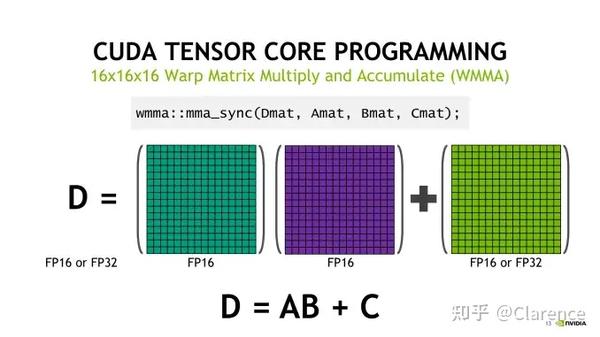
    张量计算tensor core

    光线追踪

    张量核心(tensor cores)的目的在于服务张量操作在一些人工智能运算场合，光纤追踪（ray tracing） 旨在服务超现实主义（hyper-realistic）实时渲染的场合。

    上文说到，GPU Core最开始只是支持一些简单的浮点运算FMA,后来经过发展又增加了一些复杂运算的机制tensor core以及ray trace，但是总体来说GPU的计算灵活性还是比不上CPU的核心。

    值得一提的是，GPU的编程方式是SIMD(Single Instruction Multiple Data)意味着所有Core的计算操作完全是在相同的时间内进行的，但是输入的数据有所不同。显然，GPU的优势不在于核心的处理能力，而是在于他可以大规模并行处理数据。

    赛艇运动中，所有人同时齐心划船

    GPU中每个核心的作用有点像罗马帆船上的桨手：鼓手打着节拍（时钟），桨手跟着节拍一同滑动帆船。

    SIMD编程模型允许加速运行非常多的应用，对图像进行缩放就是一个很好的例子。在这个例子中，每个core对应图像的一个像素点，这样就可以并行的处理每一个像素点的缩放操作，如果这个工作给到CPU来做，需要N的时间才可以做完，但是给到GPU只需要一个时钟周期就可以完成，当然，这样做的前提是有足够的core来覆盖所有的图像像素点。这个问题有个显著的特点，就是对一张图像进行缩放操作，各个像素点之间的信息是相互独立的，因此可以独立的放在不同的core中进行并行运算。我们认为不同的core操作的信息相互独立，是符合SIMD的模型的，使用SIMD来解决这样的问题非常方便。

    但是，也不是所有的问题都是符合SIMD模型的，尤其在异步问题中，在这样的问题中，不同的core之间要相互交互信息，计算的结构不规则，负载不均衡，这样的问题交给GPU来处理就会比较复杂。

    2.2. GPU多核底层结构

    为了充分理解GPU的架构，让我们在返回来看下第一张图，一个显卡中绝大多数都是计算核心core组成的海洋。

    在图像缩放的例子中，core与core之间不需要任何协作，因为他们的任务是完全独立的，然而，GPU解决的问题不一定这么简单，让我们来举个例子。

    假设我们需要对一个数组里的数进行求和，这样的运算属于reductuin family类型，因为这样的运算试图将一个序列“reduce”简化为一个数。计算数组的元素总和的操作看起来是顺序的，我们只需要获取第一个元素，求和到第二个元素中，获取结果，再将结果求和到第三个元素，以此类推。

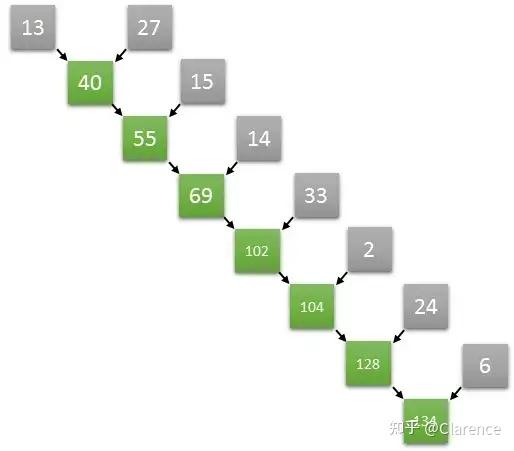
    Sequential reduction

    令人惊讶的是，一些看起来本质是顺序的运算，其实可以再并行算法中转化。假设一个长度为8的数组，在第一步中完全可以并行执行两个元素和两个元素的求和，从而同时获得四个元素，两两相加的结果，以此类推，通过并行的方式加速数组求和的运算速度。具体的操作如下图所示，

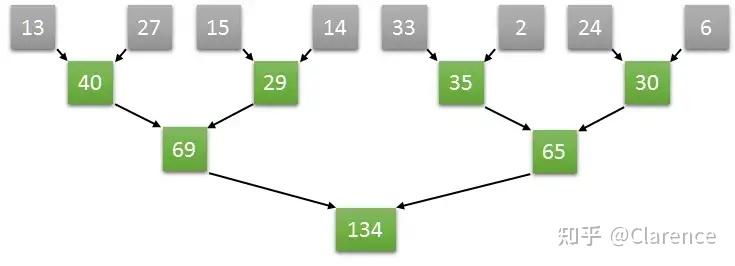
    Parallel reduction

    如上图计算方式，如果是长度为8的数组两两并行求和计算，那么只需要三次就可以计算出结果。如果是顺序计算需要8次。如果按照两两并行相加的算法，N个数字相加，那么仅需要log2（N）次就可以完成计算。

    从GPU的角度来讲，只需要四个core就可以完成长度为8的数组求和算法，我们将四个core编号为0，1，2，3。

    那么第一个时钟下，两两相加的结果通过0号core计算，放入了0号core可以访问到的内存中，另外两两对分别由1号2号3号core来计算，第二个个时钟继续按照之前的算法计算，只需要0号和1号两个core即可完成，以此类推，最终的结果将在第三个时钟由0号core计算完成，并储存在0号core可以访问到的内存中。这样实际三次就能完成长度为8的数组求和计算。

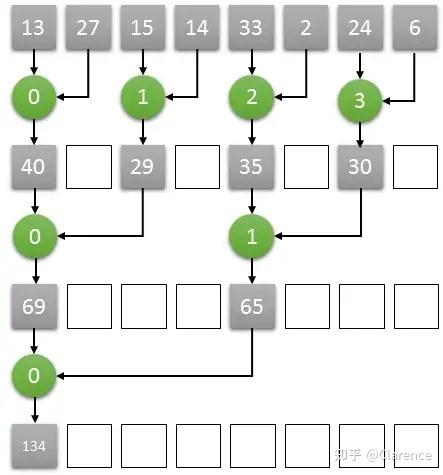
    Parallel reduction with a GPU

    如果GPU想要完成上述的推理计算过程，显然，多个core之间要可以共享一段内存空间以此来完成数据之间的交互，需要多个core可以在共享的内存空间中完成读/写的操作。我们希望每个Cores都有交互数据的能力，但是不幸的是，一个GPU里面可以包含数以千计的core，如果使得这些core都可以访问共享的内存段是非常困难和昂贵的。出于成本的考虑，折中的解决方案是将各类GPU的core分类为多个组，形成多个流处理器(Streaming Multiprocessors )或者简称为SMs。

     The Turing SM

    在SM的图灵结构中，绿色的部分CORE相关的，我们进一步区分了不同类型的CORE。主要分为INT32,FP32，TENSOR CORES。

    FP32 Cores，执行单进度浮点运算，在TU102卡中，每个SM由64个FP32核，TU120由72个SMs因此，FP32 Core的数量是 72 * 64。

    FP64 Cores. 实际上每个SM都包含了2个64位浮点计算核心FP64 Cores，用来计算双精度浮点运算，虽然上图没有画出，但是实际是存在的。

    Integer Cores，这些core执行一些对整数的操作，例如地址计算，可以和浮点运算同时执行指令。在前几代GPU中，执行这些整型操作指令都会使得浮点运算的管道停止工作。TU102总共由4608个Integer Cores，每个SM有64个SM。

    Tensor Cores，张量core是FP16单元的变种，认为是半精度单元，致力于张量积算加速常见的深度学习操作。图灵张量Core还可以执行INT8和INT4精度的操作，用于可以接受量化而且不需要FP16精度的应用场景，在TU102中，我们每个SM有8个张量Cores，一共有8 * 72个Tensor Cores。

    在大致描述了GPU的执行部分之后，让我们回到上文提出的问题，各个核心之间如何完成彼此的协作？

    在四个SM块的底部有一个96KB的L1 Cache，用浅蓝色标注的。这个cache段是允许各个Core都可以访问的段，在L1 Cache中每个SM都有一块专用的共享内存。作为芯片上的L1 cache他的大小是有限的，但它非常快，肯定比访问GMEM快得多。

    实际上L1 CACHE拥有两个功能，一个是用于SM上Core之间相互共享内存，另一个则是普通的cache功能。当Core需要协同工作，并且彼此交换结果的时候，编译器编译后的指令会将部分结果储存在共享内存中，以便于不同的core获取到对应数据。当用做普通cache功能的时候，当core需要访问GMEM数据的时候，首先会在L1中查找，如果没找到，则回去L2 cache中寻找，如果L2 cache也没有，则会从GMEM中获取数据，L1访问最快 L2 以及GMEM递减。缓存中的数据将会持续存在，除非出现新的数据做替换。从这个角度来看，如果Core需要从GMEM中多次访问数据，那么编程者应该将这块数据放入功能内存中，以加快他们的获取速度。其实可以将共享内存理解为一段受控制的cache，事实上L1 cache和共享内存是同一块电路中实现的。编程者有权决定L1 的内存多少是用作cache多少是用作共享内存。

    最后，也是比较重要的是，可以储存各个core的计算中间结果，用于各个核心之间共享的内存段不仅仅可以是共享内存L1，也可以是寄存器，寄存器是离core最近的内存段，但是也非常小。最底层的思想是每个线程都可以拥有一个寄存器来储存中间结果，每个寄存器只能由相同的一个线程来访问，或者由相同的warp或者组的线程访问。

    小结

    这篇文章，主要阐述了GPU的基本底层构成，主要是以TU120来举例，讲解了GPU计算核心 Cores,以及Memory以及控制单元，三大组成要素。Core是计算的基本单元，既可以用作简单的浮点运算，又可以做一些复杂的运算例如，tensor 或者ray tracing。文中谈到了多个core之间通讯的方式，在特定的应用场合多个core之间是不需要的通讯的，也就是各干各的（例如 图像缩放），但是也有一些例子，多个core之间要相互通讯配合（例如上文谈到的数组求和问题），每个core之间都可以实现交互数据是非常昂贵的，因此提出了SMs的概念，SMs是多个core的集合，一个SMs里面的cores可以通过L1 Cache进行交互信息，完成使用GPU处理数组求和问题的时候，多个核心共享数据的功能。

    关于memory，文章谈到，存在全局的内存GMEM，但是访问较慢，Cores当需要访问GMEM的时候会首先访问L1,L2如果都miss了，那么才会花费大代价到GMEM中寻找数据。

    读了这篇来自Vitality Learning的文章，我对GPU的底层硬件结构有了初步认识，收益颇丰！

    2.3. memory

    回到这个文章的第一张图中来，我们接下来会讨论GPU和CPU内存方面的差别。

    CPU的memory系统一般是基于DRAM的，在桌面PC中，一般来说是8G，在服务器中能达到数百（256）Gbyte。

    CPU内存系统中有个重要的概念就是cache，是用来减少CPU访问DRAM的时间。cache是一片小，但是访问速度更快，更加靠近处理器核心的内存段，用来储存DRAM中的数据副本。cache一般有一个分级，通常分为三个级别L1，L2，L3 cache，cache离核心越近就越小访问越快，例如 L1可以是64KB L2就是256KB L3是4MB。

    CPU Cache的内容不再这里展开讲解，感兴趣的读者可以自行查阅资料。

    从第一张图可以看到GPU中有一大片橙色的内存，名称为DRAM，这一块被称为全局内存或者GMEM。GMEM的内存大小要比CPU的DRAM小的多，在最便宜的显卡中一般只有几个G的大小，在最好的显卡中GMEM可以达到24G。GMEM的尺寸大小是科学计算使用中的主要限制。十年前，显卡的容量最多也就只有512M,但是，现在已经完全克服了这个问题。

    关于cache，从第一张图中不难推断，左上角的小橙色块就是GPU的cache段。然而GPU的缓存机制和CPU是存在一定的差异的，稍后将会证明这一点。

    GPU 缓存机制

    在 GPU 工作过程中希望尽可能的去减少内存的时延、内存的搬运、还有内存的带宽等一系列内存相关的问题，其中缓存对于内存尤为重要。NVIDIA Ampere A100 内存结构中 HBM Memory 的大小是 80G，也就是 A100 的显存大小是 80G。

    其中寄存器（Register）文件也可以视为缓存，寄存器靠近 SM（Streaming Multiprocessors）执行单元，从而可以快速地获取执行单元中的数据，同时也方便读取 L1 Cache 缓存中的数据。此外 L2 Cache 更靠近 HBM Memory，这样方便 GPU 把大量的数据直接搬运到 cache 中，因此为了同时实现上面两个目标， GPU 设计了多级缓存。80G 的显存是一个高带宽的内存，L2 Cache 大小为 40M，所有 SM 共享同一个 L2 Cache，L1 Cache 大小为 192kB，每个 SM 拥有自己独立的 Cache，同样每个 SM 拥有自己独立的 Register，每个寄存器大小为 256 kB，因为总共有 108 个 SM 流处理器，因此寄存器总共的大小是 27MB，L1 Cache 总共的大小是 20 MB。

    NVIDIA Ampere A100 内存结构

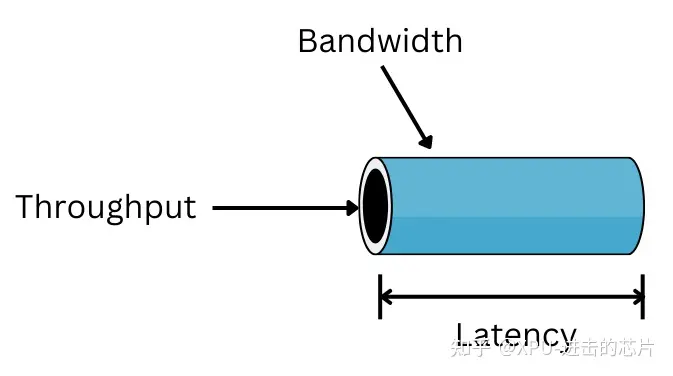
    GPU 和 CPU 内存带宽和时延进行比较，在 GPU 中如果把主内存（HBM Memory）作为内存带宽（B/W, bandwidth）的基本单位，L2 缓存的带宽是主内存的 3 倍，L1 缓存的带宽是主存的 13 倍。在真正计算的时候，希望缓存的数据能够尽快的去用完，然后读取下一批数据，此时时候就会遇到时延（Lentency）的问题。如果将 L1 缓存的延迟作为基本单位，L2 缓存的延迟是 L1 的 5 倍，HBM 的延迟将是 L1 的 15 倍，因此 GPU 需要有单独的显存。

    假设使用 CPU 将 DRAM（Dynamic Random Access Memory）中的数据传入到 GPU 中进行计算，较高的时延（25 倍）会导致数据传输的速度远小于计算的速度，因此需要 GPU 有自己的高带宽内存 HBM（High Bandwidth Memory），GPU 和 CPU 之间的通信和数据传输主要通过 PCIe 来进行。

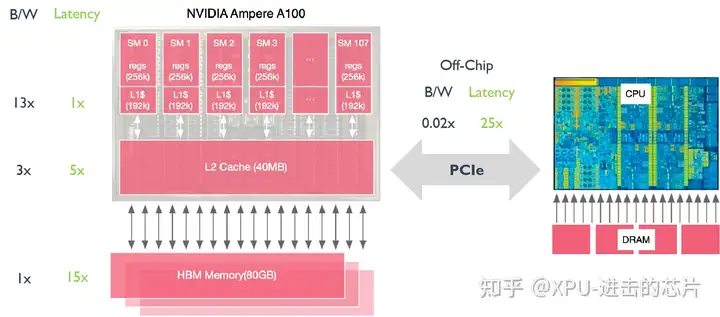
    NVIDIA Ampere A100 存储延迟对比

    DRAM 动态 随机存取存储器（Dynamic Random Access Memory）
    一种计算机内存类型，用于临时存储计算机程序和数据，以供中央处理器（CPU）快速访问。与静态随机存取存储器（SRAM）相比，具有较高的存储密度和较低的成本，但速度较慢。它是计算机系统中最常用的内存类型之一，用于存储操作系统、应用程序和用户数据等内容。
    DRAM 的每个存储单元由一个电容和一个晶体管组成，电容负责存储数据位（0 或 1），晶体管用于读取和刷新数据。由于电容会逐渐失去电荷，因此需要定期刷新（称为刷新操作）以保持数据的正确性，这也是称为“动态”的原因，用于临时存储数据和程序，提供快速访问速度和相对较低的成本。
    class="table-box">
    存储类型结构工作原理性能应用
    DRAM（Dynamic Random Access Memory）一种基本的内存技术，通常以单层平面的方式组织，存储芯片分布在一个平面上当读取数据时，电荷被传递到输出线路，然后被刷新。当写入数据时，电荷被存储在电容中。由于电容会逐渐失去电荷，因此需要周期性刷新来保持数据具有较高的密度和相对较低的成本，但带宽和延迟相对较高常用于个人电脑、笔记本电脑和普通服务器等一般计算设备中
    GDDR（Graphics Double Data Rate）专门为图形处理器设计的内存技术，具有较高的带宽和性能在数据传输速度和带宽方面优于传统的 DRAM，适用于图形渲染和视频处理等需要大量数据传输的应用GDDR 与标准 DDR SDRAM 类似，但在设计上进行了优化以提供更高的数据传输速度。它采用双倍数据速率传输，即在每个时钟周期传输两次数据，提高了数据传输效率主要用于高性能图形处理器（GPU）和游戏主机等需要高带宽内存的设备中
    HBM（High Bandwidth Memory）使用堆叠设计，将多个 DRAM 存储芯片堆叠在一起，形成三维结构堆叠设计允许更短的数据传输路径和更高的带宽，同时减少了功耗和延迟。每个存储芯片通过硅间连接（Through Silicon Via，TSV）与其他存储芯片通信，实现高效的数据传输具有非常高的带宽和较低的延迟，适用于高性能计算和人工智能等需要大量数据传输的领域主要用于高端图形处理器（GPU）、高性能计算系统和服务器等需要高带宽内存的设备中

    不同存储和传输的带宽和计算强度进行比较，假设 HBM 计算强度为 100，L2 缓存的计算强度只为 39，意味着每个数据只需要执行 39 个操作，L1 的缓存更少，计算强度只需要 8 个操作，这个时候对于硬件来说非常容易实现。这就是为什么 L1 缓存、L2 缓存和寄存器对 GPU 来说如此重要。可以把数据放在 L1 缓存里面然后对数据进行 8 个操作，使得计算达到饱和的状态，使 GPU 里面 SM 的算力利用率更高。但是 PCIe 的带宽很低，整体的时延很高，这将导致整体的算力强度很高，算力利用率很低。

    class="table-box">
    DataLocationBandwidth(GB/sec)ComputeIntensityLatency(ns)Threads Required
    L1 Cache19,40082732,738
    L2 Cache4,0003915037,500
    HBM1,55510040439,264
    NVLink30052070013,125
    PCIe25624014702297

    在带宽增加的同时线程的数量或者线程的请求数也需要相对应的增加，这个时候才能够处理并行的操作，每个线程执行一个对应的数据才能够把算力利用率提升上去，只有线程数足够多才能够让整个系统的内存处于忙碌的状态，让计算也处于忙碌的状态，因此看到 GPU 里面的线程数非常多。

    3. GPU 逻辑管线介绍

    因为GPU是为了图形处理而诞生的，所以想要整明白GPU的架构，首先也要对渲染管线有一定的了解，下面是DirectX的渲染管线流程图，递归这看懂了然后我们继续：

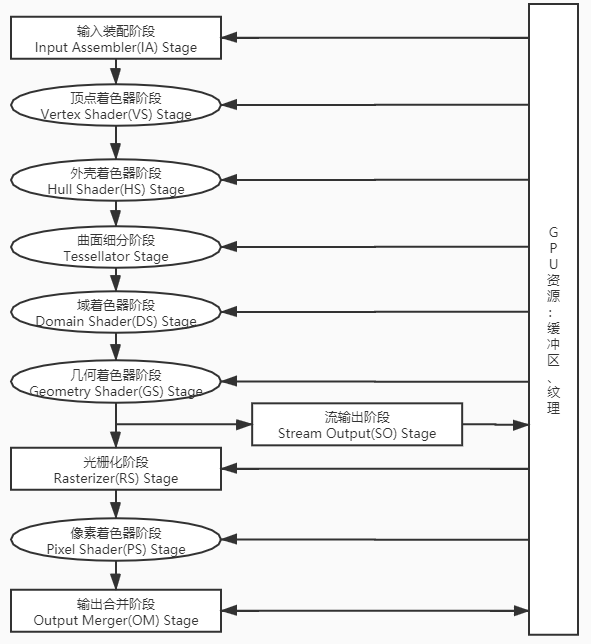
    为了简单起见，我们做一些假设。我们假设已经填充了数据并存在于 GPU 的 DRAM 中，并且在整个流程中仅使用VS和PS。

    GPU图形处理，可以大致分成 5 个步骤，如下图箭头的部分。

    分别为 vertex shader、primitive processing、rasterisation、fragment shader、testing and blending。

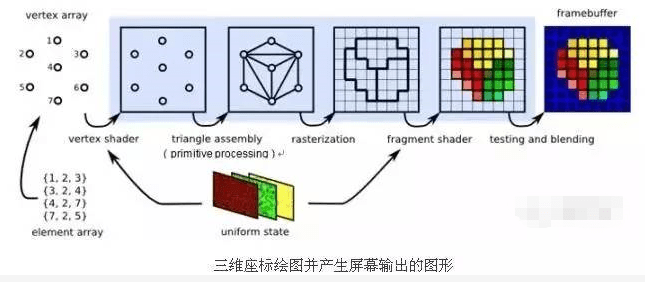
    第一步，vertex shader。是将三维空间中数个（x,y,z）顶点放进 GPU 中。

    在这一步骤中，电脑会在内部模拟出一个三维空间，并将这些顶点放置在这一空间内部。接着，投影在同一平面上，也是我们将看到的画面。同时，存下各点距离投影面的垂直距离，以便做后续的处理。

    这个过程就像是本地球观看星星一般。地球的天空，就像是一个投影面，所有的星星，不管远近皆投影在同一面上。本地球的我们，抬起头来观看星星，分不出星星的远近，只能分辨出亮度。

    GPU 所投影出的结果，和这个情况类似。

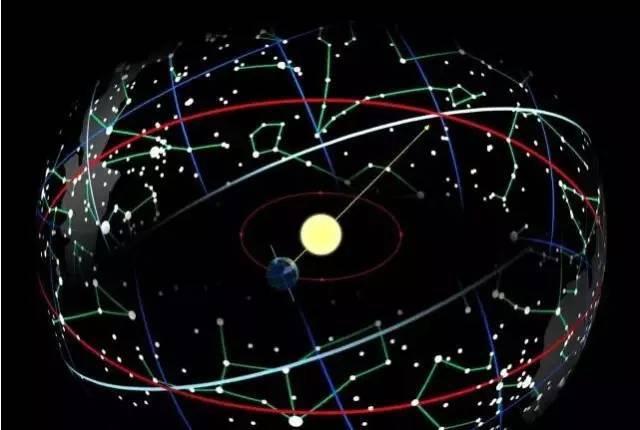
    从地球所看到的星空，星星就像是投影到一球面上，除非使用特别的仪器，不然分不出星星和地球的距离

    第二步，primitive processing。是将相关的点链接在一起，以形成图形。在一开始输入数个顶点进入 GPU 时，程序会特别注记哪些点是需要组合在一起，以形成一线或面。就像是看星座的时候一样，将相关连的星星连起来，形成特定的图案。

    第三步，rasterisation。因为电脑的屏幕是由一个又一个的像素组成，因此，需要将一条连续的直线，使用绘图的演算法，以方格绘出该直线。图形也是以此方式，先标出边线，再用方格填满整个平面。

    第四步，fragment shader。将格点化后的图形着上颜色。所需着上的颜色也是于输入时便被注记。在游玩游戏时，这一步相当耗费 GPU 的计算资源，因为光影的效果、物体表面材质皆是在这一步进行，这些计算决定着游戏画面的精细程度。因此在游玩游戏时，调高游戏画面品质大幅增加这一步的计算负担，降低游戏品质。

    将一个三角形，用方格呈现近似原始图案，并着上颜色。一块又一块的方格，就是显示器上的像素

    最后一步，testing and blending。便是将第一步所获得的投影垂直距离取出，和第四步的结果一同做最后处理。在去除被会被其他较近距离的物体挡住的物体后，让剩下的图形放进 GPU 的输出内存。之后，结果便会被送到电脑屏幕显示。

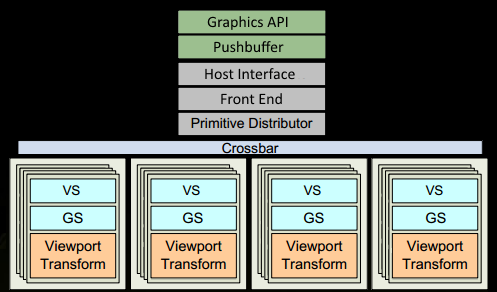
    1. 程序在图形 API(DirectX 或 openGL）中进行绘图调用（drawcall）。在这里对数据进行合法性检查后，数据会被GPU可读编码后插入到Pushbuffer中。在这个过程中在 CPU 方面可能会出现很多瓶颈，这也是我们常说的DrawCall瓶颈的问题所在。
    2. 一段时间后或者显式刷新（explicit "flush" calls）后，驱动程序已在pushbuffer 中缓冲了足够的work并将其发送给 GPU 进行处理（在操作系统的某些参与下）。GPU 的Host Interface接收通过Front End处理。
    3. 数据完全到达GPU后，在图元分配器(Primitive Distributor)中开始工作分配，处理indexbuffer，将处理得到的三角形分成batch，发送给多个GPC。

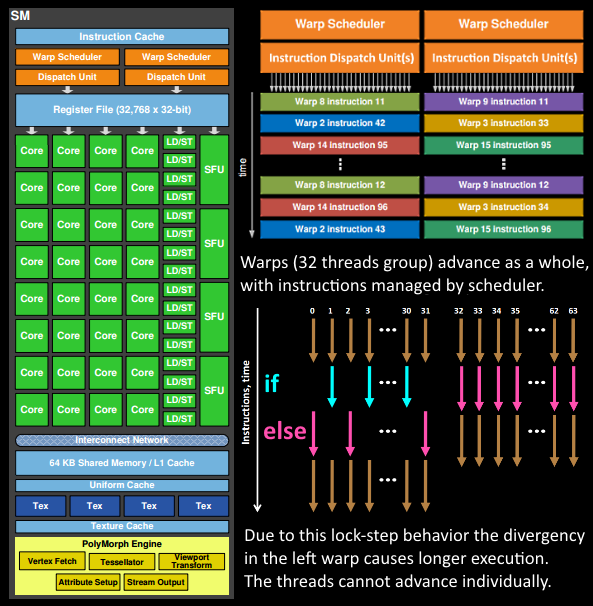
    1. 在GPC中，每个SM中的Poly Morph Engine负责通过三角形索引(triangle indices)取出三角形的数据(vertex data)，即下图中的Vertex Fetch模块。
    2. 在获取数据之后，在SM中以32个线程为一组的线程束(Warp)来调度，来开始处理顶点数据。
    3. SM的warp调度器会按照顺序分发指令给整个warp，单个warp中的线程会锁步(lock-step)执行各自的指令，如果线程碰到不激活执行的情况也会被遮掩(be masked out)。被遮掩的原因有很多，例如当前的指令是if(true)的分支，但是当前线程的数据的条件是false，或者循环的次数不一样（比如for循环次数n不是常量，或被break提前终止了但是别的还在走），因此在shader中的分支会显著增加时间消耗，在一个warp中的分支除非32个线程都走到if或者else里面，否则相当于所有的分支都走了一遍，线程不能独立执行指令而是以warp为单位，而这些warp之间才是独立的。
    4. warp中的指令可以被一次完成，也可能经过多次调度，例如通常SM中的LD/ST(加载存取)单元数量明显少于基础数学操作单元。
    5. 由于某些指令比其他指令需要更长的时间才能完成，特别是内存加载，warp调度器可能会简单地切换到另一个没有内存等待的warp，这是GPU如何克服内存读取延迟的关键，只是简单地切换活动线程组。为了使这种切换非常快，调度器管理的所有warp在寄存器文件中都有自己的寄存器。这里就会有个矛盾产生，shader需要越多的寄存器，就会给warp留下越少的空间，就会产生越少的warp，这时候在碰到内存延迟的时候就会只是等待，而没有可以运行的warp可以切换。

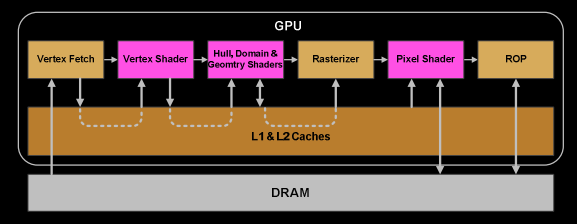
    1. 一旦warp完成了vertex-shader的所有指令，运算结果会被Viewport Transform模块处理，三角形会被裁剪然后准备栅格化，GPU会使用L1和L2缓存来进行vertex-shader和pixel-shader的数据通信。
    2. 接下来这些三角形将被分割，再分配给多个GPC，三角形的范围决定着它将被分配到哪个光栅引擎(raster engines)，每个raster engines覆盖了多个屏幕上的tile，这等于把三角形的渲染分配到多个tile上面。也就是像素阶段就把按三角形划分变成了按显示的像素划分了。
    3. SM上的Attribute Setup保证了从vertex-shader来的数据经过插值后是pixel-shade是可读的。
    4. GPC上的光栅引擎(raster engines)在它接收到的三角形上工作，来负责这些这些三角形的像素信息的生成（同时会处理裁剪Clipping、背面剔除和Early-Z剔除）。
    5. 32个像素线程将被分成一组，或者说8个2x2的像素块，这是在像素着色器上面的最小工作单元，在这个像素线程内，如果没有被三角形覆盖就会被遮掩，SM中的warp调度器会管理像素着色器的任务。
    6. 接下来的阶段就和vertex-shader中的逻辑步骤完全一样，但是变成了在像素着色器线程中执行。 由于不耗费任何性能可以获取一个像素内的值，导致锁步执行非常便利，所有的线程可以保证所有的指令可以在同一点。

    1. 最后一步，现在像素着色器已经完成了颜色的计算还有深度值的计算，在这个点上，我们必须考虑三角形的原始api顺序，然后才将数据移交给ROP(render output unit，渲染输入单元)，一个ROP内部有很多ROP单元，在ROP单元中处理深度测试，和framebuffer的混合，深度和颜色的设置必须是原子操作，否则两个不同的三角形在同一个像素点就会有冲突和错误。

    流程结束。

    这个时候我们再来回顾一下这张图：

    这会儿就会比较清晰了。

    参考

    1. ^life-triangle Life of a triangle - NVIDIA's logical pipeline | NVIDIA Developer
    2. ^X-Jun的DX11教程 https://www.cnblogs.com/X-Jun/p/9028764.html#_lab2_8_2

    作者：Clarence
    链接：https://zhuanlan.zhihu.com/p/598173226
     

    原文地址 ：Understanding the architecture of a GPU | by Vitality Learning | CodeX | Medium

    Author ：Vitality Learning

    作者：XPU-进击的芯片
    链接：https://www.zhihu.com/question/559866344/answer/3498127927
    来源：知乎
    著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
     

    作者：渲大师
    链接：https://zhuanlan.zhihu.com/p/530141476
    来源：知乎
    著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
     

    参考资料

    data-report-view="{"mod":"1585297308_001","spm":"1001.2101.3001.6548","dest":"https://blog.csdn.net/u012294613/article/details/140209282","extend1":"pc","ab":"new"}">>
    注：本文转载自blog.csdn.net的生活需要深度的文章"https://blog.csdn.net/u012294613/article/details/140209282"。版权归原作者所有，此博客不拥有其著作权，亦不承担相应法律责任。如有侵权，请联系我们删除。
    复制链接
    复制链接
    相关推荐
    发表评论

    评论记录：

    未查询到任何数据！