作者 |  channingbreeze
责编 | 郭芮

小史是一个应届生，虽然学的是电子专业，但是自己业余时间看了很多互联网与编程方面的书，一心想进BAT互联网公司。

今天小史去了一家社交小巨头公司面试了。

面试现场

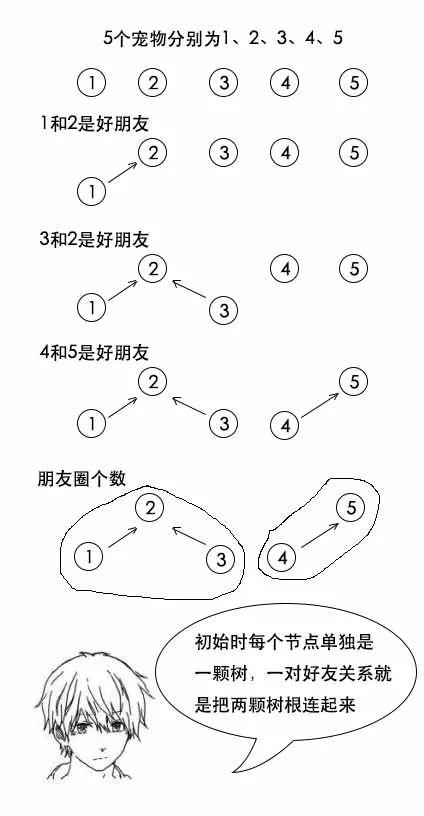
面试官：举个例子，比如现在有5个宠物，分别是小猫1，小猫2，小猫3，小狗1，小狗2。再告诉你小猫1和小狗1是好朋友，小猫2和小狗1是好朋友，小猫3和小狗2是好朋友。这样它们之间就形成了2个朋友圈。

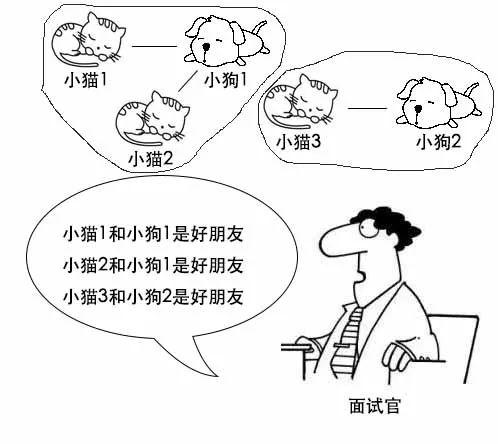
小史：先对宠物们编号，然后一对好友关系就用一个bitmap来存。判断两个bitmap之间是否有交集，只需要进行与操作。而融合的话只需要进行并操作。

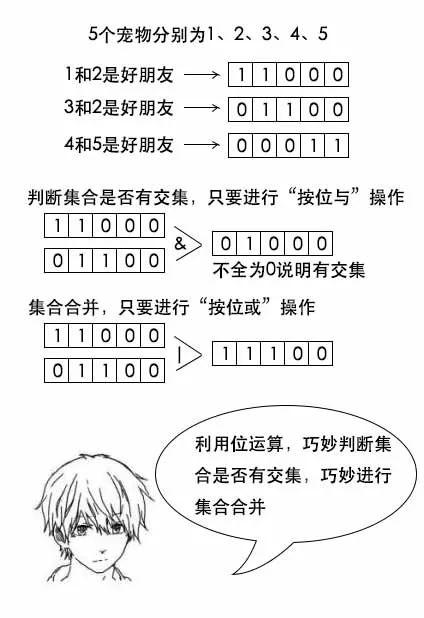
小史在纸上画了半天进行思考。一分钟过去了。

小史：我好像知道了，可以在遍历好友关系的同时，把他们进行合并，我用双向链表来做。初始时，每个宠物都是一个单独的节点，而一对好友关系过来的时候，先判断两个节点是否在同一个链表中，如果不在，就把两个节点所在的链表头尾相连，形成一个新链表。

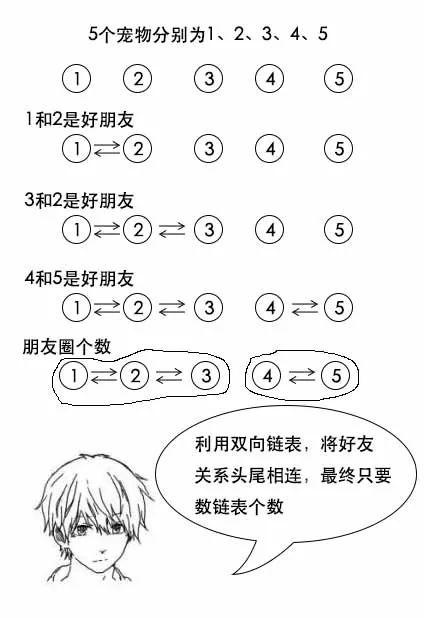
一分钟过去了。

请教大神

回到学校，小史把面试情况和吕老师说了一下。

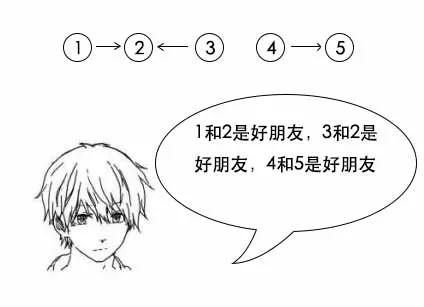
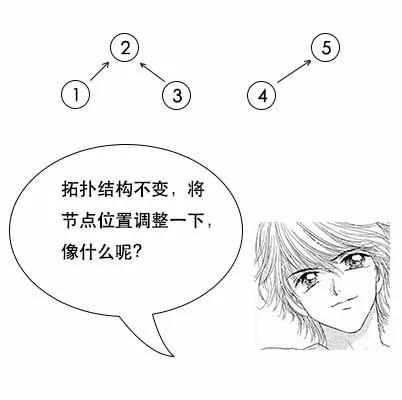
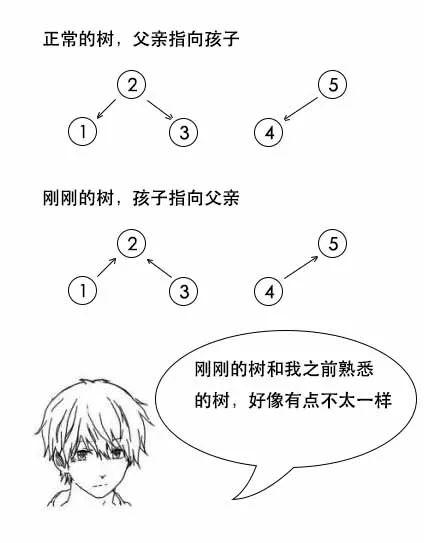
小史：这个我早就考虑到了，1和3是好朋友，并不是连接1和3，而是去找1的根和3的根，发现他们都是2，所以他们本来就在一个朋友圈，不需要相连。

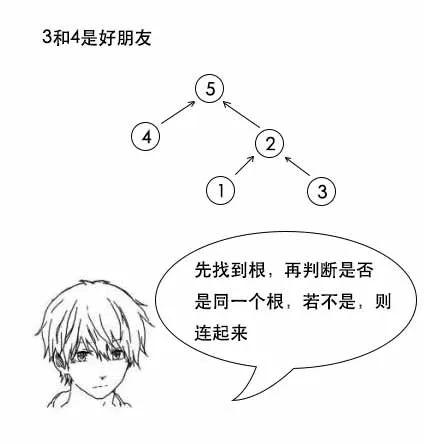
并查集

小史：哦，对，堆也是一种树，但是它是二叉树，而且是完全二叉树，所以才能用数组存，并且用坐标的方式计算父亲孩子节点。

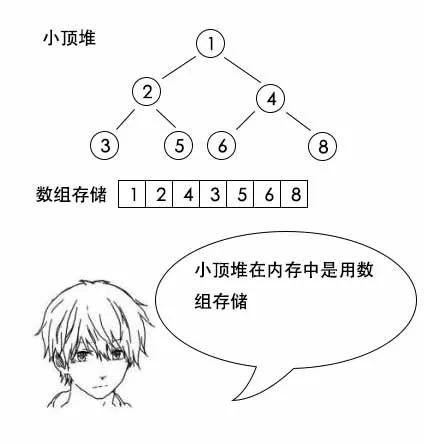
吕老师：今天的树同样可以用数组存，初始时刻数组中都是-1，当有两个节点需要合并时，只需要将其中一个数的根的值设为另一个数的根的下标就行。

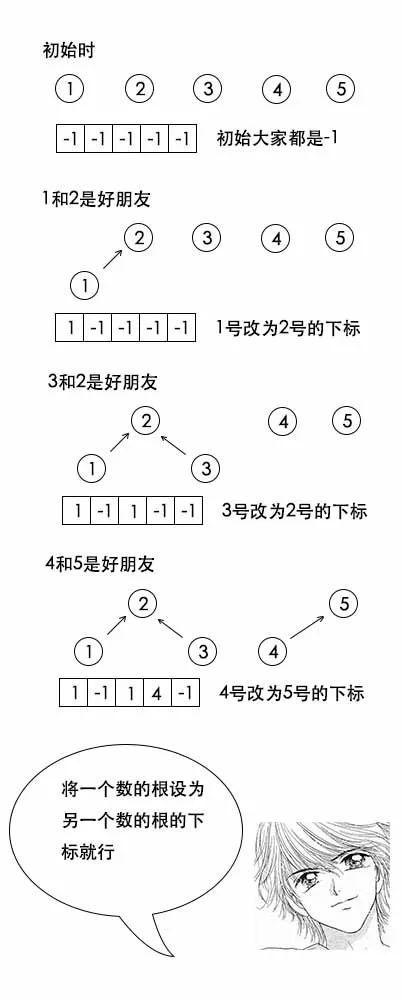
小史在纸上划拉半天，终于有点明白了。

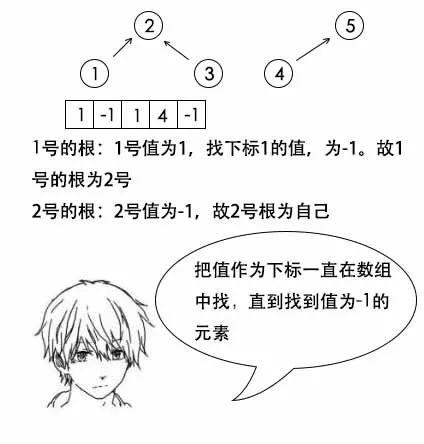
理解了算法之后，小史的代码写起来也是非常快，不一会儿就写好了。

UnionFindSet.java

/** * @author xiaoshi on 2018/11/4. */public class UnionFindSet {    // 存储并查集    private int[] elements;    UnionFindSet(int n) {        // 初始都为-1        elements = new int[n];        for (int i = 0; i < n; i++) {            elements[i] = -1;        }    }    // 找到一个数的根    public int find(int x) {        while(elements[x] != -1) {            x = elements[x];        }        return x;    }    // 把两个数的根连起来    public void union(int x, int y) {        // x的根        int rootx = find(x);        // y的根        int rooty = find(y);        // 如果不是同一个根就连起来        if(rootx != rooty) {            elements[rootx] = rooty;        }    }    // 计算形成了多少颗树    public int count() {        int count = 0;        for(int i=0; i<elements.length; i++) {            if(elements[i] == -1) {                count++;            }        }        return count;    }    // 打印并查集    public void print() {        for(int i=0; i<elements.length; i++) {            System.out.print(elements[i] + " ");        }        System.out.println();    }}

Main.java

/** * @author xiaoshi on 2018/11/4. */public class Main {    public static void main(String[] args) {        UnionFindSet ufs = new UnionFindSet(10);        ufs.union(0, 1);        ufs.union(0, 2);        ufs.union(3, 4);        ufs.union(3, 1);        ufs.union(5, 7);        ufs.union(7, 8);        ufs.union(7, 8);        System.out.println(ufs.count());    }}

运行结果

4

基于树高度的合并优化

吕老师：1和2是好朋友，2和3是好朋友，3和4是好朋友，4和5是好朋友。

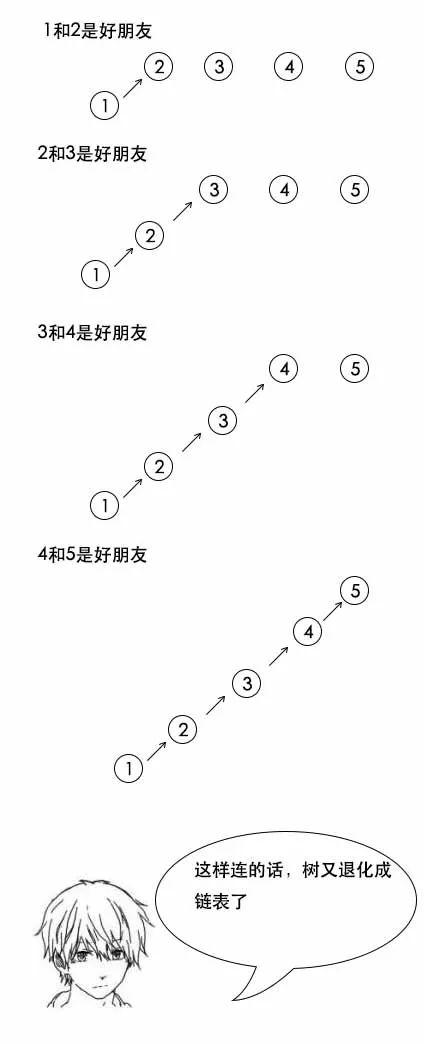
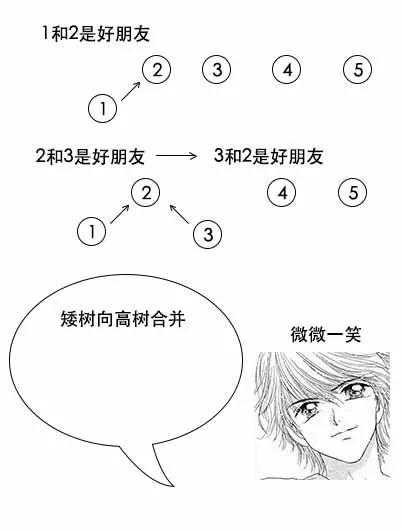
理解了算法之后，小史的代码写起来也是非常快，不一会儿就写好了。

UnionFindSetMergeOptimize.java

/** * @author xiaoshi on 2018/11/4. */public class UnionFindSetMergeOptimize {    // 存储并查集    private int[] elements;    // 存储树的高度    private int[] heights;    UnionFindSetMergeOptimize(int n) {        elements = new int[n];        heights = new int[n];        for (int i = 0; i < n; i++) {            // 初始都为-1            elements[i] = -1;            // 初始高度1            heights[i] = 1;        }    }    // 找到一个数的根    public int find(int x) {        while(elements[x] != -1) {            x = elements[x];        }        return x;    }    // 把两个数的根连起来    public void union(int x, int y) {        // x的根        int rootx = find(x);        // y的根        int rooty = find(y);        // 如果不是同一个根就连起来        if(rootx != rooty) {            // 矮树向高树合并            if(heights[rootx] > heights[rooty]) {                elements[rooty] = rootx;            } else if(heights[rootx] < heights[rooty]) {                elements[rootx] = rooty;            } else {                // 如果高度相同，随便合并                elements[rootx] = rooty;                // 但是记得合并后高度加一                heights[rooty]++;            }        }    }    // 计算形成了多少颗树    public int count() {        int count = 0;        for(int i=0; i<elements.length; i++) {            if(elements[i] == -1) {                count++;            }        }        return count;    }    // 打印并查集    public void print() {        for(int i=0; i<elements.length; i++) {            System.out.print(elements[i] + " ");        }        System.out.println();        for(int i=0; i<heights.length; i++) {            System.out.print(heights[i] + " ");        }        System.out.println();    }}

Main.java

/** * @author xiaoshi on 2018/11/4. */public class Main {    public static void main(String[] args) {        UnionFindSetMergeOptimize ufsmo = new UnionFindSetMergeOptimize(10);        ufsmo.union(0, 1);        ufsmo.union(1, 2);        ufsmo.union(2, 3);        ufsmo.union(3, 4);        ufsmo.union(4, 5);        ufsmo.union(5, 6);        ufsmo.union(6, 7);        ufsmo.union(7, 8);        ufsmo.union(8, 9);        System.out.println(ufsmo.count());    }}

运行结果

1

路径压缩优化

理解了算法之后，小史的代码写起来也是非常快，不一会儿就写好了。

UnionFindSetPathOptimize.java

/** * @author xiaoshi on 2018/11/4. */public class UnionFindSetPathOptimize {    // 存储并查集    private int[] elements;    UnionFindSetPathOptimize(int n) {        // 初始都为-1        elements = new int[n];        for (int i = 0; i < n; i++) {            elements[i] = -1;        }    }    // 找到一个数的根    public int find(int x) {        // 保存原始x值        int originX = x;        // 找到根        while(elements[x] != -1) {            x = elements[x];        }        // 把这一路的节点全部直接连到根上        while(originX != x) {            int tempX = originX;            originX = elements[originX];            elements[tempX] = x;        }        return x;    }    // 把两个数的根连起来    public void union(int x, int y) {        // x的根        int rootx = find(x);        // y的根        int rooty = find(y);        // 如果不是同一个根就连起来        if(rootx != rooty) {            elements[rootx] = rooty;        }    }    // 计算形成了多少颗树    public int count() {        int count = 0;        for(int i=0; i<elements.length; i++) {            if(elements[i] == -1) {                count++;            }        }        return count;    }    // 打印并查集    public void print() {        for(int i=0; i<elements.length; i++) {            System.out.print(elements[i] + " ");        }        System.out.println();    }}

Main.java

/** * @author xiaoshi on 2018/11/4. */public class Main {    public static void main(String[] args) {        UnionFindSetPathOptimize ufspo = new UnionFindSetPathOptimize(10);        ufspo.union(0, 1);        ufspo.union(1, 2);        ufspo.union(2, 3);        ufspo.union(3, 4);        ufspo.union(4, 5);        ufspo.union(5, 6);        ufspo.union(6, 7);        ufspo.union(7, 8);        ufspo.union(0, 9);        System.out.println(ufspo.count());    }}

运行结果：

1

看着自己写的代码，小史还是忍不住赞叹。

作者：channingbreeze，国内某互联网公司全栈开发。

声明：本文为作者投稿，版权归对方所有。

---

 热 文 推 荐 

☞ 微博回应裁员；罗永浩股权被冻结；“隐形贫困”人群最爱苹果 | 极客头条

☞ 快看，我们的分布式缓存就是这样把注册中心搞崩塌的！

☞ Linux 常用命令如何使用？

特别策划 | 盘点区块链的2018：技术与工具演进篇

☞ 企业云存储建设之路

开除“野狗”式程序员，团队的效率提高了

AI in 美团：吃喝玩乐背后的黑科技

☞ 老程序员肺腑忠告：千万别一辈子靠技术生存！

print_r('点个好看吧！');
var_dump('点个好看吧！');
NSLog(@"点个好看吧！");
System.out.println("点个好看吧！");
console.log("点个好看吧！");
print("点个好看吧！");
printf("点个好看吧！\n");
cout << "点个好看吧！" << endl;
Console.WriteLine("点个好看吧！");
fmt.Println("点个好看吧！");
Response.Write("点个好看吧！");
alert("点个好看吧！")
echo "点个好看吧！"

喜欢就点击“好看”吧！