戳蓝字“CSDN云计算”关注我们哦！

前一段时间，小灰发布了一篇有关大整数相加的漫画，没看过的小伙伴可以先看一看：

漫画：如何实现大整数相加？

那么，大整数相乘又是如何实现的呢？

起初，小灰认为只要按照大整数相加的思路稍微做一下变形，就可以轻松实现大整数相乘。但是随着深入的学习，小灰才发现事情并没有那么简单......

—————  第二天  —————

怎样列出这个乘法竖式呢？以 93281 X 2034 为例，竖式如下：

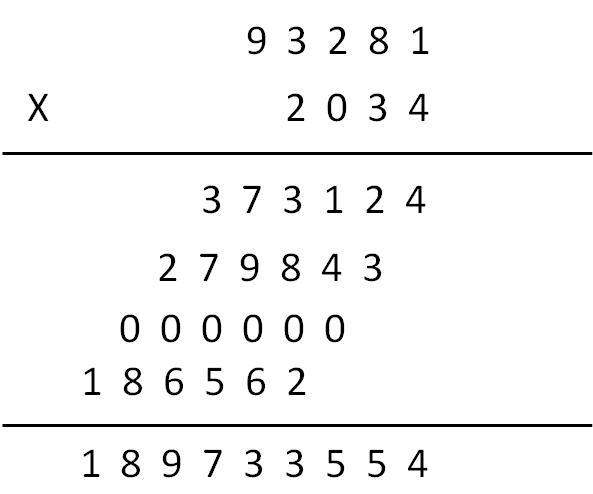
在程序中，我们可以利用int型数组，把两个大整数按位进行存储，再把数组中的元素像小学竖式那样逐个进行计算。

这个乘法竖式的计算过程可以大体分为两步：

1.整数B的每一个数位和整数A所有数位依次相乘，得到中间结果。

2.所有中间结果相加，得到最终结果。

1. /**

2. * 大整数求乘积

3. * @param bigNumberA  大整数A

4. * @param bigNumberB  大整数B

5. */

6. public static String multiply(String bigNumberA, String bigNumberB) {

7.    //1.把两个大整数用数组逆序存储，数组长度等于两整数长度之和

8.    int lengthA = bigNumberA.length();

9.    int lengthB = bigNumberB.length();

10.    int[] arrayA = new int[lengthA];

11.    for(int i=0; i< lengthA; i++){

12.        arrayA[i] = bigNumberA.charAt(lengthA-1-i) - '0';

13.    }

14.    int[] arrayB = new int[lengthB];

15.    for(int i=0; i< lengthB; i++){

16.        arrayB[i] = bigNumberB.charAt(lengthB-1-i) - '0';

17.    }

18.    //2.构建result数组，数组长度等于两整数长度之和

19.    int[] result = new int[lengthA+lengthB];

20.    //3.嵌套循环，整数B的每一位依次和整数A的所有数位相乘，并把结果累加

21.    for(int i=0;i

22.        for(int j=0;j

23.            //整数B的某一位和整数A的某一位相乘

24.            result[i+j] += arrayB[i]*arrayA[j];

25.            //如果result某一位大于10，则进位，进位数量是该位除以10的商

26.            if(result[i+j] >= 10){

27.                result[i+j+1] += result[i+j]/10;

28.                result[i+j] = result[i+j]%10;

29.            }

30.        }

31.    }

32.    //4.把result数组再次逆序并转成String

33.    StringBuilder sb = new StringBuilder();

34.    //是否找到大整数的最高有效位

35.    boolean findFirst = false;

36.    for (int i = result.length - 1; i >= 0; i--) {

37.        if(!findFirst){

38.            if(result[i] == 0){

39.                continue;

40.            }

41.            findFirst = true;

42.        }

43.        sb.append(result[i]);

44.    }

45.    return sb.toString();

46. }


48. public static void main(String[] args) {

49.    String x = "3338429042340042304302404";

50.    String y = "12303231";

51.    System.out.println(multiply(x, y));

52. }

————————————

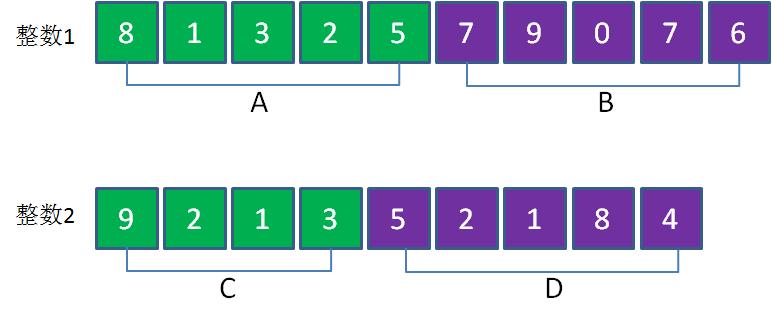
下面，我们的推导会有一些烧脑，请大家坐稳扶好~~

大整数从高位到低位，被平分成了两部分。设整数1的高位部分是A，低位部分是B；整数2的高位部分是C，低位部分是D，那么有如下等式：

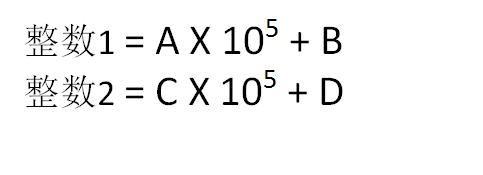
如果把大整数的长度抽象为n，那么：

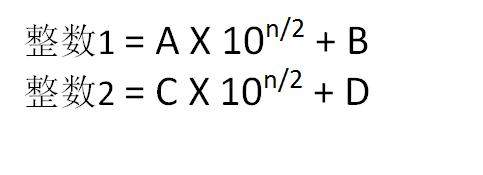
因此，整数1与整数2 的乘积可以写成下面的形式：

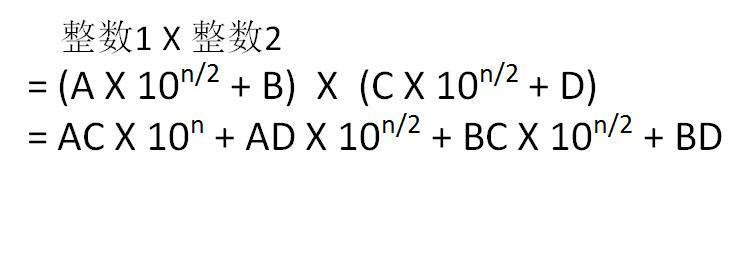
如此一来，原本长度为n的大整数的1次乘积，被转化成了长度为n/2的大整数的4次乘积（AC，AD，BC，BD）。

什么是master定理呢？

master定理的英语名称是master theorem，它为许多由分治法得到的递推关系式提供了渐进时间复杂度分析。

设常数a >= 1，b > 1，如果一个算法的整体计算规模 T(n) =  a T(n / b) + f(n)，那么则有如下规律：

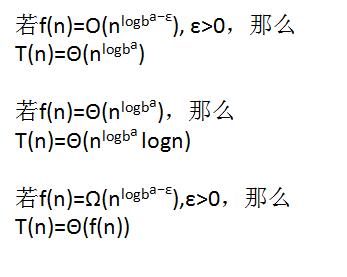
假设两个长度为n的大整数相乘，整体运算规模是T(n) 。

根据刚才得到的结论，两个大整数相乘被拆分成四个较小的乘积：

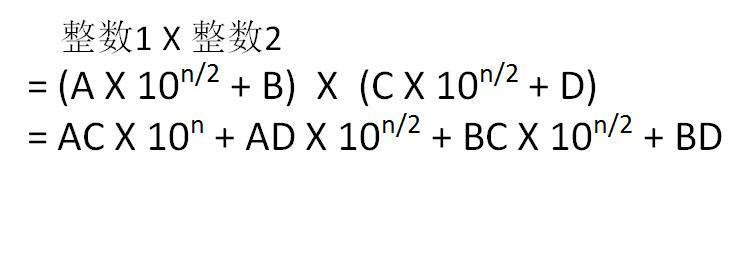
所以在第一次分治时，T(n)和T(n/2)有如下关系：

T(n) = 4T(n/2) + f(n)

其中f(n)是4个乘积结果相加的运算规模，f(n)的渐进时间复杂度很明显是O(n)。

把这个关系带入到master定理的公式 T(n) =  a T(n / b) + f(n) 当中，

此时 a=4， b=2。

此时，把a和b的值，以及f(n)的时间复杂度带入到master定理的第一个规律，也就是下面的规律：

发现正好符合条件。

怎么符合呢？推导过程如下：

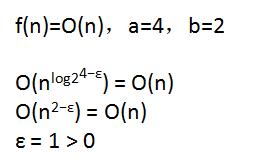
所以我们的平均时间复杂度是：

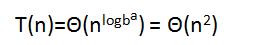
—————END—————

1.微信群：

添加小编微信：color_ld，备注“进群+姓名+公司职位”即可，加入【云计算学习交流群】，和志同道合的朋友们共同打卡学习！

2.征稿：

投稿邮箱：[email protected]；微信号：color_ld。请备注投稿+姓名+公司职位。

推荐阅读

• 细数华为核心技术家底：华为真会被击垮吗？

• 如何使用 Lucene 做网站高亮搜索功能？
  

• 20张图表达程序员的心酸

• 一个程序员父亲的呼吁：不要教你的孩子从小学编程！
  

• Python | 7招教你识别一个网站是否是Django后台
  

• 月薪 50K 大牛整理！6 张 Python 图谱，看完茅塞顿开！
  

程序人生公众号是CSDN旗下有影响力的开发者自媒体之一。这是一个以程序员日常工作和生活紧密相关且垂直服务于程序员群体的自媒体平台，扫描关注吧~

↓点击“阅读原文”，打开APP 阅读更顺畅