数据结构与算法分析（十二）--- 怎么实现并用好一个堆或优先队列？

文章目录

一、如何理解堆？

1.1 体育锦标赛如何赛出前几名？

如果你对体育赛事比较感兴趣，应该了解体育赛事的赛程安排和角逐出冠军、亚军、季军的方法和流程。在单淘汰的锦标赛中，选手们两两比赛，胜者晋级、败者被淘汰，比如世界乒乓球锦标赛或者大满贯网球赛就是这么进行的。这样一来，就可以把比赛的赛程和结果对应成一个二叉树，比如下图是17年美国公开赛的赛程安排，长得跟二叉树很想一模一样吧（觉得不像的话，可以把下图逆时针旋转90°再看）：
2017美国体育公开赛赛程
在上面的二叉树中，每一个选手是二叉树中的一个叶子结点，每一场比赛就相当于两个数字在比大小，数字大的选手获胜进入下一轮，也就是说比大小，大的那个选手进入上一层，成为枝干上的根。所以，进入到某一轮比赛的选手，其实都是某个子树干的根结点，最后的冠军自然就是整个二叉树的根结点。当然，这种赛制的合理性来自于下面一个假设：如果张三赢了李四，李四赢了王五，那么张三一定能赢王五，可以把这个假设称为“输赢的传递性”。

只要上面这种胜负的传递性成立，通过这种比赛的结果得到的冠军，一定是最好的选手。但是，第二名是否如此就难说了，因为冠军一路打下来，被他刷掉的选手可能水平都不差，只是运气不好，提前遇到他了，在决赛之前被淘汰了。比如说在某次网球比赛中，德约科维奇（人称小德）半决赛赢了费德勒，决赛赢了纳达尔，小德的冠军不会有什么异议，但你说到底是纳达尔该得亚军，还是费德勒更厉害，还真不好说，费德勒只能怪自己那次抽签运气不好。因此，如果真要较真，就需要把被冠军淘汰下来的人放到一个组里再相互比赛，才能知道谁是亚军。当然，如果体育比赛规则已经成型，大家遵守就好，不必那么麻烦赛出第二名。

但是，在工程中如果要对比两个数字的大小，总不能说哪个数字最后被最大的比下去，就是第二大的吧。因此，如果采用类似锦标赛的方法排出了一、二、三名来，第一大的数字可以完全按照锦标赛淘汰制的方式来。但是第二大的数字，就需要从所有与最大数字比较过被淘汰的数字中，再次比较选择才能确定，当第二大的数字确定后，就可以用这种方法找到第三大的数字了。这种算法，由于受到锦标赛的启发，因此被称为“锦标赛排序法（也称为树形选择排序）”，这种方法可分为两步：

  1. 第一步，把所有的数字放到二叉树中的叶子结点，然后按照锦标赛单淘汰的方式，两两比较选出最大的；
  2. 第二步，对于第二大的，从所有被最大的数字淘汰的数字中选择。比如在某次比赛中，被小德淘汰的分别是纳达尔、费德勒、穆雷等人，那么这些人再进行单淘汰，选亚军。对于第三、第四大的数字，可以以此类推。

如果用这种方法将所有的数字排序，由于除了第一大数字外，后面的每一个次大的数字仅需log2n次比较，故树形选择排序算法的时间复杂度是O(NlogN)，和快速排序差不多。那么为什么不直接使用快速排序，而要发明出这样一种不太容易理解的算法呢？因为在特定场合下，它更快速。比如说，如果我们只需要选出第一名，这种算法的复杂度只有O(N)，如果还需要选出第二名，则额外增加O(logN)次计算就可以了，对第三名也是如此。也就是说，锦标赛排序算法在从N个选手中选出K个选手的事情中特别快。

从前面的分析可以看出，虽然锦标赛排序法从N个选手中选出K个选手比较快速高效，但在实际工程中，所有的有效数据都在叶子结点，需要向上构建出整棵二叉树来保存每轮比赛的比较结果，这就需要额外占用O(N)的内存地址空间。

为了改善树形选择排序的缺点，1964年提出了新的排序算法 — 堆排序。什么是堆呢？堆排序又是如何巧妙改善树形选择排序算法缺点的呢？

1.2 什么是堆？

堆排序既然是从树形选择排序演化而来，二者之间就会有很大的相似性，在单淘汰锦标赛中，某个子树干根结点的选手成绩肯定是优于其左右两个子结点选手的，且在赛出冠军的过程中，各场比赛构成的二叉树是一棵完全二叉树。

堆也继承了锦标赛排序树的这两个特性，也就是说，堆是满足下面两个要求的二叉树：

  1. 堆是一个完全二叉树；
  2. 堆中每个节点的值都大于等于（或者小于等于）其左右子节点的值。

对于每个节点的值都大于等于子树中每个节点值的堆，我们叫作“大顶堆”；对于每个节点的值都小于等于子树中每个节点值的堆，我们叫作“小顶堆”。有了清晰的定义，下面给出几个二叉树，你能判断其是不是堆吗？
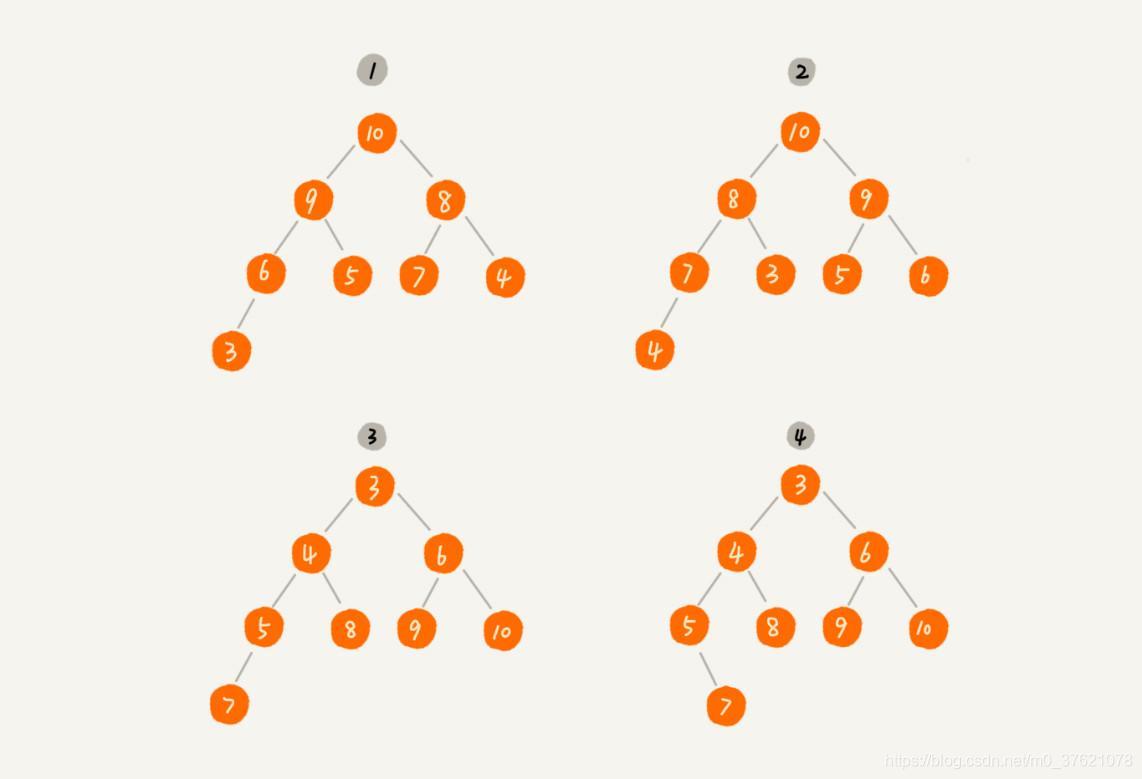
几棵二叉树是不是堆
其中第 1 个和第 2 个是大顶堆，第 3 个是小顶堆，第 4 个不是堆。除此之外，从图中还可以看出来，对于同一组数据，我们可以构建多种不同形态的堆。

二、堆与堆排序的实现

2.1 如何实现一个堆？

要实现一个堆，我们先要知道，堆都支持哪些操作以及如何存储一个堆。我们之前介绍过，完全二叉树比较适合用数组来存储，用数组来存储完全二叉树是非常节省存储空间的。因为我们不需要存储左右子节点的指针，单纯地通过数组的下标，就可以找到一个节点的左右子节点和父节点。下图是一个用数组存储堆的例子：
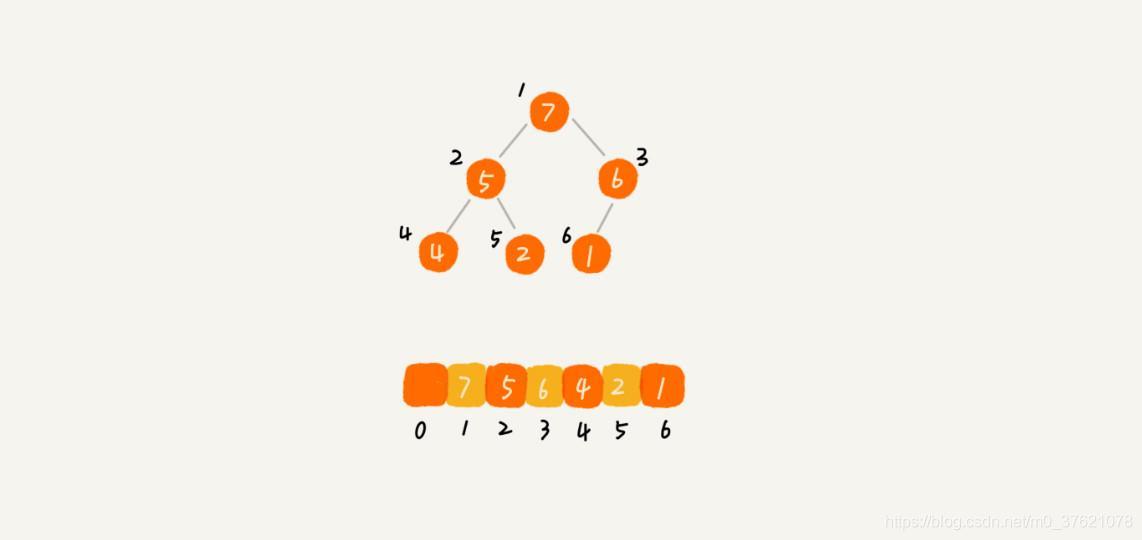
数组存储堆的图示
从图中我们可以看到，数组中下标为 i 的节点的左子节点，就是下标为 i∗2 的节点，右子节点就是下标为 i∗2+1 的节点，父节点就是下标为 i/2​ 的节点。

为了方便查看堆的容量和已存储的元素数量，我们可以使用一个结构体来描述一个堆，数据结构实现代码如下：

// datastruct\heap.c

struct HeapStruct{
    int capacity;
    int size;
    DataType *Array;
};
typedef struct HeapStruct *pHeap;

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8

知道了如何存储一个堆，那我们再来看看，堆上的操作有哪些呢？我罗列了几个非常核心的操作，分别是往堆中插入一个元素和删除堆顶元素。（如果没有特殊说明，下面都是拿大顶堆举例）。

  • 往堆中插入一个元素

往堆中插入一个元素后，我们需要继续满足堆的两个特性。如果我们把新插入的元素放到堆的最后，插入新元素后就不符合堆的特性了，我们就需要对其进行调整，让其重新满足堆的特性，这个过程我们可以称作堆化（heapify），堆化实际上有两种，从下往上和从上往下。

我先看从下往上的堆化方法，堆化非常简单，就是顺着节点所在的路径，向上或者向下，对比，然后交换。我们可以让新插入的节点与父节点对比大小，如果不满足子节点小于等于父节点的大小关系，我们就互换两个节点。一直重复这个过程，直到父子节点之间满足堆要求的大小关系。下面给出一个从下往上堆化的过程分解图供参考：
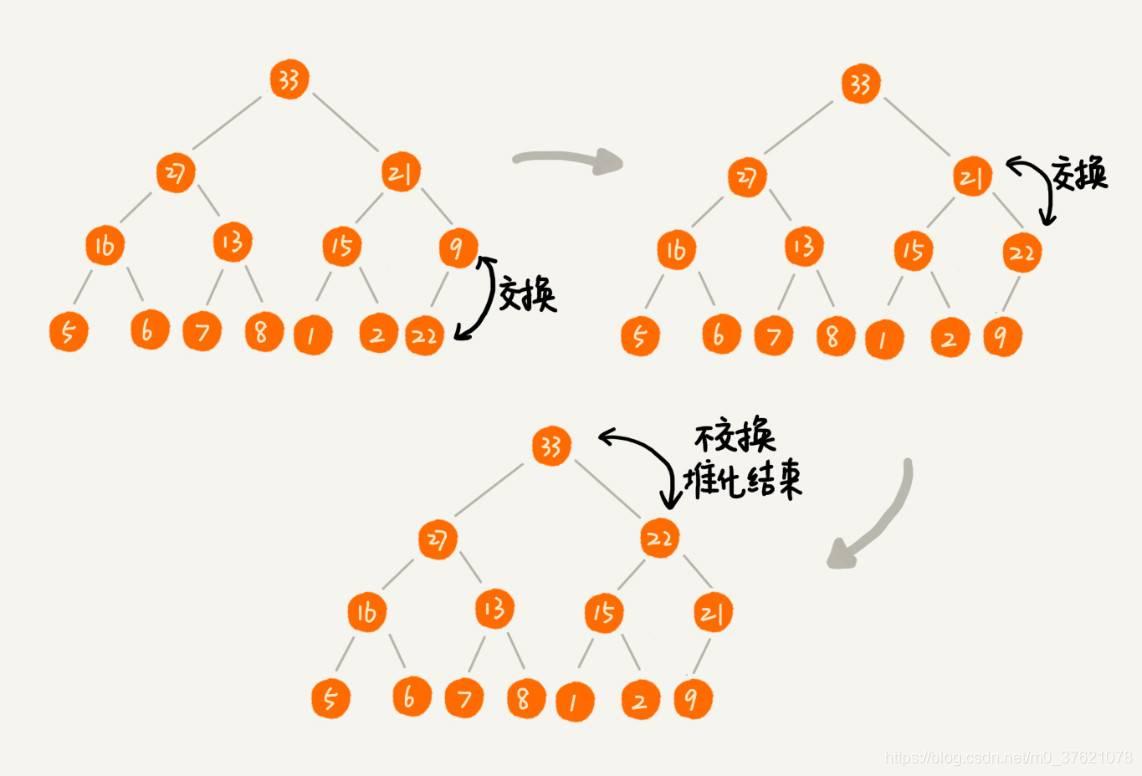
从下往上堆化过程
按照上述逻辑，编写往堆中插入数据的实现代码如下：

// datastruct\heap.c

void swap_data(int *a, int *b);

void Heap_Insert(pHeap H, DataType x)
{
    if(H->size >= H->capacity)
        return;

    int i;
    H->size++;
    H->Array[H->size] = x;
    // 自下往上堆化
    for(i = H->size; i/2 > 0 && H->Array[i] > H->Array[i/2]; i /= 2)
        swap_data(&H->Array[i], &H->Array[i/2]); 
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16

删除堆顶元素

从堆的定义的第二条中，任何节点的值都大于等于（或小于等于）子树节点的值，我们可以发现，堆顶元素存储的就是堆中数据的最大值或者最小值。

假设我们构造的是大顶堆，堆顶元素就是最大的元素。当我们删除堆顶元素之后，就需要把第二大的元素放到堆顶，那第二大元素肯定会出现在左右子节点中。然后我们再迭代地删除第二大节点，以此类推，直到叶子节点被删除。不过这种方法有点问题，就是最后堆化出来的堆并不满足完全二叉树的特性，比如下图所示：
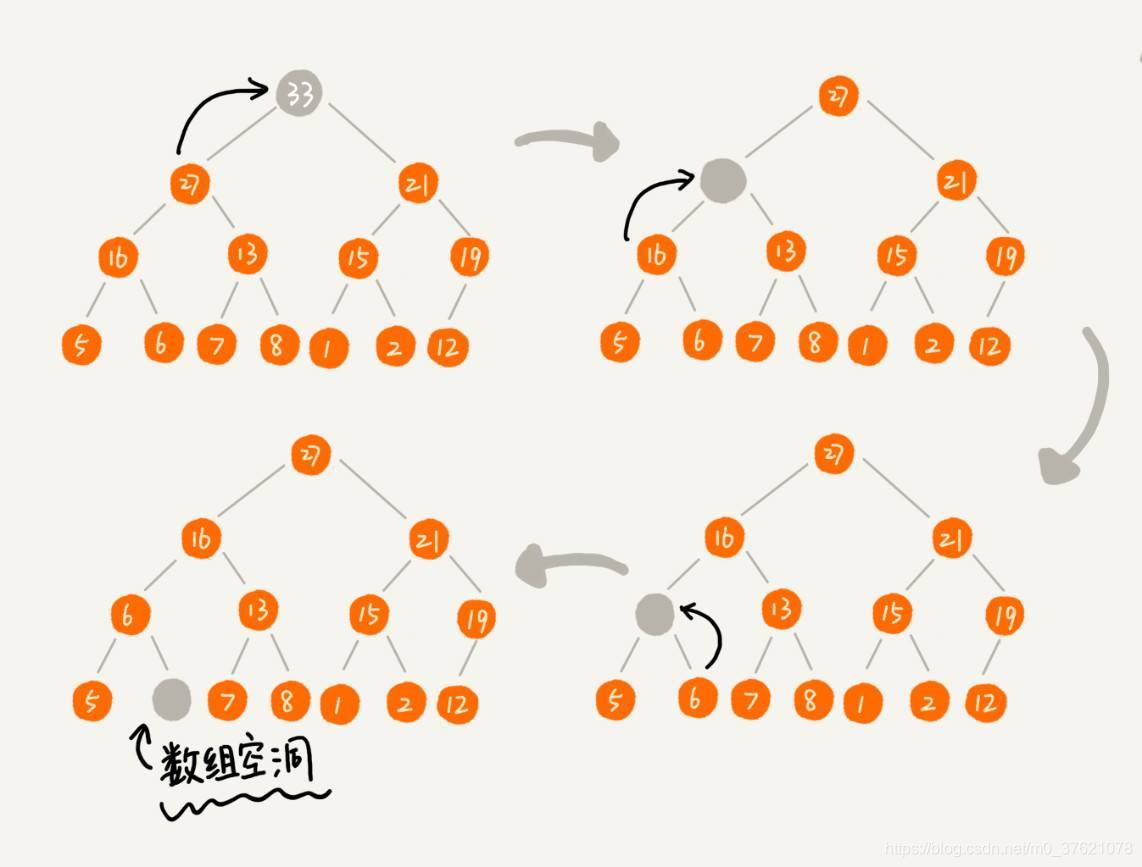
删除堆顶元素出现数组空洞
实际上，我们稍微改变一下思路，就可以解决这个问题。我们把最后一个节点放到堆顶，然后利用同样的父子节点对比方法。对于不满足父子节点大小关系的，互换两个节点，并且重复进行这个过程，直到父子节点之间满足大小关系为止，这就是从上往下的堆化方法，分解图示如下：
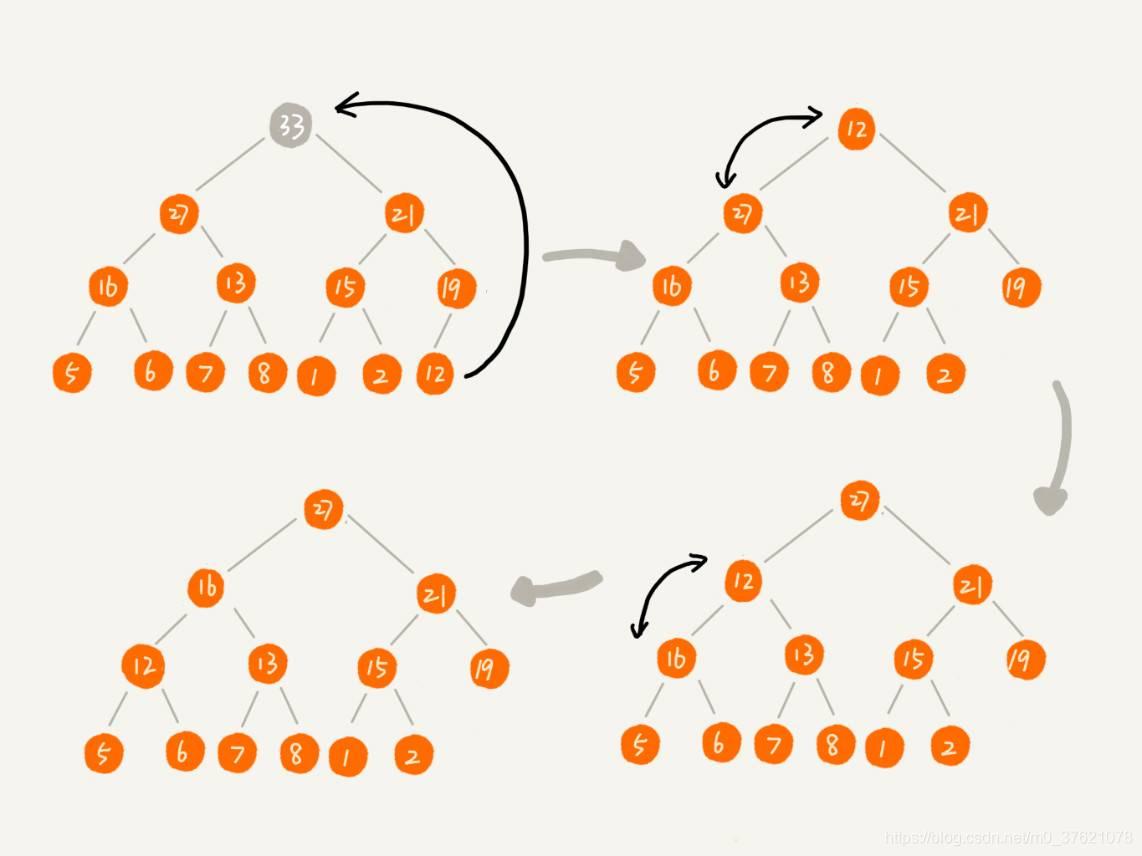
从上往下的堆化过程
因为我们移除的是数组中的最后一个元素，而在堆化的过程中，都是交换操作，不会出现数组中的“空洞”，所以这种方法堆化之后的结果，肯定满足完全二叉树的特性。

按照上述逻辑，编写删除堆顶元素的实现代码如下：

// datastruct\heap.c

DataType Heap_RemoveTop(pHeap H)
{
    if(H->size <= 0)
        return -1;

    int i, maxPos;
    H->Array[0] = H->Array[1];
    H->Array[1] = H->Array[H->size];
    H->size--;
    // 自上往下堆化
    for(i = 1; 2 * i <= H->size; i = maxPos)
    {
        maxPos = i;
        if(H->Array[i] < H->Array[2 * i])
            maxPos = 2 * i;
        if(2 * i + 1 <= H->size && H->Array[maxPos] < H->Array[2 * i + 1])
            maxPos = 2 * i + 1;
        if(maxPos == i)
            break;

        swap_data(&H->Array[i], &H->Array[maxPos]);
    }
    return H->Array[0];
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26

我们编写一个堆插入删除元素的示例程序，验证前面实现的两个操作函数是否有bug，示例程序代码如下：

// datastruct\heap.c

#include 
#include 

#define DataType    int

struct HeapStruct{
    int capacity;
    int size;
    DataType *Array;
};
typedef struct HeapStruct *pHeap;

pHeap Heap_Create(int capacity)
{
    pHeap H = malloc(sizeof(struct HeapStruct));
    if(H == NULL)
    {
        printf("Out of space.");
        return NULL;
    }

    H->Array = malloc((capacity + 1) * sizeof(DataType));
    if(H->Array == NULL)
    {
        printf("Out of space.");
        free(H);
        return NULL;
    }

    H->capacity = capacity;
    H->size = 0;
    return H;
}

void swap_data(int *a, int *b);
void Heap_Insert(pHeap H, DataType x);
DataType Heap_RemoveTop(pHeap H);

void HeapPrintf(pHeap H)
{
    int i;

    printf("Heap element: \n");
    for(i = 1; i < H->size; i++)
        printf("%d ", H->Array[i]);
    printf("\n");
}

int main(void)
{
    pHeap H = Heap_Create(100);
    Heap_Insert(H, 1);
    Heap_Insert(H, 2);
    Heap_Insert(H, 3);
    Heap_Insert(H, 4);
    Heap_Insert(H, 5);
    Heap_Insert(H, 6);
    Heap_Insert(H, 7);
    Heap_Insert(H, 8);
    Heap_Insert(H, 9);

    HeapPrintf(H);

    printf("Remove heap top: %d\n", Heap_RemoveTop(H));
    printf("Remove heap top: %d\n", Heap_RemoveTop(H));

    HeapPrintf(H);

    return 0;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59
  • 60
  • 61
  • 62
  • 63
  • 64
  • 65
  • 66
  • 67
  • 68
  • 69
  • 70
  • 71
  • 72

上面堆的示例程序运行结果如下：
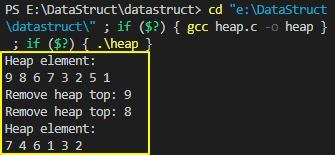
堆的插入/删除示例程序运行结果
一个包含 n 个节点的完全二叉树，树的高度不会超过 log2​n。堆化的过程是顺着节点所在路径比较交换的，所以堆化的时间复杂度跟树的高度成正比，也就是 O(logn)。插入数据和删除堆顶元素的主要逻辑就是堆化，所以，往堆中插入一个元素和删除堆顶元素的时间复杂度都是 O(logn)。

2.2 如何基于堆实现排序？

我们借助于堆这种数据结构实现的排序算法，就叫作堆排序。这种排序方法的时间复杂度非常稳定，是 O(nlogn)，并且它还是原地排序算法。如此优秀，它是怎么做到的呢？我们可以把堆排序的过程大致分解成两个大的步骤，建堆和排序。

  • 建堆

我们首先将数组原地建成一个堆，所谓“原地”就是，不借助另一个数组，就在原数组上操作。

我们可以借助前面实现往堆中插入一个元素的操作，将原数组分为已完成堆化的部分和剩余元素两部分，不断从后半部分取出首元素插入到前面的堆中，待后半部分元素全部插入前半部分的堆中，原数组就完成了建堆操作（这个处理技巧在前面介绍的插入排序中也用到了）。

但这个过程有点问题，前面介绍堆实现过程时，下标为 0 的存储单元并未使用，使用的存储单元比实际元素个数多 1 个，我们要建堆的原数组可能都是有效元素，使用上面的思路实现就需要对下标为 0 的元素单独处理，或者对原数组进行扩容处理，有没有更好的处理方法呢？

如果堆中的数据从数组下标为 0 的存储单元开始，那么计算子节点和父节点的下标的公式有什么变化呢？假如节点的下标是 i，那左子节点的下标就是 2∗i + 1，右子节点的下标就是 2∗i + 2，父节点的下标就是 (i−1) / 2​。按照新的公式改写往堆中插入元素的函数代码如下：

// algorithm\sort.c

void Heap_Insert(pHeap H, DataType x)
{
    if(H->size >= H->capacity)
        return;

    int i;
    H->Array[H->size] = x;
    H->size++;
    // 自下往上堆化
    for(i = H->size - 1; i - 1 >= 0 && H->Array[i] > H->Array[(i-1)/2]; i = (i-1)/2)
        swap_data(&H->Array[i], &H->Array[(i-1)/2]);
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14

按照上述逻辑，对一个数组进行原地建堆的实现代码如下：

// algorithm\sort.c

pHeap Build_Heap(DataType *Arry, int n)
{
    pHeap H = malloc(sizeof(struct HeapStruct));
    if(H == NULL)
    {
        printf("Out of space.");
        return NULL;
    }

    int i;
    H->Array = Arry;
    H->capacity = n;
    H->size = 0;
    
    for(i = 0; i < n; i++)
        Heap_Insert(H, Arry[i]);

    return H;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21

现在，我们来看，建堆操作的时间复杂度是多少呢？每个节点堆化的时间复杂度是 O(logn)，那 n 个节点堆化的总时间复杂度是不是就是 O(nlogn) 呢？这个答案虽然也没错，但是这个值还是不够精确。实际上，堆排序的建堆过程的时间复杂度是 O(n)，下面来推导一下。

每个节点堆化的过程中，需要比较和交换的节点个数，跟这个节点的高度 k 成正比。我们只需要将每个节点的高度求和，得出的就是建堆的时间复杂度。每一层的节点个数和对应的高度图示如下：
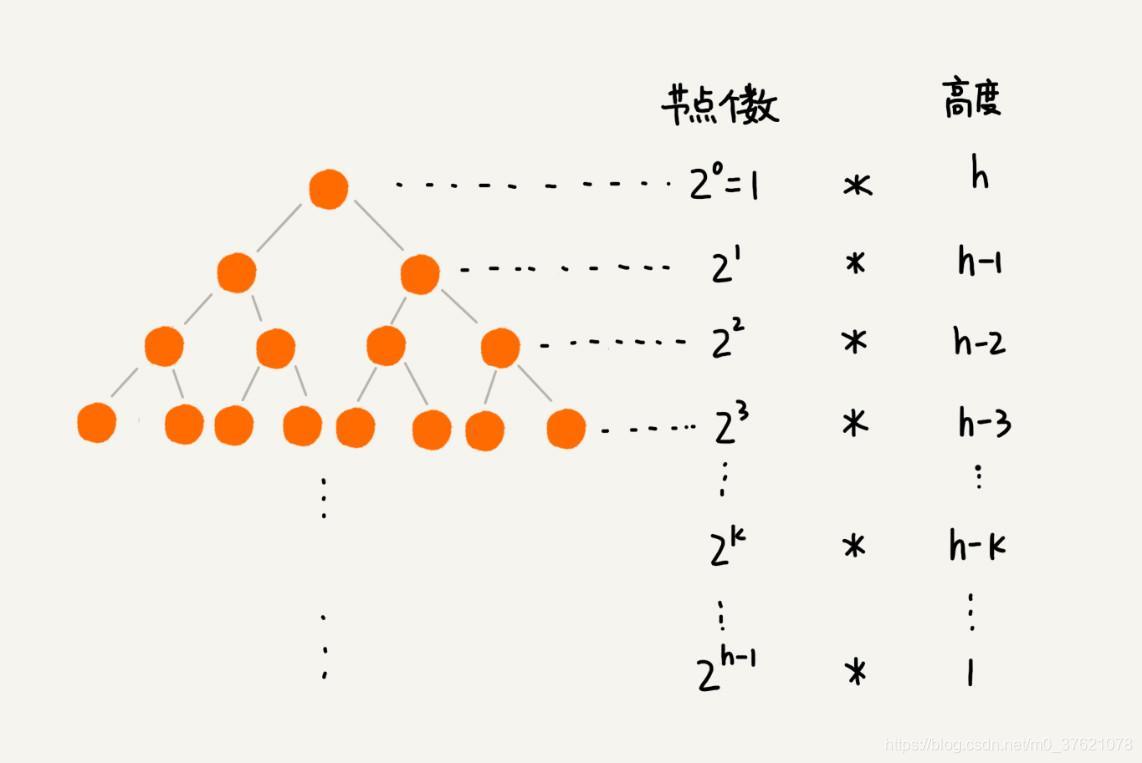
结点个数与高度关系图示
我们将每个非叶子节点的高度求和，就是下面这个公式：
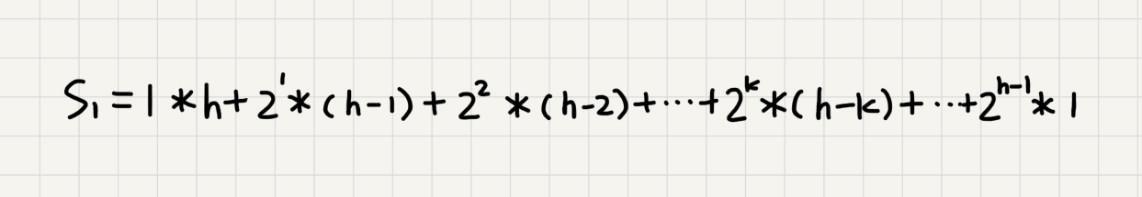
每层结点个数与高度乘积求和
这个公式的求解稍微有点技巧，不过我们高中应该都学过：把公式左右都乘以 2，就得到另一个公式 S2。我们将 S2 错位对齐，并且用 S2 减去 S1，可以得到 S。
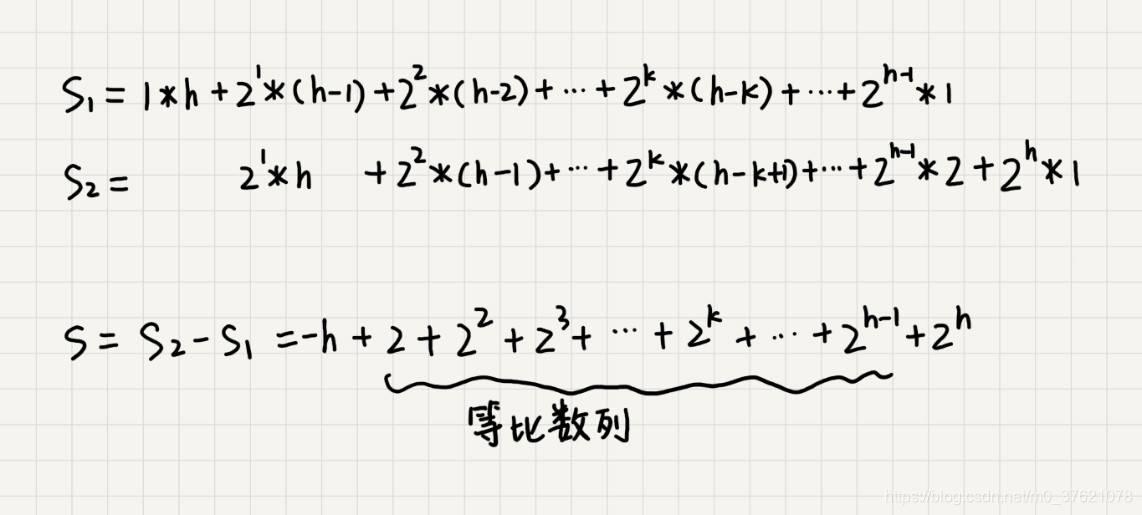
错位求和-等比数列
S 的中间部分是一个等比数列，所以最后可以用等比数列的求和公式来计算，最终的结果就是下面图中画的这个样子：
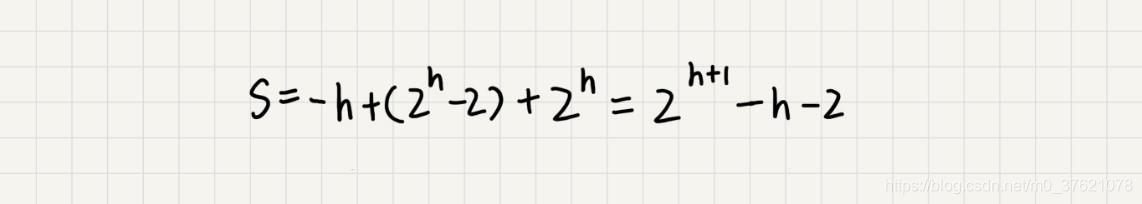
等比数列求和结果
因为 h=log2​n，代入公式 S，就能得到 S=O(n)，所以，建堆的时间复杂度就是 O(n)。

  • 排序

建堆结束之后，数组中的数据已经是按照大顶堆的特性来组织的。数组中的第一个元素就是堆顶，也就是最大的元素。我们把它跟最后一个元素交换，那最大元素就放到了下标为 n 的位置。

这个过程有点类似上面讲的“删除堆顶元素”的操作，当堆顶元素移除之后，我们把下标为 n 的元素放到堆顶，然后再通过堆化的方法，将剩下的 n−1 个元素重新构建成堆。堆化完成之后，我们再取堆顶的元素，放到下标是 n−1 的位置，一直重复这个过程，直到最后堆中只剩下标为 1 的一个元素，排序工作就完成了，该过程的分解图示如下：
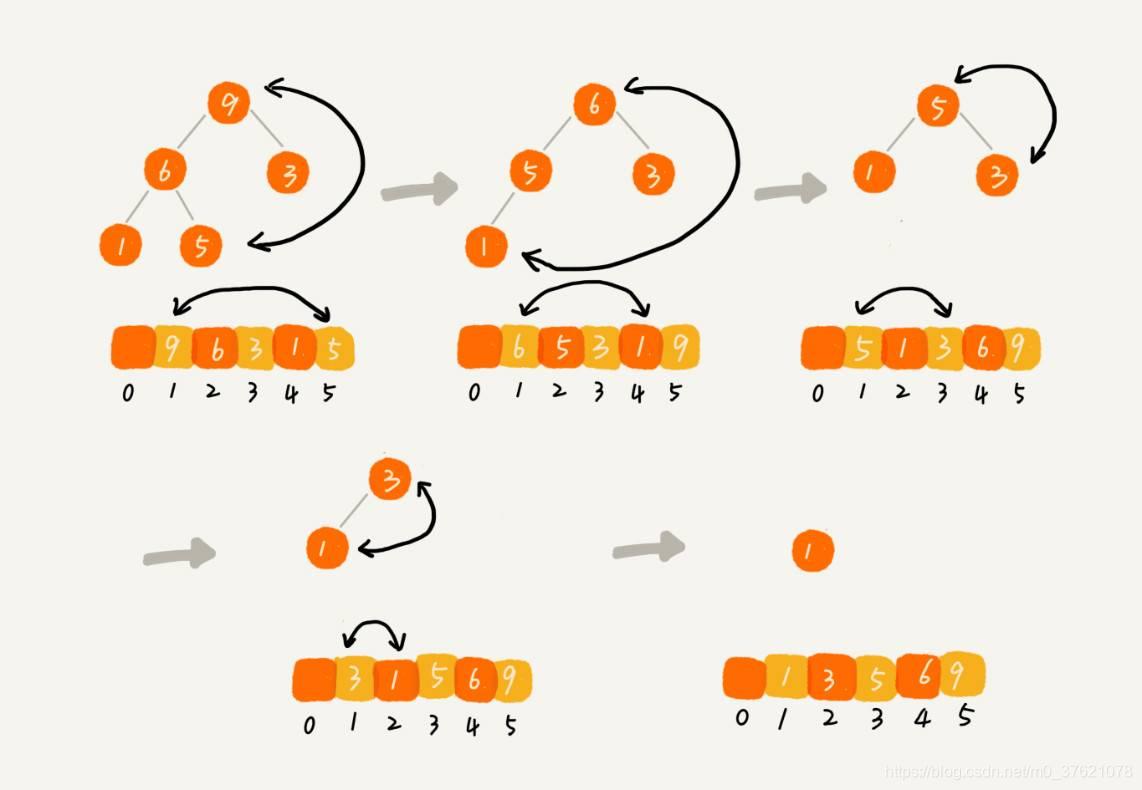
堆排序分解图示
我们按照堆从数组下标为 0 的存储单元开始，计算子节点与父节点的新公式，改写前面删除堆顶元素的函数代码如下：

// algorithm\sort.c

DataType Heap_RemoveTop(pHeap H)
{
    if(H->size <= 0)
        return -1;

    int i, maxPos;
    int top = H->Array[0];
    swap_data(&H->Array[0], &H->Array[H->size - 1]);
    H->size--;
    // 自上往下堆化
    for(i = 0; (2 * i + 1) <= H->size - 1; i = maxPos)
    {
        maxPos = i;
        if(H->Array[i] < H->Array[2 * i + 1])
            maxPos = 2 * i + 1;
        if((2 * i + 2) <= H->size - 1 && H->Array[maxPos] < H->Array[2 * i + 2])
            maxPos = 2 * i + 2;
        if(maxPos == i)
            break;

        swap_data(&H->Array[i], &H->Array[maxPos]);
    }

    return top;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27

按照上述逻辑，编写堆排序的实现代码如下：

// algorithm\sort.c

void Heap_Sort(DataType *Arry, int n)
{
    pHeap H = Build_Heap(Arry, n);
    if(H == NULL)
        return;

    while(H->size > 0)
        Heap_RemoveTop(H);

    free(H);
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13

现在，我们再来分析一下堆排序的时间复杂度、空间复杂度以及稳定性。

整个堆排序的过程，都只需要极个别临时存储空间，所以堆排序是原地排序算法。堆排序包括建堆和排序两个操作，建堆过程的时间复杂度是 O(n)，排序过程的时间复杂度是 O(nlogn)，所以，堆排序整体的时间复杂度是 O(nlogn)。

堆排序不是稳定的排序算法，因为在排序的过程，存在将堆的最后一个节点跟堆顶节点互换的操作，所以就有可能改变值相同数据的原始相对顺序。

  • 堆排序与快速排序优劣对比

下面使用一组百万规模的随机数据，跟快速排序对比下执行效率，对比结果如下：
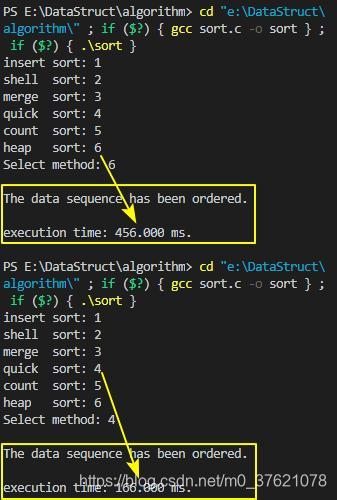
堆排序与快速排序对比结果
从上面的对比结果也可以看出，虽然堆排序与快速排序的平均时间复杂度都是 O(nlogn)，但在实际工程中，如果要对数据序列进行全排序，快速排序的性能明显高于堆排序，主要有以下几个原因：

  1. 堆排序数据访问的方式没有快速排序对CPU缓存友好。对于快速排序来说，数据是顺序访问的，而对于堆排序来说，数据是跳着访问的。 所以，堆排序的数据访问方式对 CPU 缓存是不友好的；
  2. 对于同样的数据，在排序过程中，堆排序算法的数据交换次数要多于快速排序。堆排序的第一步是建堆，建堆的过程会打乱数据原有的相对先后顺序，导致原数据的有序度降低。比如，对于一组已经有序的数据来说，经过建堆之后，数据反而变得更无序了。

堆排序相比快速排序的优势就是从N个数据中选出K个最大或最小的数据效率更高，比如大顶堆选出最大元素因需要建堆操作，时间复杂度为O(N)，后面选出第二大、第三大……第K大元素的时间复杂度均为O(logN)。

三、堆的应用

3.1 优先级队列

优先级队列，顾名思义，它首先应该是一个队列，队列最大的特性就是先进先出。不过，在优先级队列中，数据的出队顺序不是先进先出，而是按照优先级来，优先级最高的，最先出队。
优先队列基本模型
如何实现一个优先级队列呢？方法有很多，但是用堆来实现是最直接、最高效的。这是因为，堆和优先级队列非常相似。一个堆就可以看作一个优先级队列。很多时候，它们只是概念上的区分而已。往优先级队列中插入一个元素，就相当于往堆中插入一个元素；从优先级队列中取出优先级最高的元素，就相当于取出堆顶元素。

你可别小看这个优先级队列，它的应用场景非常多。我们后面要讲的很多数据结构和算法都要依赖它。比如，哈夫曼编码、图的最短路径、最小生成树算法等等。不仅如此，很多语言中，都提供了优先级队列的实现，比如，Java 的 PriorityQueue，C++ 的 priority_queue 等。我们先看看C++中的priority_queue容器是怎么使用的？再举两个具体的例子，感受一下优先级队列具体是怎么用的？

3.1.1 优先级队列STL容器简介(C++11)

C++标准库为优先级队列提供的STL容器是： class priority_queue<>，其中的元素依优先级被读取，它的接口和queue非常相近，即push()将会放入一个元素，top()/pop()将会访问/移除下一个元素。然而这里所谓”下一个元素“并非第一个放入的元素，而是”优先级最高“的元素。
priority queue接口
C++11 STL priority_queue的类模板定义如下（第一个参数T为元素类型，第二个参数Container定义priority_queue内部用来存放元素的实际容器，默认采用vector，第三个参数Compare定义”用以查找下一个最高优先级元素“的排序准则，默认以operator < 作为比较准则，也即构造为大顶堆）：

// 

namespace std{
	template <typename T,
			  typename Container = vector<T>,
			  typename Compare = less<typename Container::value_type>>
	class priority_queue;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8

实际上priority queue只是很单纯的把各项操作转化为内部容器的对应调用，你可以使用任何线性表容器支持priority queue，只要它们支持random-access iterator和front()、push_back()、pop_back()等操作就行。

如果要定义自己的比较准则，就必须传递一个函数（或function object）作为binary predicate，用以比较两个元素并以此作为排序准则，按照priority queue的默认排序准则，”下一个元素“始终是元素值最大者。

Priority queue容器的核心接口也就三个（当然还有比如查询大小size()、判断是否为空empty()等辅助接口）：

  • push(): 将一个元素放入priority queue中；
  • top(): 返回priority queue内的下一个元素；
  • pop(): 从priority queue中移除一个元素。

下面给出一个priority queue应用示例程序供参考：

// datastruct\priority_queue_demo.cpp

#include 
#include 

int main(void)
{
    std::priority_queue<float> pq;

    //insert three elements into the priority queue
    pq.push(66.6);
    pq.push(22.2);
    pq.push(44.4);

    // read and print two elements
    std::cout << pq.top() << ' ';
    pq.pop();
    std::cout << pq.top() << std::endl;
    pq.pop();

    //insert three more elements
    pq.push(11.1);
    pq.push(55.5);
    pq.push(33.3);

    // skip one element
    pq.pop();

    // pop and print remaining elements
    while (!pq.empty())
    {
        std::cout << pq.top() << ' ';
        pq.pop();
    }
    std::cout << std::endl;

    return 0;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38

上面priority queue的示例代码运行结果如下（需要注意编译器是否支持C++11，比如g++在4.7以上版本才支持，添加-std=c++11即可）：
priority queue示例代码运行结果

3.1.2 使用优先级队列合并有序小文件

假设我们有 100 个小文件，每个文件的大小是 100MB，每个文件中存储的都是有序的字符串。我们希望将这些 100 个小文件合并成一个有序的大文件，这里就会用到优先级队列。

整体思路有点像归并排序中的合并函数。我们从这 100 个文件中，各取第一个字符串，放入数组中，然后比较大小，把最小的那个字符串放入合并后的大文件中，并从数组中删除。假设，这个最小的字符串来自于 13.txt 这个小文件，我们就再从这个小文件取下一个字符串，放到数组中，重新比较大小，并且选择最小的放入合并后的大文件，将它从数组中删除。依次类推，直到所有的文件中的数据都放入到大文件为止。

这里我们用数组这种数据结构，来存储从小文件中取出来的字符串。每次从数组中取最小字符串，都需要循环遍历整个数组，时间复杂度为O(n)，显然，这不是很高效。有没有更加高效方法呢？

这里就可以用到优先级队列，也可以说是堆。我们将从小文件中取出来的字符串放入到小顶堆中，那堆顶的元素，也就是优先级队列队首的元素，就是最小的字符串。我们将这个字符串放入到大文件中，并将其从堆中删除。然后再从小文件中取出下一个字符串，放入到堆中。循环这个过程，就可以将 100 个小文件中的数据依次放入到大文件中。删除堆顶数据和往堆中插入数据的时间复杂度都是 O(logn)，很显然比原来数组存储的方式高效的多。

3.1.3 使用优先级队列实现高性能定时器

假设我们有一个定时器，定时器中维护了很多定时任务，每个任务都设定了一个要触发执行的时间点。定时器每过一个很小的单位时间（比如 1 秒），就扫描一遍任务，看是否有任务到达设定的执行时间。如果到达了，就拿出来执行。

但是，这样每过 1 秒就扫描一遍任务列表的做法比较低效，主要原因有两点：第一，任务的约定执行时间离当前时间可能还有很久，这样前面很多次扫描其实都是徒劳的；第二，每次都要扫描整个任务列表，如果任务列表很大的话，势必会比较耗时。

针对这些问题，我们就可以用优先级队列来解决。我们按照任务设定的执行时间，将这些任务存储在优先级队列中，队列首部（也就是小顶堆的堆顶）存储的是最先执行的任务。

这样，定时器就不需要每隔 1 秒就扫描一遍任务列表了。它拿队首任务的执行时间点，与当前时间点相减，得到一个时间间隔 T。这个时间间隔 T 就是，从当前时间开始，需要等待多久，才会有第一个任务需要被执行。这样，定时器就可以设定在 T 秒之后，再来执行任务。从当前时间点到（T-1）秒这段时间里，定时器都不需要做任何事情。

当 T 秒时间过去之后，定时器取优先级队列中队首的任务执行。然后再计算新的队首任务的执行时间点与当前时间点的差值，把这个值作为定时器执行下一个任务需要等待的时间。

这样，定时器既不用间隔 1 秒就轮询一次，也不用遍历整个任务列表，性能也就提高了。

3.2 利用堆求 Top K

我们可以把这种求 Top K 的问题抽象成两类。一类是针对静态数据集合，也就是说数据集合事先确定，不会再变。另一类是针对动态数据集合，也就是说数据集合事先并不确定，有数据动态地加入到集合中。

针对静态数据，如何在一个包含 n 个数据的数组中，查找前 K 大数据呢？我们可以维护一个大小为 K 的小顶堆，顺序遍历数组，从数组中取出数据与堆顶元素比较。如果比堆顶元素大，我们就把堆顶元素删除，并且将这个元素插入到堆中；如果比堆顶元素小，则不做处理，继续遍历数组。这样等数组中的数据都遍历完之后，堆中的数据就是前 K 大数据了。

遍历数组需要 O(n) 的时间复杂度，一次堆化操作需要 O(logK) 的时间复杂度，所以最坏情况下，n 个元素都入堆一次，时间复杂度就是 O(nlogK)。

针对动态数据求得 Top K 就是实时 Top K。怎么理解呢？举个例子，一个数据集合中有两个操作，一个是添加数据，另一个询问当前的前 K 大数据。如果每次询问前 K 大数据，我们都基于当前的数据重新计算的话，那时间复杂度就是 O(nlogK)，n 表示当前的数据的大小。

实际上，我们可以一直都维护一个 K 大小的小顶堆，当有数据被添加到集合中时，我们就拿它与堆顶的元素对比。如果比堆顶元素大，我们就把堆顶元素删除，并且将这个元素插入到堆中；如果比堆顶元素小，则不做处理。这样，无论任何时候需要查询当前的前 K 大数据，我们都可以立刻返回给他。

3.3 利用堆求中位数

中位数，顾名思义，就是处在中间位置的那个数。如果数据的个数是奇数，把数据从小到大排列，那第 n/2 ​+ 1 个数据就是中位数（假设数据是从 0 开始编号的）；如果数据的个数是偶数的话，那处于中间位置的数据有两个，第 n / 2​ 个和第 n/2 ​+ 1 个数据，这个时候，我们可以随意取一个作为中位数，比如取两个数中靠前的那个，就是第 n/2​ 个数据。

对于一组静态数据，中位数是固定的，我们可以先排序，第 n/2​ 个数据就是中位数。每次询问中位数的时候，我们直接返回这个固定的值就好了。所以，尽管排序的代价比较大，但是边际成本会很小。但是，如果我们面对的是动态数据集合，中位数在不停地变动，如果再用先排序的方法，每次询问中位数的时候，都要先进行排序，那效率就不高了。

借助堆这种数据结构，我们不用排序，就可以非常高效地实现求中位数操作。我们来看看，它是如何做到的？

我们需要维护两个堆，一个大顶堆，一个小顶堆。大顶堆中存储前半部分数据，小顶堆中存储后半部分数据，且小顶堆中的数据都大于大顶堆中的数据。

也就是说，如果有 n 个数据，n 是偶数，我们从小到大排序，那前 n/2​ 个数据存储在大顶堆中，后 n/2​ 个数据存储在小顶堆中。这样，大顶堆中的堆顶元素就是我们要找的中位数。如果 n 是奇数，情况是类似的，大顶堆就存储 n/2 ​+ 1 个数据，小顶堆中就存储 n/2​ 个数据。
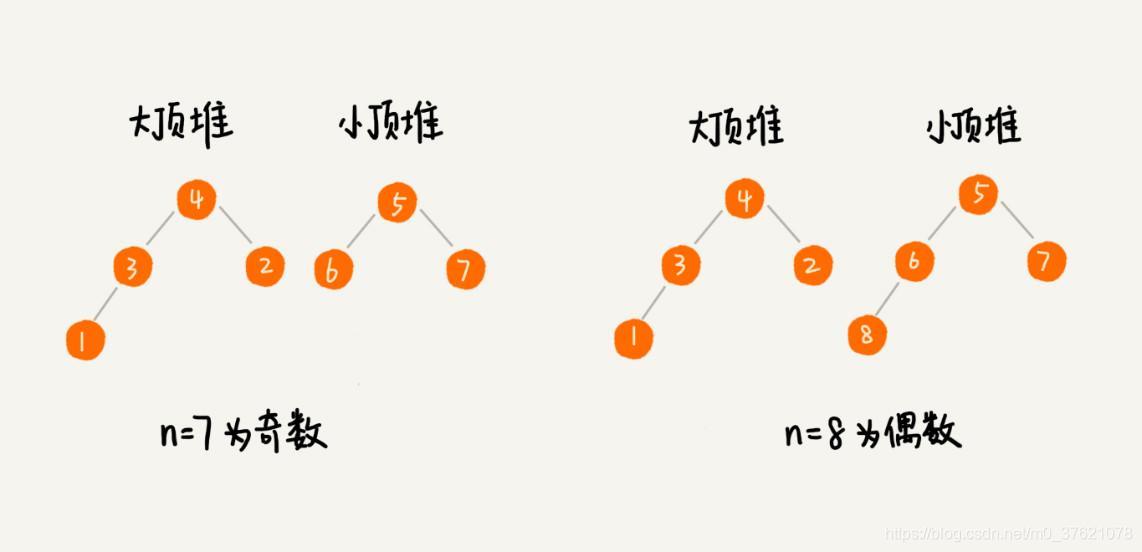
大顶堆与小顶堆求中位数
我们前面也提到，数据是动态变化的，当新添加一个数据的时候，我们如何调整两个堆，让大顶堆中的堆顶元素继续是中位数呢？如果新加入的数据小于等于大顶堆的堆顶元素，我们就将这个新数据插入到大顶堆；否则，我们就将这个新数据插入到小顶堆。

这个时候就有可能出现，两个堆中的数据个数不符合前面约定的情况：如果 n 是偶数，两个堆中的数据个数都是 n/2​；如果 n 是奇数，大顶堆有 n/2 ​+ 1 个数据，小顶堆有 n/2​ 个数据。这个时候，我们可以从一个堆中不停地将堆顶元素移动到另一个堆，通过这样的调整，来让两个堆中的数据满足上面的约定。
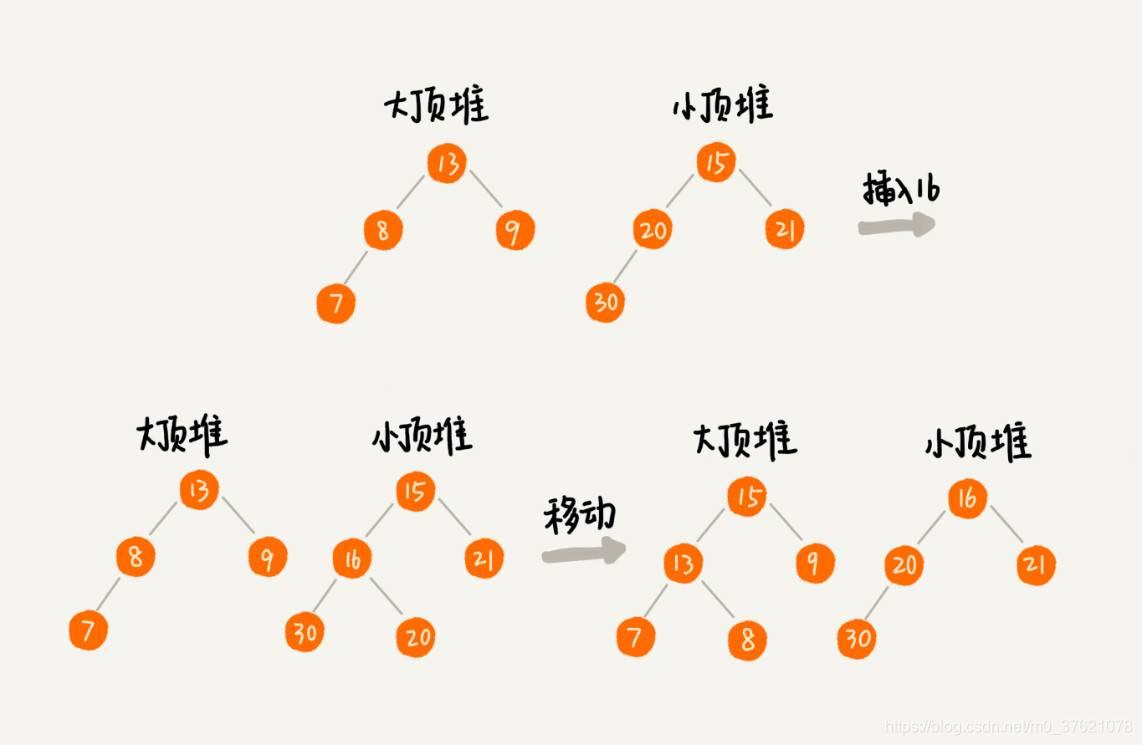
大顶堆与小顶堆元素插入与移动
于是，我们就可以利用两个堆，一个大顶堆、一个小顶堆，实现在动态数据集合中求中位数的操作。插入数据因为需要涉及堆化，所以时间复杂度变成了 O(logn)，但是求中位数我们只需要返回大顶堆的堆顶元素就可以了，所以时间复杂度就是 O(1)。

  • 利用堆求其它百分位数

实际上，利用两个堆不仅可以快速求出中位数，还可以快速求其它百分位的数据，原理是类似的。比如，“如何快速求服务的 99% 响应时间？”，这里先解释下，什么是“百分位数”和“99%响应时间”。

如果有 n 个数据，将数据从小到大排列之后，99 百分位数大约就是第 n * 99% 个数据，同类，80 百分位数大约就是第 n * 80% 个数据。再来看 99% 响应时间，如果有 100 个服务访问请求，每个服务请求的响应时间都不同，比如 55 毫秒、100 毫秒、23 毫秒等，我们把这 100 个服务的响应时间按照从小到大排列，排在第 99 的那个数据就是 99% 响应时间，也叫 99 百分位响应时间。

弄懂了这些概念，我们再来看如何求 99% 响应时间。我们维护两个堆，一个大顶堆，一个小顶堆。假设当前总数据的个数是 n，大顶堆中保存 n * 99% 个数据，小顶堆中保存 n * 1% 个数据，大顶堆堆顶的数据就是我们要找的 99% 响应时间。

每次插入一个数据的时候，我们要判断这个数据跟大顶堆和小顶堆堆顶数据的大小关系，然后决定插入到哪个堆中。如果这个新插入的数据比大顶堆的堆顶数据小，那就插入大顶堆；如果这个新插入的数据比小顶堆的堆顶数据大，那就插入小顶堆。

但是，为了保持大顶堆中的数据占 99%，小顶堆中的数据占 1%，在每次新插入数据之后，我们都要重新计算，这个时候大顶堆和小顶堆中的数据个数，是否还符合 99:1 这个比例。如果不符合，我们就将一个堆中的数据移动到另一个堆，直到满足这个比例。移动的方法类似前面求中位数的方法，这里就不啰嗦了。

通过这样的方法，每次插入数据，可能会涉及几个数据的堆化操作，所以时间复杂度是 O(logn)。每次求 99% 响应时间的时候，直接返回大顶堆中的堆顶数据即可，时间复杂度是 O(1)。

本章数据结构实现源码下载地址：https://github.com/StreamAI/ADT-and-Algorithm-in-C/tree/master/datastruct

更多文章：

注：本文转载自blog.csdn.net的流云IoT的文章"https://blog.csdn.net/m0_37621078/article/details/103937939"。版权归原作者所有，此博客不拥有其著作权，亦不承担相应法律责任。如有侵权，请联系我们删除。
复制链接
相关推荐
发表评论

评论记录：

未查询到任何数据！