数据结构与算法分析（三）--- 队列、栈的实现与应用

文章目录

一、队列的实现

想要理解队列很简单，因为它的性质和我们日常生活中的排队很类似，线性、先到先处理、后到排末尾。很显然，队列也是一种线性表，但比线性表的要求更严格，线性表可以对中间的元素进行访问和操作，队列则只能从首尾两端访问或操作元素，队列是一种操作受限的线性表，队列的所有特性都可以由线性表实现。

可能你会疑惑：既然链表、数组、游标数组都可以实现队列的所有特性，我们为何还要为队列单独实现一种数据结构呢？从功能上来说，数组或链表确实可以代替队列，但你要知道，特定的数据结构是对特定场景的抽象。而且，数组或链表暴露了太多的操作接口，操作上的确灵活自由，但使用时就比较不可控，自然也就更容易出错。为队列专门实现一个数据结构，可以限制对队列的操作，保证其”先到先处理、后到排末尾“的规矩。
队列模型
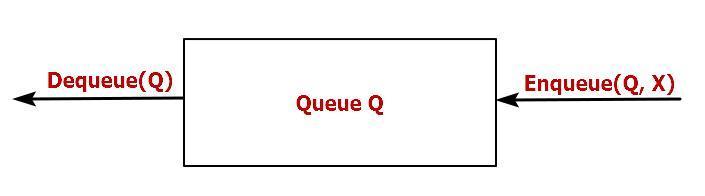
队列作为一种符合”先进先出（FIFO—first in first out）“特性的数据结构，应用非常广泛，特别是一些具有额外特性的队列，比如循环队列、阻塞队列、并发队列，它们在很多偏底层系统、框架、中间件的开发中，起着关键的作用，比如环形缓存就用到了循环队列。

队列作为一种操作受限的线性表，完全可以由任意一种线性表来实现，顺序表实现的队列称为顺序队列，链式表实现的队列称为链式队列。由于队列只有入队enqueue()、出队dequeue()两个操作，不需要随机访问，所以顺序队列与链式队列的选择，主要考虑队列容量的可扩展性，假如队列容量大小预期变化不大，可以使用数组实现队列；假如队列容量在后期不断增加，则可以使用链表实现队列，当然也可以使用变长数组实现，C++ STL队列容器就是使用双向变长数组deque实现的。

1.1 顺序队列的实现

前面介绍顺序表时提到，数组随机访问效率比较高，插入、删除元素需要涉及其后元素的搬移操作，因此效率较低。队列需要的两种操作：队尾入队、队首出队，实际上就是元素的尾部插入与首部删除，数组删除首部元素需要后面的所有元素全部向前搬移一个位置，会导致数组实现的队列出队效率很低。

既然顺序队列出队效率低的原因是元素搬移操作，我们能否让存储单元不动，借鉴游标数组的技巧，分别使用一个队首游标与队尾游标来实现队列呢？就好像早期的工厂流水线，机器或零部件不动，工人移动，完成组装焊接等操作，比来回搬移机器零部件效率提升了不少。

使用队首与队尾游标完成入队与出队操作，确实能省去元素搬移的操作，提高效率。但细想后发现，伴随着入队、出队操作，队尾与队首游标会不断后移，数组的地址空间是有限的，当队尾游标移动到数组的末尾后，就没法继续插入新元素了，如果数组中还有空位置，就需要想办法重新利用这些空位置。怎么重复利用已从队首取出元素留下的空位置呢？

按照线性思维，很容易想到，当队尾游标移动到数组末尾后，把队首游标到队尾游标之间的元素（也即队列中的有效元素）全部搬移到数组最前面，不就能重新利用前面已被队列使用过的空位置吗？就像下面图示的：
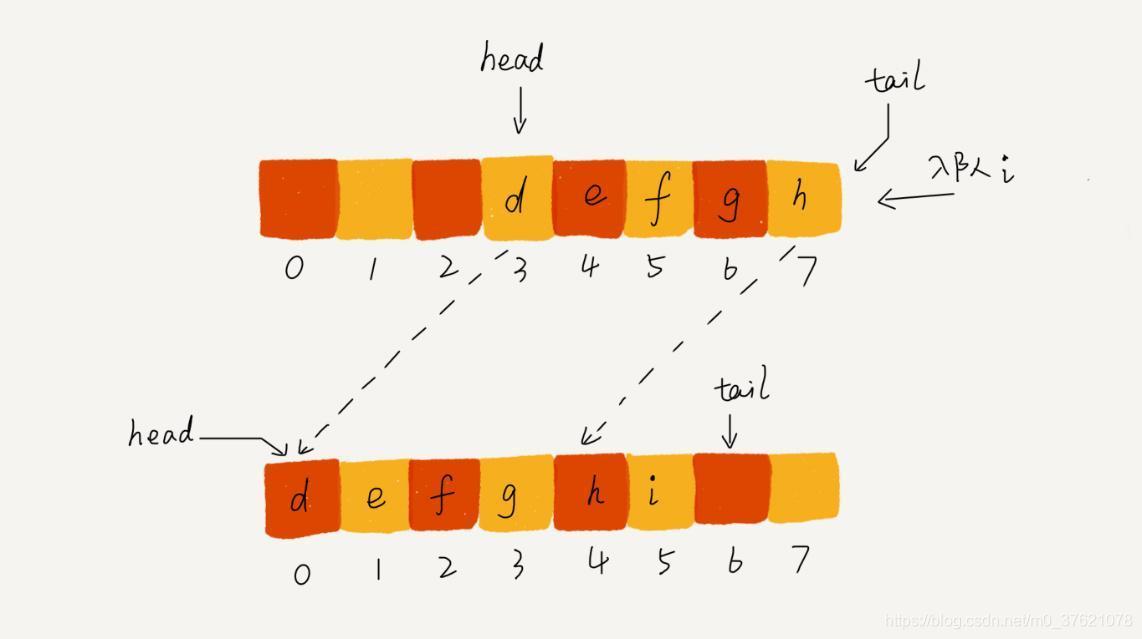
顺序队列满时元素搬移
上面的方法虽说比每次出队都搬移元素的效率高了不少，每当队尾游标到末尾时才整体搬移一次全部队列元素，但还是免不了搬移元素导致的效率降低。有没有什么方法能避免元素的搬移呢？

回想下前面介绍的循环链表，既然链表可以实现循环访问，游标数组自然也可以模拟循环链表的特性。当队尾游标后移到数组末尾时，让其重新移回到数组起始位置不就可以实现循环访问了吗，毕竟游标也是显式存储的元素间指向关系。

实现循环访问的队列称为循环队列，循环队列既可以通过循环链表实现，也可以通过循环游标数组实现。循环队列的逻辑结构图示如下（为了更形象，以环形展示）：
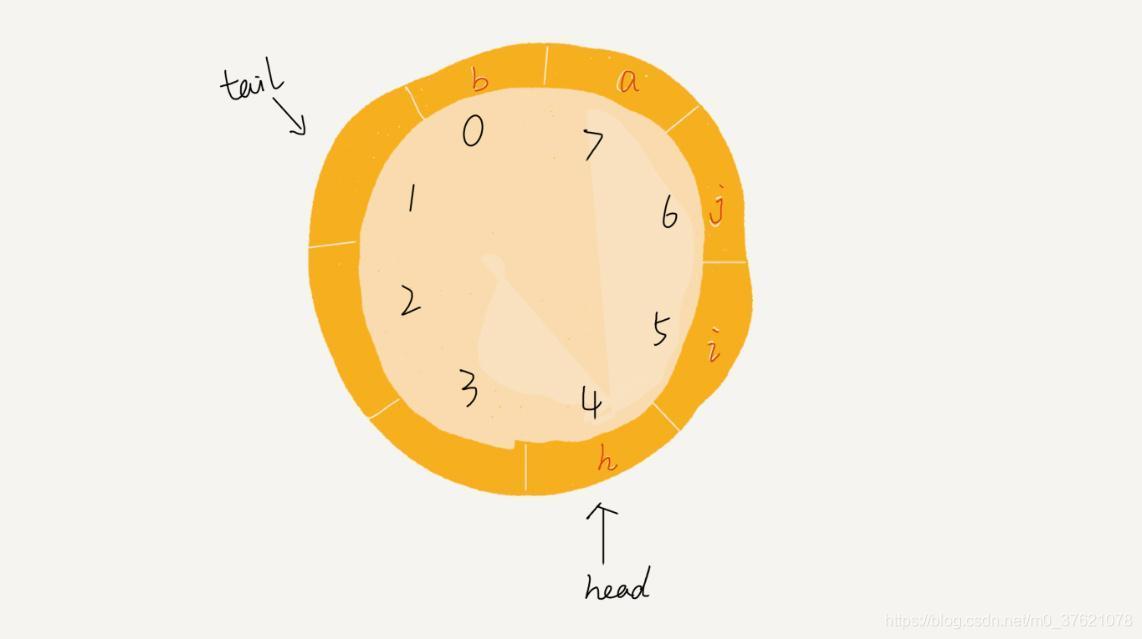
循环队列逻辑结构
循环队列就可以很好的避免数据搬移操作，效率比着前两种方案能提升很多。接下来看看循环队列如何实现？

循环队列的入队和出队操作比较简单，入队时只需要只需要将数据保存到队尾游标指向的存储单元，并将队尾游标后移一位即可；出队时只需要将队首游标指向的存储单元中的数据取出，并将队首游标后移一位即可。对于线性表来说，最重要的问题是防止访问越界，对于循环队列来说，最重要的问题则是确定队列为空和队列已满的判定条件。

队列为空比较好判断，队首与队尾游标指向同一个存储单元即表示队列为空。队列已满的判断条件在非循环队列中是队尾游标到数组末尾边界了，对于循环队列来说如何判定呢？下面先看一个循环队列已满的状态图示：
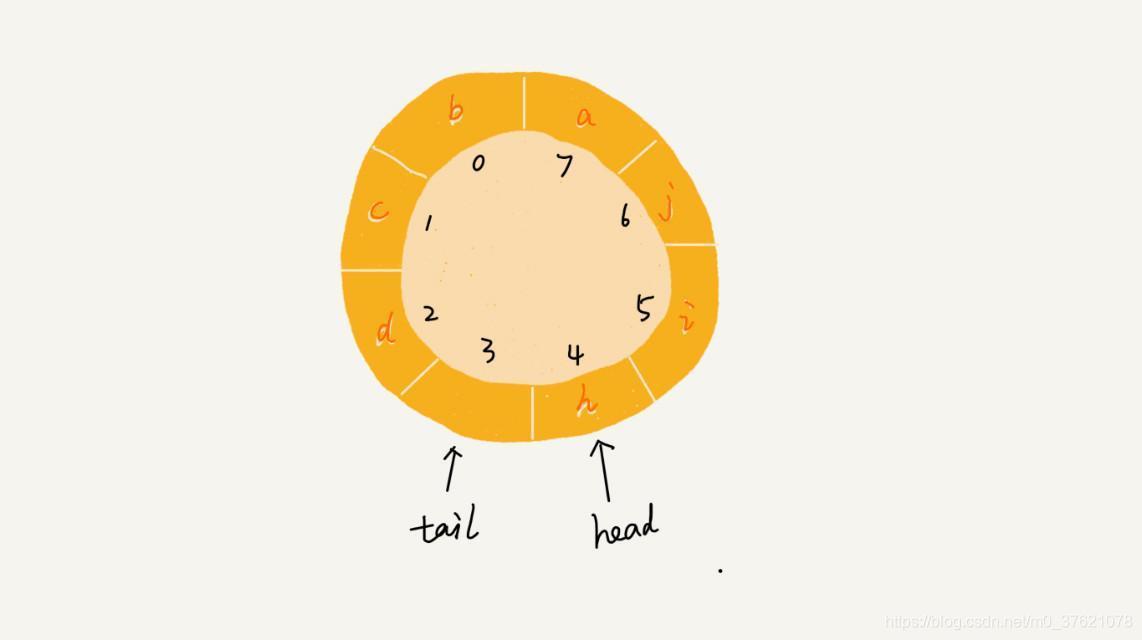
循环队列已满状态
从上面的循环队列已满状态图可以看出，循环队列已满时队尾游标指向的位置实际上并没有存储数据，循环队列会浪费一个数组的存储空间。当队列已满时，按照游标增长方向，队尾指针后移一位会与队首指针重合，这个可以看作循环队列已满的判定条件（也即tail + 1 = head）。但循环队列到末尾后，每次重新让其指向首部比较麻烦，既然涉及到循环，我们很容易想到取模运算，假设数组大小为n，则循环队列已满的判定条件就是(tail + 1)%n = head。

由于循环队列的队首游标与队尾游标处于变化中，我们需要经常访问队首与队尾游标，那么如何能快速访问该循环队列的队首与队尾游标呢？回顾下之前介绍单向链表时，使用了一个额外的链表头，不存放用户数据信息，只存放该链表的统计信息，包括链表内元素数目、指向首结点的指针、指向尾结点的指针等信息。我们可以借鉴这种技巧，也为循环队列提供一个队列头，用于存储该循环队列的队首游标、队尾游标、队列中有效元素数量、顺序表首地址、顺序表容量等信息，这些信息可以封装在一个结构体内，封装示例如下：

// datastruct\queue.c

struct QueueHead{
    int capacity;
    int haed;
    int tail;
    int size;
    ElementType *Array;
};
typedef struct QueueHead *Queue;

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 循环队列创建与销毁

有了循环队列头，要想执行入队、出队操作，需要先创建循环队列，循环队列的创建与删除函数实现代码如下：

// datastruct\queue.c

Queue Create(int capacity)
{
    Queue Q = malloc(sizeof(struct QueueHead));
    if(Q == NULL)
    {
    	printf("Out of space!");
    	return NULL;
    }

    Q->Array = malloc(capacity * sizeof(ElementType));
    if(Q->Array == NULL)
        printf("Out of space!");

    Q->capacity = capacity;
    Q->head = 0;
    Q->tail = 0;
    Q->size = 0;

    return Q;
}

void Destroy(Queue Q)
{
    free(Q->Array);
    free(Q);
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 循环队列入队与出队：

有了上面的循环队列为空、已满的判定条件，实现其入队与出队函数就简单了，实现代码如下：

// datastruct\queue.c

bool Enqueue(Queue Q, ElementType x)
{
    if((Q->tail + 1)%Q->capacity == Q->head)
        return false;
    
    Q->Array[Q->tail] = x;
    Q->tail = (Q->tail + 1) % Q->capacity;
    Q->size++;

    return true;
}

ElementType Dequeue(Queue Q)
{
    if(Q->head == Q->tail)
        return (ElementType)NULL;

    ElementType ret = Q->Array[Q->head];
    Q->head = (Q->head + 1) % Q->capacity;
    Q->size--;

    return ret;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25

接下来给出一个循环队列操作的示例程序，为了更直观，实现了一个打印循环队列中所有有效元素的函数。上面出队的实现代码并不严谨，当队列为空时，假如ElementType为int，将返回0，我们无法判定返回的是队列已空还是队首元素值0（这个问题可以通过返回元素值地址的方式解决，返回NULL则表示队列已空，因为元素值地址不为NULL）。我们在操作循环队列时，最好养成入队与出队前，先判断队列是否已满或为空再继续操作。示例程序代码如下：

//datastruct\queue.c

#include 
#include 
#include 

#define ElementType int

struct QueueHead{
    int capacity;
    int head;
    int tail;
    int size;
    ElementType *Array;
};
typedef struct QueueHead *Queue;

Queue Create(int capacity);
bool Enqueue(Queue Q, ElementType x);
ElementType Dequeue(Queue Q);
void Destroy(Queue Q);

void printQueue(Queue Q)
{
    printf("Queue has %d elements: ", Q->size);
    int i = Q->head;
    while(i != Q->tail)
    {
        if(i != Q->head)
            printf(" ");
        printf("%d", Q->Array[i]);
        i = (i + 1) % Q->capacity;
    }
    printf("\n\n");
}

int main(void)
{
    Queue Q = Create(100);

    for(int i = 1; i < 9; i++)
    {
        if(Enqueue(Q, i * i) == false)
        {
            printf("The queue is full.\n");
            break;
        }
    }
    printf("\n");
    printQueue(Q);

    for(int i = 1; i < 7; i++)
    {
        if(Q->size == 0)
        {
            printf("The queue is empty.\n");
            break;
        }
        printf("%d ", Dequeue(Q));
    }
    printf("\n");
    printQueue(Q);

    Destroy(Q);

    return 0;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59
  • 60
  • 61
  • 62
  • 63
  • 64
  • 65
  • 66
  • 67

上述示例程序的执行结果如下：
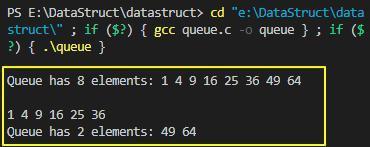
循环队列示例程序执行结果

1.2 链式队列的实现

使用链表不需要元素搬移，也不需要维持一个循环链表，入队时将新元素插入链表尾部，出队时移除链表首节点，并将链表原首结点的元素值返回即可。

单向链表在链表头尾部插入、删除元素比较高效，在链表末尾插入元素需要先遍历链表，假如链表元素很多就会很低效。怎么提高在链表尾部插入新结点的效率呢？

还记得前面介绍单向链表时，链表头用于保存链表的统计信息，比如链表中元素数量、指向首结点的指针外，如果需要频繁在链表尾部插入元素，可以在链表头中再增加一个指向链表尾结点的指针，这样就可以省去每次的遍历操作，直接找到链表尾结点，将新元素插入其后面，再更新指向尾结点的指针即可。

按照上面的逻辑，我们使用单向链表实现队列就比较简单了，先看链表头和队列结点的数据封装结构：

// datastruct\queue_list.c

//QueueNode是普通结点,pNode是指向普通结点的指针
struct QueueNode{
    struct QueueNode *next;
    ElementType Element;
};
typedef struct QueueNode *pNode;

//QueueHead是队列头结点,Queue是指向队列头的指针
struct QueueHead{
    struct QueueNode *head;
    struct QueueNode *tail;
    int size;
};
typedef struct QueueHead *Queue;

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16

接下来给出链式队列的创建、入队、出队函数的实现代码（链式队列销毁比较简单，这里不再单独封装接口了）：

// datastruct\queue_list.c

Queue Create(void)
{
    Queue Q = malloc(sizeof(struct QueueHead));

    if(Q == NULL)
    {
    	printf("Out of space!");
    	return NULL;
    }
    
    Q->head = NULL;
    Q->tail = NULL;
    Q->size = 0;

    return Q;
}

void Enqueue(Queue Q, ElementType x)
{
    pNode pTemp = malloc(sizeof(struct QueueNode));
    if(pTemp == NULL)
        printf("Out of space!");
    else
    {
        pTemp->Element = x;
        pTemp->next = NULL;
    
        if(Q->size == 0)
        {
            Q->head = pTemp;
            Q->tail = pTemp;
        }else{
            Q->tail->next = pTemp;
            Q->tail = pTemp;
        }    
        Q->size++;
    }
}

ElementType Dequeue(Queue Q)
{
    if(Q->head == NULL)
        return (ElementType)NULL;

    ElementType ret = Q->head->Element;
    pNode pTemp = Q->head;
    Q->head = pTemp->next;

    Q->size--;
    free(pTemp);

    return ret;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55

给出操作链式队列的一个示例代码如下：

// datastruct\queue_list.c

#include 
#include 
#include 

#define ElementType int

//QueueNode是普通结点,pNode是指向普通结点的指针
struct QueueNode{
    struct QueueNode *next;
    ElementType Element;
};
typedef struct QueueNode *pNode;

//QueueHead是队列头结点,Queue是指向队列头的指针
struct QueueHead{
    struct QueueNode *head;
    struct QueueNode *tail;
    int size;
};
typedef struct QueueHead *Queue;

Queue Create(void);
void Enqueue(Queue Q, ElementType x);
ElementType Dequeue(Queue Q);

void printQueue(Queue Q)
{
    pNode ptr = Q->head;

    printf("List has %d elements: ", Q->size);
    while(ptr != NULL)
    {
        if(ptr != Q->head)
            printf(" --> ");

        printf("%d", ptr->Element);
        ptr = ptr->next;
    }
    printf("\n");
}

int main(void)
{
    int i;

    Queue Q = Create();

    for(i = 1; i < 9; i++)
        Enqueue(Q, i * i);
    printf("\n");
    printQueue(Q);

    for(i = 1; i < 7; i++)
    {
        if(Q->size == 0)
        {
            printf("The queue is empty.\n");
            break;
        }
        printf("%d ", Dequeue(Q));
    }
    printf("\n");
    printQueue(Q);

    free(Q);

    return 0;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59
  • 60
  • 61
  • 62
  • 63
  • 64
  • 65
  • 66
  • 67
  • 68
  • 69
  • 70

上面链式队列的示例程序执行结果如下：
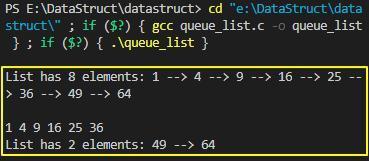
链式队列示例程序执行结果

二、栈的实现

有了符合”先进先出（FIFO—first in first out）“特性的队列，有没有符合相反特性”后进先出（LIFO—last in first out）“的数据结构呢？还记得线性表中的游标数组用于管理空闲存储单元的freelist吗？它就符合”后进先出“的特性，而且符合这种特性的操作在计算机中很常见，因此也有必要为其专门实现一个数据结构：栈。

要理解栈也不难，小时候玩过玩具枪或者看过枪战片的话，应该对弹匣中子弹的装载与弹出顺序有印象，弹匣只有一个子弹出入口，弹匣中有弹簧和卡子，我们最先装填进弹匣的子弹（可称为”入栈“或”压栈“）最后从弹匣中弹出（可称为”出栈“或”弹栈“），可谓是”先到进栈底，后到压上头“。
栈模型
栈同样是一种操作受限的线性表，为何专门为栈实现一个数据结构呢？跟队列类似，同样是为了隐藏不需要的接口，保证栈这种”先到进栈底，后到压上头“的规矩不被破坏。

栈作为一个比较基础的数据结构，应用场景同样相当广泛，比如操作系统在涉及函数嵌套调用或嵌套中断时，就需要使用栈这种符合”后进先出“特性的结构来保证嵌套返回的正确顺序；再比如成对出现的大、中、小括号的匹配检查，使用栈这种数据结构也更加方便。

栈作为一种操作受限的线性表，也是可以由任意一种线性表来实现的，顺序表实现的栈称为顺序栈，链式表实现的栈称为链式栈。由于栈只有压栈push()、弹栈pop()两个操作，不需要随机访问，所以顺序栈与链式栈的选择类似队列，也是主要考虑栈容量的可扩展性。当然也可以使用变长数组实现，C++ STL栈容器就是使用双向变长数组deque实现的。

2.1 顺序栈的实现

栈只是在栈顶插入或删除元素，比队列更简单，假如用游标数组来实现栈，不需要操作首部元素，因此不需要考虑数组元素搬移的问题，也没必要使用类型循环队列的技巧了。

栈只需要一个栈顶游标，我们同样使用一个栈头来保存栈的一些统计信息，比如指向栈顶元素的游标、栈的容量、栈中元素数量等信息。栈头结构可以封装如下：

// datastruct\stack.c

struct StackHead{
    int capacity;
    int TopOfStack;
    int size;
    ElementType *Array;
};
typedef struct StackHead *Stack;

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 栈的创建与销毁
// datastruct\stack.c

Stack Create(int capacity)
{
    Stack S = malloc(sizeof(struct StackHead));
    if(S == NULL)
    {
    	printf("Out of space!");
    	return NULL;
    }

    S->Array = malloc(capacity * sizeof(ElementType));
    if(S->Array == NULL)
        printf("Out of space!");

    S->capacity = capacity;
    S->TopOfStack = 0;
    S->size = 0;

    return S;
}

void Destroy(Stack S)
{
    free(S->Array);
    free(S);
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 栈的压入与弹出
// datastruct\stack.c

bool Push(Stack S, ElementType x)
{
    if(S->size == S->capacity)
        return false;
    
    S->Array[S->TopOfStack] = x;
    S->TopOfStack++;
    S->size++;

    return true;
}

ElementType Pop(Stack S)
{
    if(S->size == 0)
        return (ElementType)NULL;

    ElementType ret = S->Array[S->TopOfStack - 1];
    S->TopOfStack--;
    S->size--;

    return ret;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25

栈的实现比较简单，下面给出一个示例程序：

// datastruct\stack.c

#include 
#include 
#include 

#define ElementType int

struct StackHead{
    int capacity;
    int TopOfStack;
    int size;
    ElementType *Array;
};
typedef struct StackHead *Stack;

Stack Create(int capacity);
bool Push(Stack S, ElementType x);
ElementType Pop(Stack S);
void Destroy(Stack S);

int main(void)
{
    int i;

    Stack S = Create(100);

    for(i = 1; i < 9; i++)
    {
        if(Push(S, i * i) == false)
        {
            printf("The stack is full.\n");
            break;
        }
        printf("%d ", i * i);
    }
    printf("\n");

    for(i = 1; i < 9; i++)
    {
        if(S->size == 0)
        {
            printf("The stack is empty.\n");
            break;
        }
        printf("%d ", Pop(S));
    }
    printf("\n");

    Destroy(S);

    return 0;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53

栈的示例程序执行结果如下：
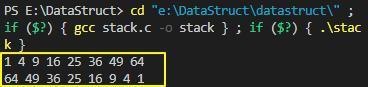
顺序栈示例程序执行结果

2.2 链式栈的实现

链式栈的实现也很简单，只需要把单向链表的首结点作为栈顶即可，往连表头后（也即首结点前）插入新元素即为入栈，移除首结点即为出栈。

链式栈同样使用一个链表头记录统计信息，包括执行栈顶的指针、栈内元素数量等，链式栈的链表头与栈结点的数据封装结构如下：

// datastruct\stack_list.c

//StackNode是普通结点,pNode是指向普通结点的指针
struct StackNode{
    struct StackNode *next;
    ElementType Element;
};
typedef struct StackNode *pNode;

//StackHead是队列头结点,Stack是指向队列头的指针
struct StackHead{
    struct StackNode *top;
    int size;
};
typedef struct StackHead *Stack;

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15

链式栈的创建、入栈、出栈函数实现比较简单，相当于单向链表只能在链表头后插入或移除元素，实现代码如下：

// datastruct\stack_list.c

Stack Create(void)
{
    Stack S = malloc(sizeof(struct StackHead));

    if(S == NULL)
    {
    	printf("Out of space!");
    	return NULL;
    }
    
    S->top = NULL;
    S->size = 0;

    return S;
}

void Push(Stack S, ElementType x)
{
    pNode pTemp = malloc(sizeof(struct StackNode));
    if(pTemp == NULL)
        printf("Out of space!");
    else
    {
        pTemp->Element = x;

        pTemp->next = S->top;
        S->top = pTemp;
 
        S->size++;
    }
}

ElementType Pop(Stack S)
{
    if(S->size == 0)
        return (ElementType)NULL;

    ElementType ret = S->top->Element;
    pNode pTemp = S->top;
    S->top = pTemp->next;

    S->size--;
    free(pTemp);

    return ret;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48

给出一个示例程序代码用以验证链式栈操作函数的实现是否有问题：

// datastruct\stack_list.c

#include 
#include 
#include 

#define ElementType int

//StackNode是普通结点,pNode是指向普通结点的指针
struct StackNode{
    struct StackNode *next;
    ElementType Element;
};
typedef struct StackNode *pNode;

//StackHead是队列头结点,Stack是指向队列头的指针
struct StackHead{
    struct StackNode *top;
    int size;
};
typedef struct StackHead *Stack;

Stack Create(void);
void Push(Stack S, ElementType x);
ElementType Pop(Stack S);

int main(void)
{
    int i;

    Stack S = Create();

    for(i = 1; i < 9; i++)
    {
        Push(S, i * i);

        printf("%d ", i * i);
    }
    printf("\n");

    for(i = 1; i < 9; i++)
    {
        if(S->size == 0)
        {
            printf("The stack is empty.\n");
            break;
        }
        printf("%d ", Pop(S));
    }
    printf("\n");

    free(S);

    return 0;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55

链式栈示例程序的执行结果如下：
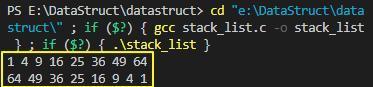
链式栈示例程序执行结果

三、队列与栈的STL容器

3.1 队列STL容器（C++11）

C++标准库当然也为队列这种常用的数据结构提供了STL容器： class queue<>，你可以使用push()将任意数量的元素放入queue中，也可以使用pop()将元素依其入队次序从容器中移除，由此可见，queue是一个典型的数据缓冲构造。
Queue接口
C++11 STL Queue的类模板定义如下（第一个参数T为元素类型，第二个参数Container定义queue内部用来存放元素的实际容器，默认采用deque）：

// 

namespace std{
	template <typename T,
			  typename Container = deque<T>>
	class queue;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7

由类模板定义可以看出，队列容器是对普通线性表容器的封装，隐藏了一些接口，只留下队列所需要的接口，以保证”先入先出“的特性。之所以默认选择deque作为底层实现容器，一方面是deque支持在首尾高效的插入、移除元素，另一方面deque移除元素会释放内存、扩容时不必在重分配时复制全部元素。

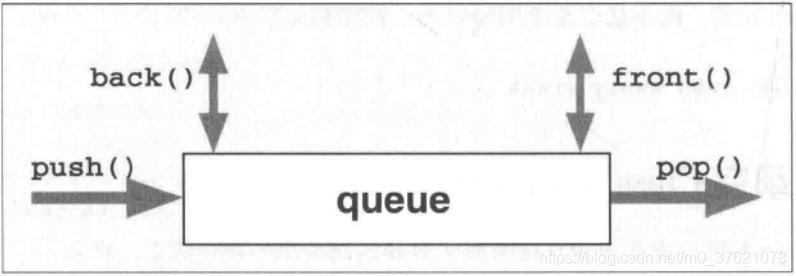
实际上queue容器只是很单纯的把各项操作转化为内部容器的对应调用，你可以使用任何线性表容器来实现queue，只要它们支持front()、back()、push_back()和pop_front()等操作，queue容器的内部接口如下：
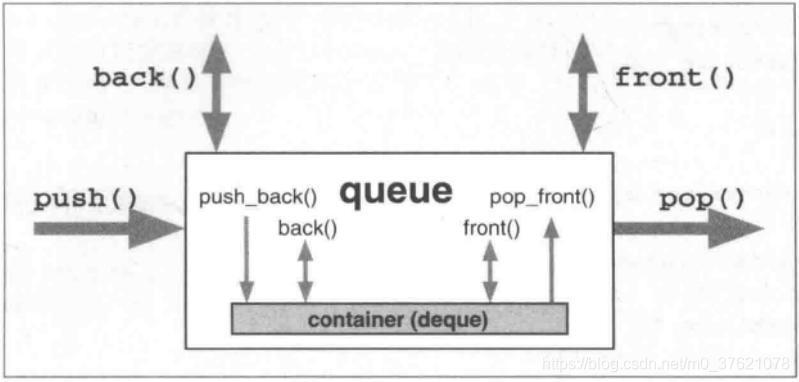
queue内部容器接口
从上图也可以看出，queue容器的核心接口也就四个（当然还有比如查询大小size()、判断是否为空empty()等辅助接口）：

  • push()：将一个元素放入queue中；
  • front()：返回queue内的下一个元素；
  • back()：返回queue内的最后一个元素；
  • pop()：从queue中移除一个元素。

下面给出一个queue应用示例程序供参考：

// datastruct\queue_demo.cpp

#include 
#include 
#include 

int main(void)
{
    std::queue<std::string> q;

    // insert three elements into the queue
    q.push("These ");
    q.push("are ");
    q.push("more than ");

    // read and print two elements from the queue
    std::cout << q.front();
    q.pop();
    std::cout << q.front();
    q.pop();

    // insert two new elements
    q.push("four ");
    q.push("words!");

    // skip one elements
    q.pop();

    // read and print two elements
    std::cout << q.front();
    q.pop();
    std::cout << q.front() << std::endl;
    q.pop();

    // print number of elements in the queue
    std::cout << "number of elements in the queue: " << q.size() << std::endl;

    return 0;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39

上面queue的示例代码运行结果如下（需要注意编译器是否支持C++11，比如g++在4.7以上版本才支持，添加-std=c++11即可）：
队列容器示例程序执行结果

3.2 栈STL容器（C++11）

C++标准库为栈实现的STL容器时：class stack<>，可以使用push()将任意数量的元素放入stack，也可以使用pop()将元素依其入栈的相反次序从容器中移除。
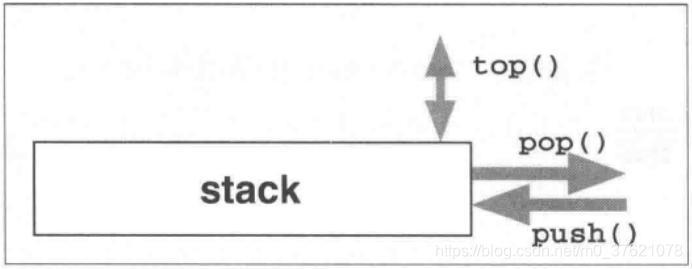
栈容器接口
C++11 STL Stack的类模板定义如下（第一个参数T为元素类型，第二个参数Container定义stack内部用来存放元素的实际容器，默认采用deque）：

// 

namespace std{
	template <typename T,
			  typename Container = deque<T>>
	class stack;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7

你可能会疑问，为什么栈容器默认使用deque而非vector实现呢？看起来vector单向变长数组已经能满足栈容器的需求且迭代器访问效率比deque更高，但vetor在扩容时需要复制全部元素，且在移除元素时不会主动释放内存，这些缺点导致C++标准库默认选择deque实现stack容器。如果预先对栈的使用容量有个初步估计，使用vector容器预留空间大一些，避免容器扩容，用vector实现stack就可以更高效了。

Stack容器的实现中只是很单纯的把各项操作转化为内部容器的对应调用，你可以使用任何线性表容器支持stack，只要它们提供以下成员函数：back()、push_back()、pop_back()，你只需要在创建stack对象时配置第二个参数Container即可。
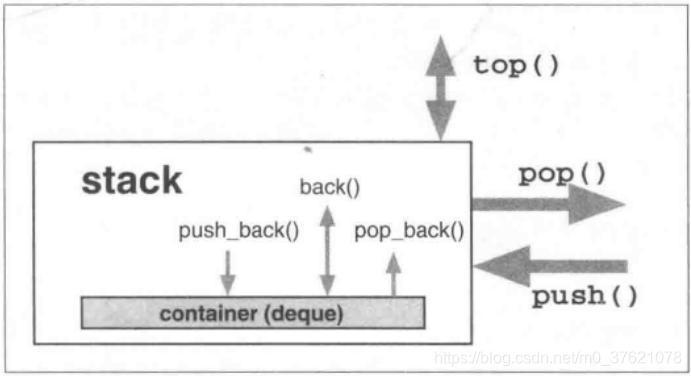
栈容器内部接口
从上图可以看出，stack栈的核心接口主要有三个（当然还有比如查询大小size()、判断是否为空empty()等辅助接口）：

  • push()：将一个元素压入stack内；
  • top()：返回stack内的栈顶元素；
  • pop()：从stack中弹出栈顶元素。

下面给出一个stack应用示例程序供参考：

// datastruct\stack_demo.cpp

#include 
#include 

int main(void)
{
    std::stack<int> st;

    // push three elements into the stack
    st.push(2);
    st.push(3);
    st.push(5);

    // pop and print two elements from the stack
    std::cout << st.top() << " ";
    st.pop();
    std::cout << st.top() << " ";
    st.pop();
    std::cout << std::endl;

    // modify top element;
    st.top() = 77;

    // push two new elements
    st.push(7);
    st.push(11);

    // pop one element without processing it
    st.pop();

    // pop and print remaining elements
    while (!st.empty())
    {
        std::cout << st.top() << " ";
        st.pop();
    }
    std::cout << std::endl;

    return 0;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41

上面stack的示例代码运行结果如下（需要注意编译器是否支持C++11，比如g++在4.7以上版本才支持，添加-std=c++11即可）：
栈容器示例程序执行结果

四、队列与栈的应用

4.1 阻塞队列与并发队列

队列这种数据结构比较基础，平时的业务开发不大可能从零实现一个队列，甚至都不会直接用到。而一些具有特殊特性的队列应用却比较广泛，比如阻塞队列和并发队列。

  • 阻塞队列

阻塞队列其实就是在队列基础上增加了阻塞操作。简单来说，就是在队列为空的时候，从队头取数据会被阻塞。因为此时还没有数据可取，直到队列中有了数据才能返回；如果队列已经满了，那么插入数据的操作就会被阻塞，直到队列中有空闲位置后再插入数据，然后再返回。

如果你了解多线程编程，不难发现，上述定义就是一个”生产者 - 消费者“模型，我们可以使用阻塞队列轻松实现一个”生产者 - 消费者“模型（可参考C++多线程并发之条件变量）：
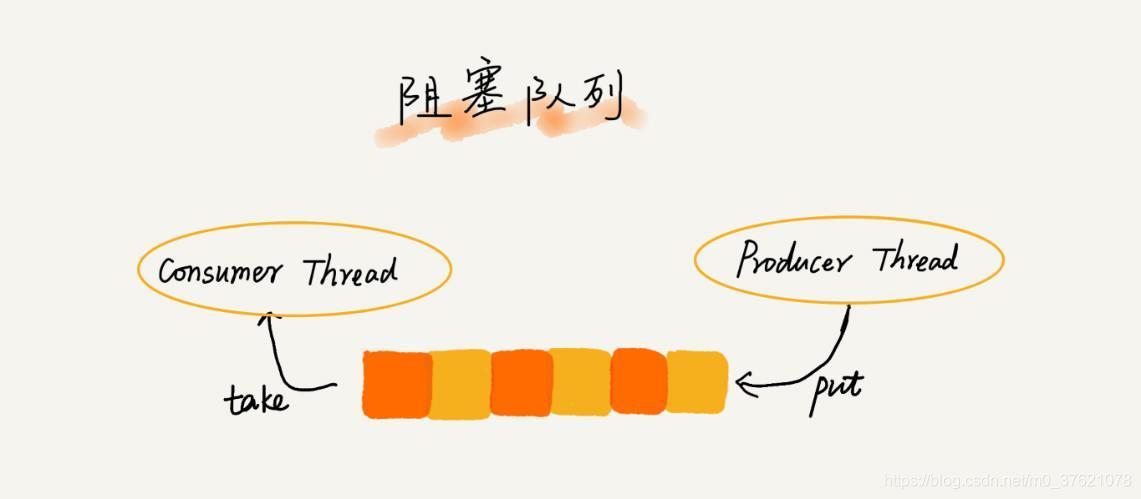
阻塞队列逻辑结构
这种基于阻塞队列实现的“生产者 - 消费者模型”，可以有效地协调生产和消费的速度。当“生产者”生产数据的速度过快，“消费者”来不及消费时，存储数据的队列很快就会满了。这个时候，生产者就阻塞等待，直到“消费者”消费了数据，“生产者”才会被唤醒继续“生产”。

而且不仅如此，基于阻塞队列，我们还可以通过协调“生产者”和“消费者”的个数，来提高数据的处理效率。比如前面的例子，我们可以多配置几个“消费者”，来应对一个“生产者”：
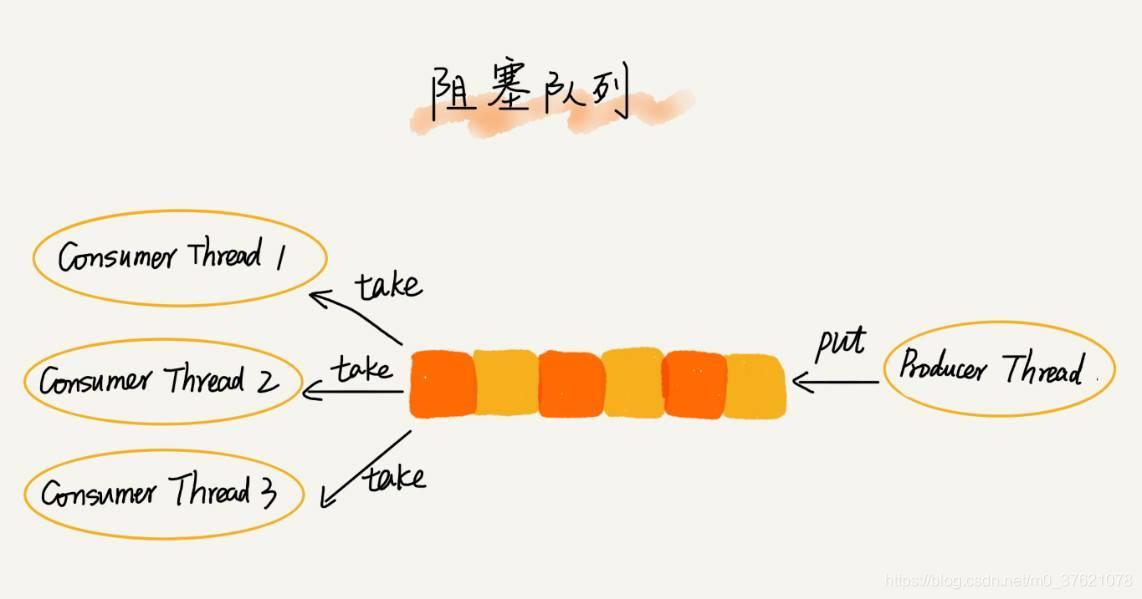
多消费者- 生产者模型

  • 并发队列

前面我们讲了阻塞队列，在多线程情况下，会有多个线程同时操作队列，这个时候就会存在线程安全问题，那如何实现一个线程安全的队列呢？

线程安全的队列我们叫作并发队列。最简单直接的实现方式是直接在 enqueue()、dequeue() 方法上加锁，但如果锁粒度较大，并发度会比较低，同一时刻仅允许一个存或者取操作。实际上，基于数组的循环队列，利用 CAS （Compare and Swap）原子操作（可参考C++多线程并发之原子操作与无锁编程），可以实现非常高效的并发队列，这也是循环队列比链式队列应用更加广泛的原因。

4.2 栈在括号匹配中的应用

我们编写C语言时，不同作用域的代码使用{}括起来，在表达式后或函数调用中使用()将操作数或参数括起来，在数组访问中使用[]将下标括起来，这些括号都要求左右匹配，编译程序会如何检查这些括号匹配是否正确呢？

我们尝试模拟编译器检查括号匹配的实现过程，假设表达式中允许三种括号：圆括号、方括号和大括号，并且它们可以任意嵌套，编写一个函数判断表达式中的各种左括号是否与右括号匹配。

左右括号匹配问题，一般涉及到嵌套，使用栈来解决比较方便。我们用栈来保存未匹配的左括号，从左到右依次扫描字符串。当扫描到左括号时，则将其压入栈中；当扫描到右括号时，从栈顶取出一个左括号。如果能够匹配，比如“(”跟“)”匹配，“[”跟“]”匹配，“{”跟“}”匹配，则继续扫描剩下的字符串。如果扫描的过程中，遇到不能配对的右括号，或者栈中没有数据，则说明为非法格式。

按照上述逻辑编写实现代码如下：

// datastruct\stack_demo.c

#include 
#include 
#include 

#define ElementType char
......
Stack Create(void);
void Push(Stack S, ElementType x);
ElementType Pop(Stack S);

bool BracketMatch(char str[])
{
    bool flag = true;
    int i;

    Stack S = Create();

    for(i = 0; str[i] != '\0' && flag == true; ++i)
    {
        switch (str[i])
        {
        case '(':
        case '[':
        case '{':
            Push(S, str[i]);
            break;
        case ')':
            if(S->size == 0 || Pop(S) != '(')
                flag = false;
            break;
        case ']':
            if(S->size == 0 || Pop(S) != '[')
                flag = false;
            break;
        case '}':
            if(S->size == 0 || Pop(S) != '{')
                flag = false;
            break;
        }
    }
    if(S->size == 0 && flag == true)
        return true;
    else
        return false;
}

int main(void)
{
	char str[100] = {0};

    printf("please input string:");
    scanf("%s", str);
    
    if(BracketMatch(str) == true)
        printf("Bracket match success.\n");
    else
        printf("Bracket match failed.\n");   

    return 0;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59
  • 60
  • 61
  • 62

上面示例程序的执行结果如下：
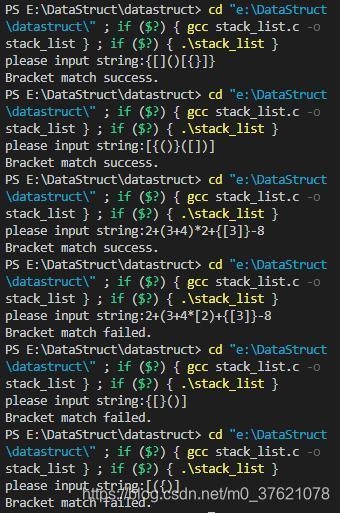
示例程序执行结果

4.3 栈在表达式求值中的应用

我们再来看栈的另一个常见的应用场景，编译器如何利用栈来实现表达式求值。为了方便解释，这里将算术表达式简化为只包含加减乘除四则运算，比如：34+13*9+44-12/3。对于这个四则运算，我们人脑可以很快求解出答案，但是对于计算机来说，理解这个表达式本身就是个挺难的事儿。如果换作你，让你来实现这样一个表达式求值的功能，你会怎么做呢？

实际上，编译器就是通过两个栈来实现的。其中一个保存操作数的栈，另一个是保存运算符的栈。我们从左向右遍历表达式，当遇到数字，我们就直接压入操作数栈；当遇到运算符，就与运算符栈的栈顶元素进行比较。

如果比运算符栈顶元素的优先级高，就将当前运算符压入栈；如果比运算符栈顶元素的优先级低或者相同，从运算符栈中取栈顶运算符，从操作数栈的栈顶取 2 个操作数，然后进行计算，再把计算完的结果压入操作数栈，继续比较。下面以 3+5*8-6 这个表达式为例，展示上述的计算过程；
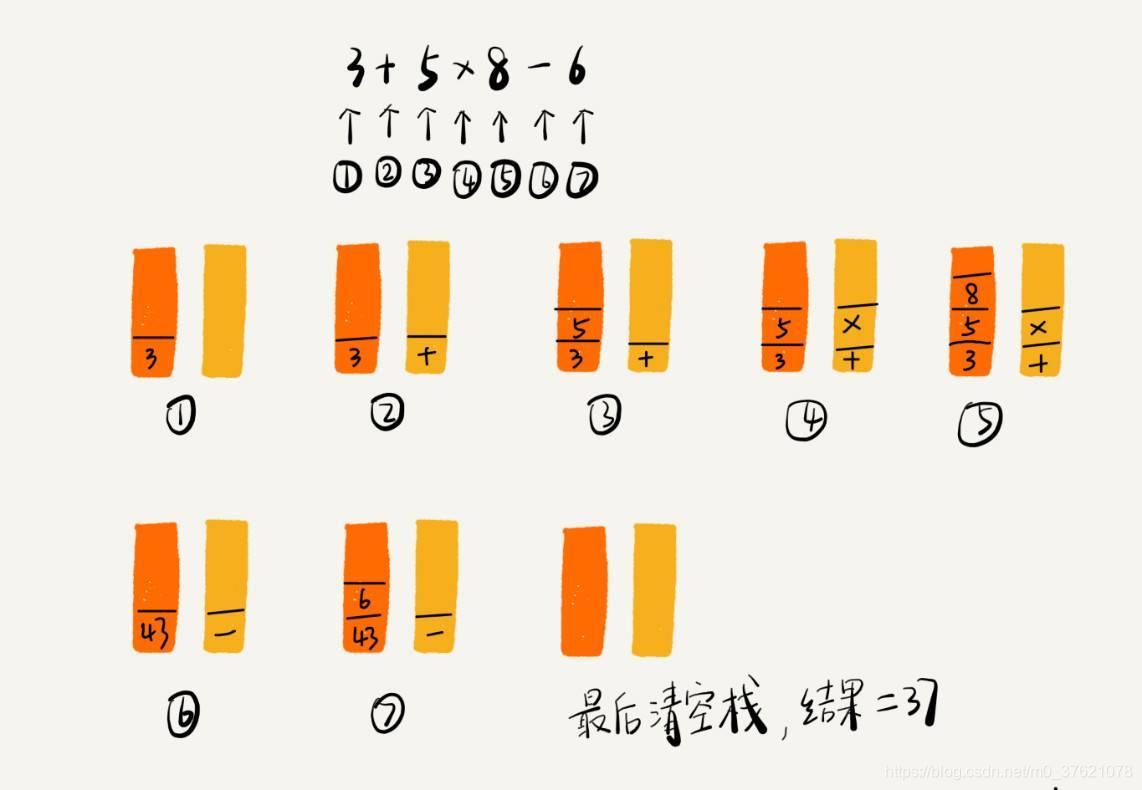
使用栈进行表达式求值过程图示
我们常见的表达式都有括号，假如表达式中有括号又该如何处理呢？括号属于运算符，因此增加括号对操作数栈的处理没有影响，对运算符栈的处理需要增加规则。由于括号的优先级比乘除优先级更高，当遇到左括号直接压入运算符栈；当遇到右括号，则从运算符栈中取栈顶运算符，从操作数栈的栈顶取 2 个操作数，然后进行计算，再把计算完的结果压入操作数栈，继续比较，直到运算符栈取出与之配对的左括号为止。

4.4 栈在函数调用中的应用

使用栈处理括号匹配的算法提供了一种实现函数调用的方法，多个括号可能涉及到嵌套，栈对处理多层嵌套的逻辑时比较有优势。

当操作系统调用一个新函数时，主调例程的所有局部变量需要由系统存储起来，否则被调用的新函数将会覆盖调用例程的变量。不仅如此，该主调例程的当前位置也必须要存储，以便在新函数运行完后知道向哪里转移或返回。当存在函数调用时，需要存储的所有重要信息均可作为一个栈帧入栈，当被调用函数执行完成，会将该函数对应的栈帧出栈。

在实际计算机中的栈常常是从内存分区的高端向下增长，而在许多系统中是不检测栈区溢出的。由于有太多同时运行着的函数，用尽栈空间的情况总是可能发生，特别是对递归的不当调用（比如递归复杂度过高或者递归深度过大等）。

在不进行栈溢出检测的语言或系统中，用尽栈空间可能会导致程序崩溃而没有明显的说明。在这些系统中，当你的栈太大时，可能会触及到你的数据部分（比如堆区），当你将一些信息写入数据部分时，这些信息将冲毁栈的信息，比如冲毁了返回地址，你的程序将返回到不确定的地址导致程序崩溃；假如栈触及到你的程序部分，可能会产生一些无意义的指令，并破坏原程序的指令，也会导致程序崩溃。

在编写程序时，需要注意不应该越出栈空间，特别需要注意对递归合理使用。比如下面一段递归代码：

int fibonacci_recursive(int n)
{
    if(n < 0)
        return 0;
    else if(n == 0 || n == 1)
        return 1;
    else
        return (fibonacci_recursive(n-1) + fibonacci_recursive(n-2));
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9

在博客：递推与递归中分析过，该斐波那契数列的递归求解涉及大量重复计算，导致其复杂度比较高，当递归深度略大时很容易导致栈溢出。我们可以将其优化为尾递归形式，使其当前调用层级的所有中间结果通过参数传递给下一调用层级，不必再保存当前栈帧，编译器就可以优化为重复使用当前栈帧，不至于使栈空间的使用过多。上面的代码优化为尾递归形式如下：

int fibonacci_Tailrecursive(int n, int res1, int res2)
{
    if(n < 0)
        return 0;
    else if(n == 0)
        return res1;
    else if(n == 1)
        return res2;
    else
        return fibonacci_Tailrecursive(n-1, res2, res2 + res1);
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11

但有些编译器不支持尾递归优化，或者默认没有开启尾递归优化，我们怎样将尾递归优化改为正常的函数调用，以免在不支持尾递归优化的编译器中出现栈溢出呢？

尾递归可以通过将递归调用变成goto语句并在其前加上对函数每个参数的赋值语句而手工消除。它模拟了递归调用，因为没有什么需要存储，在递归调用结束后，实际上没有必要知道存储的值，因此我们就可以带着在一次递归调用中已经用过的那些值goto到函数顶部。按照上述逻辑修改上面的尾递归代码如下：

int fibonacci_Tailrecursive(int n, int res1, int res2)
{
top:
    if(n < 0)
        return 0;
    else if(n == 0)
        return res1;
    else if(n == 1)
        return res2;
    else
    {
    	n = n - 1;
    	int temp = res1;
    	res1 = res2;
    	res2 = temp + res2;
    	goto top;
    }
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18

上面使用goto语句是为了说明编译器是如何自动去除递归的，我们还可以将其修改为迭代循环的形式，修改为循环后的代码如下：

int fibonacci_Tailrecursive(int n, int res1, int res2)
{
    if(n < 0)
        return 0;
        
    while(1)
    {
    	if(n == 0)
        	return res1;
    	else if(n == 1)
        	return res2;
        
        n = n - 1;
    	int temp = res1;
    	res1 = res2;
    	res2 = temp + res2;
    }
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18

从上面尾递归的去除过程可以看出，尾递归的去除还是挺简单的，以致于某些编译器能够自动完成。那是不是所有的递归代码都可以改为这种迭代循环的非递归写法呢？

笼统地讲，是的。因为递归本身就是借助栈来实现的，只不过我们使用的栈是系统或者虚拟机本身提供的，我们没有感知罢了。如果我们自己在内存堆上实现栈，手动模拟入栈、出栈过程，这样任何递归代码都可以改写成看上去不是递归代码的样子。

虽然非递归程序一般确实比等价的递归程序更快，但是速度优势的代价是由于去除递归而使得程序的可读性变差，特别是在现代复杂的软件工程协作中，自己的代码可能会被团队中其他成员频繁阅读。

本章数据结构实现源码下载地址：https://github.com/StreamAI/ADT-and-Algorithm-in-C/tree/master/datastruct

更多文章：

注：本文转载自blog.csdn.net的流云IoT的文章"https://blog.csdn.net/m0_37621078/article/details/103621357"。版权归原作者所有，此博客不拥有其著作权，亦不承担相应法律责任。如有侵权，请联系我们删除。
复制链接
相关推荐
发表评论

评论记录：

未查询到任何数据！