一、什么是数据结构
在介绍什么是数据结构之前,先拿绘画做个类比。一般人画画通常就直接画了,比如要画水里的两条金鱼就直接从某一个部分开始,画到后来比例不对,而且常常画得不像。专业画家不是这么画的,他们会把金鱼分解成几个简单的几何图形,比如头是一个大圆和两个小圆(即两个眼睛),身子是一个椭圆,鳍和尾巴是几个三角形。如果是几条金鱼,他会先把位置安排好,为了画面美观,主要景物的布置可能要符合一些几何图形的形状,这些都用淡淡的铅笔或者淡墨勾好了,才把圆、椭圆和三角形经过平滑过渡,画成金鱼,不掌握这种绘画方法,永远走不进专业的大门。
在绘画和摄影中,这些基本的几何图形使用的远比一般人想象的多得多,特别是在构图上,只不过当最终的作品完成时,你看不太出来最早的构图框架而已。对于计算机科学来讲,写一个能够完成特定功能的程序,就相当于是作一幅画,在理解具体需求之后,抽象出具体的基本几何形状这样的基础块,然后用算法将这些模块进行组合,写出符合需求的程序。这些程序中基本的几何图形,就是计算机的数据结构。如果说一幅画是点的有机组合,几何图形反应出点之间常用具体的关系,那么在计算机科学中,数据就等同于点,数据结构就是数据中常用的具体关系。
计算机科学主要是利用计算机解决我们现实生活中遇到的各种问题或需求的技术,我们要想让计算机能解决现实生活中遇到的问题或需求,首先需要将现实问题抽象为数学模型,转换为对数据的计算和处理,计算机才能够发挥作用。
将现实世界的数据组织成为一些具有特定关系的逻辑结构,再把这些逻辑结构的数据映射到计算机的物理存储结构中,这便是计算机科学中的数据结构要解决的问题。数据按照一定的关系结构映射到计算机内存中后,需要在内存中处理这些数据结构,如何在内存中操作这些数据结构就是算法要解决的问题了。对同一个现实问题,使用不同的数据结构和算法进行存储和计算,表现出来的效率是不一样的,如何评价这些数据组织与存储结构及其对应的操作方法,这便需要引入时间和空间复杂度这把标尺了。
数据结构的组成框架如下图所示:
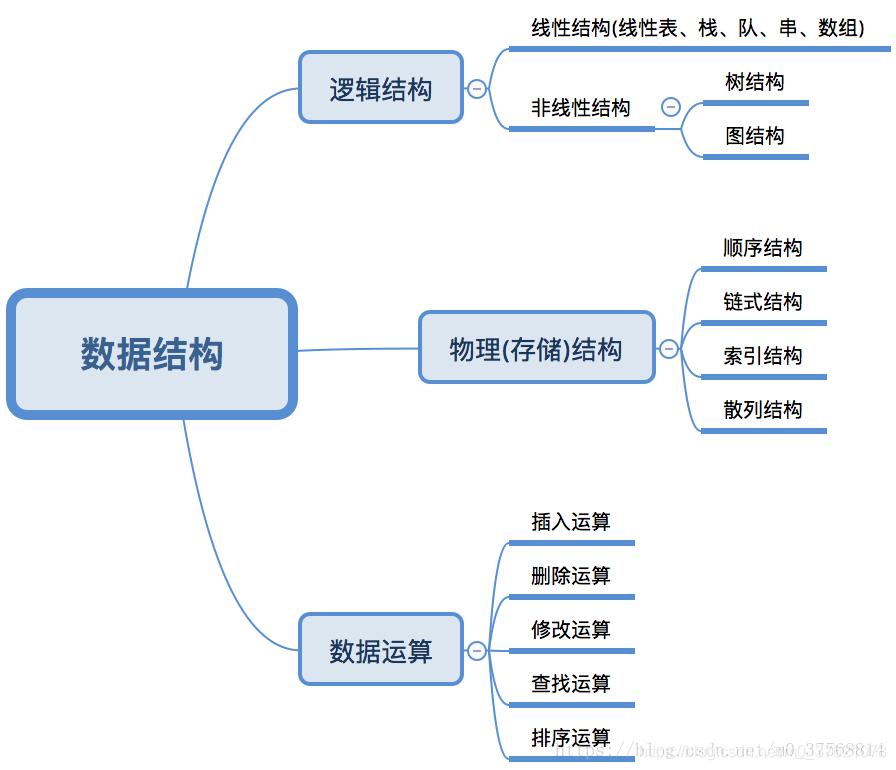
对于不同的数据结构有不同的处理方法(也即算法),所以数据结构和算法是相辅相成的。数据结构是算法操作的对象或载体,算法要作用在特定的数据结构上才能发挥作用。世界著名计算机科学家、因为发明PASCAL而获得图灵奖的N.Wirth教授写过一本书:《数据结构 + 算法 = 程序》,很好的讲清楚了这三者之间的关系。
1.1 数据的物理存储结构
前面介绍了现实世界的数据要想交给计算机去处理,需要以计算机能识别易操作的方式进行。将现实世界的数据组织成具有特定关系的逻辑结构,是为了方便我们理解这些数据之间的逻辑关系,这些数据要想方便计算机处理,还需要映射为方便计算机存储和处理的结构。
计算机在处理数据时,是将数据暂时存储在内存中的,处理器从内存中获取计算局部数据,并将计算结果再存储到内存中。内存的最基本单位叫做存储单元(一般为一个字节),存储单元相当于一个空盒子,可以放置数据,为了便于管理,盒子会给一个编号,这些存储单元的编号就是地址。我们把存储单元的编号或地址都编成0、1、2…这样,这些编号或地址的取值范围就称为地址空间,这个地址空间跟一维坐标轴一样,所以是一维地址空间。
一般一个存储单元可以放置一个单位的数据,假如需要放置多个数据,我们有两种放置方案(物理存储方案):一个挨一个的连续放置数据;不连续的放置数据。一个数据结构的多个数据间包含特定的关系,存储到内存中这个关系当然也需要保留。连续放置的数据天然存在邻接关系,可通过地址偏移量(索引、下标)互相访问;不连续放置的数据就需要赋予其相互关系的属性,比如在一个数据中标记下一个数据的地址或编号(指针),通过这个指向关系,我们可以在不连续的放置方案中依次查找我们所需要的数据。为什么会有不连续的放置方案呢?原因很简单,一个主要原因是,内存的空间利用率高、碎片少、删除旧有的数据很容易。
由于计算机内存是一维线性地址空间,计算机的物理存储结构或方案只有两种:
- 连续存储(也称顺序存储结构):包含数据间的邻接关系,随机访问元素很快,但从中间插入或删除元素较慢,且地址空间大小在创建时指定,后面几乎不可更改,缺乏弹性;
- 不连续存储(也称链式存储结构):包含数据间的指向关系,地址空间大小可根据需要动态调整,从中间插入或删除元素很快,但随机访问元素较慢,且需要额外存储元素间的指向关系。
1.2 数据的逻辑组织结构
了解了不同数据在计算机内存中的物理存储结构,那么如何将现实世界中各式各样的数据放入到物理内存中?我们可以分两步走,第一步是将现实世界中的数据组织成具有特定关系的逻辑结构,第二步再把逻辑结构的数据映射到物理结构中。
数据的逻辑结构是从现实世界抽象出来的,可以直观反映数据之间的逻辑关系。比如,线性表这种最基本的抽象数据结构,最早起源于商业上的办公自动化,在商业上,报表是一种最常见的数据组织形式,而在管理上最多见的则是人员或者物资的记录等,它们被抽象为线性的数据,然后按照1、2、3…的顺序排列出来便于后期检索查阅。为此,很有必要设计一种抽象的数据结构概括所有这些顺序排列和存储的数据,它就是线性表。当然,随着计算机数据规模的扩张,未必能给所有数据都赋予一个编号、结构化的存储,但是它们依然遵循一个顺序的特征,比如电商交易的日志记录按照所发生的时间顺序一条条线性的记录,因此线性表的性质它们都有。
线性表本身是一个抽象的逻辑结构,映射到物理存储结构中,可以使用顺序存储结构实现,也可以使用链式存储结构实现。 使用顺序存储结构实现的线性表最常见的就是数组,数组这种邻接关系保证了数据的查询很快,从中间增加删除很慢(需要移动后面的数据占据或腾出空间),且容易因为连续存储地址空间不足导致扩展比较麻烦。链表这种指向关系正好可以跟数组形成互补,从中间增加删除很简单(只需要改变前后数据的指向关系),不需要连续存储地址空间比较方便扩展,但数据的查询比较慢(只能依据数据指向关系从链表头逐个遍历查询)。
数据的逻辑结构主要有两个属性:一个属性是数据的值,另一个属性是数据之间的关系。数据之间的逻辑关系除了上面介绍的线性关系,还有更复杂的树状关系、网状关系(图)、归属关系(集合)等,这些逻辑关系映射到物理存储结构中,既可以通过顺序存储结构实现,也可以通过链式存储结构实现,根据现实需求与两种物理存储结构的优缺点选择采用哪种物理存储方案实现。
二、线性表
前面已经介绍了线性表这种最基本数据结构的起源,将现实世界的数据抽象为前接后继的线性逻辑关系。同时介绍了线性表使用顺序存储结构与链式存储结构的优缺点,下面分别介绍这两种物理存储结构是如何实现线性表的。
2.1 顺序存储结构实现:顺序表
数组我们已经很熟悉了,我们创建一个数组类型,只需要声明数组元素的类型和数目就可以了。因为数组元素间是连续存储的邻接关系,我们只需要知道该数组在内存中存储的首地址和该数组中某元素的下标(实际上是地址偏移量),便可以知道该数组中某元素的物理存储地址,便可以顺利访问该数组元素了。数组元素间的线性关系如下:
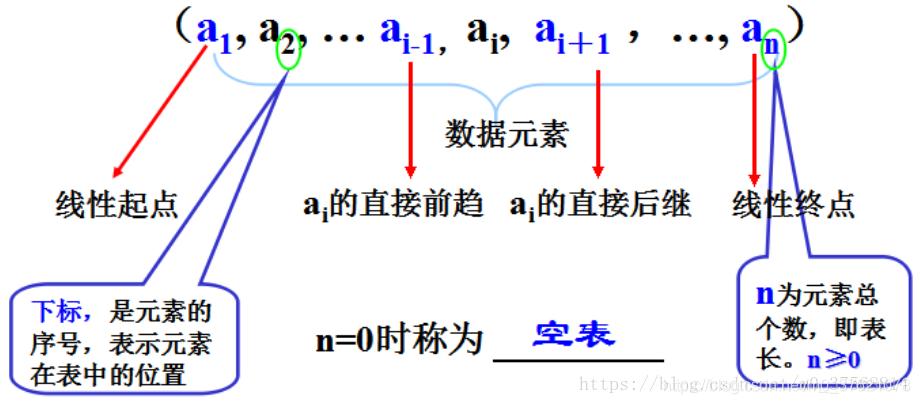
我们初始化一个数组,数组名a就保存了该数组在内存中存储的起始地址(线性起点),后面跟数组元素下标(比如a[0]),就可以访问该元素。数组元素下标为何从0开始呢?既然把下标作为数组元素相对首地址的偏移量,首元素存储地址相比该数组起始地址的偏移量为0,数组首地址加数组某元素相对首元素的地址偏移量(由下标乘以该元素类型占用字节数获得)可以直接得到该数组元素的物理存储地址(a[k]_address = base_address + k * type_size)。数组元素的操作方法示例如下:
// datastruct\array_demo.c
int main(void)
{
// Create a one-dimensional array
int a[6] = {1, 3, 4, 5};
printf("a = %X, *a = %d\n", a, *a);
printf("a[0] = %d, a[1] = %d\n", a[0], a[1]);
// Modifying array element values
a[1] = 7;
// Accessing array element values
for(int i = 0; i < 6; i++)
printf("a[%d] = %d\n", i, a[i]);
printf("\n");
return 0;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
上面数组操作示例程序运行结果如下:
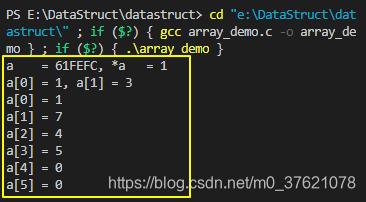
对某种数据结构的操作方法主要有五种:增、删、改、查、排序,根据需要还可以提供初始化构造函数与释放析构函数。对于数组我们最常使用的操作方法是修改和随机访问(见上面的示例代码),前面介绍排序算法时,也是以数组方式存储数据的,所以数组的排序操作也比较方便。因为数组从中间新增或删除元素效率较低,所以这两种操作方法不常用(如果想用也可以自己实现),这里就不展示了。
- 多维数组
我们经常使用的Excel是以二维表格的形式管理的,常用的字符串数组也是以二维数组的形式管理的(一个字符串是以一维字符数组的形式保存的),我们学过的矩阵也是以二维甚至多维的形式表示的。
多维数组的物理存储结构依然是连续的,也即多维数组中的所有元素在物理内存中都是线性连续排列的。多维数组只是一种逻辑组织结构,相当于把一个一维数组分割成几段分别管理。比如二维数组就是把一维数组分割成多段,每一段称作一行,每行相同序号的元素共同构成一列,图示如下:
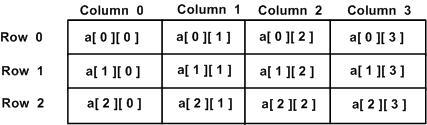
多维数组这种逻辑组织结构是为了方便我们更最直观理解数据,实际在内存中是以一维线性连续方式存储的(在内存中不体现维度)。多维数组的操作跟一维数组类似,下面给出一个参考示例程序:
// datastruct\array_demo.c
#include - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
上面二维数组的示例程序执行结果如下:
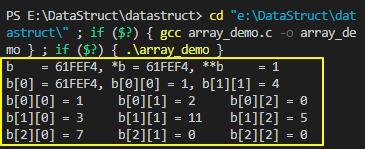
数组算是最常用的一种数据结构了,依序存取、随机访问都比较快速方便,但想要在中间插入或删除元素就会比较麻烦,为了保证元素间的邻接关系,元素之间不能存在空位,因此要从中间插入或删除一个元素,后面的所有元素都要向后或向前挪动位置,以腾出空间或占据空位,这就很影响效率了。对于需要经常在中间插入或删除数据的场景怎么办呢?这就需要采用链式存储结构来实现线性表了。
2.2 链式存储结构实现:链式表
采用链式存储结构实现线性表,每个元素就需要显式存储数据之间的指向关系了(顺序存储结构具有隐式的邻接关系)。线性表中数据之间的关系是线性关系,也即前接后继的关系,要能从头部数据沿着某个方向逐个遍历到线性表中的所有数据。元素间的线性关系要求前一个元素能找到后一个元素,最简单的就是保存后一个元素的物理存储地址,指针变量正好存储的是地址值,很适合拿来保存下一个数据的存储地址,也即指针可以显式保存线性表中数据之间的指向关系。
按照上面的分析,链表中的元素至少包含两个变量:一个用来存放数据的值;另一个用来存放指向下一个元素地址的指针。如果把链表中的某个元素称为结点(Node),每个结点包含数据域与指针域两部分,数据域用来存放该结点的数据信息,指针域用来存放该结点与其它结点的指向关系信息,这两部分需要封装为一个整体共同保存该结点的全部信息。什么数据类型具有封装功能呢?C语言的结构体和C++的类都具有封装功能,对于面向过程的C语言来说,自然使用结构体来封装链表结点的全部信息,封装示例如下:
struct Element
{
DataType data; //DataType根据实际元素类型决定
struct Element *next; //next存储下一个元素的地址
}
struct Element a = {data,NULL};
struct Element *List = &a; //这个List就是一个“链表”
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
为了便于访问一个链表中的任一元素,常需要在链表头部放置一个头结点(链表头),作为该链表的名称(一般称head,类似于数组名)。链表头可以作为第一个结点(第一个数据域保存用户数据的结点)使用,也可以在链表头数据域存放该链表的一些特征信息(比如元素个数),该链表头的指针域则指向第一个结点,后者更为常用。链表元素间的逻辑结构如下图所示:

链表头独立于其余元素,保存整个链表的统计信息能带来不少好处。首先链表头数据域保存链表元素个数,当我们查询链表中元素数目时,就不必遍历一遍,可以直接返回,特别是对元素数目很大的情况下更是如此。
链表头的数据域保存指向第一个结点的指针,可以方便往链表首部也即第一个结点前插入结点(独立的链表头永远在最前面);如果需要经常往链表末尾插入结点,每次遍历到链表末尾结点再操作其指针域就比较耗时了,可以在链表头指针域内再新增一个指向最后一个结点地址的指针变量,这样从链表首尾插入新的结点都比较快了。
带独立链表头的链表结点数据结构如下(把指针域放前面为了便于强制类型转换):
//Node是普通结点,pNode是指向普通结点的指针
struct Node {
struct Node *next; //指向下一个元素的地址
ElementType Element; //可以是数据集合或其它的数据结构
};
typedef struct Node *pNode;
//HeadNode特用于头结点,List也只能指向头结点
struct HeadNode {
struct Node *next; //指向第一个结点的地址
int size; //保存链表中有效元素数目
};
typedef struct HeadNode *List;
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
了解了链表的数据结构描述,接下来看链表支持的操作方法。前面说了,链表的插入、删除操作比较方便,链表的查找、访问相比数组低效些。由于链表不支持随机访问,因此不适合进行排序操作,所以链表主要的操作就是创建、插入、查找、删除这三种。
- 链表创建
链表创建实际上就是创建链表头结点,主要分为两步,先为头结点分配内存空间,再初始化头结点的各成员变量,最后返回链表头结点指针。参考实现代码如下:
// datastruct\slist.c
List Create(void)
{
List ptr = malloc(sizeof(struct HeadNode));
if(ptr == NULL)
printf("Out of space!");
ptr->size = 0;
ptr->next = NULL;
return ptr;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 链表元素查找
链表不支持随机访问,查找操作一般采取从头遍历的方法进行。对于链表来说,并没有下标或编号,一般的查找操作是查询某元素值在该链表中的位置,如果找到则返回该节点的指针,若找不到则返回空指针。参考实现代码如下:
// datastruct\slist.c
pNode Find(List L, ElementType x)
{
pNode ptr = L->next;
while (ptr != NULL && ptr->Element != x)
ptr = ptr->next;
return ptr;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 链表结点插入
链表结点的插入相对复杂些,涉及到元素关系的调整,也即指针指向的变化。先看下图示:
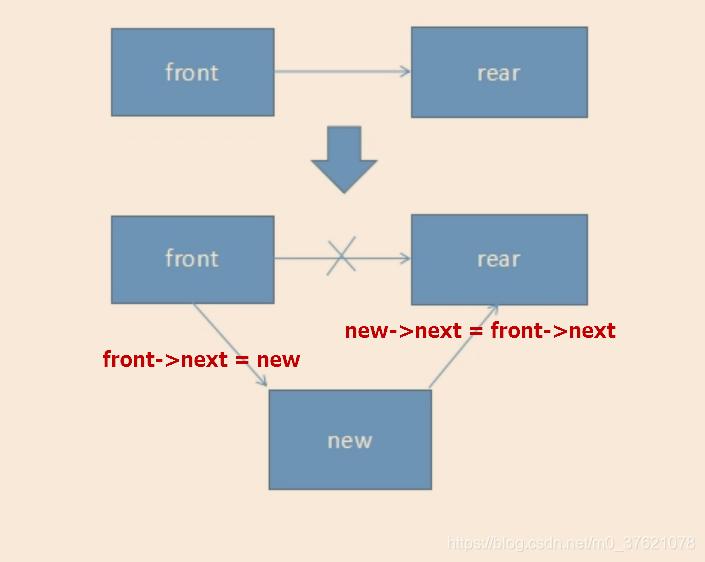
理清了链表结点插入过程中,元素关系的变化,就方便实现插入操作函数了。我们一般在某一个结点后面插入一个元素,元素插入过程也可以分为两步,创建一个新结点并为其数据域赋值,调整新结点与插入点的元素指向关系。参考实现代码如下(注意考虑在链表头后插入与尾结点后插入的情况):
// datastruct\slist.c
void Insert(List L, pNode Position, ElementType x)
{
pNode pTemp = malloc(sizeof(struct Node));
if(pTemp == NULL)
printf("Out of space!");
pTemp->Element = x;
if(Position != NULL)
{
pTemp->next = Position->next;
Position->next = pTemp;
L->size++;
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 链表结点删除
链表结点的删除操作跟插入操作类似,同样需要调整删除点前后元素间的指向关系,图示如下:
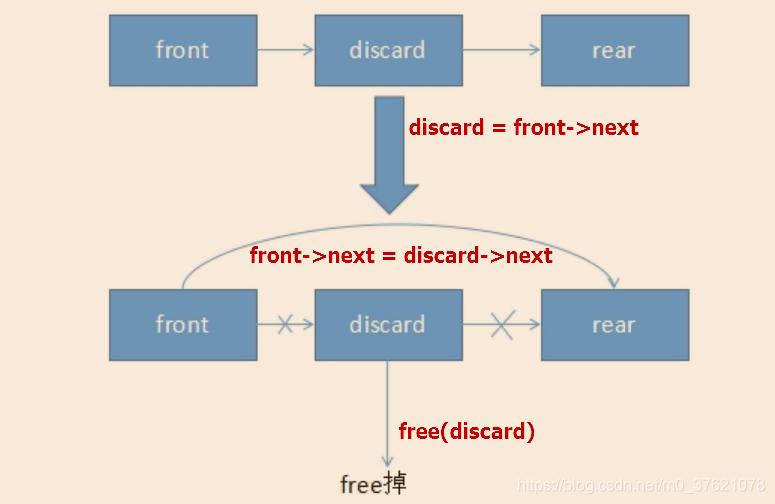
理清了链表结点删除过程中,元素关系的变化,就方便实现删除操作函数了。链表删除操作一般是删除链表中等于某个值的元素,也可以分为两步,首先根据元素值找到其在链表中的前驱结点(因单向链表无法获得其前一个元素的地址),再删除其前驱结点后面的一个结点(即等于要删除目标元素值的结点)即可。参考实现代码如下(注意考虑删除首结点与尾结点的情况):
// datastruct\slist.c
void Delete(List L, ElementType x)
{
pNode Prev = (pNode) L;
while (Prev->next != NULL && Prev->next->Element != x)
Prev = Prev->next;
if(Prev->next != NULL)
{
pNode pTemp = Prev->next;
Prev->next = pTemp->next;
free(pTemp);
L->size--;
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
单向链表的常用操作就介绍完了,总结链表操作过程中元素间指向关系变化图示如下:
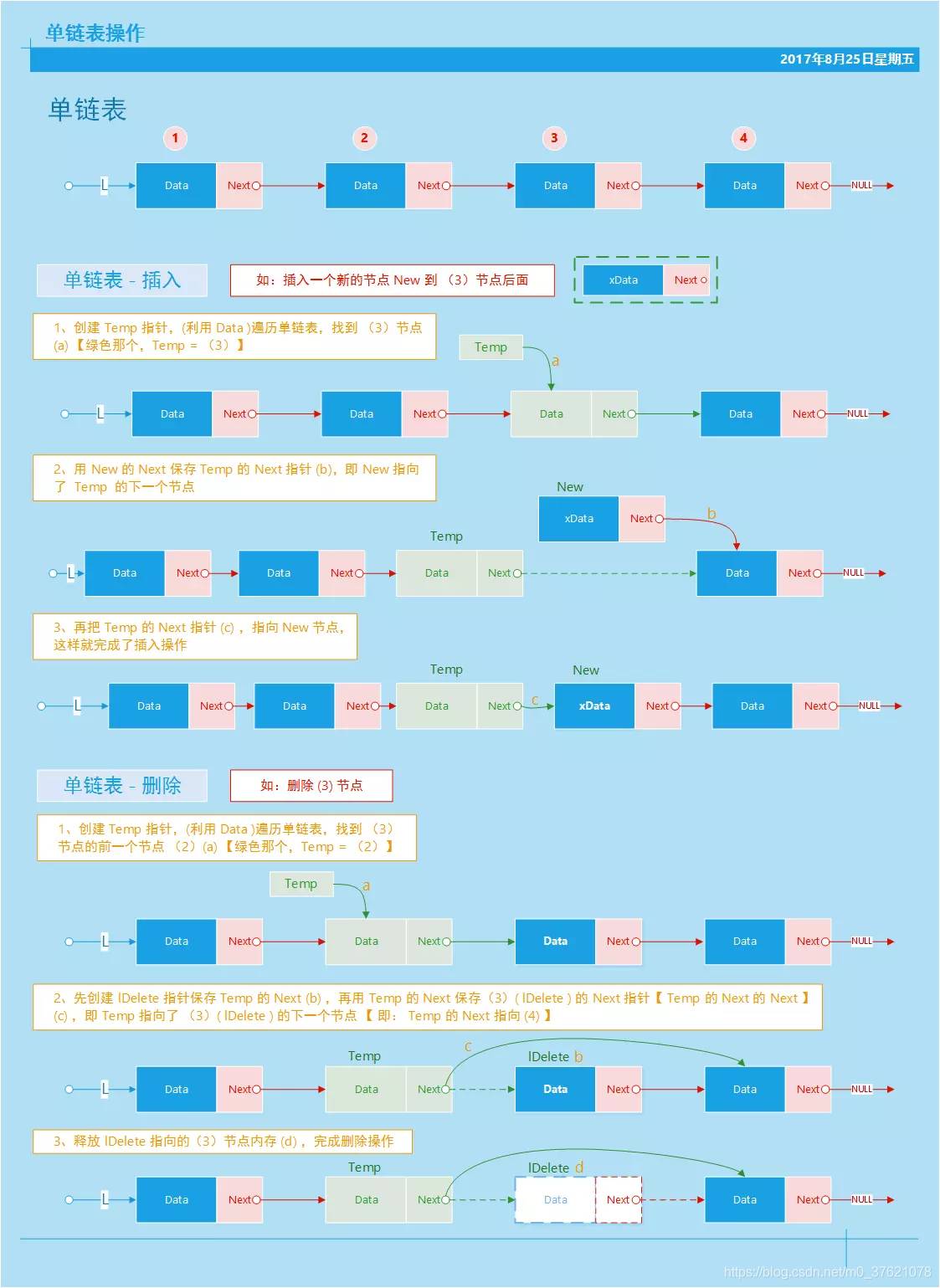
下面给出一个链表操作的示例程序:
// datastruct\slist.c
#include - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
上面单向链表操作示例程序的执行结果如下:
2.2.1 双向链表
前面介绍的是单向链表,特点是只能单向从前往后遍历查找下一个元素的地址。单向链表往靠近链表头的位置插入或删除结点比较高效,假如需要经常往链表尾部插入或删除结点,每次都遍历一遍就比较低效了,特别当元素数目比较多的情况下。虽然前面也介绍了一种方法,在链表头指针域增加一个指向末尾结点地址的指针,可以解决经常插入删除末尾结点的情况,但其余靠近末尾的结点(比如倒数第二个结点),这种方案就无能为力了。
既然链表头指针域可以分别包含指向首结点与尾结点地址的指针,很容易想到,在普通结点的指针域也可以增加一个指向其前一个结点地址的指针,这就可以实现双向遍历了,这种支持双向遍历的链表叫做双向链表。双向链表的元素间逻辑结构图示如下:

按照上面的图示,给出双向链表结点的数据结构表示(把next指针放前面同样为了方便链表头与普通结点的强制类型转换):
//Node是普通结点,pNode是指向普通结点的指针
struct Node {
struct Node *next; //指向下一个元素的地址
ElementType Element; //可以是数据集合或其它的数据结构
struct Node *prev; //指向前一个元素的地址
};
typedef struct Node *pNode;
//HeadNode特用于头结点,List也只能指向头结点
struct HeadNode {
struct Node *next; //指向第一个结点的地址
int size; //保存链表中有效元素数目
};
typedef struct HeadNode *List;
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
双向链表的创建与查找过程跟单向链表类似,这里就略去了,重点说下双向链表的插入与删除操作。先看双向链表的插入过程:
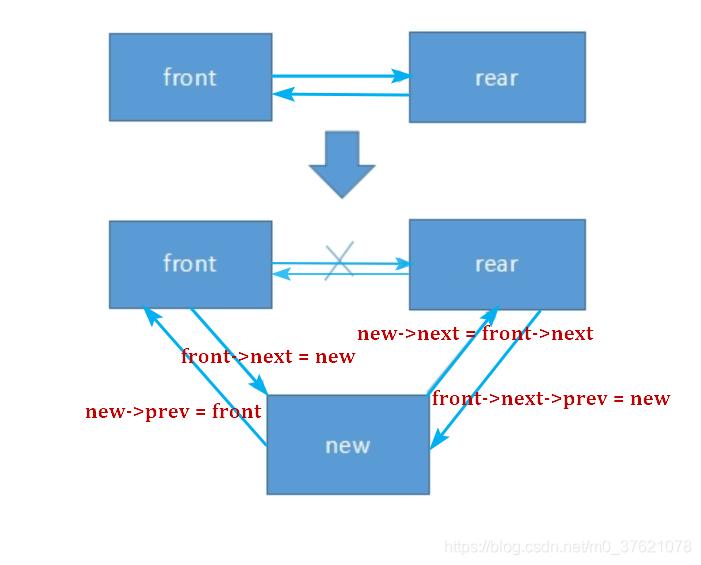
双向链表结点插入过程同样需要考虑在链表头后插入和尾结点后插入的情况,由于涉及到访问下一结点的前驱结点,假如下一结点不存在,按照上面的图示编程就会出错,所以需要按下一结点是否存在两种情况编写代码,参考实现代码如下:
// datastruct\dlist.c
void Insert(List L, pNode Position, ElementType x)
{
pNode pTemp = malloc(sizeof(struct Node));
if(pTemp == NULL)
printf("Out of space!");
pTemp->Element = x;
if(Position != NULL)
{
if(Position->next == NULL)
{
Position->next = pTemp;
pTemp->next = NULL;
pTemp->prev = Position;
} else {
Position->next->prev = pTemp;
pTemp->next = Position->next;
Position->next = pTemp;
pTemp->prev = Position;
}
L->size++;
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
双向链表的删除图示如下:
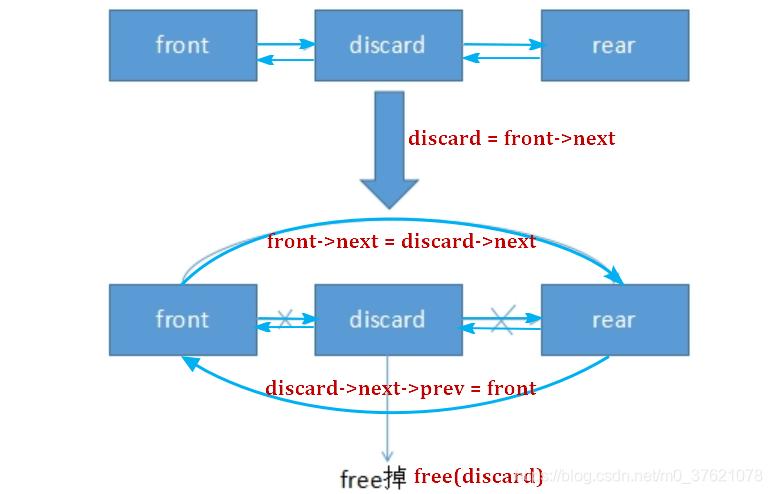
双向链表结点删除过程同样需要考虑删除首结点与尾结点的情况,与上面的插入过程类似,也需要按下一结点是否存在两种情况编写代码,参考实现代码如下:
// datastruct\dlist.c
void Delete(List L, ElementType x)
{
pNode pTemp = Find(L, x);
if(pTemp != NULL)
{
if(pTemp->next == NULL)
{
pTemp->prev->next = NULL;
} else {
pTemp->next->prev = pTemp->prev;
pTemp->prev->next = pTemp->next;
}
free(pTemp);
L->size--;
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
类比单向链表,给出双向链表操作过程中元素间指向关系变化图示:
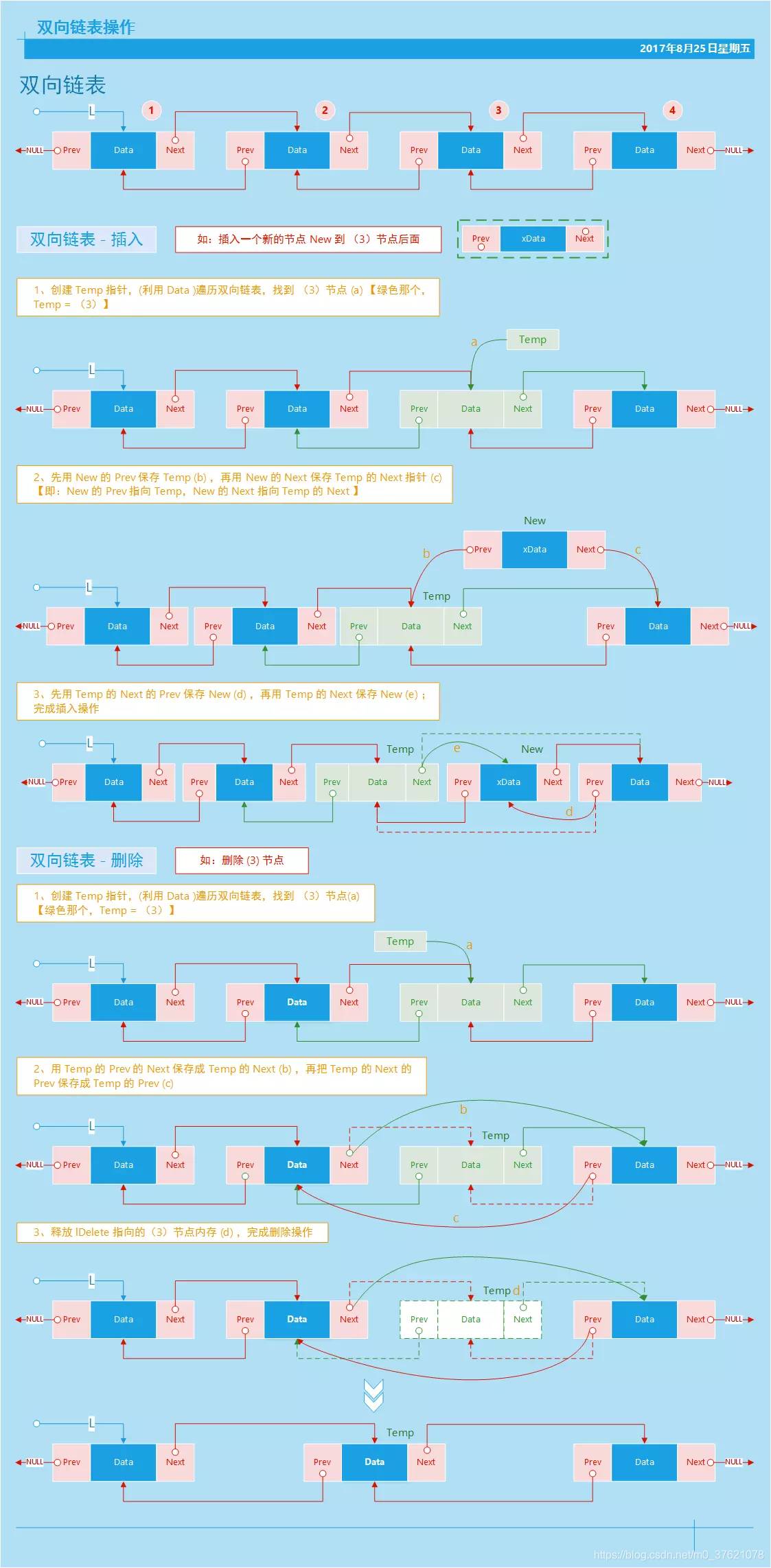
下面给出一个双向链表操作的示例程序:
// datastruct\dlist.c
#include - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
上面双向链表操作示例程序的执行结果如下:

2.2.2 循环链表
不管是单向链表还是双向链表,从链表头开始访问,都可以访问到最后一个结点,也即尾结点的指针域中指向下一个结点地址的指针为空(NULL)。如果我们让尾结点指针域中指向下一个结点地址的指针指向首结点,链表元素就构成一个环形,可以循环遍历,这种链表被称为循环链表(分为单向循环链表与双向循环链表)。循环链表中元素间的逻辑组织结构如下:
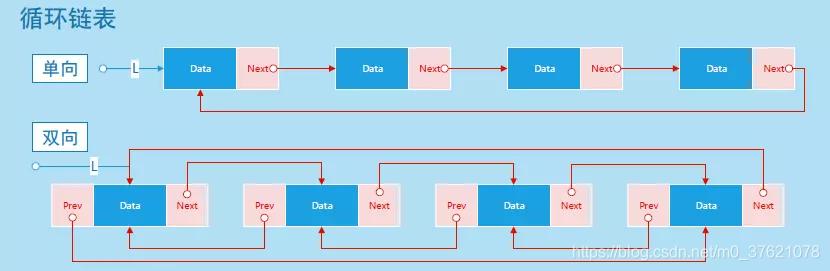
循环链表的操作跟单向或双向普通链表类似,需要注意首结点与尾结点指针域的处理,同时也需要注意查找的结束条件。比如查找某元素结点时,就不能把指向下一个结点的指针为空作为查询结束条件了,可以按链表头中保存的元素个数(L->size)查找,当遍历L->size个元素后便可作为查找结束条件。也可以先保存查找遍历的初始元素地址,当遍历到初始元素时(下一个结点的地址与初始元素地址相同),便可作为查找结束条件。
由于循环链表没有前两种常用,这里就不再给出其操作方法的实现代码了,读者感兴趣可以自己实现,可参考循环链表操作过程中元素间指向关系变化图示:
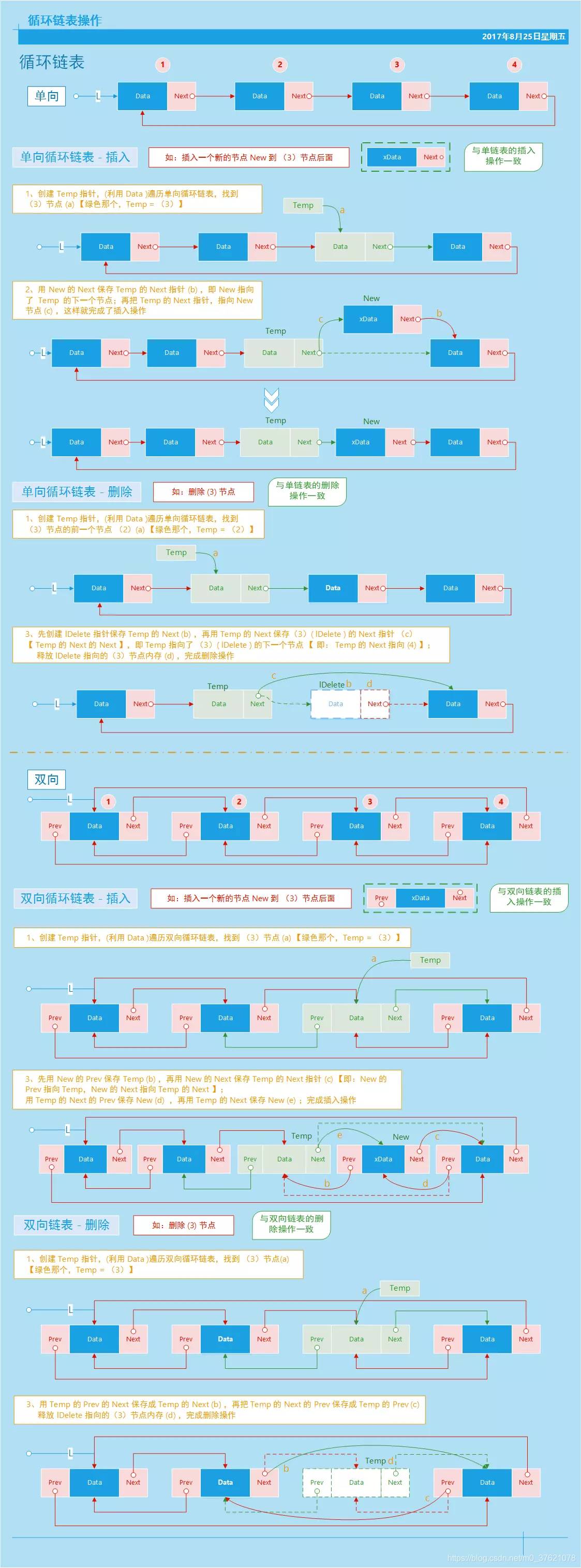
2.2.3 组合链表(广义表)
线性表的链式存储结构最基本的就是上面介绍的单向链表、双向链表、循环链表,这些链表在操作系统的资源管理中很常见,比如新创建或初始化一个线程,该线程对象就可以插入到线程链表中由系统协调管理。
- 跳跃链表
由于链表的查询效率较低,假如链表中元素数目很多,每次查询都需要遍历链表就很耗费时间了。特别是对实时性要求较高的场景,比如操作系统定时器管理,每创建一个定时器资源,都可以根据其超时触发时间插入到定时器管理链表中,但每次查找插入点与删除点很耗费时间,影响操作系统与定时器对象响应的实时性。
前面介绍了二分查找,对于已排序的数据序列,采用二分查找(时间复杂度O(logN))比线性查找(时间复杂度O(N))效率提升了很多,我们是否可以借鉴二分查找的思想呢?
在链表中插入新元素结点时,我们可以仿照插入排序,使新结点插入后,链表元素依然是有序的,操作系统定时器资源链表便是这么管理的。对于有序链表的查找,怎么实现二分操作呢?
最简单的方法是从原链表中每两个结点提取一个结点到上一层,可以把抽出来的那一层叫作索引层。接下来,在上面第一级索引的基础之上,每两个结点再抽出一个结点到第二级索引。依此类推,直到最上层索引只有两个结点为止,就为原链表创建好了完全的索引层,可以借助这些索引层实现二分查找O(logN)的效率。下面给出一个索引层图示:
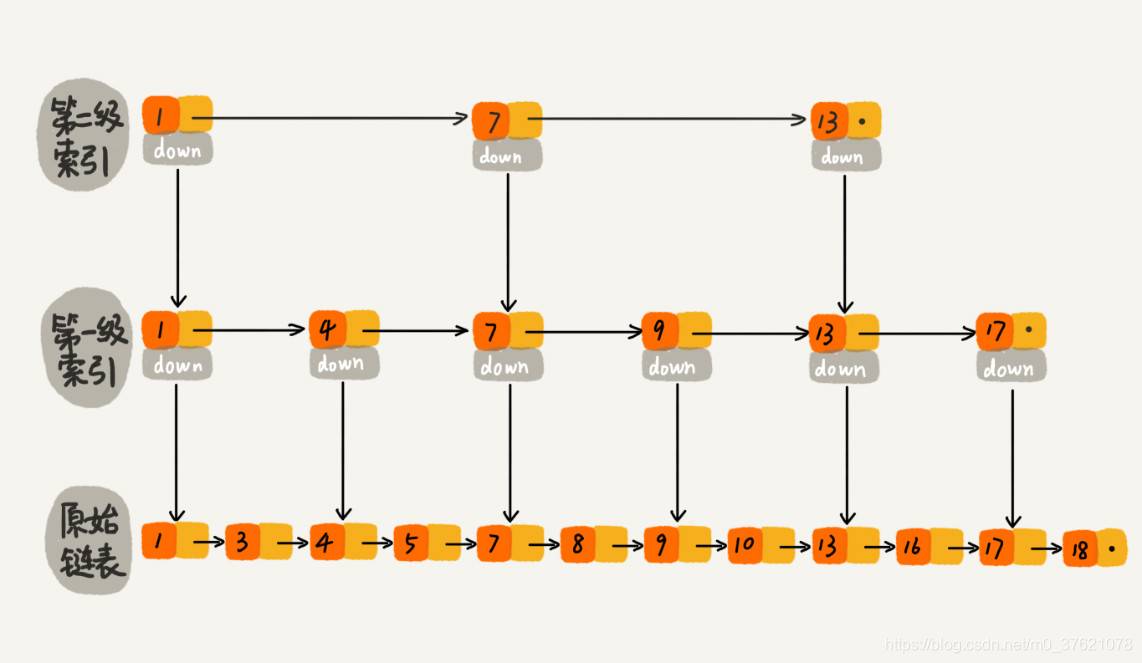
这种链表加多级索引的结构,就是跳越链表(简称跳表)。原链表与多级索引层的部分结点之间也组织成一个个线性表,通过这些线性表就可以从上到下随索引层级减小跳跃跨度,直到跳跃到原链表找到目标元素或找不到目标元素而返回。跳跃链表的工作过程如下所示:

定义跳跃链表时,根据需要选择链表层级(也即链表个数),如果链表层级过多会增加编写代码的复杂性,切会增加占用内存空间。下面给出一个跳跃链表数据结构的定义示例:
//HeadNode特用于头结点,List也只能指向头结点
struct HeadNode {
struct Node *next; //指向当前索引层链表首结点的地址
struct HeadNode *down; //指向下一索引层链表头的地址
int size; //保存当前索引层链表中有效元素数量
int level; //保存当前索引所在层级
};
typedef struct HeadNode *ListHead
ListHead SkipList[MAX_LEVEL]; //SkipList以数组形式保存每层链表头指针,首地址为第一层原链表头指针
//Node是普通结点,pNode是指向普通结点的指针
struct Node {
struct Node *next; //指向当前索引层链表后一个结点的地址
struct Node *down; //指向下一索引层链表对应结点的地址
ElementType Element; //可以是数据集合或其它的数据结构
};
typedef struct Node *pNode;
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 多重链表
线性表顺序存储结构中的数组存在多维数组,链式存储结构中的链表自然也存在多重链表。多重链表相比多维数组自然也有插入删除元素结点方便,不要求存储空间的连续性,节省内存空间且扩展方便等优点。
我们举例假设要存储一所大学的学生选课情况,然后允许用户执行两个操作,一个是查询某名学生选了哪些课程,另一个是查询某个课程有哪些学生选择了。假设学生人数大约为5000人,学校所有开设的课程大约有1000门,一个学生选的课程不超过10门。如果我们使用二维数组来存储学生选课的信息,总共将需要500万个元素,而平均来说其中只有5万个元素是“打勾”的(某学生选择了某门课程),其它495万个元素都是“空”的,这样的浪费显然是巨大的。
二维数组存储学生选课信息为何会有这么大的浪费呢?因为数组连续存储的特性,要求其要能容纳最大维度,且中间不能有空位。链表相比数组的一个优势就是其存储可以是不连续的,允许中间有空位,对于这么中间有大量空位的多维数据,链表就能发挥出其节省内存空间的优势。我们使用二重链表存储学生选课信息,元素结点间的逻辑组织结构如下图示(相只需要5万个结点,相比二维数组节省了90%的内存空间):
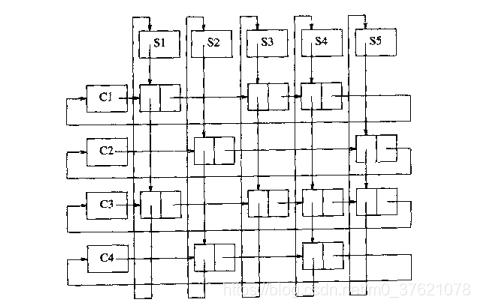
对于多维数组来说,因为所有元素在物理内存中还是线性邻接的,所以依然不需要显式存储元素间的逻辑关系,靠下标依然可以访问所有元素。
对于多重链表来说,每增加一个维度就需要在指针域中增加新的元素结点指向关系,比如上面存储学生选课信息的二重链表,结点元素的数据结构可以定义为如下形式:
struct Node
{
bool choose;
struct Node *hNextNode;
struct Node *vNextNode;
struct Student *student;
struct Course *course;
}
struct Student
{
char name[SIZE];
struct Node *firstNode;
}
struct Course
{
char name[SIZE];
struct Node *firstNode;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
2.3 链表的游标实现:游标数组
前面介绍的链式表的实现依赖于指针变量,但有些编程语言(比如BASIC、FORTRAN等)不支持指针,如果需要链表而又不能使用指针,那么就必须使用另外的实现方式了。
回顾数组怎么获知元素地址的,数组元素地址 = 数组存储首地址 + (数组下标或元素序号 X 单个元素占用字节数),也即我们可以通过数组元素下标来获得该元素地址,所以我们可以使用数组来模拟链表的实现。
由于链表中的元素不再是邻接关系,用数组模拟链表就要显式存储元素间的指向关系了,元素地址使用数组下标表示,由于指向下一个元素的下标并不固定,我们称这种指向下一个元素的下标为游标,这种用数组实现的链表称为游标数组,也称为静态链表。
游标数组(或静态链表)既然在内存中是以顺序表的形式管理的,自然继承了数组的优缺点,访问高效,不能动态变化大小。但由于使用了游标,挣脱了数组元素间邻接关系的限制,又具有一些链表的优点,插入、删除元素比较高效。为了方便插入新元素,初始分配给游标数组的空间一般要大于需求,也即保留一定的预留空间,让游标数组在一定程度上实现变长数组的效果。
游标数组既然要显式存储元素间的指向关系,也需要一个结构体封装元素的数据域与指针域,封装示例如下:
//Node是普通结点,pNode是指向普通结点的指针
struct Node {
ElementType Element; //元素数据类型
int next; //指向下一个数组元素的下标
};
struct Node CursorSpace[SpaceSize]; //为游标数组分配的线性连续地址空间
- 1
- 2
- 3
- 4
- 5
- 6
- 7
从上面的数据结构也可以看出,游标数组的内存空间是提前创建的,链表中的元素结点则是使用时即时分配、不用时即时释放的,在游标数组中创建、删除元素并不真的涉及到内存的分配与释放,这就需要我们通过代码来分别管理已分配存储单元与未分配存储单元了。
已分配存储单元通过游标的指向关系可以形成一个链表,我们通过头结点即可访问全部已分配存储单元;未分配存储单元和已释放存储单元我们也需要维护一个空闲存储单元链表freelist来管理,否则我们将不知道还有哪些存储单元处于空闲可用状态(虽然可以通过每次遍历获得,但效率太低且不便管理)。
在游标数组初始化后,里面全部都是未分配存储单元(空位置),第一个元素CursorSpace[0]就可以作为freelist的链表头,用来管理这些空位置。既然freelist是一个链表,遍历链表时就有终点,单向链表的某结点指针指向NULL,即表示该结点就是尾结点,NULL指针等价于0的值,所以我们可以让freelist的最后一个结点的游标设置为0,表示该链表到为末尾了。游标0恰是freelist链表头结点的下标,看起来有点像单向循环链表,回顾下单向循环链表的图示(尾结点指针指向首结点地址,而非链表头地址),这里的freelist并非单向循环链表。按照上述逻辑,编写游标数组的初始化函数实现代码如下:
// datastruct\cursor.c
void Init(void)
{
for (int i = 0; i < SpaceSize - 1; ++i)
CursorSpace[i].next = i + 1;
CursorSpace[SpaceSize - 1].next = 0;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
当我们需要空位置时,直接从freelist取首结点(单向链表操作首结点效率最高)也即下标为CursorSpace[0].next的存储单元返回即可,这有点类似于单向链表中的首结点删除,游标数组分配空位置实际上是从freelist链表中移除首结点并返回其游标的过程。当我们删除元素结点时,实际上是将空位置插入到freelist链表首结点中的过程。按照上述逻辑,实现游标数组分配、回收空位置的函数代码如下:
// datastruct\cursor.c
int CursorAlloc(void)
{
int pos = CursorSpace[0].next;
CursorSpace[0].next = CursorSpace[pos].next;
return pos;
}
void CursorFree(int pos)
{
CursorSpace[pos].next = CursorSpace[0].next;
CursorSpace[0].next = pos;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
模拟出了链表操作中内存空间的分配与释放过程,游标数组其余的操作方法实现就跟单向链表类似了,这里就不一一图示详细介绍了,给出游标数组创建、查找、插入、删除操作函数实现代码如下:
// datastruct\cursor.c
typedef int List; //为游标数组模拟的链表头游标定义一个类型别名
List Create(void)
{
List pos = CursorAlloc();
if(pos == 0)
printf("Out of space!");
CursorSpace[pos].Element = 0;
CursorSpace[pos].next = 0;
return pos;
}
int Find(List L, ElementType x)
{
int pos = CursorSpace[L].next;
while (pos != 0 && CursorSpace[pos].Element != x)
pos = CursorSpace[pos].next;
return pos;
}
void Insert(List L, int Position, ElementType x)
{
int pos = CursorAlloc();
if(pos == 0)
printf("Out of space!");
CursorSpace[pos].Element = x;
if(Position != 0)
{
CursorSpace[pos].next = CursorSpace[Position].next;
CursorSpace[Position].next = pos;
CursorSpace[L].Element++;
}
}
void Delete(List L, ElementType x)
{
int prev = L;
while (CursorSpace[prev].next != 0 && CursorSpace[CursorSpace[prev].next].Element != x)
prev = CursorSpace[prev].next;
if(CursorSpace[prev].next != 0)
{
int pos = CursorSpace[prev].next;
CursorSpace[prev].next = CursorSpace[pos].next;
CursorFree(pos);
CursorSpace[L].Element--;
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
将单向链表中的示例程序稍加改写,变成游标数组的示例程序如下:
// datastruct\cursor.c
#include - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
上述游标数组示例程序的执行结果如下:
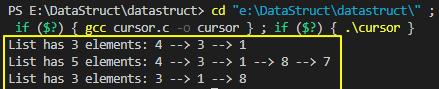
如果要想实现双向游标数组,按照双向链表的操作方法实现代码改写即可。
初始为游标数组分配的空间并不限制静态链表的数量,只要内存空间够用,调用多次Create()方法就可以在同一段内存地址空间中创建多个静态链表(或游标数组),相当于我们链表使用的内存空间限制为我们为游标数组静态分配的空间大小。
游标数组在插入和删除结点时,由于并不需要真的在内存中分配、释放存储资源,而是维护了一个空闲链表freelist管理未使用存储单元,结点的创建与删除比链表更高效。
在操作系统中,内存池与线程池的管理就采用了类似游标数组的结构来管理内存块和线程控制块资源,这也正是看中了游标数组插入、删除结点更高效的优势。对于游标数组可用内存地址空间受限于最初静态分配的地址空间大小,可扩展性有限的缺点,操作系统管理特定资源时是可以接受的,因为操作系统为每类资源分配的空间是有限且可预期、可配置的。
空闲链表freelist对未使用存储单元的管理很有意思,从freelist删除的存储单元是刚刚由free函数放在那里的存储单元。因此,最后被放在freelist的存储单元是被最先取走的存储单元。具有这种特性的线性表在计算机中很常见,因此专门为其量身定制了一个数据结构:栈,它是一种特殊的线性表,下一篇会对其详细介绍。
三、线性表应用示例
3.1 单向链表反转
单向链表反转经常出现在面试题中,这里也简单介绍下,要把链表反向,最简单的是借助可随机访问的数组,将链表中元素依次移到数组中,然后反序取出再插入即可,这种方法需要额外占用存储空间,就不展示了。
单向链表的优势是在首结点前插入移除元素比较高效,假如我们每次取出一个链表的首结点,再依次插入到另一个链表的首结点处会怎样呢?发现经过所插入的新链表正好是原链表的反向顺序,我们就可以用这个逻辑实现单向链表反转的效果了。
实际上,我们不需要维护两个链表,使用一个链表结点指针P指向原链表的首结点,使用另一个链表结点指针T指向P的下一个结点(如果原链表只有一个结点P,不需要反转),将T重新插入链表首部(也即链表头L的后面),指针P->next不断往后移(链接结点P后面的结点越来越少),直到移动到链表尾部,链表就完成了反转,该过程图示如下:
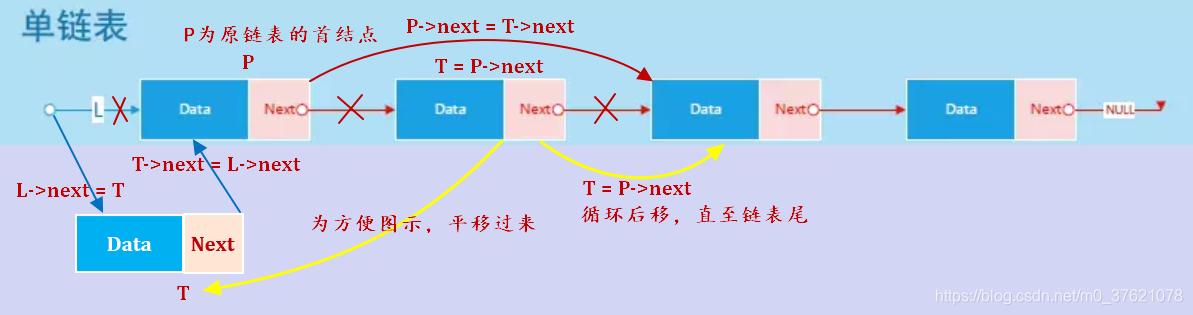
按照上述逻辑,编写单向链表反转的实现代码如下:
// datastruct\slist.c
#include - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
上面单向链表反转示例程序的运行结果如下:
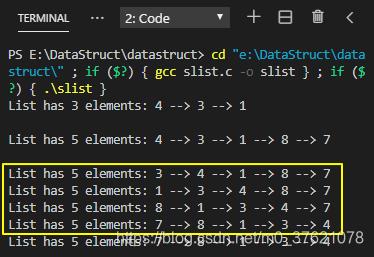
3.2 单向链表排序
如果要对单向链表进行排序,什么排序算法比较合适呢?对于支持随机访问的数组来说,快速排序比较高效,如果数据规模不大插入排序也足够使用。对于不支持随机访问,但插入、移除元素比较高效的链表来说,很容易想到插入排序。
对链表进行插入排序,由于不需要元素搬移,在插入元素过程中可能比数组更高效,对于单向链表来说,由于不支持逆向遍历,只能从前往后寻找插入位置,这点跟使用数组进行插入排序略有不同。
从上面单向链表反转的示例中,我们借用一个链表结点指针P,每次取P->next指向的元素T插入到链表头后面(L->next),直到P后面没有结点便完成了链表反转。假如我们取出的元素T不是插入到链表头后面,而是根据元素值,找到第一个比T的元素值大的结点,将T插入到其前驱结点的后面,直到P后面没有结点,便可以完成链表的排序了。
假如T指向的结点元素值比P指向的结点元素值更大,那么就不需要再取出T找插入位置了,此时T执行的结点就在正确的位置,我们只需要把P指针后移到T所指的结点即可。按照上述逻辑,编写单向链表排序的实现代码如下:
// datastruct\slist.c
#include - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
上面单向链表排序示例程序的运行结果如下:
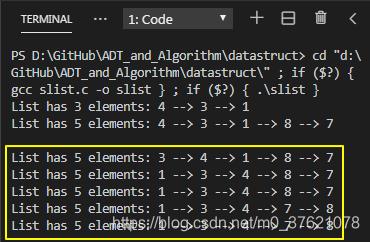
3.3 经典链表操作算法题
| 序号 | LeetCode 算法题 |
|---|---|
| 1 | 206 - 反转链表 |
| 2 | 92 - 反转链表 II |
| 3 | 21 - 合并两个有序链表 |
| 4 | 19 - 删除链表的倒数第N个节点 |
| 5 | 876 - 链表的中间结点 |
| 6 | 234 - 回文链表 |
| 7 | 141 - 环形链表 |
| 8 | 142 - 环形链表 II |
| 9 | 147 - 对链表进行插入排序 |
本章数据结构实现源码下载地址:https://github.com/StreamAI/ADT-and-Algorithm-in-C/tree/master/datastruct


评论记录:
回复评论: