在加密与解密的大战中，RSA加密法取得了暂时的胜利，那它有没有破解法呢？坦率的说，现在还没有，但理论上存在破解的可能，那就是量子计算机和配套的量子算法。

7. 量子加密法

功能齐备的量子计算机到底有多强，我们可以和传统计算机对比来看，不论哪种计算机都是对存储单元中的数据进行操作，比如这个存储单元可以存放N位数据，又因为每个数据都只能是0和1，所以N位数据的存储单元里，数据一共有2^N种可能。传统计算机里，任何一个时刻只能对这么多种可能性中的一个进行操作，当N比较小的时候，工作量还是可以应付的；当N是几千的时候，完成这个工作量需要的时间，就可能会超过全宇宙的历史。

量子计算机中，存储的数据总是处于0和1的叠加态，你可以理解成所有出现0和1的可能性融汇在一起，所以一个量子存储单位某一时刻，是可以同时存储2^N个数据的。比如说这个存储单元有300位，那么存储的数据就是2³⁰⁰比特，这个数字就比全宇宙的原子数还多了。传统计算机要对这么多可能性一个一个操作，而量子计算机运行一次，就是同时对2³⁰⁰个状态进行操作，所以它一次运算的效果相当于2³⁰⁰台传统计算机，算力大大增加。

RSA加密法我们之前也说过，它之所以坚固就是因为要分解一个大数N的因子，这个问题的计算量随N的增加以指数形式增加。但量子计算机一次操作就相当于传统计算机很多次操作，所以如果能设计出一些连续的操作来分解质数的话，即便是一个超大数，用量子计算机也能很快的找出它的因数。这样，RSA加密法就被破解了。

• 量子算法

那这种操作设计出来了吗？已经设计出来了，叫做“Shor算法”，它是1994年设计出来的，专门用于分解因数。一共有7个步骤，其中计算量最大的第4步，是必须在量子计算机中运行的，其它步骤可以在传统计算机中操作。

Shor算法：

1. 选择任意数字a < N
2. 计算gcd(a, N)，这一步是求a和N的最大公约数
3. 若gcd(a, N) ≠ 1，则我们找到了因数，运算结束
4. 否则，找到更小的 r，使ax (mod N) = ax + r (mod N)，根据欧拉定理 r 一定存在，这一步就是需要在量子计算机里实现的步骤
5. 若r是奇数，回到第一步
6. 若ar / 2 ≡ -1 (mod N)，回到第一步
7. gcd(ar/2+1, N)和gcd(ar/2-1, N)分别是N的因数

这是一个专门针对量子计算机设计的算法，它的功能就是专门用来分解因数。Shor算法的作者休尔当年在贝尔实验室做出这个成果后，大致估量了一下算力，他说速度至少可以比传统计算机快百万倍。其实这个差距，是和N的大小选取密切相关的。以当前传统计算机做过的分解因数中最大的数为例，这个数是768位的，传统计算机和量子计算机要计算它，大约是100万年和1秒的差距。

在休尔之后，还是贝尔实验室，洛夫-格鲁夫又设计出一种新算法，也是利用量子计算机，专门针对美国国家标准的加密法DES，结果在当前典型的应用级别下，4分钟就把所有可能的钥匙试遍，密码随之告破。

听起来量子计算机好像很强大，很多谈到量子计算机的新闻都会把它夸张到无以复加的程度，好像传统密码遇到它马上碎成渣。但这种观点是不对的。量子计算机做到的只是大幅削减计算量，其实它还是要花时间计算的，量子计算机很强，但并不是任意一种密码遇到它都秒破。具体来说，针对计算机一个任务所需的时间，有一个评估方法：时间与空间复杂度。传统计算机里，一些像指数级、阶乘级等时间复杂度很高的NP(Non-deterministic Polynomial)问题，在量子计算机中，虽然时间复杂度会大幅下降，但时间复杂度还算高阶。所以我们现在不用那么担心量子计算机出现后，当前的密码保护会瞬间碎成渣渣，只要我们愿意把那个大数n再加长很多，比如从300位增加到3000位，保密强度还是足够应付初期量子计算机破解的。

• 量子计算机

到目前为止，还没有一个通用的量子计算机出现，可靠的专用量子计算机也没有。有人听说过D-Wave这个机器，而且也可能知道武器商洛克希德-马丁2011年就订购过一台128个量子位的量子计算机，但实际上那台D-Wave虽然确实利用量子理论计算，但它只能运行一种特殊的算法，叫做量子退火算法”，所以D-Wave只能算一个实验性质的机器。后来D-Wave还开发了第二代，谷歌和NASA都买过一台，这台改进了很多，是512位的，甚至可以进行一部分传统运算，但是运算速度大约跟1998年前的计算机速度差不多，只是在进行特定的量子算法时才比传统计算机快很多倍。

为什么这么多顶级公司都搞不定量子计算机呢？主要原因就是，量子实在太容易变了，我们现在还没有特别好的手段，能控制量子按照算法的步骤运转。最经典的例子，就是“光的双缝干涉实验”，当我们试图通过一个侦测光子的设备，去观测某一个光子到底是通过哪个缝才射到幕布上时，原先的明暗条纹将会改变，也就是说，我们的测量行为，会影响到量子的状态。

如果双缝干涉实验中的明暗条纹代表着量子计算机运算到某一时刻的量子位的正确状态的话，那设计者要尽最大可能维持住这种状态，但实际上，这种状态会被很多因素干扰，比如对这种状态的观测。在宏观世界里，任何一种物质都有可能和量子发生互动改变他们的状态，比如说温度，所以那些量子计算机，都需要在零下两百多摄氏度的极低温度才能正常工作。

你可能会担心，手中的密码什么时候会受到量子计算机的威胁？至少10年内不用担心，量子计算机的硬件、算法、编程语言、编译器都严重缺失，每一项都是巨大的困难。总有一天量子计算机成熟后，我们现在的密码怎么办呢？由新技术导致的问题，最好的解决方案是更新技术，当量子计算能轻易破解传统加密法后，量子加密也就要诞生了。

• 量子加密法

量子加密和其它加密法最大的不同是，其它加密法的原理只使用了数学，而量子加密不但使用了数学，还使用了物理中的量子理论。也许正是因为背后有两大靠山，所以它是目前为止最强的加密法，就算是量子计算机也很可能无法破解。

量子加密既然是数学和物理结合的产物，那么我们先说说数学原理的部分，数学原理就是我们前面介绍过的单次钥匙簿密码法。如果你还记得，这种加密法无法破解的前提是，要求钥匙完全随机，而这个要求又是几乎不可能在现实中应用的，因为本来真正的随机数就很难获取，退一万步来说，就算有了真正的随机数列，传送钥匙的环节也没法保证完全安全。最保险的方法只能是双方带一堆保镖，当面交换钥匙簿，还得保证保镖里没有特工。而量子加密的无法破解，不仅是理论上无法破解，而且实施过程中还能抵御住绝大部分特工类型的破解。

我们先来介绍下，量子加密是怎样做保密通信的数学过程：

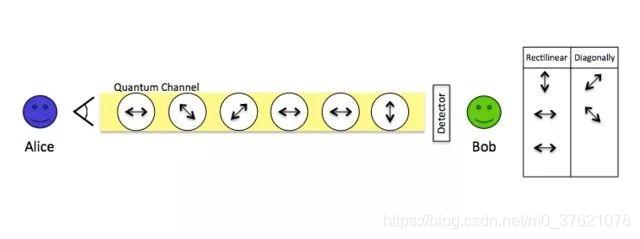
1. 爱丽丝给鲍勃传送一串光子，其中每一位光子信息都用0和1来标注，具体什么算0，什么算1，是有两套测量方法—甲套和乙套，这两种不同的测量方法，对同一个信号的测量结果是不同的；
2. 鲍勃收到光子信息后开始测量，就测量每个光子信息位到底是0还是1。不过鲍勃并不知道爱丽丝那边说的0或者1，到底是按甲方法测的还是乙方法测的。但没关系，鲍勃对每个光子信号都随意选用一套方法来测出每个光子信号到底是0还是1，就可以了。所以鲍勃有时候测出来的结果，肯定是跟爱丽丝发出来的约定相符的，可有时候测出来的结果又是不符的，不过这都没关系，测完了再说；
3. 毕竟鲍勃有一部分是测错的，所以这时候两个人必须打一个电话，这个电话完全不用保密，谁想窃听都可以。爱丽丝和鲍勃在电话里都说什么呢？就是针对每个信号，到底使用了哪套测量方法。这通电话里，就是按照顺位依次说出测量的方法。第一个信号是用甲方法还是乙方法测的，第2个顺位用了甲还是乙方法……所有这些测量方法，由爱丽丝告诉鲍勃；
4. 鲍勃听完爱丽丝的这通电话后，就对照刚刚自己瞎蒙着测的结果，也要回复爱丽丝，回复的具体内容就是，自己哪几位的测量方法蒙对了；
5. 对鲍勃来说，自己之前测错的那些不管，把测对的那几位挑出来，这串数字就可以作为他的钥匙；对爱丽丝来说，因为鲍勃告诉了她哪几位他选对了测量方法，所以爱丽丝也可以把鲍勃选对的那串数字也挑出来，这串数字就可以作为她的钥匙。
   
   两人挑出来的那串数字是完全相等的，而因为完全相等，所以就可以作为两人的钥匙了，它既是鲍勃的钥匙，也是爱丽丝的钥匙。整个过程中，要是并没有在额外的步骤中单独传输，他们在电话里说一说，自己分别回去数一数，就能得到相同的钥匙。之所以钥匙一样，也是数学原理上保证的，咱们不用纠结于数学原理的细节。既然没有单独的钥匙传送环节，所以特工就很难下手。

另外，因为鲍勃和爱丽丝都是随机瞎蒙着选用甲套或乙套两种测量方式的，所以两个人恰巧都用了同一种方法的序列挑出来的数字，也是随机序列，也就是说钥匙是完全随机的。到这里，钥匙既不用额外的传输，而且本身又是完全随机的，这下就满足了单次钥匙簿加密法，并且改进了传送钥匙的薄弱环节，所以实际操作时，可行性就高了很多。就算中间有伊芙窃听了他们的那通电话，伊芙也没法判断到底哪几位应该挑出来当钥匙，因为她不知道鲍勃那边针对每个光子位测量的结果是什么。

现在，还有一种窃听途径，比如说伊芙知道窃听电话没用，那就干脆直接窃听光缆上的信息，这样怎么办呢？这也不用担心。首先，光缆上的信息本来就是单次钥匙薄加密的，就算在使用过程中不遵守随机的原则，暴露了一些特征，也不用担心。因为在量子通信中，还会增加一个确认环节，来判断光路上有没有人窃听。

这是怎么实现的呢？其实就是我们前面说的物理特性。因为人对光子的测量会改变光子原有的量子态，伊芙窃听光缆，其实就相当于在双缝干涉实验时，在两道缝前添加了两个光子探测器，这时候幕布上的明暗条纹就会改变甚至消失。也就是说，爱丽丝和鲍勃只要发现幕布上的图案变了，就知道有人在窃听了。只要发现有人窃听，他们就切换到其他线路上，那条被窃听的线路就废掉了，这是量子加密的一个新功能。

在真实的应用下，伊芙窃听会导致鲍勃收到的信息有错误，但怎么知道有错呢？其实他跟爱丽丝打个电话，核对一下解码出来的原文就可以了。那你说核对原文不就整个都泄密了吗？其实只需要随机从鲍勃收到的消息中，挑选几个字母核对一下是否一致就可以了，只要有一个不对，就说明这条光缆上有特工窃听。

核对的量大概占原文的多少呢？假如从1075个字符里随意挑出75个，如果这75个都是一样的话，基本就能保证这条信息的安全性。为什么说基本呢？因为还存在极小的概率被窃听了，但因为这75个双方都是一致的，所以窃听的概率就大概小于一万亿分之一，还是非常可信的。

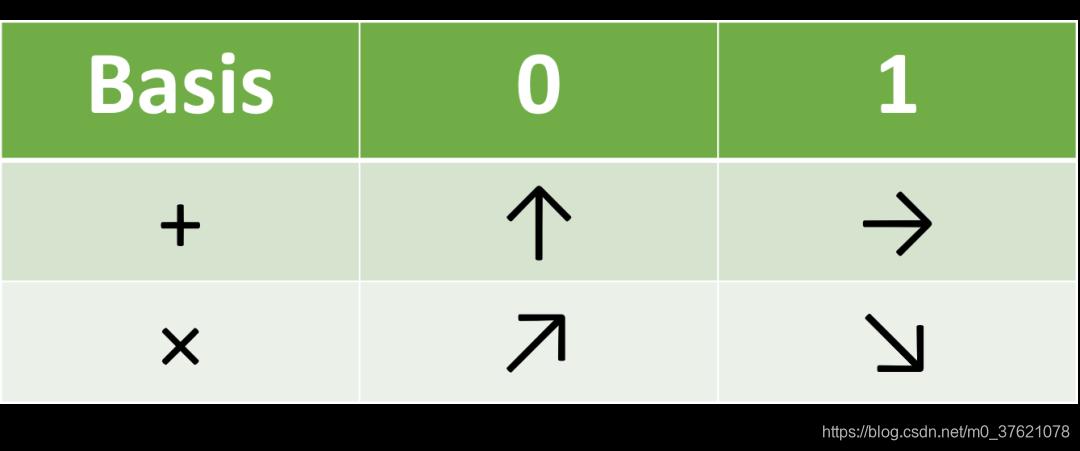
第一次真实的量子加密系统，是1988年在IBM实验室做出来的。它的甲套乙套测量方法，是使用光的偏振方向来呈现量子态，用上下与水平方向偏振代表甲套测量方法（上下振动的光子可以代表0，左右振动的光子则代表1），用45°与135°方向偏振代表乙种测量方法（45°方向的偏振光就代表0，135°方向振动的光子代表1），当时两台计算机只相隔30cm，通信成功了。理论和实践同时胜利，之后的改进主要就体现在两台计算机的通信距离上。

1995年，日内瓦大学可以做到相距23公里，完成量子加密通信。2012年的时候，咱们国家潘建伟团队把这个数字推进到了一百公里这个级别，现在这个团队正在尝试用空间轨道上的卫星和地面接收站间，实现量子加密信息的传输，距离就已经摸到千公里的级别了。

只不过实验中符合条件的光量子态数量实在太少，只有几个到十几个数位，远远不能承载信息的正文，所以到目前为止，量子加密只适合给钥匙加密。

如果你要问，当技术发展到足够的高度，量子加密也会被破解吗？大概率说是破解不了的，因为如果量子加密能被破解，就说明在量子理论中，出现了一种对量子态测量后还不改变量子态的方法，而这是违反量子力学基本原理的。

量子力学是物理学的基本理论，虽说只要是理论，就一定有被证伪的那一天，但这种证伪更可能是一种改进。就像我们先知道地球是个球体，然后才知道赤道方向的直径比南北极方向的直径多了120多公里，也就是说它并不是完美的圆球，而是一个椭球体，只不过椭的太微弱，肉眼看不出来罢了。就是这样一种程度的证伪，而不是某一天突然发现地球是正四面体的那种程度的证伪。这种黑白颠倒的证伪，在量子力学基础理论上是永远不可能发生的。

量子力学的基本理论，是从1905年到今天，被无数实验拷打、锤炼活下来的。如果量子加密可以破解，就说明目前所有量子力学的结论都是错的。

更多文章：

• 《密码学简史（二）— 区块链中的现代密码学》