从计算机时代开始，字母作为操作的最小单位的概念就消失了。在计算机里，所有的数据都被表示成0和1的数字组合（二进制），字母也不例外，把字母数字化得有个标准，现在这个标准就叫做ASCII。字母一旦变成数字，在计算机中字母的符号属性、发音属性等语言规律就完全消失了，它只是一个二进制数字，我们可以随意对它做改变，且这种改变发生在字母内部。所以说，数字化使加密法步入一个新的世代。

5. 对称钥匙：DES加密法

从前恩尼格玛机的时代，德军还会想方设法保密军用版机器的内部结构和使用说明书。但到了计算机时代，所谓内部结构和操作说明根本不用保密，完全公开。到底有多公开呢？

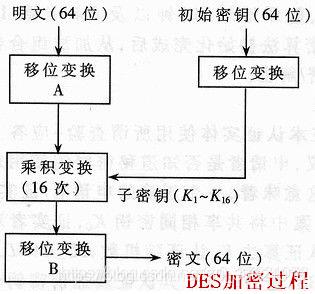
从1976年11月起，有一套规范就成了美国国家标准局的加密系统官方标准，简称DES(Data Encryption Standard)，任何人只要想了解，都可以得到这份规范。这个规范还有个外号—“魔王(Lucifer)”，这是最典型的诞生在计算机时代的第五代密码法。

据说，当初设计者一直把这套算法叫做“示范算法(Demonstration)”，但70年代的操作系统对文件名长度有限制，于是只能截取前几位字母Demon，而Demon又是“恶魔”的意思，后来大家就用另一个恶魔的名字—路西法(Lucifer)，也就是“魔王”来称呼这个算法了。

现在咱们用爱丽丝(Alice)、鲍勃(Bob)、伊芙(Eve)三个人来举例，假如爱丽丝和鲍勃通信，但伊芙想偷听，怎么解决呢？有人说，就使用刚介绍的魔王系统加密嘛，但是信息加密后，钥匙的安全怎么保障呢？

爱丽丝得想法把每条消息对应的钥匙给到鲍勃才行，最稳妥得方法是爱丽丝直接和鲍勃见面，告诉他钥匙内容。你可能会说不用见面，双方约定一下，比如用《独立宣言》的字母顺序当钥匙，就可以省去见面了，但这消息一旦走漏给伊芙，此后两人的通信就没法保密了。所以用魔王系统加密能保证信息主体的安全，但双方还是要交换钥匙，而钥匙的安全是没法保证的，这就是魔王系统最大的漏洞。

对双方约定钥匙内容这件事来说：钥匙越没规律，密码越保险，但也就越需要双方见面沟通；钥匙越有规律，密码越不安全，但却省去了见面沟通的成本。70年代的大银行就专门有个职位，那人每天提着保险箱，飞到世界各地给客户送钥匙。

目前使用最广泛的第五代对称密钥加密法，是由美国国家标准与技术研究院 （NIST）于2001年发布的AES(Advanced Encryption Standard)加密法（可以参考博文：TLS 加密原理），该算法为比利时密码学家Joan Daemen和Vincent Rijmen所设计，结合两位作者的名字，又称Rijndael加密法，是美国联邦政府采用的一种区块加密标准。

现在问题来了：如果是即对安全性要求特别高，又需要频繁沟通该怎么办呢？通过见面沟通交换钥匙的效率显然低得多，要解决这个问题，就要把魔王加密系统的漏洞给补上，也就是在传输加密内容时不必单独传递钥匙，这就需要等到新一代密码系统的诞生了。

6. 非对称钥匙：RSA加密法

6.1 不可逆模运算 — DH密钥交换

用什么方法来避免钥匙的单独传递呢？还得靠数学，具体来说就是用一种不可逆的函数。密码学中为了简单，把它叫做“单向函数”，什么是不可逆函数呢？

数学上有一类特殊的运算–“模运算(modular arithmetic)”，它有时候就是不可逆的。比如 11 * 9 = 8 (mod 13)这个算式，从左往右推可以推出来，而且结果是唯一的，但是从右往左呢，就相当于问你“在模等于13的体系中，什么数乘以9后余数为8？”，这个问题显然不能逆运算，所以“模运算”就是一个单向函数。

明白了模运算，我们就能知道它是怎么用来传递钥匙的了，过程如下：

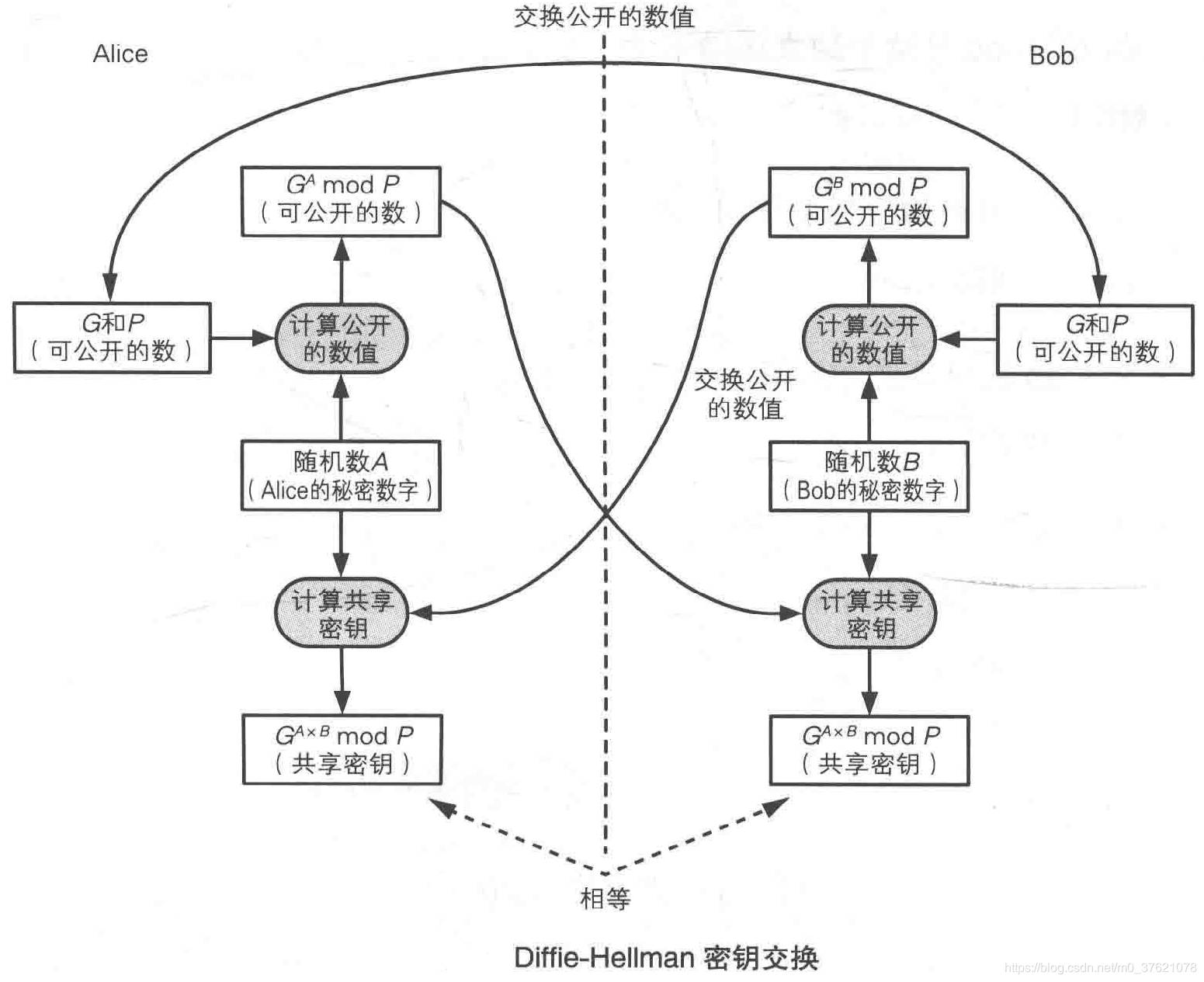
1. 爱丽丝和鲍勃两个人都约定使用G^x mod P函数（G、P要求是质数，比如G = 7、P = 101）；
2. 爱丽丝随便想出一个数A（比如A = 3），鲍勃也随便想出一个数B（比如B = 6)；
3. 他们两个人分别把自己想出来的这个数，代入函数G^x mod P计算一下，比如爱丽丝算完等于α，鲍勃算完等于β；
4. 两人把计算结果告诉对方，直接打电话也行，写信也行，反正是不怕被伊芙偷听的。原因刚刚说过：因为伊芙偷听到的只不过是模运算的结果，而这个结果是不可逆的，所以就算伊芙知道结果，也没法倒推出之前的值；
5. 等爱丽丝和鲍勃都得到对方的结果之后，爱丽丝再做一次β^A mod P运算（也即G^A·B mod P），鲍勃做一次α^B mod P运算（也即G^A·B mod P）。

这两个人算完后，他们将得到完全一样的结果（按上例取值的结果是45）。他们得到的结果相同，那么这个结果就可以当作他们的钥匙。整个过程没人传递过钥匙，但双方都拿到了同样的钥匙。对窃听者伊芙来说，她偷听到的只是模运算的结果，因为这种运算是不可逆的，所以伊芙偷听了也白听。

你可能很困惑，最后两人计算的结果为什么恰恰都等于9？这就是整个过程的精髓所在，不过这可不是巧合，而是sun公司的高级工程师迪菲和斯坦福大学电子系教授黑尔曼两人花了两年多才找到这种函数，因此这套方法被称为“Diffie–Hellman key exchange（迪菲—黑尔曼钥匙交换方案）”。具体的证明过程非常复杂，我们只要知道经过这样的运算，双方都会得到相同的结果就可以了。

6.2 RSA加密法

通过模运算这种不可逆的数学工具，密码学已经发展到不需要单独发送钥匙了。这个突破很大，但它并不实用，因为这套方案有个前提—需要双方一直同时在线，通信才能启动，而现实中像我们用微信、发短信、发邮件一般都不用对方立刻回复，这个应用场景的问题不解决，这套方法就没法商用。

最终实现这个功能的，是第六代密码法—RSA加密法。前五代加密方法如今大多数都不再使用了，而RSA加密法仍是目前使用最广泛的方法，像我们的手机支付加密、网银加密等都会用到它。

RSA这3个字母，分别代表的是它的3位创立者—Ron Rivest、Adi Shamir、Leonard Adleman。下面我们用一个类比来说说RSA加密过程：

1. 爱丽丝有很多把锁，每把锁都有两把不同的钥匙，一把专门用来上锁而不能开锁，另一把专门用来开锁而不能上锁；
2. 爱丽丝把那把用来上锁的钥匙，尽量多的赠送给每个可能和她通信的人，这些人拿到钥匙后，就可以把要跟爱丽丝说的话写下来，再用爱丽丝给的钥匙把锁锁上，然后寄给爱丽丝；
3. 爱丽丝拿到锁好的盒子后，用另一把只有她才有的专用钥匙打开盒子，就可以看到信里的内容了。

这个过程的关键点就是，对同一把锁来说，上锁和开锁用的是两把不同的钥匙，而之前我们介绍的所有加密法都是使用相同钥匙的。所以之前的钥匙都叫“对称钥匙”，而RSA因为使用了不同的钥匙，所以叫“非对称钥匙”或“非对称加密”。

上面用一个比较简单的比喻，把非对称加密过程形容了一下，但类比不能代替理解，实际的思考逻辑是这样的：

1. 爱丽丝要设计出一把公开钥匙，公开是为了让每个人都能复制这把钥匙，用来给自己发信息加密用，但这把钥匙又一定不能解开加密过的信息。所以这一步需要一种不可逆的函数运算，只能加密不能解密，这个可以用前面介绍的模运算实现；
2. 爱丽丝本人还得有一把私人钥匙，它是不公开的，这把钥匙可以解开用她的公开钥匙加密过的信息。

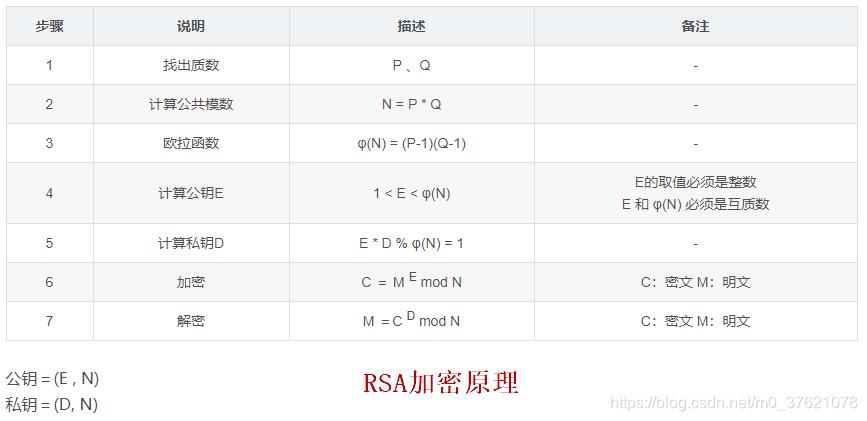
具体的细节比较难懂，需要公式的辅助，这里说一下关键步骤：

1. 爱丽丝展示出来的公开钥匙，是通过两个比较大的素数p和q相乘得到的一个更大的数N得到的。p和q具体是多少，爱丽丝只要自己知道就行，千万不要告诉别人，而乘积N是公开的，谁都可以知道；
2. 凡是要给爱丽丝发消息的人，都需要用N来加密，加密的过程依然用的是模运算，而且模就是N。整个数学过程会保证这个模运算不可逆，所以伊芙就算知道N也没用；
3. 爱丽丝解密时就不需要N了，而是要用到p和q的具体值，而这两个值别人都不知道，只有爱丽丝自己知道。具体来说，爱丽丝私下做的另一个模运算中的模，并不是刚刚我们说的N，而是另外一个值(p-1) x (q-1)，这个公式中就必须要知道p和q到底是多少才行。至于为什么是(p-1) x (q-1)，数学原理会保证这样操作能算出一把新钥匙，这把新钥匙就是爱丽丝自己的私钥，用这把私钥一定可以解出原文。

这样做就能保证安全吗？伊芙已经知道了一个大数N，她难道不能利用精巧的算法，找出N到底是由哪两个大的质数相乘得到的吗？数学保证这是不可能的，N越大，找到p和q两个因数的时间就增加得越夸张。现在银行使用的RSA加密，都要求N是一个超过300位的大数，想分解这样一个数，大约需要把全球计算机的算力集中起来算上几亿年才行。

有人可能会问，为什么非要用两个大的质数相乘呢？用两个巨大的合数相乘得到N，想把这个N的因数找齐，不是也要很久吗？没错，是要很久，但这样做的话，最后算出的私钥也没法解出原文了。所以，找两个质数相乘，也是由数学决定的。

现在我们再来回头看，密码学发展的过程中，公开透明的部分越来越多。到了第六代的RSA加密法，不但加密的操作公开了，连部分钥匙都公开了。而且公钥不是情不得已才公开的，而是越公开益处越大，因为这样才能有更多的人给你发加密消息。到了现在，唯一不能公开的就只有私钥了。

可能你会觉得RSA加密法使用的数学工具很陌生，这个加密法用到了两大数学领域的知识—质数方面的应用与数论有关，单向函数的应用与群论有关。这个算法背后的数学证明，在《算法导论》中有详细论述，如果想深入了解，可以参考这类教材。

6.3 数字签名

前面介绍了RSA非对称加密的原理，不用交换钥匙就能实现信息主体的加密。在现实通信中，保证了通信内容不被窃听就足够了吗？貌似是不行的，因为人们可以不伪造内容，只伪造发信人就行了。比如爱丽丝和伊芙同时追求鲍勃，伊芙可以查一查鲍勃的公钥，然后冒充爱丽丝给鲍勃写信，说自己已经结婚，孩子都好几岁了，这样鲍勃就不会再选择爱丽丝，而会选择伊芙。那鲍勃怎么才能确认这封信确实源自爱丽丝呢？

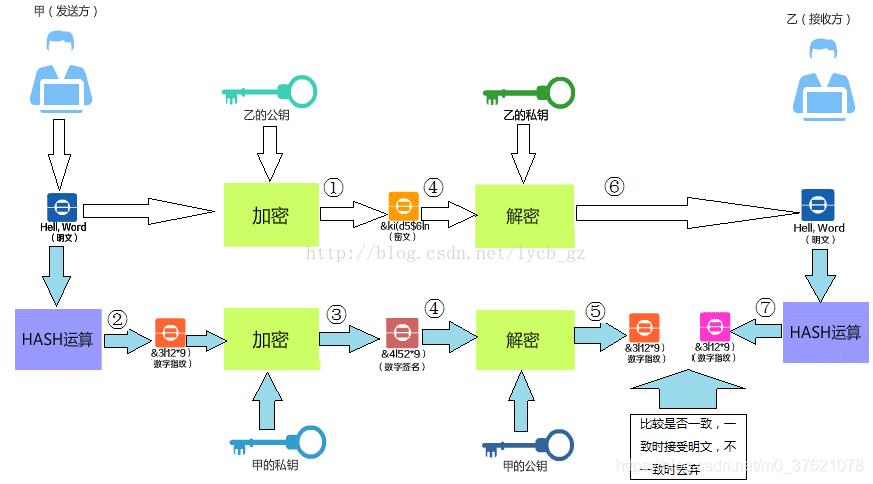
这就要靠数字签名了，计算机中的数字信息没有笔迹，怎么实现数字签名呢？只要把RSA公钥加密私钥解密的过程，反着操作一遍，就可以起到确认身份的功能。本来一条信息应该用公钥加密，私钥解密，但有这样一个事实：在数学上可以保证，加入我们反向操作—用自己的私钥加密信息，而用那把公钥解密的话，也一样可以解开。不过因为爱丽丝的公钥完全是公开的，所以她能解开，其他人也都可以解开，这样加密就很脆弱，但是这个过程正好可以用来确认身份。

如果一条加密过的信息能用爱丽丝的公钥解开，那就说明这条信息当初肯定是用爱丽丝的私钥加密的。世界上谁有爱丽丝的私钥呢？只有她自己。所以凡是这样的信息，就一定证明它来自于爱丽丝，签名的功能就是这样实现的。不过这条信息用公钥就可以解开，谁都可以看，太不安全了，还要再改进下，怎么改进呢？

就是用鲍勃的公钥再加密一次，因为信息是发给鲍勃的，为了只给鲍勃看，所以就用鲍勃的公钥再加一次密。所以，这条消息等于是加了两次密：第一次加密，是为了确保发信人是爱丽丝；第二次加密，是保证只有鲍勃能解开。

当非对称钥匙 + 数字签名，两大功能齐备后，RSA加密就非常实用了。后来真的有人把这两个功能综合到一起，编成软件发布到网上，并引发了90年代整个世界对私人信息保护的大讨论。

最早提供RSA加密的数字签名软件有2个，除了发明了RSA加密法的RSA公司自己外，还有一个软件叫“极佳隐私”，简称PGP(Pretty Good Privacy)，这个PGP是一个叫菲尔–齐玛曼的程序员自己开发的，还是个免费软件。

1980年代，如果一封邮件的内容完全采用RSA加密法，要CPU全力工作几分钟才能完成，这个速度太慢了，如果信息对话似的一条接一条发，CPU根本来不及处理。所以，发明PGP软件的齐玛曼就做了个小调整—信息的主体部分，仍然采用传统的对称钥匙加密（比如AES加密法）。估计你也想到了，对称钥匙的加密过程中，是需要双方传递钥匙的。在传递钥匙的时候，采用非对称钥匙给这个对称钥匙加密（比如RSA加密法），也就是说，给钥匙文再加一把钥匙。因为钥匙文一般比信息原文短小得多，所以这个用计算机处理就轻松多了。而且这个软件把发送钥匙、切换加密法等所有步骤，都设计在后台自动执行，用户根本碰不到，用起来很方便，所以这个软件在互联网上一出现就特别受欢迎。

6.4 比特币中的密码学

现金电子化的想法早在30年前就有了，现在我们用的手机支付就是很实用的现金电子化的例子。但比特币这种电子现金不一样，它的设计初衷是希望在点对点的电子现金支付中，摆脱中央银行的管制。比如说收款和支付都是匿名的，交易不能更改、不能伪造，币的数量有限，不能出现通货膨胀等，所有这些功能都由程序自动保障。既然没有某个机构维护，币又不能伪造，加密技术一定会被用到。

比特币中的密码学并不复杂，只有2种：一个是SHA256加密法；另一个是非对称钥匙系统。SHA256全称是“安全哈希算法(Secure Hash Algorithm)”，哈希是hash的音译，hash就是进行hash函数运算的意思。非对称钥匙就是前面介绍的RSA加密法，或者是RSA加密法的加强版ECC(Elliptic Curve Cryptography)加密法。

• Hash函数

Hash函数是这样，不论原始数据有多长、有多少位，经过Hash运算后，输出的值的长度都是固定的。这有点像图书馆里给图书编号，不论是一个20页的《足球规则手册》，还是1700多页的《资本论》，它们的图书编号都是一个几厘米长的条形码，但这个条形码要派上用场，需要几个先决条件：

1. 任何书不论篇幅长短，都能通过Hash函数计算出唯一一个条形码；
2. 条形码的长度是固定的；
3. 不可能通过条形码，反推出原书的内容。

Hash函数类型很多（常用的如MD5(Message-Digest Algorithm)、SHA1等，效率更高但安全性不如SHA256），比如说比特币中用到的SHA256，256就代表经过函数运算后的结果是一个256位的2进制数字，你可以把它理解为条形码的长度。可能有人要问，怎么可能任何一个数都能运算成一个固定长度的数呢？以十进制来说，假如固定长度是2的话，最多能表示0-99这100个数，遇到103不就没法表示了吗？还记得之前介绍的模运算吧？在模是100的运算中，103 = 3 (mod 100)。而SHA256函数的运算结果，是一个模为2的256次方的值，所以这个值一定是可以写成256位的。

为什么我们要把一个东西转换为一个256位的数字呢？其实最早是为了验证两个文件是否相等而想出来的。举个例子：少林方丈玄慈大师把武功秘籍《易筋经》写成一个程序放到网上供爱好者下载修炼，但玄慈担心有些心术不正的人把这份文件内容偷偷改几个字，故意让练功的人走火入魔。为了防范这个，他就可以把原版《易筋经》通过SHA256运算一下，生成一个值S1，并把S1附到程序中，并提醒大家下载后先做一次SHA256运算，看看运算结果与附上的S1是不是一样的，如果完全一致就说明下载的《易筋经》没有被篡改过，如果不一致就说明被篡改过。

SHA256在验证改动与否这方面，真的挺强。比如下面这3行文字，只是标点上有些微小变化，内容是不变的，但它们对应的SHA256值却差异非常大，一望便知这几条文字肯定是不一样的。原文里微小的不同，就会造成SHA256值巨大的差异，而且这种差异是毫无规律可循的。

原文1：动静不失，人所易明。
S1:	0bc6ba30b4f2a6afa2457d4abd357e53046fc9b433a0845013a5b7c08e9a18f1
原文2：动静不失，人所易明
S2:	ff4cda7e923b68457eb8c31a0b98aae957d223af47032fbcd51b45a44c7edfec
原文3：动静不失人所易明
S3:	529c15a61700d7874ad535be641b8879c554fe4158e7f746d976a958d717ef1c
1
2
3
4
5
6

Hash函数的应用范围远不止安全加密防止篡改这么简单，如果想了解更多Hash算法的应用，可以参考博客：哈希算法能用来干啥？

• 防止篡改与数字签名

你可能会问：Hash函数用在比特币的哪一种功能上了呢？答案是好几处都用到了。

第一处就是支付信息的部分，什么是支付信息呢？比如段誉找薛神医治病后需要付钱，段誉就写了一张付款的纸条，上面写“段誉需要支付100元给薛神医”，这就是支付信息。但这条信息是有风险的，万一有人篡改了内容怎么办？刚刚介绍的SHA256算法就可以避免信息被篡改的问题。“段誉需要支付100元给薛神医”这条信息的SHA256值是确定的，在发出这条支付信息的同时给出SHA256值，之后任何的改动都会被发现。

但只保证了支付信息没有被改动过，这是不够的。如果有心怀不轨的人写出很多条“段誉需要支付1亿元给薛神医”，然后录入支付系统，那段誉可就要哭死了。所以，还需要加上数字签名，它们共同保证了支付信息的内容，不但没被篡改过，而且还是发信人认可的。

如果江湖上每个付钱的人和收款的人都用这种方式记账，把信息都记录在同一个账本上，而且这个账本还是可靠的话，欠债还钱的事儿就说得清了，江湖恩怨也自然少了很多。2007年，有个化名中本聪的人就以这个念头为基础，开发了比特币。

• 余额查验

不过要形成一个可靠的账本，刚刚的过程还是太简单了，还需要增加N种规则，才能让账本系统运作起来。其中最重要的一条就是：段誉支付薛神医100元钱，可是段誉钱包里真的还有那么多钱吗？这个疑问在传统银行系统里不是问题，央行可以查看任何人的账户余额。但中本聪的目的是设计一个没有中央集权的交易系统，也就是大家聊起比特币最常说的“去中心化”的交易系统。在比特币系统中，任何一个参与者和其他参与者有同样高的权限，不存在谁管理谁、谁限制谁，所以余额够不够这一步，只能通过单独的设计。

余额有多少，不能自己说了算，自己说自己还剩多少钱没人信。这一步的解决方案是—每笔交易都必须把以前的交易作为基础。比如“段誉支付100元给薛神医”这笔交易可以进行的前提是，之前有人付给段誉过钱，而且那笔钱不但超过100元，还没使用过。这样段誉支付100元给薛神医，这笔交易才能达成。假如之前曼陀山庄的王夫人已经给过段誉100元了，那么段誉给薛神医付钱时，就会发送标准消息：“王夫人支付100元给段誉，段誉支付100元给薛神医”，然后外加段誉的数字签名和段誉的公钥。薛神医收到标准信息后，该用SHA256确认的确认，该用私钥解锁的解锁，通过一番运算，就可以确认这笔交易了。

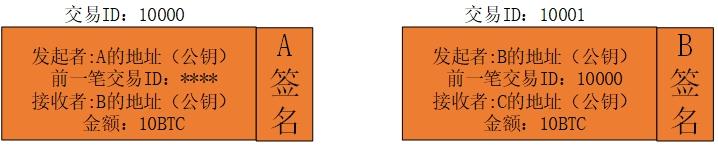
上面举例时用了个特例，就是王夫人之前也正好给过段誉100元，但实际情况不会那么巧，比如王夫人给了段誉500元。在比特币网络中的支付，其实是段誉一次支付给薛神医500元，之后薛神医再自动给段誉支付400元。在比特币网络中，段誉是没法把之前500元那条信息拆分成一个100元和一个400元的，因为这个网络中每个支付信息都由SHA256的签名标记过了，不能再拆分了。之所以这么麻烦，是因为比特币规定了，写入账本的信息必须以之前的交易为基础。之所以要以之前的交易为基础，是因为这套交易系统里没有中央银行。之所以一定要去除中央银行，那就不是技术原因了，而是价值观的问题。

6.5 区块链中的密码学

区块链是什么？简单来说，它是由现代密码学保护，并以串联方式衔接在一起的交易记录。你也可以把它理解成N个账本，每个用户手里都有一份，内容随时更新，但只能添加信息，不能修改信息。理解区块链最好的方式，就是比特币，前面已经介绍了比特币的交易是怎么在密码保护下确认的，下面看看密码学在区块链交易系统中是如何发挥作用的。

在比特币中，所有的转账记录每个电脑都有一份，但要做到这一点可不容易，要解决3个问题：

1. 所有电脑里的账本怎么同步？
2. 怎么防止交易记录被篡改？
3. 怎么防止一笔收入被重复使用？

解决这3个问题的方法就是一个—区块链。区块链之所以叫“链”，体现的就是区块与区块间串联的结构。在区块链中，每一个区块里都包含着成百上千条交易记录，只要经过检验合格了，就写在之前最后一个区块的后面。那都检查什么项目呢？比如交易记录的签名对不对，比特币是不是重复使用了等。

这些检查工作由比特币矿工做，矿工检查合格后，就发送给其他矿工，其他矿工接到新区块也会先检查，如果检查合格，就把这个新区块添加在自己电脑里存储的那条链的最末尾。不过同一时间有N多矿工都在做这件事，他们检查的那些新区块里的内容都是最近刚发生的交易。大概率说，一个新区块里的交易记录大多数是同时到的，但肯定还会略有区别，所以就会面临一个问题—他们会同时向网络提交N个不同版本的新区块。

比特币网络的解决方法是，限制单位时间里产生新区块的数量。比如限制10分钟内只允许产生一个新区块，于是谁先检查完并上传了这个新区块，就以谁的为准。

实际中，这个限制的时间间隔（上面假设的10分钟），是通过让矿工完成两道数学题来保证的。这两道数学题，一个简单，一个复杂，而这里就包含着密码学的部分，而且第一道简单题是区块链之所以能称为“链”的关键。

先说简单题，它是这样计算的：计算出一个字符串，这串字符由3部分组成，第一部分是这个新区块内包含的成百上千的交易记录，第二部分是这个新区块的基本信息，最后一部分是前一个区块的SHA256函数值。三部分综合在一起，就是第一道题的结果，它是一串字符。为什么说这是区块链之所以称为链的重要步骤呢？就是因为当前区块要求包含前一个区块的SHA256函数值，于是区块与区块间就勾连起来了。任何一个区块都包含了它之前所有的历史，所以我们把它称为“链”。

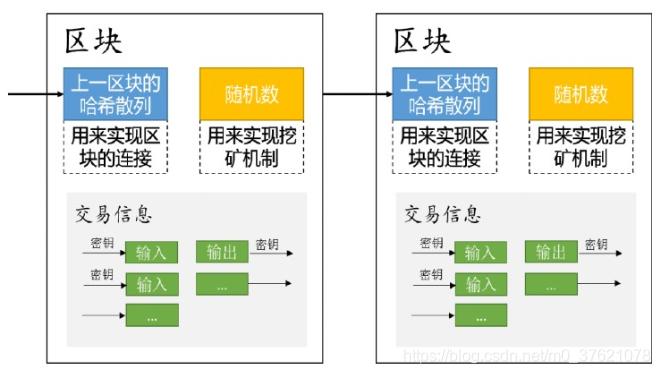
第二道难题一般需要整个比特币网络全部计算机加起来，运算大约十几分钟才能算完。这道题之所以这么难，主要作用就是让提交新区块的人在时间间隔上可以拉开足够长的时间，以免发生刚才说的新区块同时出现的问题。第二道题的题目是第一道题的结果加一个随机数，组成一个新的字符串，这个新字符串用SHA256运算一下，会得到另一个256位的二进制数。但什么才算答案正确呢？得要求这个256位得数字，前72位全部都是0，才算答案正确。

你可能会问：你给我的可是个随机数啊，怎么可能这么巧，算完后前72位都是0呢？是啊，那就的看运气喽。具体要有多好的运气呢？我们可以算一下：第一位是0的概率是1/2，第二位还是0的概率是1/2²，到了第72位仍然是0的概率就是1/2⁷²，也就是说要进行2⁷²次SHA256运算，整个比特币网络中才有一次做对题目的机会，具体是谁做对的说不好，你的算力越强，你的运气就会越好。

前面两道数学题，一旦有人做对了，经过软件检查，新区块就会被放到当前区块链的末尾。对于其他矿工来说，虽然很羡慕，但客户端软件可没有情绪，它们按程序执行，检查新区块是否合格，合格的话就更新到自己的链末尾，整个比特币网络就承认了这个新区块，这就是比特币网络确认新区块的过程。

我们总结下，比特币区块链里的密码学是什么？就是做两道题，一个简单，一个复杂。简单的那个起到的作用是，记录交易信息，再把前后两个区块串联起来；复杂的那个起到的作用是，让每个新区块诞生的时间间隔足够长，以免出现新区块同时产生的情况。不论是哪道题，它们都只使用了SHA256函数，这是一种密码学相关的计算。这些就是区块链上的密码学技术细节，到这里你就能知道，比特币只使用了浅显易懂的密码学应用，并没有发明什么新的加密法。但因为精心的设置，整条链一直运行了10多年。

怎么说是精心的设置呢？咱举个例子，你可能会问：如果计算机性能提升很多，没人用CPU计算第二道难题了，而用速度是CPU几千万倍的专用集成电路(ASIC)做运算，几毫秒就能算出来了，怎么办呢？中本聪规定了，从某个序号的区块后，那个幸运的随机数的要求就变高了，不是前72位是0了，而要求前73位或前74位是0，难度是从前的2倍或4倍，而且这个难度是随着算力增加而增加的，这就保证新区块的生成时间总会有合理的间隔。

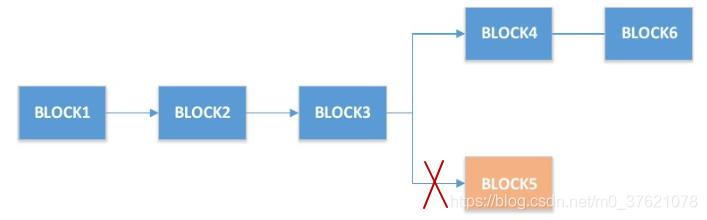
除此之外，就算网络里非常不幸，出现了短短几秒钟诞生2个新区块A和B的情况，还可以通过下个新区块是从A先长出来还是B先长出来 来解决。因为比特币网络还有个规则—整个比特币网络，只认可长度最长的那条链。

这个规则可以防止有人伪造比特币，比如当前进行到B100这个区块了，下一个应该是B101，但有人手工制作出来了另一个区块（交易内容都是给他自己付钱，让他成为富翁的），跟B101不一样，暂且把它叫做M101。这样的伪造极其困难。因为M101后面以M开头的侧链M102区块还得他一个人做，M103也是，可另一条以B开头的主链上B101、B102、B103是全网所有人在做。全网速度远远快于一个人的算力，所以这个人做出的区块链，长度总会比全网主链要短，而刚刚那条规则是—大家只认可最长的那条链，所以这个人即便伪造了交易记录，做出的那条侧链始终得不到认可，所以他没法伪造比特币。只有一种情况下他会得逞，就是他一个人的算力超过所有其他人的算力总和，那时他制作新区块的速度就快过所有人，他做的这条链就会更长，全网就认可他这条链了，但这么做的成本相当高，所以区块链极难伪造。

最后，我们来看区块链的念头是怎么出现的。它不单是从技术细节中长起来的，它是技术加文化观念，一起孕育出来的。技术前面刚刚介绍过，而文化观念就是分权。分权这种念头从古希腊就有，在古希腊人眼中，集权是野蛮的标志，这是西方文化的基石，分权的思想扎根于每个人脑中。一项密码学应用加一种追求分权的念头创造出了区块链，它不一定会挑战现有的体制，但却会给现有的很多难题提供了分权的选择。如果众多分权的协作越来越流行，成为了主流，今后人们合作的模式中就有一部分是由区块链维系的，这就是一种继血缘、民族、法律之后的一种新的人类关系。

更多文章：

• 《Web技术（三）：TLS 加密原理（AES-GCM + ECDHE-ECDSA/RSA）》
• 《密码学简史（一）— 谍战中的古典密码学》
• 《密码学简史（三）— 量子计算中的未来密码学》
• 《【回形针PaperClip】区块链到底是什么？》