前言
虽然我司从23年起,便逐步从教育为主转型到了科技为主,但不代表教育业务便没有了
随着DeepSeek特别是R1、其次V3模型的大火,我司七月在线的大模型线上营群里一学员朋友DIFY问道:校长好,deepseek 的课程目前有多少内容啦,我想要参与学习,想请问一下关于v3和r1复现的课程有吗,不用那么大参数量,小尺寸就好
实话讲,我一开始确实没咋重点考虑R1和V3复现的问题,一来,想着毕竟人家开源了,二来,即便有诸如Open R1这种复现,但效果和原装的相比还是差太多
但后来有三点改变了我的看法
- 对于V3、R1都没有开源他们最核心的训练数据、训练代码
比如V3只是开源了模型权重、模型结构和推理脚本——比如本文前两个部分重点分析的作为推理时实例化模型用的model.py,它的整个文件 中的代码,都只是推理代码 - 虽然Open-R1 只是复现了R1正式版的前两个阶段(如此文所述,R1正式版 有4个阶段)
虽然效果上 不会太好「所以之前没咋关注 因为对于作商用项目的我司来讲,其落地潜力有限」
但毕竟只是一个从零开始的开源小项目 也没法要求太高,所以放到课程中 还是有一定的科研价值的 - 如此,综上可得,或如DIFY所说

加之,我已经 把deepseek各个模型的原理 写透彻了,接下来,确实准备抠下他们已经对外开源的部分代码,然后再带头组织我司部分同事及相关朋友,填补一下无论是V3、R1还是Open R1缺失的代码与流程
以上种种,使得本文来了
- 本文先做第一步:在V3官方代码库MoE、MLA的推理实现之外,补充我个人对多token预测MTP的训练实现(过程中AI打了30%的辅助)
- 下一篇在V3的基础上基于Open R1复现正式版的R1
最后,我特别强调一下,如果对deepseek各类模型及各类算法还不熟悉的话,强烈建议先看对应的原理:《火爆全球的DeepSeek系列模型》,可以看到
- 24年1.5日,DeepSeek LLM发布,没太多创新
类似llama那一套「llama1的RoPE/RMSNorm/SwiGLU + llama2 70B或llama3的GQA」- 24年1.11日,DeepSeekMoE,开启创新之路
提出细粒度专家分割和共享专家隔离,以及一系列负载均衡- 24年1.25,发布DeepSeek-Coder
24年2月,发布DeepSeekMath
提出了Group Relative Policy Optimization(简称GRPO),以替代PPO——舍弃critic模型- 24年5.7日,DeepSeek-V2
提出多头潜在注意力MLA且改进MoE
其中的这个MLA是整个deepseek系列最大的几个创新之一,且由此引发了各大厂商百万token的大幅降价- 24年12.26日,DeepSeek-V3发布
在MoE、GRPO、MLA基础上提出Multi-Token预测,且含FP8训练
大家纷纷把它和Llama 3.1 405B对比,V3以极低的训练成本造就超强的效果,再度出圈- 25年1.20日,DeepSeek R1发布
一方面,提出舍弃SFT、纯RL训练大模型的范式,且效果不错
二方面,性能比肩o1甚至略微超越之
三方面,直接公布思维链且免费,不藏着掖着,相比o1,对用户极度友好
至此爆了,火爆全球总之,原理熟悉之后,再看本文的源码实现,事半功倍——当然,我相信还是有「一帮」朋友就想直接看本文,所以我也在本文中会介绍部分原理,以尽可能让「这帮」朋友可以硬着头皮读下去
第一部分 V3对DeepSeekMoE的推理实现:涉及RoPE、MoE层、Norm层
通过此文《一文通透让Meta恐慌的DeepSeek-V3:在MoE、GRPO、MLA基础上提出Multi-Token预测(含FP8训练详解)》可知,在模型的架构层面,V3主要就在MoE、GRPO、MLA的基础上提出了Multi-Token预测
故先看V3对MoE的实现
根据MoE的结构可知,需要实现Norm层、attention层、MoE层,考虑到V3中的attention是潜在多头注意力——即MLA类实现了多头注意力层,支持低秩查询投影和键值投影,并根据配置选项选择不同的注意力实现,故放到下一部分中介绍(下图来源于Switch Transformers)
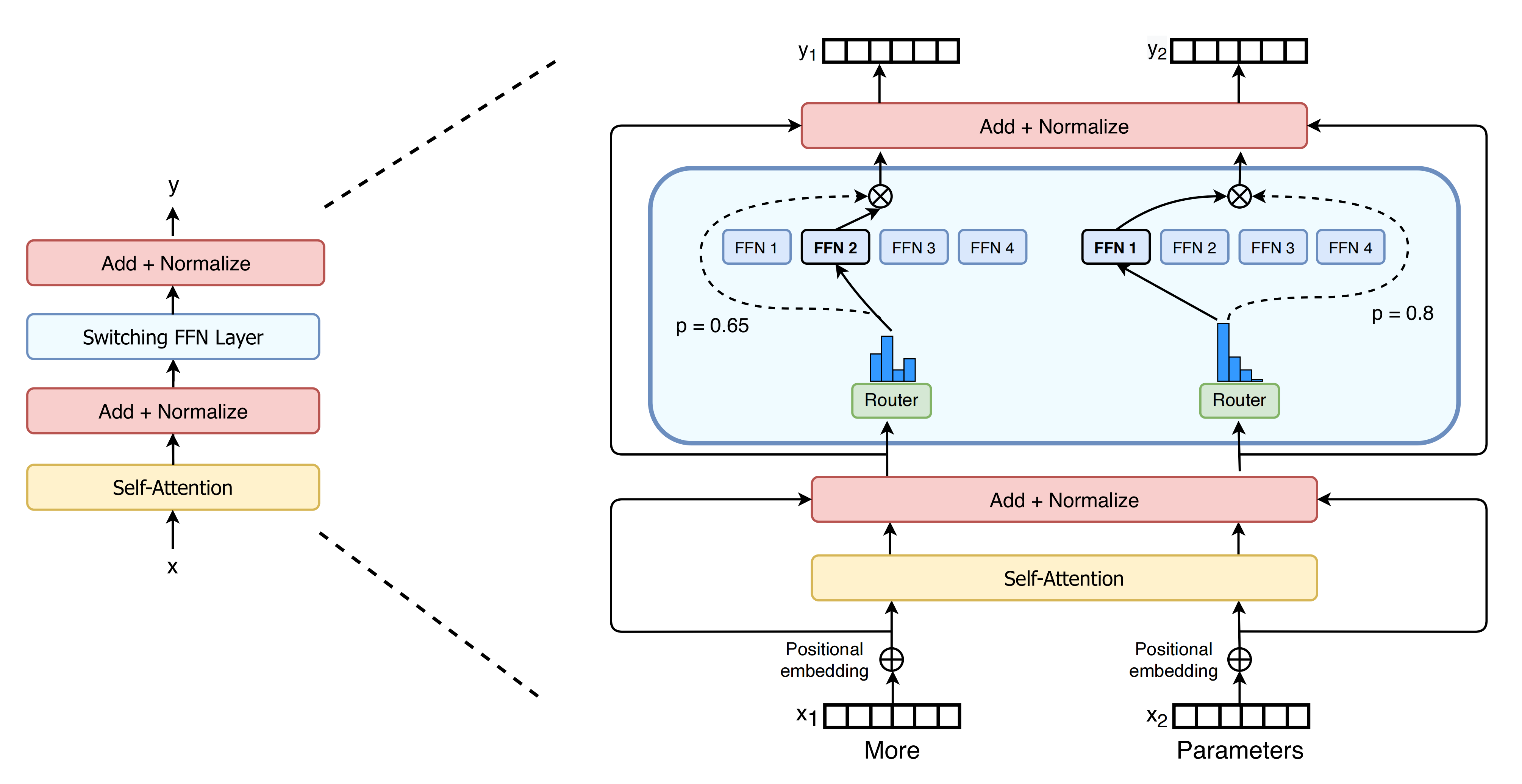
在本第一部分中,我们结合V3代码库中的model.py看下这几个部分的实现
- precompute_freqs_cis函数预计算了用于旋转位置嵌入的频率复数指数值
- apply_rotary_emb函数将旋转位置嵌入应用于输入张量
- MLP类实现了一个多层感知机,用于前馈网络层
- Gate类实现了一个门控机制,用于在专家模型中路由输入
- Expert类实现了专家模型中的专家层
- MoE类实现了专家模型模块,包含多个专家和一个共享专家
- RMSNorm类实现了均方根层归一化,用于对输入张量进行归一化处理
- Block类实现了Transformer块,结合了注意力层和前馈网络层
1.1 RoPE的推理实现
model.py中,关于RoPE的实现涉及以下两个函数
- precompute_freqs_cis函数预计算了用于旋转位置嵌入的频率复数指数值
- apply_rotary_emb函数将旋转位置嵌入应用于输入张量
关于RoPE的更多细节,详见此文《一文通透位置编码:从标准位置编码、旋转位置编码RoPE到ALiBi、LLaMA 2 Long(含NTK-aware简介)》
1.1.1 precompute_freqs_cis函数
precompute_freqs_cis函数用于预计算旋转位置嵌入的基于频率的复数指数值。该函数接收一个ModelArgs类型的参数args,其中包含了位置嵌入的相关参数。函数返回一个预计算的复数指数值的张量,用于位置嵌入
- def precompute_freqs_cis(args: ModelArgs) -> torch.Tensor:
- """
- 预计算用于旋转位置嵌入的基于频率的复数指数值。
- 参数:
- args (ModelArgs): 包含位置嵌入参数的模型参数。
- 返回:
- torch.Tensor: 预计算的用于位置嵌入的复数指数值。
- """
函数首先从args中提取相关参数,包括嵌入维度dim、最大序列长度seqlen、快速和慢速beta修正因子beta_fast和beta_slow、基数base和缩放因子factor
- dim = args.qk_rope_head_dim # 获取查询键旋转嵌入的维度
- seqlen = args.max_seq_len # 获取最大序列长度
- beta_fast = args.beta_fast # 获取快速beta修正因子
- beta_slow = args.beta_slow # 获取慢速beta修正因子
- base = args.rope_theta # 获取旋转位置编码的基数
- factor = args.rope_factor # 获取扩展序列长度的缩放因子
接着,定义了三个辅助函数:find_correction_dim、find_correction_range和linear_ramp_factor
- find_correction_dim函数计算旋转位置嵌入中给定旋转次数的修正维度
它使用输入参数计算修正维度,并返回该值- def find_correction_dim(num_rotations, dim, base, max_seq_len):
- """
- 计算旋转位置嵌入中给定旋转次数的修正维度。
- 参数:
- num_rotations (float): 要计算修正的旋转次数
- dim (int): 嵌入空间的维度
- base (float): 指数计算的基数
- max_seq_len (int): 最大序列长度
- 返回:
- float: 基于输入参数的修正维度
- """
- return dim * math.log(max_seq_len / (num_rotations * 2 * math.pi)) / (2 * math.log(base)) # 计算修正维度
- find_correction_range函数计算旋转位置嵌入的修正维度范围
它接收旋转次数的上下界、嵌入维度、基数和最大序列长度作为参数,返回修正维度的范围- def find_correction_range(low_rot, high_rot, dim, base, max_seq_len):
- """
- 计算旋转位置嵌入的修正维度范围
- 参数:
- low_rot (float): 旋转次数的下界
- high_rot (float): 旋转次数的上界
- dim (int): 嵌入空间的维度
- base (float): 指数计算的基数
- max_seq_len (int): 最大序列长度
- 返回:
- Tuple[int, int]: 修正维度的范围(低,高),并限制在有效索引范围内
- """
- low = math.floor(find_correction_dim(low_rot, dim, base, max_seq_len)) # 计算低修正维度
- high = math.ceil(find_correction_dim(high_rot, dim, base, max_seq_len)) # 计算高修正维度
- return max(low, 0), min(high, dim-1) # 返回修正维度范围
- linear_ramp_factor函数计算用于在最小值和最大值之间平滑值的线性斜坡函数
它返回一个张量,该张量的值在0和1之间线性插值,并限制在[0, 1]范围内- def linear_ramp_factor(min, max, dim):
- """
- 计算用于在最小值和最大值之间平滑值的线性斜坡函数
- 参数:
- min (float): 斜坡函数的最小值
- max (float): 斜坡函数的最大值
- dim (int): 斜坡张量的维度
- 返回:
- torch.Tensor: 形状为(dim,)的张量,值在0和1之间线性插值,并限制在[0, 1]范围内。
- """
- if min == max: # 如果最小值等于最大值
- max += 0.001 # 增加最大值以避免除零错误
- linear_func = (torch.arange(dim, dtype=torch.float32) - min) / (max - min) # 计算线性函数
- ramp_func = torch.clamp(linear_func, 0, 1) # 限制线性函数的值在0到1之间
- return ramp_func # 返回线性斜坡函数
接下来,函数计算频率值freqs,这些值是基于嵌入维度和基数的指数函数。如果序列长度大于原始序列长度,则应用修正范围和平滑因子来调整频率值
- # 计算频率值
- freqs = 1.0 / (base ** (torch.arange(0, dim, 2, dtype=torch.float32) / dim))
- if seqlen > args.original_seq_len: # 如果序列长度大于原始序列长度
- low, high = find_correction_range(beta_fast, beta_slow, dim, base, args.original_seq_len) # 计算修正范围
- smooth = 1 - linear_ramp_factor(low, high, dim // 2) # 计算平滑因子
- freqs = freqs / factor * (1 - smooth) + freqs * smooth # 调整频率值
最后,函数计算时间步长t,并使用外积计算频率值的复数指数表示,返回预计算的复数指数值张量freqs_cis
- t = torch.arange(seqlen) # 生成时间步长
- freqs = torch.outer(t, freqs) # 计算频率值的外积
- freqs_cis = torch.polar(torch.ones_like(freqs), freqs) # 计算频率值的复数指数表示
- return freqs_cis # 返回预计算的复数指数值
1.1.2 apply_rotary_emb的实现
apply_rotary_emb函数用于将旋转位置嵌入应用到输入张量x上。该函数接收两个参数:x是包含位置嵌入的输入张量,freqs_cis是预计算的复数指数值张量,用于位置嵌入
- def apply_rotary_emb(x: torch.Tensor, freqs_cis: torch.Tensor) -> torch.Tensor:
- """
- 将旋转位置嵌入应用于输入张量
- 参数:
- x (torch.Tensor): 包含要应用位置嵌入的输入张量
- freqs_cis (torch.Tensor): 预计算的用于位置嵌入的复数指数值
- 返回:
- torch.Tensor: 应用了旋转嵌入的张量
- """
- 首先,函数保存输入张量的原始数据类型dtype
dtype = x.dtype # 获取输入张量的数据类型 - 然后,将输入张量x转换为浮点类型,并重新调整其形状,使其最后一个维度的大小变为2,以便视为复数
x = torch.view_as_complex(x.float().view(*x.shape[:-1], -1, 2)) # 将输入张量视为复数 - 接着,函数将x视为复数张量函数将freqs_cis调整形状,使其与输入张量的形状匹配。具体来说,freqs_cis的形状调整为(1, 序列长度, 1, 嵌入维度/2),以便在后续计算中进行广播
freqs_cis = freqs_cis.view(1, x.size(1), 1, x.size(-1)) # 调整频率值的形状 - 然后,函数将输入张量x与freqs_cis相乘,得到应用了旋转位置嵌入的复数张量。接着,将结果转换回实数张量,并将其形状调整为原始形状
y = torch.view_as_real(x * freqs_cis).flatten(3) # 计算应用旋转嵌入后的张量 - 最后,函数将结果张量转换回原始数据类型,并返回该张量。这样,输入张量x就应用了旋转位置嵌入
return y.to(dtype) # 返回转换为原始数据类型的张量
1.2 对MoE层的推理实现:包含MLP类、Gate类、Expert类、MoE类
接下来,我们来看MoE的实现
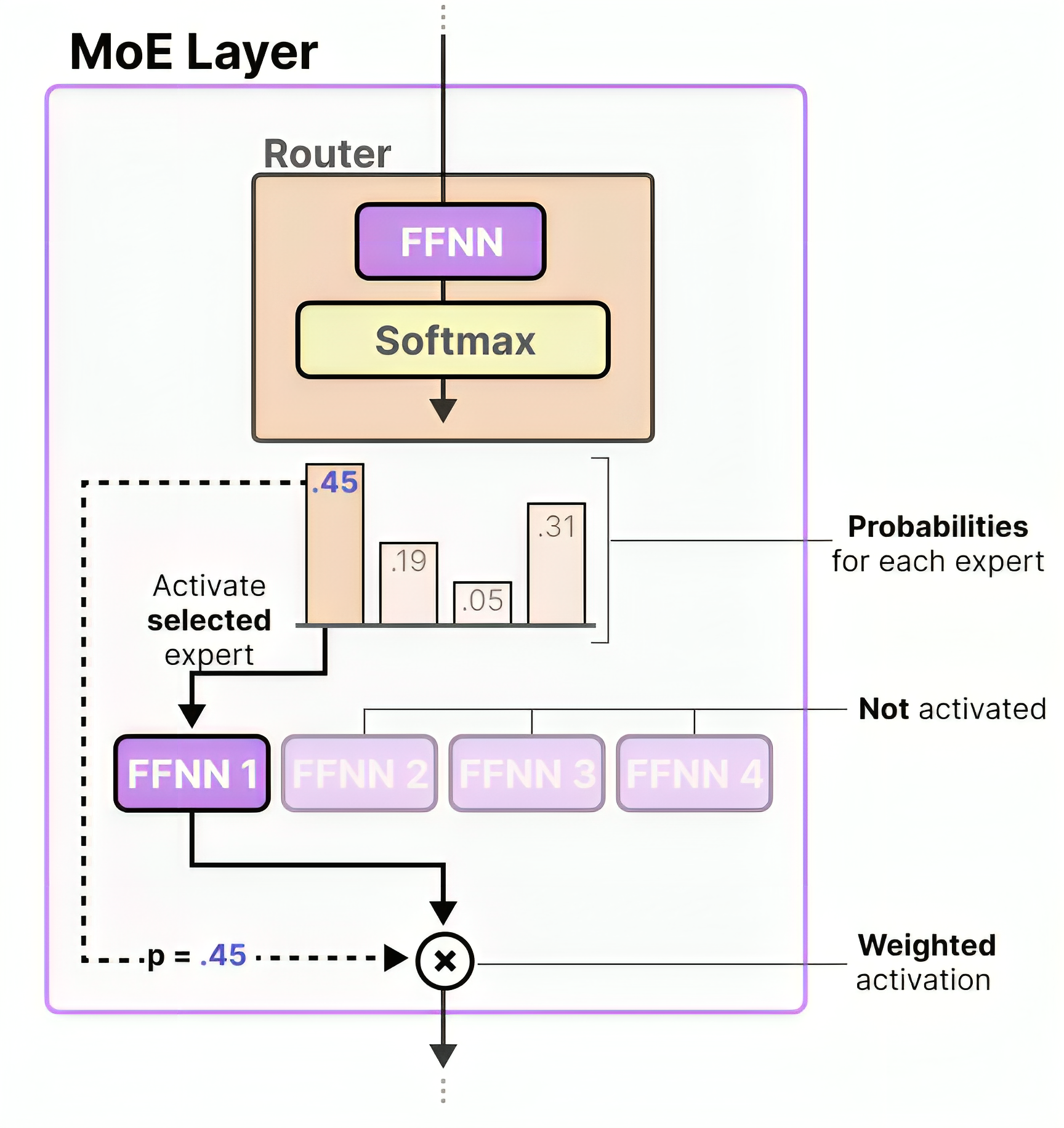
涉及如下这几个函数的实现
- MLP类实现了一个多层感知机,用于前馈网络层
- Gate类实现了一个门控机制,用于在专家模型中路由输入
- Expert类实现了专家模型中的专家层
- MoE类实现了专家模型模块,包含多个专家和一个共享专家
1.2.1 MLP类的实现——多层感知机,用于前馈层
MLP类实现了一个多层感知机(MLP),用于前馈层。该类继承自nn.Module,并包含三个线性层:w1、w2和w3。这些线性层分别用于输入到隐藏层的转换、隐藏层到输出层的转换以及特征转换
- class MLP(nn.Module):
- """
- 多层感知机(MLP),用于前馈层
- 属性:
- w1 (nn.Module): 输入到隐藏层的线性层
- w2 (nn.Module): 隐藏层到输出层的线性层
- w3 (nn.Module): 额外的特征转换线性层
- """
- 在初始化方法__init__中
MLP类接收两个参数:dim表示输入和输出的维度,inter_dim表示隐藏层的维度- def __init__(self, dim: int, inter_dim: int):
- """
- 初始化MLP层。
- 参数
- dim (int): 输入和输出的维度
- inter_dim (int): 隐藏层的维度
- """
w2是行并行线性层(RowParallelLinear),用于将隐藏层维度转换回输入维度- self.w1 = ColumnParallelLinear(dim, inter_dim) # 定义输入到隐藏层的列并行线性层
- self.w2 = RowParallelLinear(inter_dim, dim) # 定义隐藏层到输出层的行并行线性层
- self.w3 = ColumnParallelLinear(dim, inter_dim) # 定义额外的特征转换列并行线性层
1.2.2 门控网络Gate类的实现——输入路由的门控机制
Gate类实现了一个用于混合专家(MoE)模型中的输入路由的门控机制
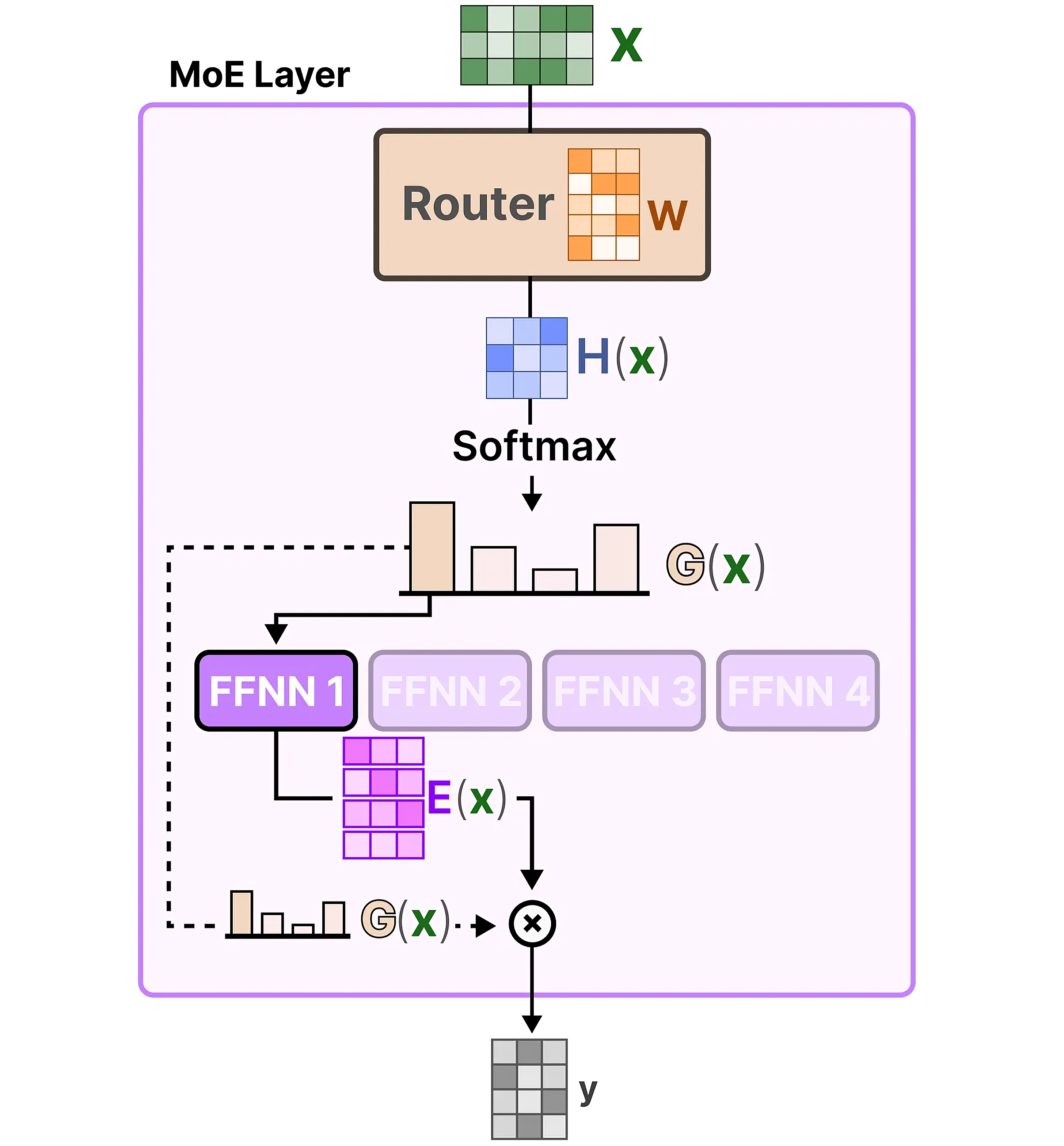
一般就两个计算公式
类似此文《一文速览DeepSeekMoE:从Mixtral 8x7B到DeepSeekMoE(含DeepSeek LLM的简介)》所述,如果每个token选择2个专家,则门控网络的权重矩阵计算对应2个专家的权重,比如w1,w2,然后做softmax,最后与2个专家的输出expert1、expert做加权求和
类似
softmax(X × w1) × expert1 + softmax(X× w2) × expert2
该类继承自nn.Module,并包含多个属性
- class Gate(nn.Module):
- """
- 混合专家(MoE)模型中用于路由输入的门控机制。
- 属性:
- dim (int): 输入特征的维度
- topk (int): 每个输入激活的顶级专家数量
- n_groups (int): 路由组的数量
- topk_groups (int): 路由输入的组数
- score_func (str): 评分函数('softmax'或'sigmoid')
- route_scale (float): 路由权重的缩放因子
- weight (torch.nn.Parameter): 门控机制的可学习权重
- bias (Optional[torch.nn.Parameter]): 门控机制的可选偏置项
- """
- 在初始化方法__init__中,Gate类接收一个ModelArgs类型的参数args,其中包含了门控机制的参数
- def __init__(self, args: ModelArgs):
- """
- 初始化门控模块。
- 参数:
- args (ModelArgs): 包含门控参数的模型参数。
- """
- super().__init__() # 调用父类的初始化方法
- self.dim = args.dim # 设置输入特征的维度
- self.topk = args.n_activated_experts # 设置每个输入激活的顶级专家数量
- self.n_groups = args.n_expert_groups # 设置路由组的数量
- self.topk_groups = args.n_limited_groups # 设置路由输入的组数
- self.score_func = args.score_func # 设置评分函数
- self.route_scale = args.route_scale # 设置路由权重的缩放因子
- self.weight = nn.Parameter(torch.empty(args.n_routed_experts, args.dim)) # 初始化可学习权重
- self.bias = nn.Parameter(torch.empty(args.n_routed_experts)) if self.dim == 7168 else None # 初始化可选偏置项
- 在前向传播方法forward中,Gate类接收一个输入张量x
- def forward(self, x: torch.Tensor) -> Tuple[torch.Tensor, torch.Tensor]:
- """
- 门控机制的前向传播。
- 参数:
- x (torch.Tensor): 输入张量。
- 返回:
- Tuple[torch.Tensor, torch.Tensor]: 路由权重和选择的专家索引。
- """
scores = linear(x, self.weight) # 计算输入张量与权重的线性变换,得到评分- if self.score_func == "softmax": # 如果评分函数是softmax
- scores = scores.softmax(dim=-1, dtype=torch.float32) # 对评分进行softmax归一化
- else:
- scores = scores.sigmoid() # 对评分进行sigmoid归一化
- original_scores = scores # 保存原始评分
- if self.bias is not None: # 如果存在偏置项
- scores = scores + self.bias # 将偏置项加到评分上
- if self.n_groups > 1: # 如果路由组的数量大于1
- scores = scores.view(x.size(0), self.n_groups, -1) # 调整评分的形状
- if self.bias is None: # 如果没有偏置项
- group_scores = scores.amax(dim=-1) # 计算每组的最大评分
- else:
- group_scores = scores.topk(2, dim=-1)[0].sum(dim=-1) # 计算每组前两个评分的和
- indices = group_scores.topk(self.topk_groups, dim=-1)[1] # 选择顶级组的索引
- mask = torch.zeros_like(scores[..., 0]).scatter_(1, indices, True) # 创建掩码
- scores = (scores * mask.unsqueeze(-1)).flatten(1) # 将评分与掩码相乘并展平
1.2.3 Expert类的实现:MoE模型中的专家层
Expert类实现了混合专家(MoE)模型中的专家层。该类继承自nn.Module,并包含三个线性层:w1、w2和w3。这些线性层分别用于输入到隐藏层的转换、隐藏层到输出层的转换以及特征转换。
- class Expert(nn.Module):
- """
- 混合专家(MoE)模型中的专家层
- 属性:
- w1 (nn.Module): 输入到隐藏层的线性层
- w2 (nn.Module): 隐藏层到输出层的线性层
- w3 (nn.Module): 额外的特征转换线性层
- """
- 在初始化方法__init__中,Expert类接收两个参数:dim表示输入和输出的维度,inter_dim表示隐藏层的维度
- def __init__(self, dim: int, inter_dim: int):
- """
- 初始化专家层。
- 参数:
- dim (int): 输入和输出的维度
- inter_dim (int): 隐藏层的维度
- """
- super().__init__() # 调用父类的初始化方法
self.w1 = Linear(dim, inter_dim) # 定义输入到隐藏层的线性层self.w2 = Linear(inter_dim, dim) # 定义隐藏层到输出层的线性层self.w3 = Linear(dim, inter_dim) # 定义额外的特征转换线性层 - 在前向传播方法forward中,Expert类接收一个输入张量x
- def forward(self, x: torch.Tensor) -> torch.Tensor:
- """
- 专家层的前向传播。
- 参数:
- x (torch.Tensor): 输入张量
- 返回:
- torch.Tensor: 经过专家层计算后的输出张量
- """
然后,结果与通过w3线性层的输入张量相乘
最后,乘积通过w2线性层,得到输出张量- # 计算前向传播,应用SiLU激活函数并进行特征转换
- return self.w2(F.silu(self.w1(x)) * self.w3(x))
1.2.4 MoE类:实现了专家模型模块,包含多个专家和一个共享专家
首先,关于什么是共享专家,可以详见此文 《一文速览DeepSeekMoE:从Mixtral 8x7B到DeepSeekMoE(含DeepSeek LLM的简介)》所述
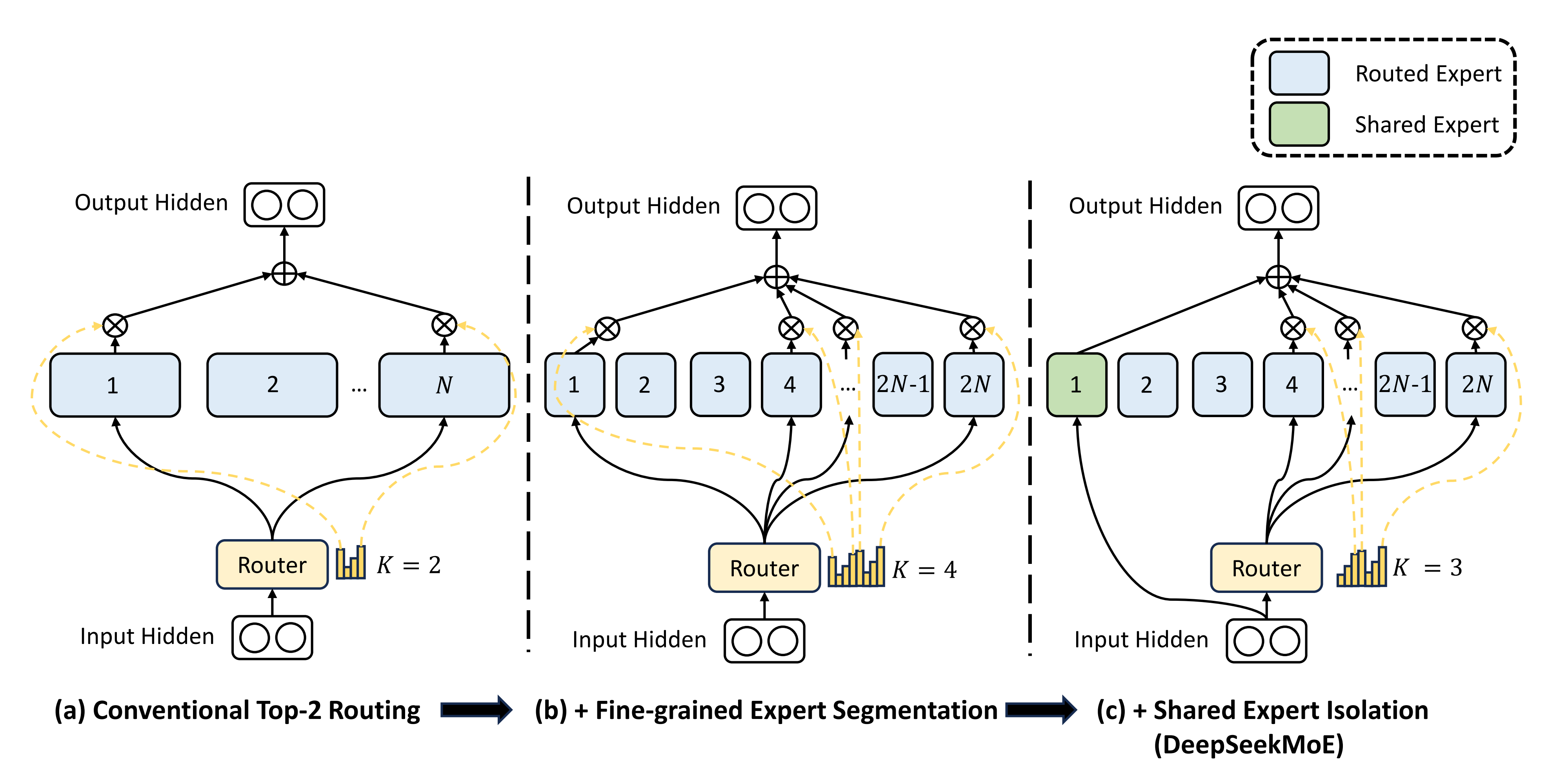
其次,我们来看V3代码库里的model.py中对这一部分的实现
- 首先定义MoE类
- class MoE(nn.Module):
- """
- 混合专家(MoE)模块。
- 属性:
- dim (int): 输入特征的维度。
- n_routed_experts (int): 模型中的专家总数。
- n_local_experts (int): 分布式系统中本地处理的专家数量。
- n_activated_experts (int): 每个输入激活的专家数量。
- gate (nn.Module): 用于将输入路由到专家的门控机制。
- experts (nn.ModuleList): 专家模块列表。
- shared_experts (nn.Module): 应用于所有输入的共享专家。
- """
- 其次,初始化MoE模块
在初始化方法__init__中,MoE类接收一个ModelArgs类型的参数args,其中包含了MoE模块的参数- def __init__(self, args: ModelArgs):
- """
- 初始化MoE模块。
- 参数:
- args (ModelArgs): 包含MoE参数的模型参数
- """
- super().__init__() # 调用父类的初始化方法
- self.dim = args.dim # 设置输入特征的维度
- assert args.n_routed_experts % world_size == 0, f"Number of experts must be divisible by world size (world_size={world_size})" # 确保专家数量可以被世界大小整除
- self.n_routed_experts = args.n_routed_experts # 设置模型中的专家总数
- # 计算本地处理的专家数量
- self.n_local_experts = args.n_routed_experts // world_size
- # 设置每个输入激活的专家数量
- self.n_activated_experts = args.n_activated_experts
- # 计算本地专家的起始索引
- self.experts_start_idx = rank * self.n_local_experts
- # 计算本地专家的结束索引
- self.experts_end_idx = self.experts_start_idx + self.n_local_experts
- # 初始化门控机制
- self.gate = Gate(args)
- self.experts = nn.ModuleList([Expert(args.dim, args.moe_inter_dim) if self.experts_start_idx <= i < self.experts_end_idx else None
- # 初始化专家模块列表
- for i in range(self.n_routed_experts)])
- # 初始化共享专家
- self.shared_experts = MLP(args.dim, args.n_shared_experts * args.moe_inter_dim)
- 最后,前向传播
在前向传播方法forward中,MoE类接收一个输入张量x- def forward(self, x: torch.Tensor) -> torch.Tensor:
- """
- MoE模块的前向传播。
- 参数:
- x (torch.Tensor): 输入张量。
- 返回:
- torch.Tensor: 经过专家路由和计算后的输出张量。
- """
- shape = x.size() # 获取输入张量的形状
- x = x.view(-1, self.dim) # 调整输入张量的形状
- weights, indices = self.gate(x) # 通过门控机制计算路由权重和专家索引
- y = torch.zeros_like(x) # 初始化输出张量
- counts = torch.bincount(indices.flatten(), minlength=self.n_routed_experts).tolist() # 计算每个专家的激活次数
- for i in range(self.experts_start_idx, self.experts_end_idx): # 遍历本地专家
- if counts[i] == 0: # 如果专家没有被激活
- continue # 跳过该专家
- expert = self.experts[i] # 获取专家模块
- idx, top = torch.where(indices == i) # 获取激活该专家的输入索引
- y[idx] += expert(x[idx]) * weights[idx, top, None] # 计算专家输出并加权累加到输出张量
- z = self.shared_experts(x) # 计算共享专家的输出
- if world_size > 1: # 如果是分布式系统
- dist.all_reduce(y) # 聚合所有进程的输出
return (y + z).view(shape) # 返回专家输出和共享专家输出的和,并调整回原始形状
总结一下,这种设计的三个好处是
- 分布式效率:每个进程只负责部分专家的计算,使用all_reduce实现结果同步
- 负载均衡:通过门控机制动态分配计算任务,确保计算资源的高效利用
- 内存优化:使用`None`占位未分配的专家,按需计算,跳过未使用的专家
1.3 Norm层的推理实现:RMSNorm
推理脚本中 还有关于均方根层归一化(RMSNorm)的推理实现
- 首先,定义RMSNorm类
- class RMSNorm(nn.Module):
- """
- 均方根层归一化(RMSNorm)。
- 参数:
- dim (int): 输入张量的维度。
- eps (float): 用于数值稳定性的epsilon值,默认为1e-6。
- """
- 其次,定义__init__方法
- def __init__(self, dim: int, eps: float = 1e-6):
- # 调用父类的初始化方法
- super().__init__()
- # 设置输入张量的维度
- self.dim = dim
- # 设置用于数值稳定性的epsilon值
- self.eps = eps
- # 初始化权重参数,初始值为全1
- self.weight = nn.Parameter(torch.ones(dim))
- 最后,定义forward方法
- def forward(self, x: torch.Tensor):
- """
- RMSNorm的前向传播
- 参数:
- x (torch.Tensor): 输入张量
- 返回:
- torch.Tensor: 归一化后的张量,形状与输入相同
- """
- # 调用F.rms_norm函数进行归一化处理
- return F.rms_norm(x, (self.dim,), self.weight, self.eps)
第二部分 V3对多头潜在注意力MLA的推理代码实现
2.1 对多头潜在注意力MLA原理的回顾
关于对MLA原理的介绍,我已经在这篇《一文通透DeepSeek V2——通俗理解多头潜在注意力MLA:改进MHA,从而压缩KV缓存,提高推理速度》文章中做了详尽、深入、细致的解读
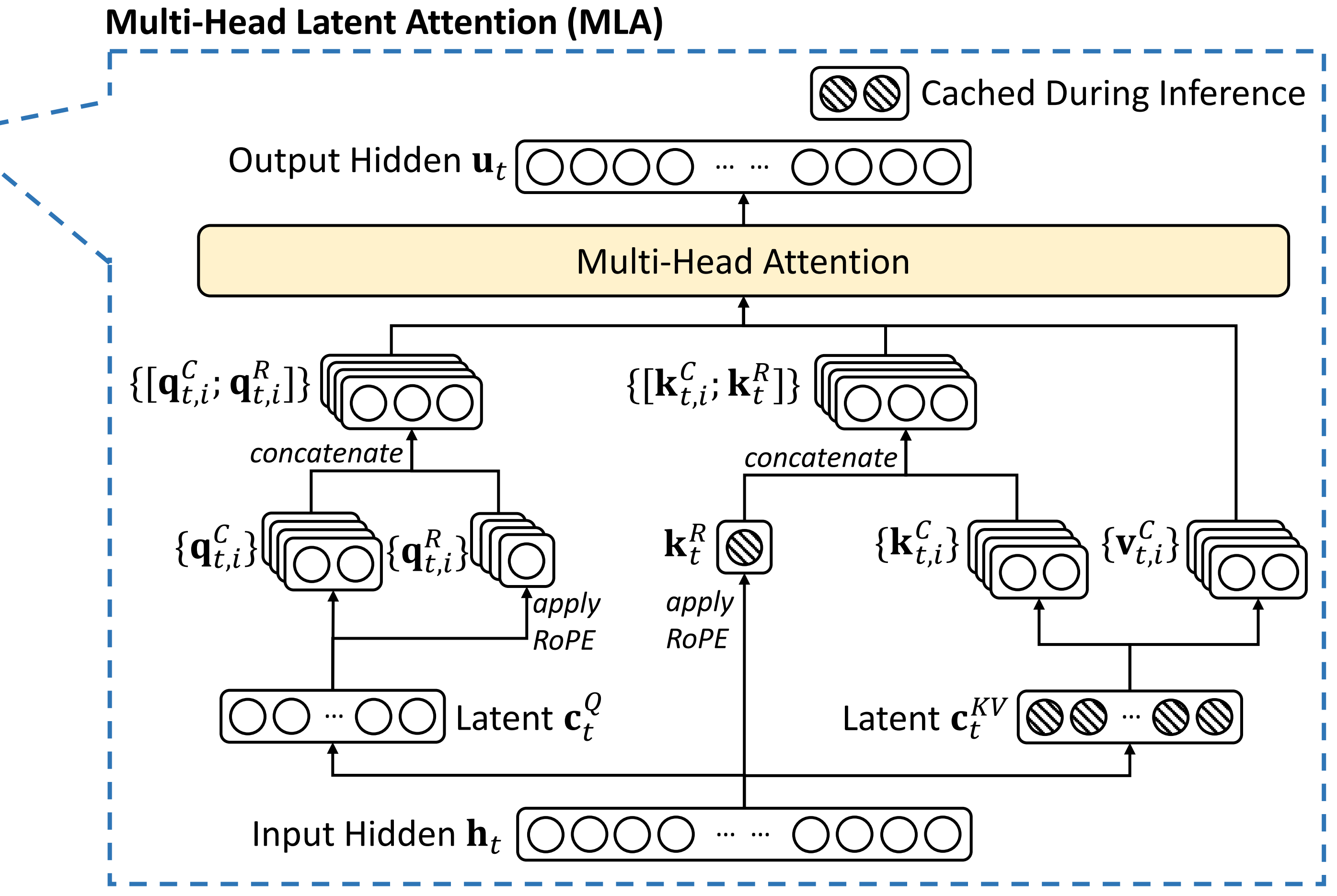
这篇针对MLA的解读,我花了很大的心思、精力,建议好好看看,当你反复琢磨我解读的该文及其中的MLA后,也可以和我一样:脱离v2论文,手绘其图、手推其图背后的公式
2.2 对MLA推理代码的逐行分析
这段代码实现了一个多头注意力层(Multi-Headed Attention Layer, MLA),用于处理输入特征并生成注意力权重
2.2.1 初始化方法__init__的实现
在初始化方法__init__中,类接收一个ModelArgs类型的参数args,其中包含了MLA模块的参数
- def __init__(self, args: ModelArgs):
- super().__init__() # 调用父类的初始化方法
- self.dim = args.dim # 设置输入特征的维度
- self.n_heads = args.n_heads # 设置注意力头的数量
- self.n_local_heads = args.n_heads // world_size # 计算本地处理的注意力头数量
- self.q_lora_rank = args.q_lora_rank # 设置低秩查询投影的秩
- self.kv_lora_rank = args.kv_lora_rank # 设置低秩键值投影的秩
-
- # 设置无位置嵌入的查询键投影的维度
- self.qk_nope_head_dim = args.qk_nope_head_dim
- # 设置旋转位置嵌入的查询键投影的维度
- self.qk_rope_head_dim = args.qk_rope_head_dim
- # 计算查询键投影的总维度
- self.qk_head_dim = args.qk_nope_head_dim + args.qk_rope_head_dim
-
- # 设置值投影的维度
- self.v_head_dim = args.v_head_dim
接下来分别是查询投影、键值投影、输出投影、softmax缩放因子、缓存的初始化
- 查询投影
根据self.q_lora_rank的值选择不同的查询投影实现
这里得解释一下,论文中明明说的要对查询向量做低秩,因为可以降低计算成本,但在具体实现的时候,为何V3官方代码库还允许对查询向量不做低秩呢?
原因很简单,即凡事有利有弊,做低秩的好处是降低计算成本,但不太好的是没法保留更多的特征信息,当然 实际情况一般还是会选择做低秩,毕竟降低成本带来的好处更有用
故才有
 如果self.q_lora_rank为0,则使用ColumnParallelLinear进行查询投影,初始化self.wq
如果self.q_lora_rank为0,则使用ColumnParallelLinear进行查询投影,初始化self.wq - if self.q_lora_rank == 0:
- # 初始化列并行查询投影层
- self.wq = ColumnParallelLinear(self.dim, self.n_heads * self.qk_head_dim)
 否则,先通过Linear进行低秩查询投影,初始化self.wq_a,再通过RMSNorm进行归一化,初始化self.q_norm
否则,先通过Linear进行低秩查询投影,初始化self.wq_a,再通过RMSNorm进行归一化,初始化self.q_norm - else:
- # 初始化低秩查询投影层
- self.wq_a = Linear(self.dim, self.q_lora_rank)
- # 初始化查询投影的归一化层
- self.q_norm = RMSNorm(self.q_lora_rank)
- # 初始化列并行查询投影层
- self.wq_b = ColumnParallelLinear(self.q_lora_rank, self.n_heads * self.qk_head_dim)
- 键值投影
先后通过Linear进行键值投影,初始化self.wkv_a,然后通过RMSNorm进行键值投影归一化,初始化self.kv_norm,最后通过ColumnParallelLinear进行键值投影,初始化self.wkv_b- # 初始化键值投影层
- self.wkv_a = Linear(self.dim, self.kv_lora_rank + self.qk_rope_head_dim)
- # 初始化键值投影的归一化层
- self.kv_norm = RMSNorm(self.kv_lora_rank)
- # 初始化列并行键值投影层
- self.wkv_b = ColumnParallelLinear(self.kv_lora_rank, self.n_heads * (self.qk_nope_head_dim + self.v_head_dim))
- 输出投影
通过RowParallelLinear进行输出投影,初始化self.wo- # 初始化行并行输出投影层
- self.wo = RowParallelLinear(self.n_heads * self.v_head_dim, self.dim)
- Softmax缩放因子
计算Softmax的缩放因子,初始化self.softmax_scale
如果最大序列长度大于原始序列长度,则调整缩放因子- # 计算softmax的缩放因子
- self.softmax_scale = self.qk_head_dim ** -0.5
- if args.max_seq_len > args.original_seq_len:
- # 计算缩放因子
- mscale = 0.1 * args.mscale * math.log(args.rope_factor) + 1.0
- # 调整softmax的缩放因子
- self.softmax_scale = self.softmax_scale * mscale * mscale
- 缓存初始化
根据注意力实现类型(attn_impl),选择不同的缓存策略
如果使用`naive`实现,则初始化键缓存self.k_cache和值缓存self.v_cache——本质就是直接缓存健和值的中间结果- if attn_impl == "naive":
- # 初始化键缓存
- self.register_buffer("k_cache", torch.zeros(args.max_batch_size, args.max_seq_len, self.n_local_heads, self.qk_head_dim), persistent=False)
- # 初始化值缓存
- self.register_buffer("v_cache", torch.zeros(args.max_batch_size, args.max_seq_len, self.n_local_heads, self.v_head_dim), persistent=False)
- else:
- # 初始化键值缓存
- self.register_buffer("kv_cache", torch.zeros(args.max_batch_size, args.max_seq_len, self.kv_lora_rank), persistent=False)
- # 初始化位置嵌入缓存
- self.register_buffer("pe_cache", torch.zeros(args.max_batch_size, args.max_seq_len, self.qk_rope_head_dim), persistent=False)
总之,MLA这套初始化的设计,可以
- 通过列并行和行并行的线性层,实现分布式计算。
- 支持低秩查询投影和键值投影,适应不同的模型配置
- 根据注意力实现类型,选择不同的缓存策略,减少内存占用
2.2.2 前向传播方法forward方法的实现
在前向传播方法forward中,其接收输入张量,并通过一系列计算生成输出张量
- def forward(self, x: torch.Tensor, start_pos: int, freqs_cis: torch.Tensor, mask: Optional[torch.Tensor]):
- """
- Multi-Headed Attention Layer (MLA) 的前向传播
- 参数:
- x (torch.Tensor): 输入张量,形状为 (batch_size, seq_len, dim)
- start_pos (int): 序列中用于缓存的起始位置
- freqs_cis (torch.Tensor): 预计算的旋转位置嵌入的复数指数值
- mask (Optional[torch.Tensor]): 可选的掩码张量,用于排除某些位置的注意力计算
- 返回:
- torch.Tensor: 输出张量,形状与输入相同
以下是对这段代码的详细解读:
- 输入张量的形状
获取输入张量的批次大小 (bsz)、序列长度 (seqlen) 和特征维度 (_)
计算序列的结束位置 (end_pos)- # 获取输入张量的批次大小、序列长度和特征维度
- bsz, seqlen, _ = x.size()
- # 计算序列的结束位置
- end_pos = start_pos + seqlen
- 查询投影
根据 q_lora_rank 的值选择不同的查询投影实现——至于为何这么做的原因,上文已经说明过了,故此处不再赘述
如果 q_lora_rank为 0,则使用 wq 进行查询投影,否则,先通过 wq_a 进行低秩查询投影,再通过 q_norm 进行归一化,最后通过 wq_b 进行查询投影- # 根据 q_lora_rank 的值选择不同的查询投影实现
- if self.q_lora_rank == 0:
- # 使用全秩投影
- q = self.wq(x)
- else:
- # 使用低秩投影
- q = self.wq_b(self.q_norm(self.wq_a(x)))
且对其中的旋转位置嵌入部分q_pe:应用旋转位置嵌入 (apply_rotary_emb)- # 将查询投影结果调整为四维张量
- q = q.view(bsz, seqlen, self.n_local_heads, self.qk_head_dim)
- # 拆分查询投影结果为无位置嵌入部分和旋转位置嵌入部分
- q_nope, q_pe = torch.split(q, [self.qk_nope_head_dim, self.qk_rope_head_dim], dim=-1)
- # 对旋转位置嵌入部分应用旋转位置嵌入
- q_pe = apply_rotary_emb(q_pe, freqs_cis)
- 键值投影
通过 wkv_a进行键值投影,并拆分为键值部分 (kv) 和旋转位置嵌入部分 (k_pe)
并对其中的旋转位置嵌入部分k_pe:应用旋转位置嵌入 (apply_rotary_emb)- # 进行键值投影
- kv = self.wkv_a(x)
- # 拆分键值投影结果为键值部分和旋转位置嵌入部分
- kv, k_pe = torch.split(kv, [self.kv_lora_rank, self.qk_rope_head_dim], dim=-1)
- # 对旋转位置嵌入部分应用旋转位置嵌入
- k_pe = apply_rotary_emb(k_pe.unsqueeze(2), freqs_cis)
- 注意力计算
根据注意力实现类型 (attn_impl),选择不同的注意力计算方法
 如果使用 `naive` 实现:
如果使用 `naive` 实现:
将查询的无位置嵌入部分和旋转位置嵌入部分拼接
通过 wkv_b进行键值投影归一化
将键值投影结果调整为四维张量,并拆分为键值部分 (k_nope) 和值部分 (v)
将键值部分和旋转位置嵌入部分拼接,并缓存键值和值
计算查询和键值的点积,得到注意力得分 (scores)- # 根据注意力实现类型选择不同的注意力计算方法
- if attn_impl == "naive":
- # 将查询的无位置嵌入部分和旋转位置嵌入部分拼接
- q = torch.cat([q_nope, q_pe], dim=-1)
- # 进行键值投影归一化
- kv = self.wkv_b(self.kv_norm(kv))
- # 将键值投影结果调整为四维张量
- kv = kv.view(bsz, seqlen, self.n_local_heads, self.qk_nope_head_dim + self.v_head_dim)
- # 拆分键值投影结果为键值部分和值部分
- k_nope, v = torch.split(kv, [self.qk_nope_head_dim, self.v_head_dim], dim=-1)
- # 将键值部分和旋转位置嵌入部分拼接
- k = torch.cat([k_nope, k_pe.expand(-1, -1, self.n_local_heads, -1)], dim=-1)
- # 缓存键和值
- self.k_cache[:bsz, start_pos:end_pos] = k
- self.v_cache[:bsz, start_pos:end_pos] = v
- # 计算查询和键的点积,得到注意力得分
- scores = torch.einsum("bshd,bthd->bsht", q, self.k_cache[:bsz, :end_pos]) * self.softmax_scale
 否则:
否则:
对键值投影结果进行权重反量化,并调整为三维张量
计算查询和键值的点积,得到注意力得分 (scores)- else:
- # 对键值投影结果进行权重反量化
- wkv_b = self.wkv_b.weight if self.wkv_b.scale is None else weight_dequant(self.wkv_b.weight, self.wkv_b.scale, block_size)
- # 调整为三维张量
- wkv_b = wkv_b.view(self.n_local_heads, -1, self.kv_lora_rank)
- # 计算查询和键的点积
- q_nope = torch.einsum("bshd,hdc->bshc", q_nope, wkv_b[:, :self.qk_nope_head_dim])
- # 缓存键值
- self.kv_cache[:bsz, start_pos:end_pos] = self.kv_norm(kv)
- # 缓存位置嵌入
- self.pe_cache[:bsz, start_pos:end_pos] = k_pe.squeeze(2)
- # 计算注意力得分
- scores = (torch.einsum("bshc,btc->bsht", q_nope, self.kv_cache[:bsz, :end_pos]) +
- torch.einsum("bshr,btr->bsht", q_pe, self.pe_cache[:bsz, :end_pos])) * self.softmax_scale
- 掩码应用
如果存在掩码张量,则将其加到注意力得分上- # 如果存在掩码张量,则将其加到注意力得分上
- if mask is not None:
- scores += mask.unsqueeze(1)
- 注意力权重计算
对注意力得分应用 softmax- # 对注意力得分应用softmax
- scores = scores.softmax(dim=-1, dtype=torch.float32).type_as(x)
 如果使用 `naive` 实现,属于直接实现的注意力机制,计算简单,但在大规模数据上效率偏低
如果使用 `naive` 实现,属于直接实现的注意力机制,计算简单,但在大规模数据上效率偏低
计算注意力权重和值的点积,得到输出张量- # 根据注意力实现类型计算输出张量
- if attn_impl == "naive":
- # 计算注意力权重和值的点积
- x = torch.einsum("bsht,bthd->bshd", scores, self.v_cache[:bsz, :end_pos])
 否则:考虑优化过的注意力机制,比如低秩注意力
否则:考虑优化过的注意力机制,比如低秩注意力
计算注意力权重和键值的点积,再计算与值的点积,得到输出张量- else:
- # 计算注意力权重和键值的点积
- x = torch.einsum("bsht,btc->bshc", scores, self.kv_cache[:bsz, :end_pos])
- # 计算与值的点积
- x = torch.einsum("bshc,hdc->bshd", x, wkv_b[:, -self.v_head_dim:])
- 输出投影
通过 wo 进行输出投影,计算最终输出张量,并返回- # 进行输出投影
- x = self.wo(x.flatten(2))
- # 返回最终输出张量
- return x
第三部分 我个人对多token预测MTP的训练代码实现:严格按照V3技术报告来
比较遗憾的是,V3官方代码库里 并没有对MTP技术的完整实现
- 如我司大模型同事阿荀所说,MTP只是属于训练期间设定的损失函数和额外结构,官方没有提供训练代码,这里边应该也意味着不提供MTP的实现
- meta 倒是有个mtp实现,但如此文 《一文通透让Meta恐慌的DeepSeek-V3:在MoE、GRPO、MLA基础上提出Multi-Token预测(含FP8训练详解)》的「1.2.3 多token预测:Multi-Token Prediction——显著加快模型的解码速度」的开头所说
“受Gloeckle等人「其对应的论文为《Better & Faster Large Language Models via Multi-token Prediction》,这是由Meta团队发在ICML 2024的一篇Poster」的启发,他们为DeepSeek-V3研究并设置了一个多token预测(MTP)目标,该目标将预测范围扩展到每个位置的多个未来token”
相当于ds的mtp实现和meta的mtp实现 有点区别
故咱们得自己来实现下,但实现的过程中要尽可能和V3官方代码库的风格一致——毕竟 我们最终希望可以实地用起来,避免只是做个示例展示而已
3.1 对多token预测MTP原理的回顾
实现之前,首先通过此文《一文通透让Meta恐慌的DeepSeek-V3:在MoE、GRPO、MLA基础上提出Multi-Token预测(含FP8训练详解)》的「1.2.3 多token预测:Multi-Token Prediction——显著加快模型的解码速度」来回顾下MTP的核心原理
3.1.1 对MTP核心原理的理解
我个人觉得啊,无论是V3技术报告中,还是Gloeckle等人(2024年)原始论文中对Multi-Token Prediction的描述对初学者都不友好,很容易看晕——就快到谁看谁晕乎的程度了,我一开始看 也晕乎了一会,为了更好的理解,我还是给大家举个例子吧
据我所知,截止到25年1.7日之前,下面这个例子在全网也是首例了,过程中还和同事阿荀做了深入的讨论/确认
比如下图所示,完整序列是t1-t7,当前主模块考虑的输入序列为t1,t2,t3,t4,然后预测t5,t6,t7
由于当
时,
指的是由主模型给出的表示,故有
对于输入token t1,主模型生成表示
对于输入token t2,主模型生成表示
对于输入token t3,主模型生成表示
对于输入token t4,主模型生成表示
- 对于MTP Module 1的预测(注,是如下图第2个模块所示),k = 1
并t2预测t3(或者说,t2辅助
预测t3)
并t3预测t4(或者说,t3辅助
预测t4)
并t4预测t5
并t5预测t6
根据公式21(记住一点,
的下标
永远和主模型的输入下标一致,即
一直等于1 或2 或3 或4)
可以得到各个token的输入表示
将 t1的主模型表示和 t2 的嵌入 Emb(t2)结合,通过公式 21 计算得到
将 t2的主模型表示 和 t3 的嵌入 Emb(t3)结合,通过公式 21 计算得到
将 t3的主模型表示和 t4 的嵌入 Emb(t4)结合,通过公式 21 计算得到
将 t4的主模型表示和 t5 的嵌入 Emb(t5)结合,通过公式 21 计算得到
根据公式22,可得,对于transformer处理
将输入到 Transformer 块 TRM1 中,得到
将输入到 Transformer 块 TRM1 中,得到
将输入到 Transformer 块 TRM1 中,得到
将输入到 Transformer 块 TRM1 中,得到
根据公式23,可得,对于输出头预测
将 输入到输出头 OutHead 中,得到 t3 的预测概率
将 输入到输出头 OutHead 中,得到 t4 的预测概率
将输入到输出头 OutHead 中,得到 t5 的预测概率
将输入到输出头 OutHead 中,得到 t6 的预测概率
对于MTP Module 2的预测(注,如下图第3个模块所示),k = 2
并t3预测t4(或者说,t3辅助
预测t4)
并t4预测t5
并t5预测t6
并t6预测t7
输入表示:
将 和 t3 的嵌入 Emb(t3) 结合,通过公式 21 计算得到
将 和 t4 的嵌入 Emb(t4) 结合,通过公式 21 计算得到
将 和 t5 的嵌入 Emb(t5) 结合,通过公式 21 计算得到
将 和 t6 的嵌入 Emb(t6) 结合,通过公式 21 计算得到
Transformer 处理:
将输入到 Transformer 块 TRM2 中,得到
将输入到 Transformer 块 TRM2 中,得到
将输入到 Transformer 块 TRM2 中,得到
将输入到 Transformer 块 TRM2 中,得到
输出头预测:
将 输入到输出头 OutHead 中,得到 t4 的预测概率
将 输入到输出头 OutHead 中,得到 t5 的预测概率
将 输入到输出头 OutHead 中,得到 t6 的预测概率
将 输入到输出头 OutHead 中,得到 t7 的预测概率
我们再把上面这整个过程
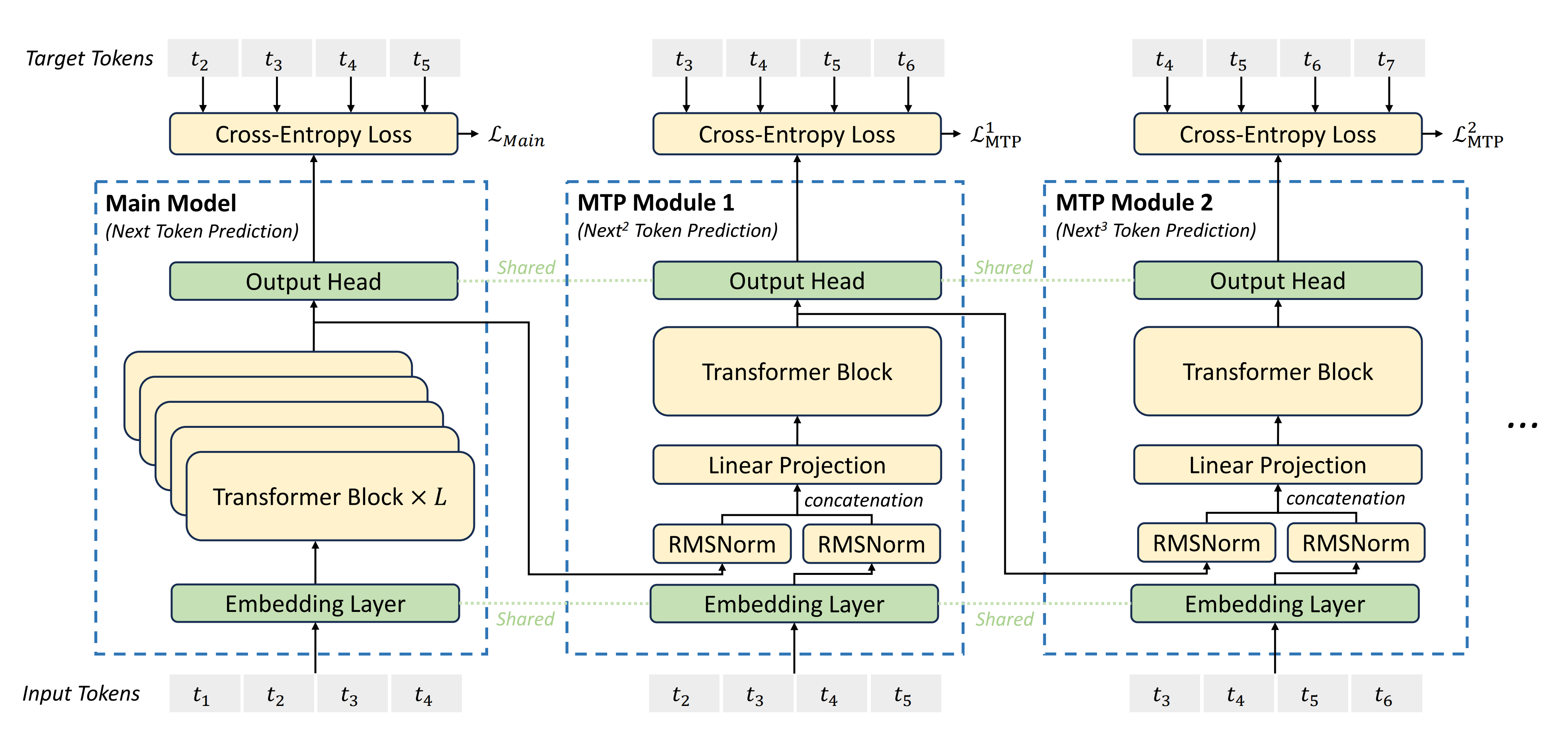
弄到一个统一的大表格里下,以示一目了然
| 主模型表示 | 对于MTP Module 1的预测(注,是如下图第2个模块所示),k = 1 | 对于MTP Module 2的预测(注,如下图第3个模块所示),k = 2 |
| 由于当 对于输入token t1,主模型生成表示 对于输入token t2,主模型生成表示 对于输入token t3,主模型生成表示 对于输入token t4,主模型生成表示 | 输入表示 | 输入表示: |
| Transformer 处理: | Transformer 处理: | |
| 输出头预测: 将 | 输出头预测: |
3.1.2 MTP的训练目标
对于每个预测深度,他们计算一个交叉熵损失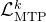 :
:
![\mathcal{L}_{\mathrm{MTP}}^{k}=\operatorname{CrossEntropy}\left(P_{2+k: T+1}^{k}, t_{2+k: T+1}\right)=-\frac{1}{T} \sum_{i=2+k}^{T+1} \log P_{i}^{k}\left[t_{i}\right]](https://img1.iyenn.com/thumb02/c4a7c4f8a7c4b25d/356117394547807393774.jpeg%3D%5Coperatorname%7BCrossEntropy%7D%5Cleft%28P_%7B2+k%3A%20T+1%7D%5E%7Bk%7D%2C%20t_%7B2+k%3A%20T+1%7D%5Cright%29%3D-%5Cfrac%7B1%7D%7BT%7D%20%5Csum_%7Bi%3D2+k%7D%5E%7BT+1%7D%20%5Clog%20P_%7Bi%7D%5E%7Bk%7D%5Cleft%5Bt_%7Bi%7D%5Cright%5D)
其中T 表示输入序列长度,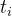 表示第
表示第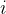 个位置的真实token,
个位置的真实token,![P_{i}^{k}\left[t_{i}\right]](https://img1.iyenn.com/thumb02/c4a7c4f8a7c4b25d/789617394547803557.jpeg) 表示由第k 个MTP 模块给出的
表示由第k 个MTP 模块给出的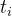 的相应预测概率
的相应预测概率
最后,他们计算所有深度上的MTP 损失的平均值,并将其乘以一个权重因子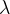 ,以获得总体MTP 损失
,以获得总体MTP 损失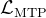 ,这作为DeepSeek-V3 的附加训练目标
,这作为DeepSeek-V3 的附加训练目标

3.2 对MTP技术的多轮实现——coding By July和AI
3.2.1 小试牛刀:先做一轮简单实现
正如R1解答用户问题之前,会先经过一轮长时间的推理/思考、拆解/分析,而这个推理/思考的过程,可以很好的帮助很多人提高分析问题、解决问题的能力
为了更好的和大家一块成长,我也没必要一上来就给大家一个完美的实现——毕竟所有的强大与伟大都不是一蹴而就的 包括2年多前的ChatGPT以及本文的R1(看本文开头便知,R1发布之前,deepseek已经经历了不少大大小小的创新)
- 那就先小试牛刀,先不考虑V3已有的官方代码库,先对MTP做一轮简单的实现,以让对原理有个更好的了解「当我们对原理有更好的理解,然后对V3官方代码库已有的结构有更好的研究之后,我们便能写出完美匹配官方库的实现 」
- 过程中有30%的部分得到了AI的辅助,相当于代码是由我个人和AI完成的
具体步骤如下
- 引入相关库
- import torch
- import torch.nn as nn
- from transformers import RMSNorm
- class MTPModule(nn.Module):
先做初始化——注意,这里暂时没考虑V3的MoE架构,而是简单粗暴的先暂用标准的transformer架构,即我先故意一切从简,但下一节会修改
- def __init__(self, d_model, vocab_size, num_layers, n_head):
- super().__init__()
- # 预测深度
- self.D = num_layers
- // 从主模型共享嵌入、输出头
- self.shared_emb = nn.Embedding(vocab_size, d_model)
- self.shared_out = nn.Linear(d_model, vocab_size)
- # 初始化MTP组件
- self.M = nn.ModuleList([
- nn.Linear(2*d_model, d_model, bias=False) for _ in range(num_layers)
- ])
- self.trm_blocks = nn.ModuleList([
- nn.TransformerEncoderLayer(d_model, n_head) for _ in range(num_layers)
- ])
- # 使用RMSNorm
- self.rms_norm = RMSNorm(d_model)
-
然后是前向传播函数的实现
- def forward(self, hidden_states, token_ids):
- """
- hidden_states: [T, B, D] 主模型输出
- token_ids: [T, B] 输入token IDs
- """
- T, B = token_ids.shape
- total_loss = 0.0
根据MTP结构图

与公式21
比如 将 t1的主模型表示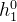 和 t2 的嵌入 Emb(t2)结合,通过公式 21 计算得到
和 t2 的嵌入 Emb(t2)结合,通过公式 21 计算得到
可得代码应该如下编写——实现的时候,要注意,将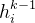 和
和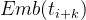 先各自进行RMSNorm后,再拼接
先各自进行RMSNorm后,再拼接- for k in range(1, self.D+1):
- # 步骤1:组合表示(公式21)
- prev_hidden = self.rms_norm(hidden_states) # h_i^{k-1}
- next_emb = self.shared_emb(token_ids[k:]) # Emb(t_{i+k})
- next_emb = self.rms_norm(next_emb)
- combined = torch.cat([prev_hidden[:-k], next_emb], dim=-1) # [T-k, B, 2D]
拼接之后,再做投影
projected = self.M[k-1](combined) # M_k投影 -
接着,做Transformer 处理:
将输入到 Transformer 块 TRM1 中,得到
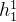
- # 步骤2:Transformer处理(公式22)
- trm_out = self.trm_blocks[k-1](
- projected.permute(1,0,2) # 转换为[B, T-k, D]
- ).permute(1,0,2) # 恢复[T-k, B, D]
-
最后,输出头预测:
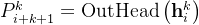
- # 步骤3:计算预测(公式23)
- logits = self.shared_out(trm_out) # [T-k, B, V]
-
损失计算
根据V3技术报告可知,对于每个预测深度,他们计算一个交叉熵损失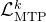 (如下公式24所示)
(如下公式24所示)![\mathcal{L}_{\mathrm{MTP}}^{k}=\operatorname{CrossEntropy}\left(P_{2+k: T+1}^{k}, t_{2+k: T+1}\right)=-\frac{1}{T} \sum_{i=2+k}^{T+1} \log P_{i}^{k}\left[t_{i}\right]](https://img1.iyenn.com/thumb02/c4a7c4f8a7c4b25d/356117394547807393774.jpeg%3D%5Coperatorname%7BCrossEntropy%7D%5Cleft%28P_%7B2+k%3A%20T+1%7D%5E%7Bk%7D%2C%20t_%7B2+k%3A%20T+1%7D%5Cright%29%3D-%5Cfrac%7B1%7D%7BT%7D%20%5Csum_%7Bi%3D2+k%7D%5E%7BT+1%7D%20%5Clog%20P_%7Bi%7D%5E%7Bk%7D%5Cleft%5Bt_%7Bi%7D%5Cright%5D)
其中T 表示输入序列长度,
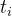 表示第
表示第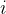 个位置的真实token,
个位置的真实token,![P_{i}^{k}\left[t_{i}\right]](https://img1.iyenn.com/thumb02/c4a7c4f8a7c4b25d/789617394547803557.jpeg) 表示由第k 个MTP 模块给出的
表示由第k 个MTP 模块给出的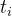 的相应预测概率
的相应预测概率
可得- # 计算损失(公式24)
- targets = token_ids[k+1:].reshape(-1) # 预测目标为i+k+1
- loss = nn.functional.cross_entropy(
- logits.view(-1, logits.size(-1)),
- targets,
- reduction='mean'
- )
- total_loss += loss
- 最后,他们计算所有深度上的MTP 损失的平均值,并将其乘以一个权重因子
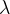 ,以获得总体MTP 损失
,以获得总体MTP 损失 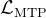 ,这作为DeepSeek-V3 的附加训练目标
,这作为DeepSeek-V3 的附加训练目标
相当于再做加权
- # 最终加权损失(公式25)
- return total_loss * (0.3 / self.D) # λ=0.3
3.2.2 完美融合:匹配V3官方代码库已有结构的MTP实现
根据DeepSeek-V3官方实现代码的架构风格,需要进行以下关键修改来实现无缝集成:
- 库的引入
- import torch
- import torch.nn as nn
- from deepseek_v3_modules import (
- DeepseekRMSNorm,
- MoETransformerLayer, # 使用项目中的MoE层代替标准Transformer
- RotaryEmbedding, # 使用项目自实现的RoPE
- FP8Linear # 使用项目中的FP8量化层
- )
- 初始化
- class MTPModule(nn.Module):
- def __init__(self, config):
- super().__init__()
- # 对齐项目参数命名规范
- self.depth = config.mtp_depth # 从config读取D值
- self.hidden_size = config.hidden_size
- # 使用项目自实现的组件 (与model.py保持一致)
- self.rms_norm = DeepseekRMSNorm(self.hidden_size, eps=config.rms_norm_eps)
- self.rope = RotaryEmbedding(dim=self.hidden_size // config.num_attention_heads)
- # 与主模型共享参数——即共享嵌入、共享输出头 (参考model.py的Embedding实现)
- self.shared_emb = None # 将在外部绑定
- self.shared_out = None
- # 使用项目中的MoE层 (替换原始Transformer层)
- self.mtp_layers = nn.ModuleList([
- MoETransformerLayer(
- config,
- layer_idx=layer_idx,
- is_mtp=True # 添加特殊标记
- ) for layer_idx in range(self.depth)
- ])
- # 使用项目中的FP8线性层
- self.proj_layers = nn.ModuleList([
- FP8Linear(
- 2 * self.hidden_size,
- self.hidden_size,
- fp8_params=config.fp8_params
- ) for _ in range(self.depth)
- ])
- 对于前向传播而言
- def forward(self, hidden_states, input_ids):
- """
- 对齐项目输入输出格式:
- hidden_states: [batch_size, seq_len, hidden_size]
- input_ids: [batch_size, seq_len]
- """
- batch_size, seq_len = input_ids.shape
- total_loss = 0.0
- for k in range(1, self.depth + 1):
- # 1. 组合表示 (适配项目维度格式)
- prev_hidden = self.rms_norm(hidden_states[:, :-k, :]) # [B, T-k, D]
- next_emb = self.shared_emb(input_ids[:, k:]) # [B, T-k, D]
- next_emb = self.rms_norm(next_emb)
- # 2. 应用RoPE (与model.py中的处理一致)
- prev_hidden = self.rope(prev_hidden)
- next_emb = self.rope(next_emb)
- # 3. 先拼接,后线性投影
- combined = torch.cat([prev_hidden, next_emb], dim=-1) # [B, T-k, 2D]
- projected = self.proj_layers[k-1](combined)
- # 4. 使用MoE层 (对齐项目实现)
- trm_out = self.mtp_layers[k-1](
- projected,
- attention_mask=None, # 假设因果掩码在外部处理
- position_ids=None # 与model.py中处理一致
- )[0]
- # 5. 计算损失
- logits = self.shared_out(trm_out) # [B, T-k, V]
- targets = input_ids[:, k+1:].reshape(-1)
- loss = nn.functional.cross_entropy(
- logits.view(-1, logits.size(-1)),
- targets,
- reduction='mean'
- )
- total_loss += loss
- # 动态lambda处理 (匹配4.3节训练策略)
- lambda_weight = 0.3 if self.training else 0.0
- return total_loss * (lambda_weight / self.depth)
至于如何与V3官方代码库中的推理文件model.py搭配,以及如何验证是否正确(上面的实现还是有些小问题的),暂见 《DeepSeek原理与项目实战营》中,本文后续再考虑是否更新
最后我说一下,虽然AI在上述的实现中只占了30%,但确实帮我省心了,可能有的同学好奇这个AI到底是哪个模型,嗯,非常非常的不难猜到:没错,过程中我主要就用的R1——通过Google账号登录
// 待更


![\mathbf{h}_{i}^{\prime k}=M_{k}\left[\operatorname{RMSNorm}\left(\mathbf{h}_{i}^{k-1}\right) ; \operatorname{RMSNorm}\left(\operatorname{Emb}\left(t_{i+k}\right)\right)\right]](https://img1.iyenn.com/thumb02/c4a7c4f8a7c4b25d/473917394547767391939.jpeg_%7Bi%7D%5E%7B%5Cprime%20k%7D%3DM_%7Bk%7D%5Cleft%5B%5Coperatorname%7BRMSNorm%7D%5Cleft%28%5Cmathbf%7Bh%7D_%7Bi%7D%5E%7Bk-1%7D%5Cright%29%20%3B%20%5Coperatorname%7BRMSNorm%7D%5Cleft%28%5Coperatorname%7BEmb%7D%5Cleft%28t_%7Bi+k%7D%5Cright%29%5Cright%29%5Cright%5D)
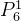
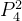
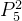
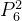
评论记录:
回复评论: