写在前面的话
k-means 算法是一个聚类的算法 也就是clustering 算法。是属于无监督学习算法,也是就样本没有label(标签)的算分,然后根据某种规则进行“分割”, 把相同的或者相近的objects 物体放在一起。
在这里K就是我们想要分割的的聚类的个数。
当然了,很多资料都会说这个算法吧,毕竟简单粗暴可依赖
算法描述
首先我们有以下的几个点
| A1 | (2,10) |
| A2 | (2,5) |
| A3 | (8,4) |
| A4 | (5,8) |
| A5 | (7,5) |
| A6 | (6,4) |
| A7 | (1,2) |
| A8 | (4,9) |
这个算法不能帮助我们自动分类,所以我们需要指定我们需要的个数。其实在很多实际应用当中,我们很难知道我们的数据是什么分布的,应该分成几类比较好。这也是k-means自身的一个缺陷,所以不能帮助我们自动的聚类。
注:如果我在本文中说了分类,其实是分割的意思,我想表达的意思是聚类。
中文和英文切换,在意思上表达真的有点差距。
现在假设我们需要把上面的数据点分成三类。我们需要遵循下面的几个步骤
- 选取三个类的初始中心
- 计算剩余点到这三个中心的距离
- 将距离中心点距离最短的点归为一类
- 依次划分好所有的数据点
- 重新计算中心
- 重复2-5 个步骤,直到中心点不会在变化为止
现在看完步骤,其实可能会有一些疑问:
1. 怎么选择我们的初始中心点?
2. 怎么计算点之间的距离呢。
选择中心点
中心点怎么选择,一般情况下我们是随机的从我们的数据集中选择的。当然还会有其他的方法,我们在之后的文章中可能会讨论。如果我还有时间去写的话,一般我会有时间写的。
甚至这个中心点的选择可以是完全随机的,甚至都不需要从我们的数据集中选取,在这里,我们的数据集是一个二维的,所以我们可以选择在XY坐标上的任意三个点,随你高兴都是可以的
注意:中心点的选取不同,最后的聚类结果可能大不相同
在这里我们假设我们的三个初始点是A,
在这里我们选取的初始点是A1,A4,A7
在这里我们定义两个点之间的距离用曼哈顿聚类距离,也可以叫做城市街区距离。
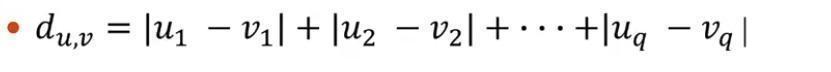
在这里我们是二维坐标,所以我们可以按照下面这个公式:
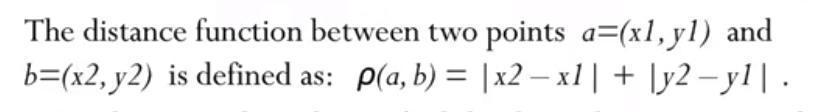
下面是一个例子:

计算的一般过程:
我们先看第一轮:
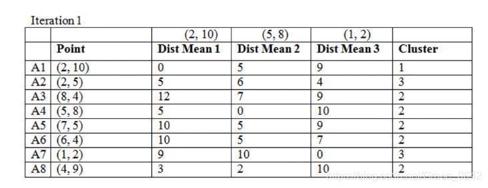
选取距离最近的归为一类
这个时候我们得到的聚类的结果:

得到了第一轮的结果我们需要重新的计算每个聚类的中心
cluster1
对于第一个聚类只有一个点所以它的聚类的中心就是它自己。
Cluster2
X:
(8+5+7+6+4)/5 = 6
Y:
(4+8+5+4+9)/5 = 6
这个时候它的中心就变成了(6,6)
Cluster3:
X:
(2+1)/2 = 1.5
Y:
(5+2)/2 = 3.5
这个时候在进行第二轮迭代:
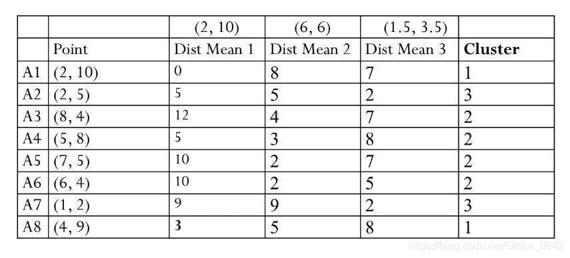
这个时候再次计算中心:

这个时候用我们的新的中心再来计算一遍:
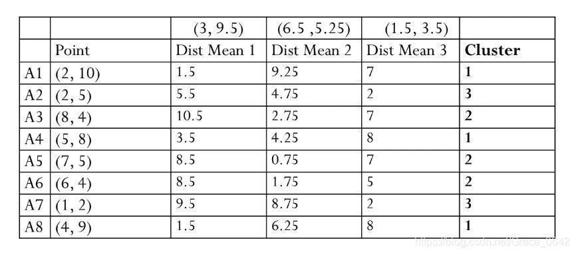
这个时候我们在重新根据新的聚类重新计算我们的中心:

得到新的点之后我们在重新计算新的聚类
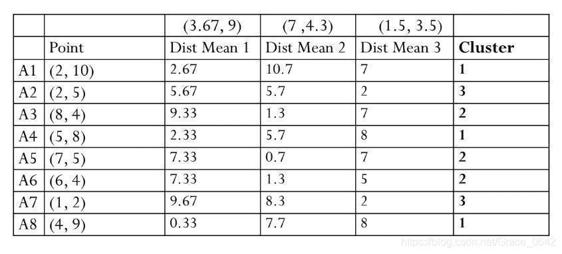
这个时候发现和上一次的结果是一致的,这个时候我们就可以停止我们的算法了。
下面我们来看一下这个迭代过程的图谱。
这个是我们的的初始过程
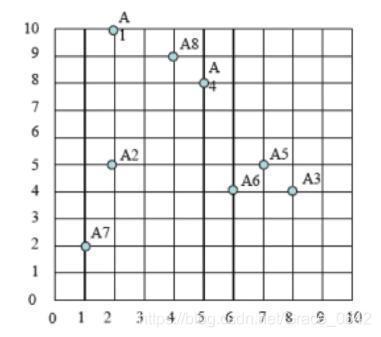
之后是我们选取中心点:
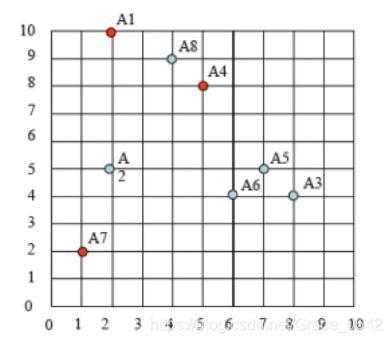
依次迭代的过程:
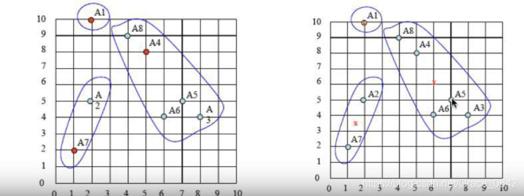
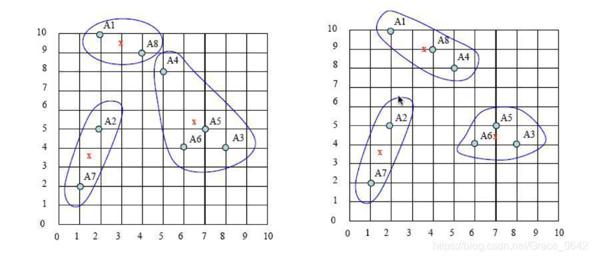
写在后面的话
无意中发现了一个巨牛的人工智能教程,忍不住分享一下给大家。教程不仅是零基础,通俗易懂,而且非常风趣幽默,像看小说一样!觉得太牛了,所以分享给大家。点这里可以跳转到教程 http://iyenn.com/index/link?url=https://www.cbedai.net/chichoxian
喜欢的,你懂的~
救救孩子吧


Reference:
http://iyenn.com/index/link?url=https://www.youtube.com/watch?v=_S5tvagaQRU

评论记录:
回复评论: