引言

从本节开始，介绍反向传播算法($\text{BackPropagation,BP}$)，本节将介绍$\text{M-P}$神经元模型与感知机算法的关系。

$\text{M-P}$神经元模型

本部分是针对前馈神经网络模型结构上的理论上的补充说明。详见《机器学习》(周志华著)P98。

$\text{M-P}$神经元模型由$\text{1943}$年被提出，它是神经网络的基本组成单位：

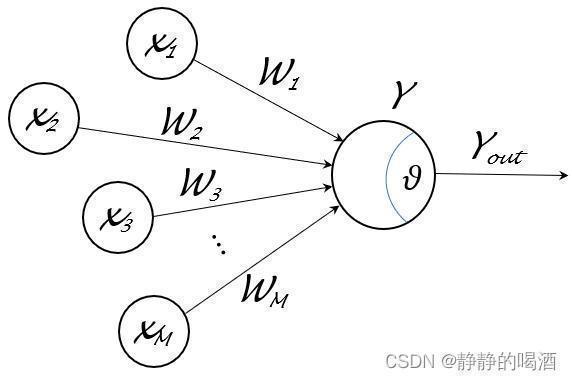
• 这里的$x_m(m=1,2,\cdots ,\mathcal{M})$表示$\mathcal{M}$个其他神经元，如果是输入层，那么$x_m$表示样本特征$\mathcal{X}$的随机变量集合；对应的${\mathcal{W}}_m(m=1,2,\cdots ,\mathcal{M})$表示各神经元向神经元$\mathcal{Y}$传递过程中对应的权重信息。
• $\theta$被称作阈值($\text{Threshold}$)。从逻辑意义的角度观察，它可以看作成一个触发器：一旦神经元$\mathcal{Y}$接收到的总输入值超过阈值$\theta$，那么神经元$\mathcal{Y}$就被激活，从而得到神经元$\mathcal{Y}$的输出结果$y_{out}$：
  但从数学意义的角度观察，总输入值${\sum }_{m=1}^{\mathcal{M}}{\mathcal{W}}_m{x}_m$与阈值$\theta$计算了它们之间的偏差${\sum }_{m=1}^{\mathcal{M}}{\mathcal{W}}_m{x}_m-\theta$。也就是说，神经元$\mathcal{Y}$总是会被激活的，只不过激活的效果视偏差结果而定。
  $$y_{out}=f\left(\sum _{m=1}^{\mathcal{M}}{\mathcal{W}}_m{x}_m-\theta \right)$$

其中$f(\cdot )$表示激活函数($\text{Activation Function}$)。上式表示的具体流程为：
需要注意的点：$x_m(m=1,2,\cdots ,\mathcal{M})$如果不是输出层的神经元，那么它们每个神经元也应存在对应的阈值，只不过上图没有将其画出而已。

• 神经元$\mathcal{Y}$将接收到其他$\mathcal{M}$个其他神经元$x$的输入信号，并通过这些输入信号通过带权重$\mathcal{W}$的连接($\text{Connection}$)向神经元$\mathcal{Y}$进行传递；
• 神经元$\mathcal{Y}$将接收到的总输入结果${\sum }_{m=1}^{\mathcal{M}}{\mathcal{W}}_m{x}_m$与神经元$\mathcal{Y}$的阈值$\theta$之间进行比较；
• 最终将比较结果${\sum }_{m=1}^{\mathcal{M}}{\mathcal{W}}_m{x}_m-\theta$通过激活函数处理以产生神经元$\mathcal{Y}$的输出$y_{out}$。

关于激活函数，理想状态下的激活函数就是指示函数自身：

• 当比较结果${\sum }_{m=1}^{\mathcal{M}}{\mathcal{W}}_m{x}_m-\theta >0$时，神经元$\mathcal{Y}$必然以状态$1$的情况下被激活;相反，如果总输入结果$<$阈值时，神经元$\mathcal{Y}$必然以和状态$1$相反的状态$0$情况下激活。
• 之所以称之为‘理想状态’，是因为该函数的功能与上面描述的完全一致，没有出现流程错误的可能性。
  

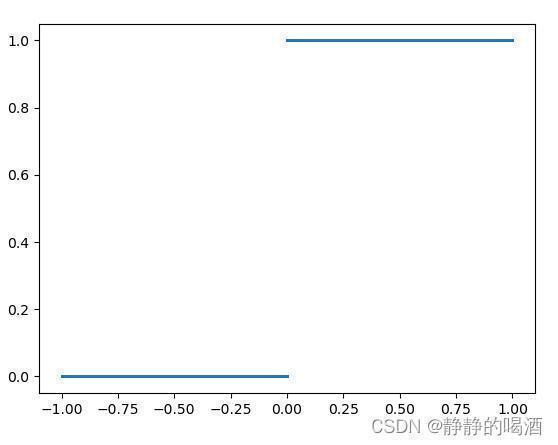
然而，指示函数自身并不是连续函数，着意味着该函数并非在其定义域内处处可导。如果针对损失函数求解连接权重${\mathcal{W}}_m(m=1,2,\cdots ,\mathcal{M})$的最优值，上述函数因无法求导而无法对权重信息进行更新，这并不是一个好的性质。

因此，实际上通常使用$\text{Sigmoid}$函数作为激活函数。$\text{Sigmoid}$函数图像表示如下：
关于$\text{Sigmoid}$函数，不仅在‘激活函数’中提到过，在逻辑回归($\text{Logistic Regression}$),以及受限玻尔兹曼机($\text{Restricted Boltzmann Machine,RBM}$)——后验概率求解中都提到过相关性质。后续会专门写一篇关于$\text{Sigmoid}$函数的总结。
标记-> 关键词:对数几率函数。

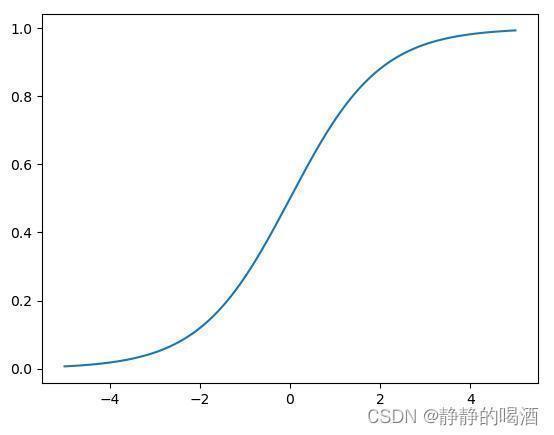
该函数的特点相比指示函数可在其定义域上处处连续、可导，这样在迭代求解连接权重时，能够对连接权重的最优方向进行计算；相反，依然从概率的角度观察，$\text{Sigmoid}$激活函数并没有指示函数那样准确和果断：

• 当总输入结果超过阈值时，我们仅是分配一个 稍微高一点($>0.5$)的神经元激活状态。
• 相反，当总输入结果小于阈值时，依然存在一定神经元激活状态，只不过和指示函数相比，它们的区别可能小很多。

由于$\text{Sigmoid}$函数能够把较大范围内变化的输入值压缩到$(0,1)$范围的区间内，因而也称$\text{Sigmoid}$函数为挤压函数$(\text{Squashing Function})$。

而神经网络($\text{Neural Network}$)就是这些神经元模型按照一定的层次结构连接起来得到的模型结果。
‘按照一定层次结构’本质上是若干个$y_j=f\left({\sum }_{m=1}^{\mathcal{M}}{\mathcal{W}}_m{x}_m-{\theta }_j\right)$的嵌套结果。

$\text{M-P}$神经元模型与感知机算法

感知机算法的参数学习

既然知道了$\text{M-P}$神经元模型对于任务的处理流程，下面通过感知机算法为例进行描述，它是如何实现这一过程的。

感知机算法($\text{Perceptron}$)由两层神经元构成：

• 输入层：接收外界信号并将其传递给输出层；
• 输出层：该层由一个$\text{M-P}$神经元组成，对输入层传递的信号进行计算，并根据计算结果对输入信号的性质进行判别。

感知机算法能够容易地实现与、或、非逻辑运算。关于$\text{M-P}$神经元模型的计算流程：$y=f\left({\sum }_{m=1}^{\mathcal{M}}{\mathcal{W}}_m{x}_m-\theta \right)$，假定激活函数$f(\cdot )$是指示函数，以逻辑与运算为例：

• 输入样本集合${\mathcal{D}}_{\text{AND}}$：
  $$\begin{array}{rl}{\mathcal{D}}_{\text{AND}}& ={\left\{\left[(x_1^{(i)},x_2^{(i)}),y^{(i)}\right]\right\}}_{i=1}^4\\ & =\{[(1,1),1],[(1,0),0],[(0,1),0],[(0,0),0]\}\end{array}$$
• 这里关于参数的学习过程暂时省略，先观察一个样本集合${\mathcal{D}}_{\text{AND}}$学习正确的模型结果：
  $$y=f\left(1\cdot x_1+1\cdot x_2-2\right)$$

可以发现，此时${\mathcal{D}}_{\text{AND}}$中任意一个样本均可以通过该模型划分正确。其中${\mathcal{W}}_1={\mathcal{W}}_2=1,\theta =2$。继续从$\text{M-P}$神经元模型的角度观察，激活函数$f(\cdot )$内的项可表示为如下形式：
而公式中的$\theta =x_3$被称作‘哑结点’$(\text{Dummy Node})$，其结果是某固定值，不发生变化。
$$\begin{array}{rl}1\cdot x_1+1\cdot x_2-2& \Rightarrow \underset{=1}{\underbrace{{\mathcal{W}}_1}}\cdot x_1+\underset{=1}{\underbrace{{\mathcal{W}}_2}}\cdot x_2+\underset{=2}{\underbrace{{\mathcal{W}}_3}}\cdot \underset{\theta ;\text{fixed;=-1}}{\underbrace{x_3}}\\ & \Rightarrow \sum _{m=1}^3{\mathcal{W}}_m\cdot x_m\end{array}$$
这种操作意味着：阈值$\theta$我们不必计较它的数值具体是多少，我们仅需要将${\mathcal{W}}_3$学习正确，阈值自然迎刃而解。也就是说，权重参数和阈值的学习过程可统一为权重参数的学习。

感知机算法的参数调整

感知机算法对于权重参数的调整表示如下：
该部分是关于《机器学习》(周志华著)P99页中式5.1,式5.2的推导过程。
由于感知机算法策略的构建动机是错误驱动，我们将真实数据集$\mathcal{D}=\{(x^{(i)},y^{(i)}){\}}_{i=1}^N$划分成两个部分：

• 被正确分类的样本集合：由于$f(\cdot )$是指示函数，在定义域内，其函数结果非负，并且$y^{(i)}$与预测结果${\mathcal{W}}^T{x}^{(i)}$之间同号。因而样本集合${\mathcal{D}}_{\text{True}}$表示为：
  $${\mathcal{D}}_{\text{True}}=\left\{(x^{(i)},y^{(i)})\mid y^{(i)}({\mathcal{W}}^T{x}^{(i)})\ge 0\right\}$$
• 同理，被错误分类的样本集合${\mathcal{D}}_{\text{False}}$：
  $${\mathcal{D}}_{\text{False}}=\left\{(x^{(i)},y^{(i)})\mid y^{(i)}({\mathcal{W}}^T{x}^{(i)})<0\right\}$$
• 并且有：
  $$\mathcal{D}={\mathcal{D}}_{\text{True}}\cup {\mathcal{D}}_{\text{False}}$$

分别观察两组集合：

• 首先观察分类正确的样本集合${\mathcal{D}}_{True}$：此时$y^{(i)}={\hat{y}}^{(i)}$，从权重学习的角度，我们希望集合${\mathcal{D}}_{\text{True}}$越接近$\mathcal{D}$越好，也就是说，在$\mathcal{D}$中，我们的${\hat{y}}^{(i)}\left({\mathcal{W}}^T{x}^{(i)}\right)$越大越好：
  如果${\hat{y}}^{(i)}\left({\mathcal{W}}^T{x}^{(i)}\right)$越大，越意味着‘有更多的样本被划分正确’，并将该逻辑应用在完整的数据集$\mathcal{D}$中。
  对应目标函数${\mathcal{L}}_{\text{True}}(\mathcal{W})$表示如下：
  需要注意的点：该损失函数是基于$y^{(i)}={\hat{y}}^{(i)}$条件下实现的，并且${\hat{y}}^{(i)}\left({\mathcal{W}}^T{x}^{(i)}\right)\ge 0$恒成立。因此一定求解的是最大值$\mathrm{argmax}$.
  $$\{\begin{array}{l}{\mathcal{L}}_{\text{True}}(\mathcal{W})={\sum }_{(x^{(i)},y^{(i)})\in \mathcal{D}}{\hat{y}}^{(i)}\left({\mathcal{W}}^T{x}^{(i)}\right)\\ \underset{\mathcal{W}}{\mathrm{argmax}}{\mathcal{L}}_{\text{True}}(\mathcal{W})\end{array}$$
  对损失函数${\mathcal{L}}_{\text{True}}(\mathcal{W})$求解偏导：
  $$\frac{\partial {\mathcal{L}}_{\text{True}}(\mathcal{W})}{\partial \mathcal{W}}={\nabla }_{\mathcal{W}}{\mathcal{L}}_{\text{True}}(\mathcal{W})=\sum _{(x^{(i)},y^{(i)})\in \mathcal{D}}{\hat{y}}^{(i)}{x}^{(i)}$$

• 同理，我们观察分类错误的样本集合${\mathcal{D}}_{\text{False}}$：由于${\mathcal{D}}_{\text{False}}$中$y^{(i)}$与预测结果${\mathcal{W}}^T{x}^{(i)}$之间异号，因此该集合中的样本$y^{(i)}\left({\mathcal{W}}^T{x}^{(i)}\right)\le 0$恒成立。从权重学习的角度观察，${\sum }_{x^{(i)},y^{(i)}\in {\mathcal{D}}_{\text{False}}}{y}^{(i)}\left({\mathcal{W}}^T{x}^{(i)}\right)$结果越大越好。

  因为在小于$0$的前提下，数值越大意味着错误分类的样本越少。并且我们希望将该逻辑应用在完整的数据集合$\mathcal{D}$中：
  对应的目标函数${\mathcal{L}}_{\text{False}}(\mathcal{W})$表示如下：

  • 需要注意的点：该损失函数是基于${\hat{y}}^{(i)},y^{(i)}$之间异号的条件下成立的，因而$y^{(i)}\left({\mathcal{W}}^T{x}^{(i)}\right)<0$恒成立。为了和${\mathcal{L}}_{\text{True}}(\mathcal{W})$同号，应将$\underset{\mathcal{W}}{\mathrm{argmax}}{\mathcal{L}}_{\text{False}}(\mathcal{W})$转化为相应的$\underset{\mathcal{W}}{\mathrm{argmin}}$形式。
  • 这里转化的核心原因：如果不转化，损失函数${\mathcal{L}}_{\text{False}}(\mathcal{W})$没有下界；相反，如果转化了，${\mathcal{L}}_{\text{True}}(\mathcal{W}),{\mathcal{L}}_{\text{False}}(\mathcal{W})$均恒正，并且均存在下界为$0$,这两个损失函数才能相加。
    $$\{\begin{array}{l}{\mathcal{L}}_{\text{False}}(\mathcal{W})={\sum }_{(x^{(i)},y^{(i)})\in \mathcal{D}}{y}^{(i)}\left({\mathcal{W}}^T{x}^{(i)}\right)\\ \underset{\mathcal{W}}{\mathrm{argmax}}{\mathcal{L}}_{\text{False}}(\mathcal{W})\end{array}\Rightarrow \{\begin{array}{l}{\mathcal{L}}_{\text{False}}(\mathcal{W})=-{\sum }_{(x^{(i)},y^{(i)})\in \mathcal{D}}{y}^{(i)}\left({\mathcal{W}}^T{x}^{(i)}\right)\\ \underset{\mathcal{W}}{\mathrm{argmin}}{\mathcal{L}}_{\text{False}}(\mathcal{W})\end{array}$$

  对损失函数${\mathcal{L}}_{\text{False}}(\mathcal{W})$求解偏导：
  $$\frac{\partial {\mathcal{L}}_{\text{False}}(\mathcal{W})}{\partial \mathcal{W}}={\nabla }_{\mathcal{W}}{\mathcal{L}}_{\text{False}}(\mathcal{W})=\sum _{(x^{(i)},y^{(i)})\in \mathcal{D}}-y^{(i)}{x}^{(i)}$$

至此，关于两个损失函数${\mathcal{L}}_{\text{True}}(\mathcal{W}),{\mathcal{L}}_{\text{False}}(\mathcal{W})$均恒正，并且下界均为$0$，将两损失函数的梯度相加，有：
$$\begin{array}{rl}{\nabla }_{\mathcal{W}}\mathcal{L}(\mathcal{W})& =\frac{\partial \mathcal{L}(\mathcal{W})}{\partial \mathcal{W}}\\ & =\frac{\partial {\mathcal{L}}_{\text{False}}(\mathcal{W})}{\partial \mathcal{W}}+\frac{\partial {\mathcal{L}}_{\text{True}}(\mathcal{W})}{\partial \mathcal{W}}\\ & =\sum _{(x^{(i)},y^{(i)})\in \mathcal{D}}\left({\hat{y}}^{(i)}-y^{(i)}\right)x^{(i)}\end{array}$$
最终，使用梯度下降法对模型参数进行迭代：
$$\begin{array}{rl}{\mathcal{W}}^{(t+1)}& \Leftarrow {\mathcal{W}}^{(t)}-\eta \cdot {\nabla }_{\mathcal{W}}\mathcal{L}(\mathcal{W})\\ & ={\mathcal{W}}^{(t)}+\eta \sum _{(x^{(i)},y^{(i)})\in \mathcal{D}}\left(y^{(i)}-{\hat{y}}^{(i)}\right)x^{(i)}\end{array}$$
观察这个关于$\mathcal{W}$的迭代公式，如果感知机对样本$(x^{(i)},y^{(i)})$预测正确，即${\hat{y}}^{(i)}=y^{(i)}$，这意味着${\mathcal{W}}^{(t+1)}={\mathcal{W}}^{(t)}$，感知机模型的参数已经学习完成；否则继续根据误差的梯度对参数$\mathcal{W}$进行调整。

下一节将介绍反向传播算法($\text{BackPropagation}$)。

相关参考：
机器学习(周志华著)