前言

读TensorFlow相关代码看到了STN的应用，搜索以后发现可替代池化，增强网络对图像变换(旋转、缩放、偏移等)的抗干扰能力，简单说就是提高卷积神经网络的空间不变性。

国际惯例，参考博客：

理解Spatial Transformer Networks

github-STN

Deep Learning Paper Implementations: Spatial Transformer Networks - Part I

Deep Learning Paper Implementations: Spatial Transformer Networks - Part II
将STN加入网络训练的一个关于图像隐写术的案例:StegaStamp

理论

图像变换

因为图像的本质就是矩阵，那么图像变换就是矩阵变换，先复习一下与图像相关的矩阵变换。假设$M$为变换矩阵，$N$为图像，为了简化表达，设$M$的维度是$(2,2)$，$N$代表像素点坐标，则维度是$(2,1)$，以下操作均为对像素位置的调整操作，而非对像素值的操作。

• 缩放
  M × N = [ p 0 0 q ] × [ x y ] = [ p x q y ] M imes N=

  $$egin{bmatrix} p&0\ 0&q end{bmatrix}$$ imes $$egin{bmatrix} x\y end{bmatrix}$$ = $$egin{bmatrix} px\qy end{bmatrix}$$ M×N=[p0​0q​]×[xy​]=[pxqy​]

• 旋转：绕原点顺时针旋转$\theta$角
  M × N = [ cos ⁡ θ − sin ⁡ θ sin ⁡ θ cos ⁡ θ ] × [ x y ] = [ x cos ⁡ θ − y sin ⁡ θ x sin ⁡ θ + y cos ⁡ θ ] M imes N=

  $$egin{bmatrix} cos heta&-sin heta\ sin heta&cos heta end{bmatrix}$$ imes $$egin{bmatrix} x\y end{bmatrix}$$ = $$egin{bmatrix} xcos heta-ysin heta\xsin heta+ycos heta end{bmatrix}$$ M×N=[cosθsinθ​−sinθcosθ​]×[xy​]=[xcosθ−ysinθxsinθ+ycosθ​]

• 错切(shear)：类似于将字的正体变成斜体
  M × N = [ 1 m n 1 ] × [ x y ] = [ x + m y y + n x ] M imes N=

  $$egin{bmatrix} 1&m\ n&1 end{bmatrix}$$ imes $$egin{bmatrix} x\y end{bmatrix}$$ = $$egin{bmatrix} x+my\y+nx end{bmatrix}$$ M×N=[1n​m1​]×[xy​]=[x+myy+nx​]

• 平移：要转换为齐次矩阵做平移
  M ′ × N ′ = [ 1 0 a 0 1 b ] × [ x y 1 ] = [ x + a y + b ] M' imes N'=

  $$egin{bmatrix} 1&0&a\ 0&1&b end{bmatrix}$$ imes $$egin{bmatrix} x\y\1 end{bmatrix}$$ = $$egin{bmatrix} x+a\y+b end{bmatrix}$$ M′×N′=[10​01​ab​]×⎣⎡​xy1​⎦⎤​=[x+ay+b​]

盗用参考博客的图解就是：

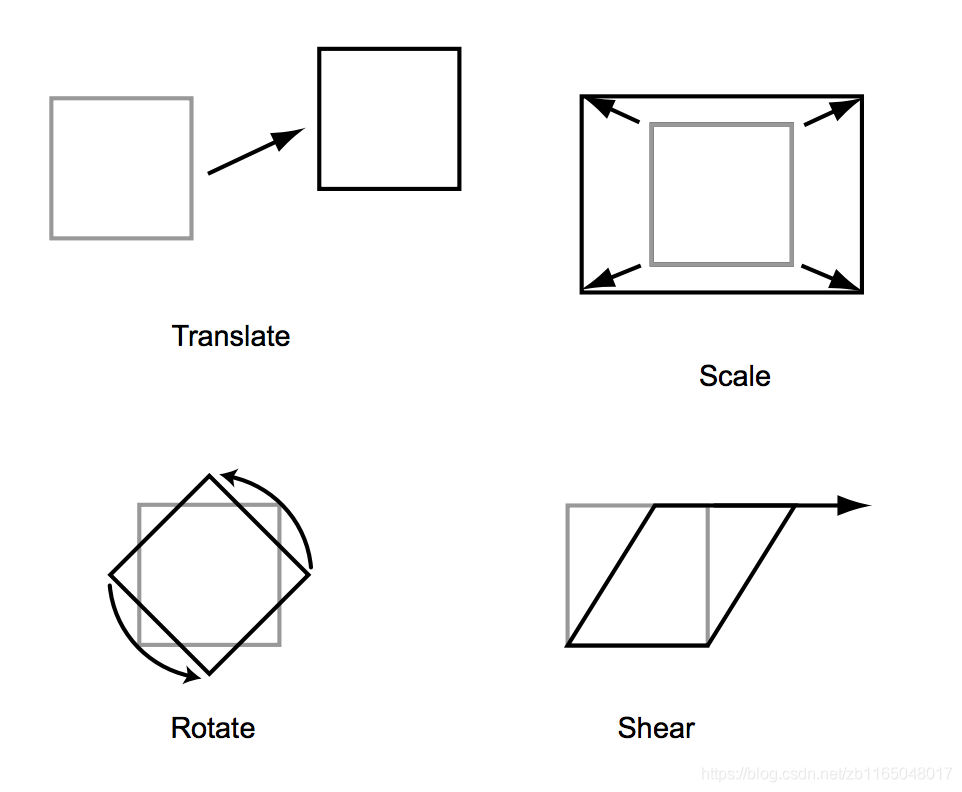
注意，我们进行多次变换的时候有多个变换矩阵，如果每次计算一个变换会比较耗时，参考矩阵的乘法特性，我们可以先将变换矩阵相乘，得到一个完整的矩阵代表所有变换，最后乘以图像，就可将图像按照组合变换顺序得到变换图像。这个代表一系列的变换的矩阵通常表示为:
M = [ a b c d e f ] M=

$$egin{bmatrix} a&b&c\d&e&f end{bmatrix}$$ M=[ad​be​cf​]
因为直接计算位置的值，很可能得到小数，比如将$(3,3)$的图像放大到$(9,9)$，也就是放大3倍，那么新图像$(8,8)$位置的像素就是原图$(8/3,8/3)$位置的像素，但是像素位置不可能是小数，因而出现了解决方案：双线性插值

双线性插值

先复习一下线性插值，直接去看之前写的这篇博客，知道$(x_1,y_1)$与$(x_2,y_2)$，求$(x_1,x_2)区间内的点$$x$位置的y值，结果是：
$$y=\frac{x-x_2}{x_1-x_2}{y}_1+\frac{x-x_1}{x_2-x_1}{y}_2$$
可以发现线性插值是针对一维坐标的，即给$x$求$y$，但是双线性插值是针对二维坐标点的，即给$(x,y)$求值$Q$。方法是先在$x$轴方向做两次线性插值，再在$y$轴上做一次线性插值。

设需要求$(x,y)$处的值，我们需要预先知道其附近四个坐标点及其对应的值，如:

• $(x,y)$左下角坐标为$(x_1,y_1)$，值为$Q_1$
• $(x,y)$右下角坐标为$(x_2,y_1)$， 值为$Q_2$
• $(x,y)$左上角坐标为$(x_1,y_2)$， 值为$Q_3$
• $(x,y)$右上角坐标为$(x_2,y_2)$，值为$Q_4$

首先对下面的$(x_1,y_1)$和$(x_2,y_1)$做线性插值，方法是把它两看做一维坐标$(x_1,Q_1)$和$(x_2,Q2)$，得到：
$$P_1=\frac{x-x_2}{x_1-x_2}{Q}_1+\frac{x-x_1}{x_2-x_1}{Q}_2$$
同理得到上面的两个坐标$(x_1,y_2)$与$(x_2,y_2)$的插值结果，也就是$(x_1,Q_3)$和$(x_2,Q_4)$的线性插值结果:
$$P_2=\frac{x-x_2}{x_1-x_2}{Q}_3+\frac{x-x_1}{x_2-x_1}{Q}_4$$
再对$(y_1,P_1)$和$(y_2,P_2)$做线性插值：
$$P=\frac{x-y_2}{y_1-y_2}{P}_1+\frac{y-y_1}{y_2-y_1}{P}_2$$
解决上面图像变换的问题，假设变换后的坐标不是整数，那么就选择这个坐标四个角的坐标的双线性插值的结果，比如$(8/3,8/3)$位置的像素就是$(2,2),(3,2),(2,3),(3,3)$位置像素的双线性插值结果。

总之就是先计算目标图像像素在源图像中的位置，然后得到源图像位置是小数，针对小数位置的四个顶点做双线性插值。

上面就是STN做的工作，也可以发现STN接受的参数就是6个，接下来看看为什么STN能提高卷积网络的旋转、平移、缩放不变性。

总结一下：

图像处理中的仿射变换通常包含三个步骤：

• 创建由$(x,y)$组成的采样网格，比如$(400,400)$的灰度图对应创建一个同样大小的网格。
• 将变换矩阵应用到采样网格上
• 使用插值技术从原图中计算变换图的像素值

池化

强行翻译一波这篇文章关于池化的部分，建议看原文，这里摘取个人认为重要部分：

池化在某种程度上增加了模型的空间不变性，因为池化是一种下采样技术，减少了每层特征图的空间大小，极大减少了参数数量，提高了运算速度。

池化提供的不变性确切来说是什么？池化的思路是将一个图像切分成多个单元，这些复杂单元被池化以后得到了可以描述输出的简单的单元。比如有3张不同方向的数字7的图像，池化是通过图像上的小网格来检测7，不受7的位置影响，因为通过聚集的像素值，我们得到的信息大致一样。个人觉得，作者的本意是单看小网格，是有很多一样的块。

池化的缺点在于：

• 丢失了75%的信息(应该是$(2,2)$的最大值池化方法)，意味着我们一定丢了是精确的位置信息。有人会问，这样可以增加空间鲁棒性哇。然而，对于视觉识别人物，空间信息是非常重要的。比如分类猫的时候，知道猫的胡须的位置相对于鼻子的位置有可能很重要，但是如果使用最大池化，可能丢失了这个信息。
• 池化是局部的且预定义好的。一个小的接受域，池化操作的影响仅仅是针对更深的网络层(越深感受野越大)，也就是中间的特征图可能受到严重的输入失真的影响。我们不能任意增加接受域，这样会过度下采样。

主要结论就是卷积网络对于相对大的输入失真不具有不变性。

The pooling operation used in convolutional neural networks is a big mistake and the fact that it works so well is a disaster. (Geoffrey Hinton, Reddit AMA)
1

STN理论

STN的全称是Spatial Transformer Networks，空间变换网络。时空变换机制就是通过给CNN提供显式的空间变换能力，以解决上述池化出现的问题。有三种特性：

• Modular：STN能够被插入到网络的任意地方，仅需很小的调整
• differentiable：STN可以通过反向传播训练
• dynamic：STN是对每个输入样本的一个特征图做空间变换，而池化是针对所有样本。

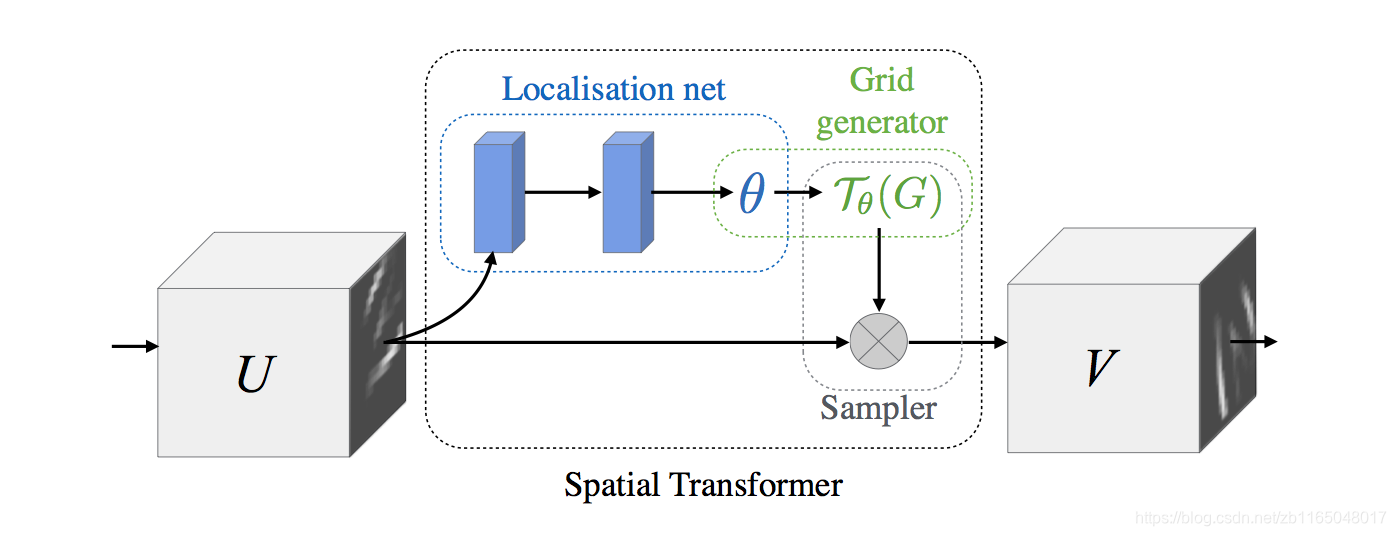
上图是STN网络的主要框架。所以到底什么是空间变换？通过结构图可发现模型包含三部分：localisation network、grid generator、sampler。

Localisation Network

主要是提取被应用到输入特征图上的仿射变换的参数$\theta$，网络结构是：

• 输入：大小为$(H,W,C)$的特征图$U$
• 输出：大小为$(6,1)$的变换矩阵$\theta$
• 结构：全连接或者卷积

Parametrised Sampling Grid

输出参数化的采样网格，是一系列的点，每个输入特征图能够产生期望的变换输出。

具体就是：网格生成器首先产生于输入图像$U$大小相同的标准网格，然后将仿射变换应用到网格。公式表达即，假设输入图的索引是$(x^t,y^t)$，将$\theta$代表的变换应用到坐标上得到新的坐标：
[ x s y s ] = [ θ 1 θ 2 θ 3 θ 4 θ 5 θ 6 ] × [ x t y t 1 ]

$$egin{bmatrix} x^s\y^s end{bmatrix}$$ = $$egin{bmatrix} heta_1& heta_2& heta_3\ heta_4& heta_5& heta_6 end{bmatrix}$$ imes $$egin{bmatrix} x^t\y^t\1 end{bmatrix}$$ [xsys​]=[θ1​θ4​​θ2​θ5​​θ3​θ6​​]×⎣⎡​xtyt1​⎦⎤​
Differentiable Image Sampling

依据输入特征图和参数化采样网格，我们可以利用双线性插值方法获得输出特征图。注意，这一步我们可以通过制定采样网格的大小执行上采样或者下采样，很像池化。

左图使用了单位变换，右图使用了旋转的仿射变换。

【注】因为双线性插值是可微的，所以STN可以作为训练网络的一部分。

代码

利用STN前向过程做图像变换

GitHub上有作者提供了源码，也可以用pip直接安装。

代码直接贴了，稍微改了一点点：

导入包

import tensorflow as tf
import cv2
import numpy as np

from stn import spatial_transformer_network as transformer
1
2
3
4
5

读入图像，转换为四维矩阵：

img=cv2.imread('test_img.jpg')
img=np.array(img)
H,W,C=img.shape
img=img[np.newaxis,:]
print(img.shape)
1
2
3
4
5

旋转变换的角度

degree=np.deg2rad(45)
theta=np.array([
    [np.cos(degree),-np.sin(degree),0],
    [np.sin(degree),np.cos(degree),0]
])
1
2
3
4
5

构建网络结构

x=tf.placeholder(tf.float32,shape=[None,H,W,C])
with tf.variable_scope('spatial_transformer'):
    theta=theta.astype('float32')
    theta=theta.flatten()
    
    loc_in=H*W*C #输入维度
    loc_out=6 #输出维度
    W_loc=tf.Variable(tf.zeros([loc_in,loc_out]),name='W_loc')
    b_loc=tf.Variable(initial_value=theta,name='b_loc')
    
    #运算
    fc_loc=tf.matmul(tf.zeros([1,loc_in]),W_loc)+b_loc
    h_trans=transformer(x,fc_loc)
1
2
3
4
5
6
7
8
9
10
11
12
13

把图像喂进去，并显示图像

init=tf.global_variables_initializer()
with tf.Session() as sess:
    sess.run(init)
    y=sess.run(h_trans,feed_dict={x:img})
    print(y.shape)
    
y=np.squeeze(np.array(y,dtype=np.uint8))
print(y.shape)
cv2.imshow('trasformedimg',y)
cv2.waitKey()
cv2.destroyAllWindows()
1
2
3
4
5
6
7
8
9
10
11

重点关注网络构建：

权重w_loc是全零的大小为$(HWC,6)$的矩阵，偏置b_loc是大小为$(1,6)$的向量，这样经过运算

fc_loc=tf.matmul(tf.zeros([1,loc_in]),W_loc)+b_loc
1

得到的其实就是我们指定的旋转角度对应的6维变换参数，最后利用变换函数transformer执行此变换就行了。

将STN加入网络中训练

主要参考StegaStamp作者的写法，这里做STN部分加入网络的方法：
输入一张图片到如下网络结构(Keras网络结构搭建语法)：

stn_params = Sequential([
            Conv2D(32, (3, 3), strides=2, activation='relu', padding='same'),
            Conv2D(64, (3, 3), strides=2, activation='relu', padding='same'),
            Conv2D(128, (3, 3), strides=2, activation='relu', padding='same'),
            Flatten(),
            Dense(128, activation='relu')
        ])
1
2
3
4
5
6
7

得到$(1,128)$维的向量，其实用一个网络替换上面前向计算中的loc_in，目的是为了得到二维图像对应的一维信息
后面的过程就和前向计算一样了，定义权重和偏置：

W_fc1 = tf.Variable(tf.zeros([128, 6]), name='W_fc1')
b_fc1 = tf.Variable(initial_value=initial, name='b_fc1')
1
2

然后利用一维信息得到图像变换所需的6个值：

x = tf.matmul(stn_params, self.W_fc1) + self.b_fc1
1

最后利用STN库将变换应用到图像中，得到下一层网络结构的输入

transformed_image = stn_transformer(image, x, [self.height, self.width, 3])
1

可以看出，STN加入到网络后，训练参数有：

• 二维图像到一维特征向量的卷积+全连接网络的权重和偏置
• 一维向量到6维变换参数的权重和偏置

总结

通篇就是对池化方案的改变，使用STN能够增加网络的变换不变性，比池化的效果更好。

代码：

链接：https://pan.baidu.com/s/1kDs9T-Mf1F_mzQyvslcROA
提取码：crdu