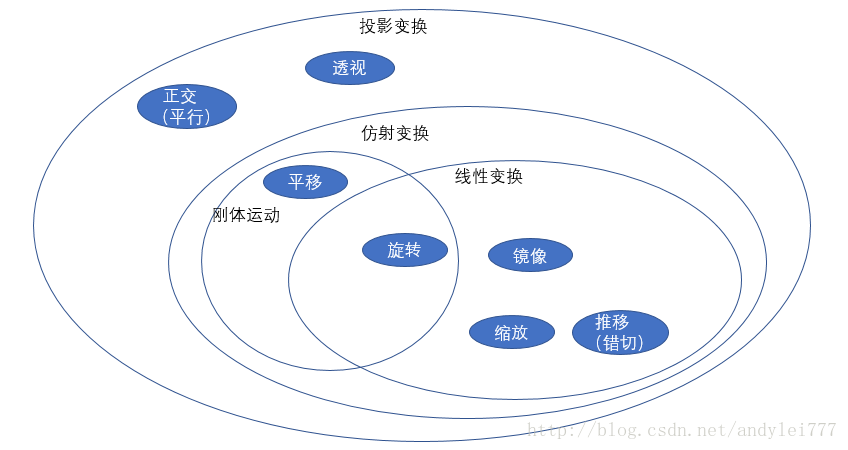
平面变换包括 线性变换，仿射变换等，
线性变换包括 旋转，镜像(翻转)，伸缩（缩放），推移（错切）
仿射变换 = 线性变换 + 平移

线性变换

直观定义：

• 变换前是直线变换后仍是直线（平行关系）
• 直线比例保持不变（比例关系）
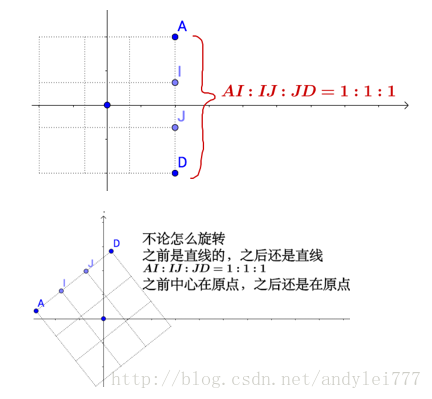
• 变换前是原点的，变换后依然是原点

几种基本线性变换（与对应的矩阵表示）：

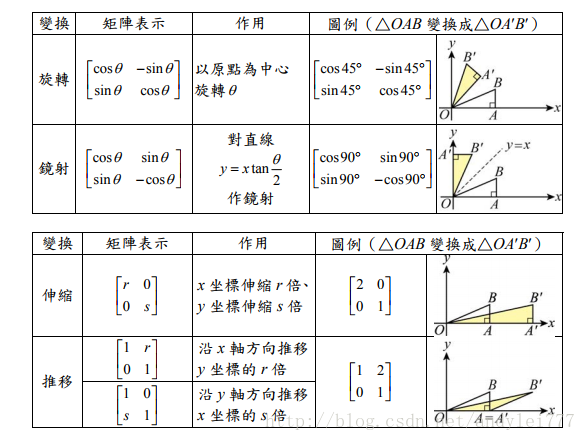
旋转

中学数学解释(几何角度)

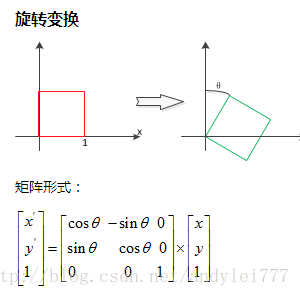
矩阵表示
一般的线性变换可由2x2的矩阵$A_{2x2}$表示，此处

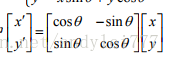
但是一般使用齐次矩阵表示（为了统一性，将平移时用到的加法也融入矩阵参数中）

大学数学解释（线性代数角度）
旋转操作可以看作由$R^2$映射到$R^2$,且可以验证它是线性变换。

数学表示为$T: R^2 xrightarrow[]{linear} R^2$

而任何线性变换都可以由对应的矩阵表示：$[T(v)]_{gamma} = [T]_{eta}^{gamma}[v]_{eta}$ （原向量空间的基底取$eta$，映射后的向量空间基地为$gamma$）

取定好${eta},{gamma}$ 之后很容易将 $[T]_{eta}^{gamma}$表示出来

翻转（镜像）

中学数学推导(几何角度)

大学数学解释（线性代数角度）

镜像是$R^2$空间上的线性变换（可以验证），在原始空间中找镜像点不是很方便，可以通过坐标变换的手法，将镜像变换转移到镜像直线为轴的坐标系来来求解。提示$T = ITI$。

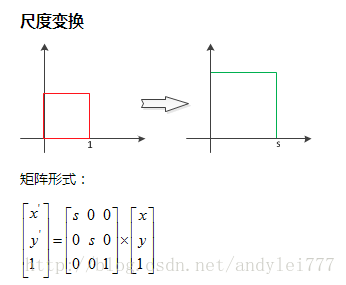
缩放（伸缩）

推移（错切？）

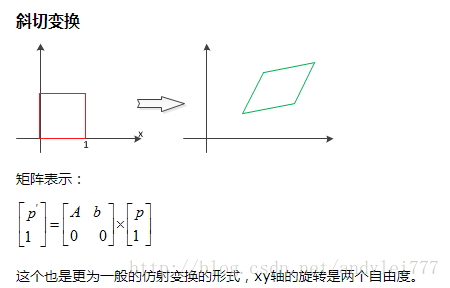
小结：

仿射变换

特点：

• 平行关系不变
• 比例关系不变

包括： 平移 + 旋转 镜像 缩放 推移

平移的矩阵表示：

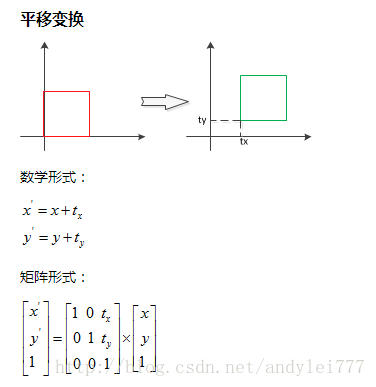
通用的矩阵表示：

由于仿射变换包含平移，所以需要表达相加。可以用齐次矩阵将加法用矩阵表示出来（也可以认为三维的线性变换可以表达二维的放射变换：三维的推移变换 可以表达二维的平移变换）。

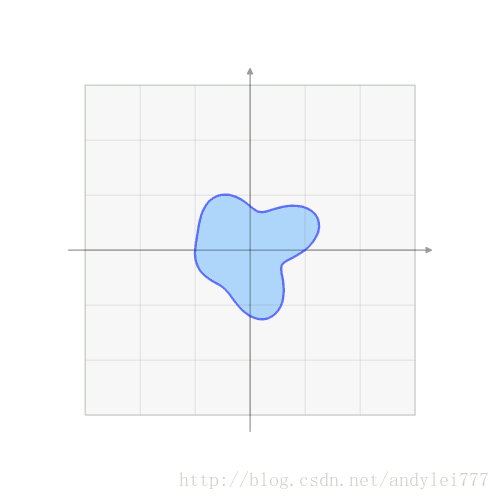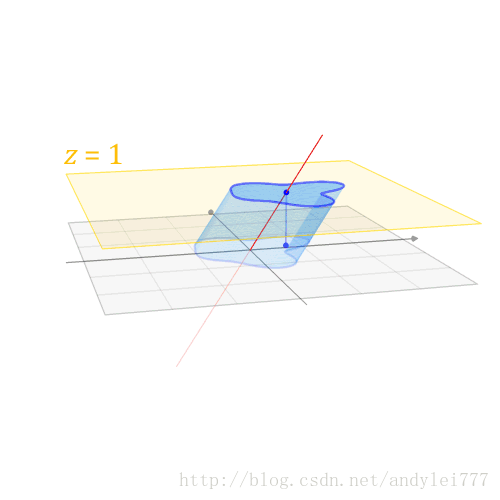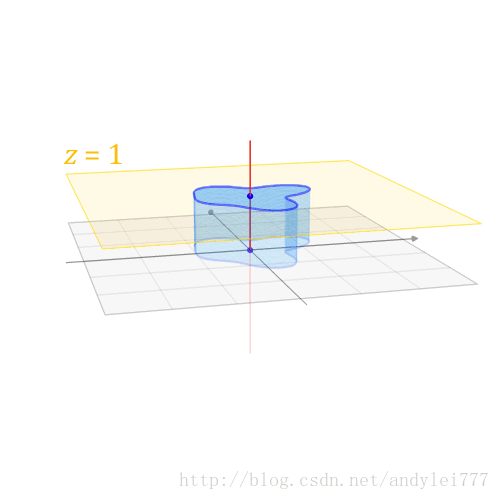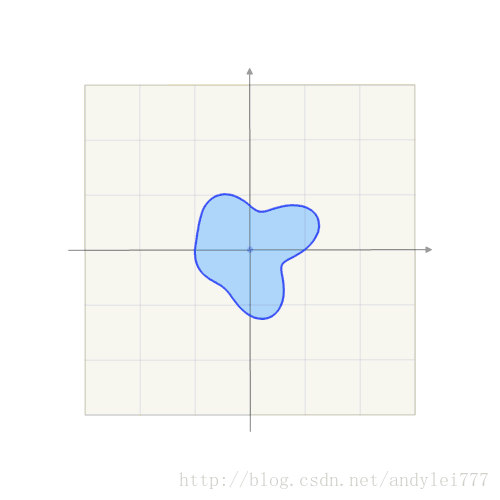
投影变换：

总结

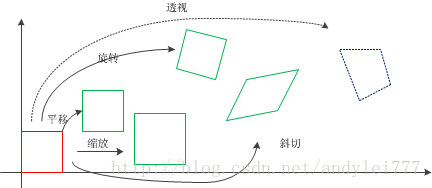
ps:

【参考】：
- 99課綱教學重點整理4-3-4矩陣-二階方陣表示的線性變換.pdf
- http://www.matongxue.com/madocs/244.html#/madoc
- http://iyenn.com/index/link?url=http://www.cnblogs.com/houkai/p/6660272.html
- http://iyenn.com/index/link?url=https://homepages.inf.ed.ac.uk/rbf/HIPR2/affine.htm GeometricTransformations
- http://iyenn.com/index/link?url=http://nghiaho.com/?p=2208 opencv