☞ ░ 前往老猿Python博文目录 https://blog.csdn.net/LaoYuanPython ░

一、引言

本系列文章记录老猿自学冈萨雷斯《数字图像处理》的感悟和总结，不过估计更新会比较慢，白天要工作，都是晚上抽空学习，学习完一章再回头总结，想学的朋友可以自己下载英文原版（目前到第四版）和中文译本（目前应该到第三版）的电子版观看，如果想对照观看建议英文原版也找第三版。

这本《数字图像处理》不愧为数字图像处理的经典教程，知识范围广、内容详尽、案例贴近实践，至少很合老猿的口味。但中译本存在两个问题：

1. 有些翻译得不够精准或流利，对于这样的内容如果在老猿总结知识中出现，会以斜体字标记，有些关键术语老猿会附上英文原词；
2. 中译本的图像案例很多都比原版差很多，甚至差到影响对讲述内容的理解，因此就算不看原版文字，图像案例最好还是对照原版的。

二、知识概要：背景知识

1. 空间域（spatial domain）是指图像平面本身，基于空间域的图像处理直接以图像中的像素操作为基础。空间域这个术语其实是相对变换域（transform domain）中的图像处理而言的。关于二者的有关概念请参考《http://iyenn.com/rec/325695.html 图像处理空间域、变换域、时域和频域的含义理解：spatial VS transforms domain》的相关介绍。

2. 空间域图像处理（spatial processing）主要分为灰度变换（intensity transformations）和空间滤波（spatial filtering）两类。

3. 灰度变换在图像的单个像素上操作，主要以对比度操作（contrast manipulation ）和阈值处理（image thresholding）为目的。

4. 空间滤波如图像锐化（image sharpening）通过在图像中每个像素的邻域中工作来执行图像处理。

5. 空间域的图像处理可以使用如下公式表示：
   
   其中f(x,y)代表输入图像，g(x,y)是输出图像，T是在点（x,y）的邻域上定义的关于输入图像的运算。

6. 邻域是中心在点(x,y)的矩形，点（x,y）为邻域的原点，邻域运算以邻域原点从一个像素向另一个像素移动，对邻域中的像素执行运算T，并在原点位置产生目标图像在该点的输出，直到遍历图像中所有像素。当邻域的原点位于图像边界时，部分邻域将位于图像外部，这种情况进行邻域运算的处理时，要么忽略掉外部的点，要么就是将其灰度值作为0或指定某个固定灰度值参与运算，类似用0或固定灰度值填充图像外部的邻域范围。上述邻域运算处理过程就称为空间滤波（spatial filtering）。

7. 空间滤波的邻域和其上的邻域运算就称为空间滤波器（spatial filter ），也称为空间掩膜（spatial mask）、空间核（kernel）、空间模板（template）、空间窗口（window）。下图是点（x,y）的一个3×3的邻域，

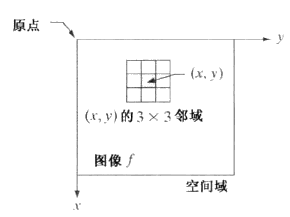
8. 最小的邻域大小为1×1，这种情况下，目标图像的像素值仅取决于输入图像相同位置像素的值以及滤波运算，而上面的式（3.1-1）则可以使用下式表示：
   
   上式中，r和s分别表述输入图像和输出图像在任意点处的灰度（intensity、gray-level），T称为灰度变换函数（intensity transformation function）。常见的如对比度拉伸（contrast stretching）与阈值处理函数（thresholding function）都是灰度变换函数。这种输出图像每个像素的灰度值结果仅取决于一个点处的灰度方法称为点处理技术（point processing techniques），而与大于1的邻域像素值相关的处理技术称为邻域处理技术（neighborhood processing techniques）。
   灰度变换是点处理技术，而邻域大小大于等于1×1的空间滤波处理为邻域处理技术。

9. 图像增强（image enhancement）是一种典型的灰度变换，它在对图像进行加工后，使结果图像对于特定的应用比原始图像更适合。无论使用何种应用或方法，图像增强都是图像处理中最具视觉吸引力的领域之一。

三、知识概要：一些基本的灰度变换函数（Intensity Transformation Functions）

3.1、概述

3.1-2的公式所代表的灰度变换是图像处理中最简单的技术，实际上是一种把像素值r映射到像素值s的一种变换。

图像增强是一种典型的灰度变换，以其为例来作为灰度变换的介绍。图3.3是图像增强的一些灰度变换函数曲线：

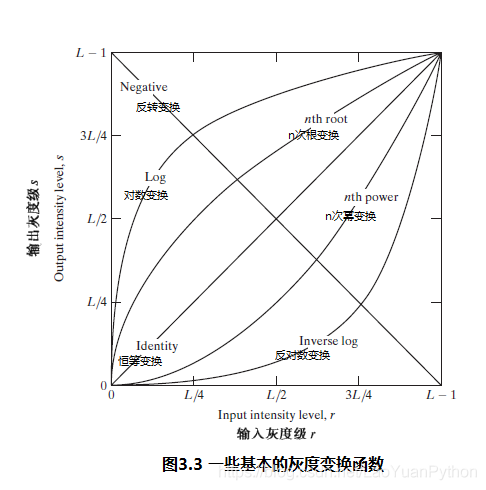
图像增强常用的三类基本函数包括：线性函数（如反转变换和恒等变换）、对数函数（对数和反对数变换）、幂律函数（n次幂和n次根变换）。其中的恒等函数是最没用的（trivial case），实际上就是输出图像等于输入图像的变换。

3.2、反转变换（Image Negatives）

反转变换就是负片特效（请参考《两行Python代码实现视频负片特效》的介绍）所使用的图像变换，其变换公式为： s = L - 1 - r ，其中r和s分别表述输入图像和输出图像在任意点处的灰度，L-1表示图像像素的最大灰度，如8bit图像L为256。

反转变换特别适合增强嵌入在一幅图像暗区域中的白色或灰色细节，特别是在黑色在图像范围占主导地位时。

下图左边的原图是一幅带有小块病变的乳房的X光照片，右图是反转变换后的图像，可以看到反转后病变部位更清晰：

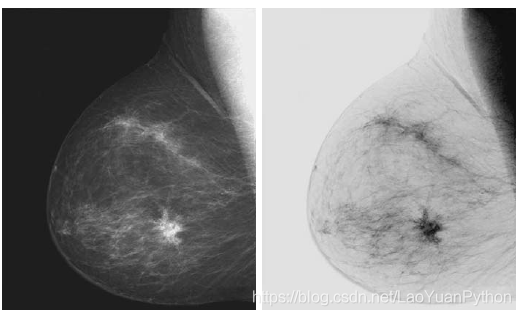
3.3、对数变换（Log Transformations）

3.3.1、概念

对数变换公式为：

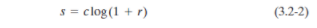
其中r和s分别表述输入图像和输出图像在任意点处的灰度，c是一个常数，一般取值为1。

老猿分析：对数变换为什么是log(1+r)而不是log（r）? 老猿认为这是因为无论底数是多少，log（1）都为0，而任何自然数为底小于1的正数为真数的对数值都小于0。

如果对数运算已经记不太清的博友，请参考《人工智能数学基础2：指数、方根及对数运算公式》的介绍。

从图3.3可以看出，对数变换将输入图像中范围较窄的低灰度值映射为了输出图像中范围较宽的灰度值，而反过来，输入图像中范围较宽的高灰度值映射为了输出图像中范围较窄的灰度值。因此对数变换可以用于扩展图像中暗像素的值和压缩图像中亮像素的灰度值。而反对数的变换则与此相反。

同时，对数函数压缩像素值变化比较大的图像的动态范围，即会使得大的图像动态范围变小。这是因为大于1的数求对后的结果比原值小。

注：老猿认为，反对数实际上就是指数，可以看到图3.3中的曲线，二者是相同的，如果底数相同，就是一回事。

3.3.2、对数变换案例

傅里叶频谱的动态范围很宽，从0到1000000甚至更高，图像显示不支持这么大范围的灰度值显示，只能在量化时将幅度值的基准刻度设置很大，这样就使得高灰度值的像素主导了图像的显示，使得中低灰度值变得与0灰度值难以区分，这样会导致图像细节的丢失。

以傅里叶频谱为例，如果对傅里叶频谱进行公式3.2-2的对数变换（设c=1），则可以大幅压缩图像的动态范围，使得图像的细节得以展示。下图左边是傅里叶频谱的图像，右边是进行了对数变换的傅里叶频谱图像：

3.4、幂律（伽玛）变换（Power-Law (Gamma) Transformations）

3.4.1、概念

幂律变换的基本形式为：

其中c和γ为常数，习惯上幂律变换的指数称为伽玛（gamma），因此幂律变换又称为伽玛变换。

下图是针对不同伽玛值输入图像灰度值r和输出图像灰度值s之间的幂律变换关系：

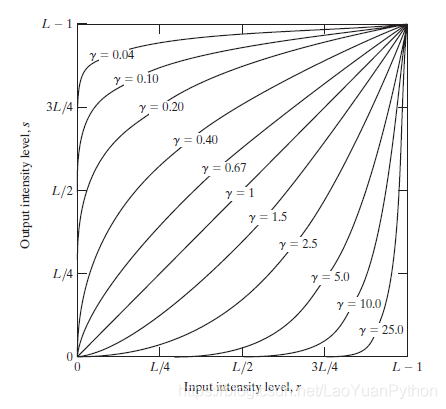
可以看到，γ值小于1时，幂律函数本质上就是n次根函数，当变量（底数）小于1时它使得函数结果值比输入变量值变大，底数大于1时使得函数结果值比输入变量值变小，因此γ值小于1时的幂律变换，可以使得较窄范围的暗色像素输入值映射为较广范围的输出值，而对高灰度值则会收窄其输出值范围。γ值大于1时则效果与此相反。而当c和γ都等于1时，幂律变换就是恒等变换（identity transformation）。

老猿分析：可以看到幂律变换某些时候的效果与对数变换效果类似，某些时候与其效果相反，这是因为指数函数与对数函数同底时是相反函数，而幂函数在底数某些取值范围内与固定的指数函数有相同的趋势，但对数变换对真数加了1，而幂律变换则没有类似处理。

3.4.2、 对数变换应用–伽马校正（Gamma correction）

图像获取、 打印和显示等设备的输入、 输出响应通常为非线性的, 满足幂律关系。 为了得到正确的输出结果而对这种幂律关系进行校正的过程称之为伽玛校正。例如阴极射线管（cathode ray tube，CRT）有个灰度到电压的响应（intensity-to-voltage response）就是一个指数变化范围为1.8~2.5的幂函数。从上面幂律变换γ=2.5曲线可以看到，在低灰度值时，幂律变换使得目标图像灰度值变得更小，因此会使得暗的图像更暗，亮的更亮。

下图4幅图像按从左到右再从上到下依次标记为a、b、c、d，a为原始图像，是一幅简单灰度斜坡渐变图像（intensity-ramp image），b为该图像在监视器上直接显示的效果，由于显示器的伽玛响应作用可以看到暗的部分变得更暗了。

为了修订，在将图像输入到显示器时，采用如下方式修正：

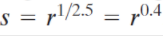
即进行伽玛值为0.4的伽玛变换，原图像使用上述伽玛变换后，变成了c所示图像，再将该图像输入到显示器进行显示，可以看到显示图像与原图像已经基本没什么区别了。

类似的扫描仪和打印机也有同样的情况，只是伽马值不同而已。

伽马校正不禁能改变图像的灰度，也能改变彩色图像的RGB分布比率，因为经过校正后，可以改变各通道的值，由于不是线性变化，导致三个通道的值与校正前比率不同。

3.4.3、 对数变换应用–暗图像对比度增强（Contrast enhancement）

除了伽玛校正外，幂律变换在对比度增强操作中也很有作用。当一幅图像整体偏暗时，图像的整体灰度动态范围偏小，且灰度值偏低，可以通过幂律变换扩展图像的灰度范围，此时需要使用指数为小于1的分数的幂律变换来完成。当然老猿认为也可以使用对数变换达成。

下图a为一幅核磁共振图(MRI，magnetic resonance image)，图中显示了人体胸部以上脊椎骨折错位和脊髓收到影响的情况，骨折位置在胸椎垂直中心附近（图中从上往下约1/4处）：

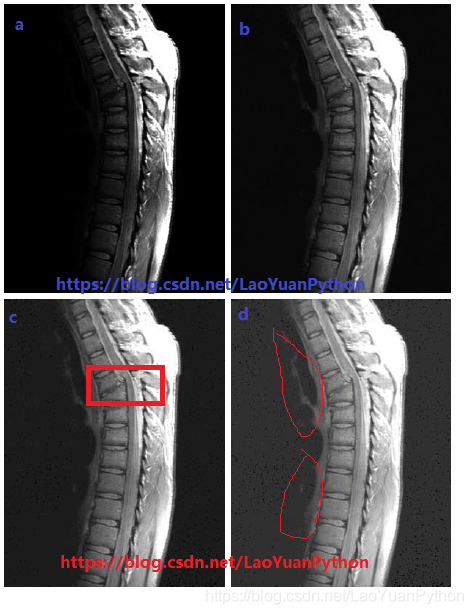
图像a整体偏暗，需要通过扩展灰度级提升对比度，用γ值分别为0.6、0.4、0.3对a图进行幂律变换，得到b、c、d三图。可以看到随着γ值的减小，更多的细节变得可见了，而0.3的γ值，背景中的细节有很小的进一步增强，但图像有轻微“褪色（washed-out）”的外观，特别是背景中老猿用红笔标记之处。在这幅图像中，γ=0.3是个近似的极限点，再低于该值对比度会下降到令人难以接受的程度。

注：骨折这个地方找了半天不能确认，老猿认为是C图中红色框范围内那处，请别人帮忙也不能确认。另外褪色的部分标记也是老猿自己理解的，不能确保是否正确，请大家自行理解。

3.4.3、 对数变换应用–亮图像对比度增强（Contrast enhancement）

亮图像对比度增强是和暗图像对比度增强相反的情况，原图像a像素的整体灰度值偏大，导致图像过亮，整体图像呈现“褪色（washed-out）”的外观，这时需要是的γ值大于1来压缩灰度级提升对比度。b、c、d是分别使用γ=3、4、5对图像a进行幂律变换后的结果图像。

γ=5时得到的图像d有些地方太暗，导致一些细节丢失，如左上方主路左侧的暗色区域。

3.5、分段线性变换函数（Piecewise-Linear Transformation Functions）

3.5.1 概念

分段线性变换是反转变换、对数变换以及幂律变换之外的补充方法，它将图像灰度区间分成两段甚至更多段，针对每段分别进行不同的灰度变换。方法实际上是增强原图各部分的反差，即增强输入图像中感兴趣的灰度区域，相对抑制那些不感兴趣的灰度区域。其优点是形式可以任意复杂，主要缺点是变换的需求需要相当多的用户输入。

3.5.2 分段线性变换应用1–对比度拉伸

下图是用于对比度拉伸的一个分段线性变换：

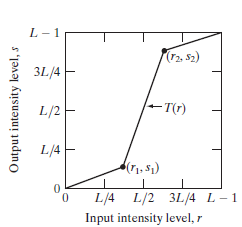
将输入图像的灰度分成三段，分别是[0，r1] 、(r1，r2]、(r2，L-1]，点（r1，s1）、（r2，s2）控制着变换函数的形状：

• 如果点（r1，s1）、（r2，s2）两者是同一个点，则变换为线性变换
• 如果r1=r2，s1=0,s2=L-1，则变换为阈值处理
• （r1，s1）、（r2，s2）的中间值产生输出图像不同程度的灰度值扩展，从而影响输出图像的对比度

下图a是一副电子显微镜扫描放大700倍的8比特低对比度的花粉图像：

对图像a进行如下分段线性变换：（r1,s1）= (min®,0)且（r2，s2）=(max®,L-1)，即将输入图像最小灰度值映射为0，最大灰度值映射为L-1=255，这样就将原图像的动态范围[min®，max®]扩大了输出图像的动态范围[0，L-1]。这样得到的图像就是上图b。

如果对图像a进行如下分段线性变换：（r1,s1）= (m,0)且（r2，s2）=(m,L-1)，m为图像的平均灰度值，这样处理就是上面介绍的阈值处理，得到的图像就是上图c。

3.5.3 分段线性变换应用2–灰度级分层（Intensity-level slicing）

突出图像中特定灰度范围的亮度通常很有趣，应用包括增强卫星图像中的大量水体等特征和增强X射线图像中的裂痕（flaws ），对应的处理通常称为灰度级分层（Intensity-level slicing）。

灰度级分层有多种方法实现，但它们都是如下两种基本方法的变形：

• 将感兴趣灰度范围内的灰度显示为一个值（如白色），其他灰度值显示为另一个值（如黑色），这样就产生了一副二值图（binary image）
• 将感兴趣灰度范围内的灰度显示为一个亮值或暗值，其他灰度级（Intensity-level）保持不变

这两种方式对应的变换曲线分别如下：

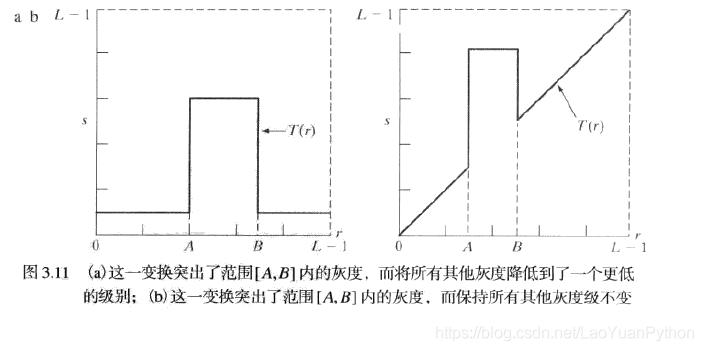
灰度级分层应用案例：

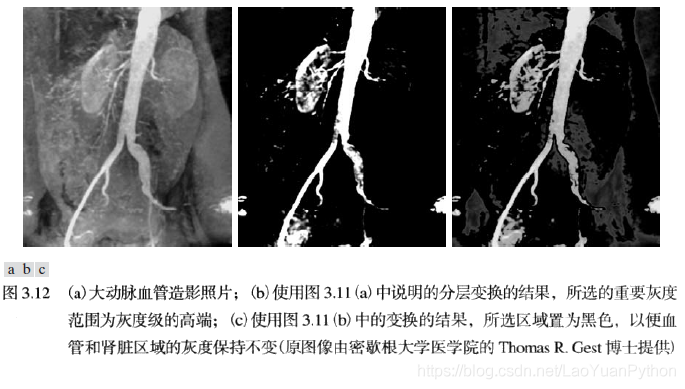
3.5.4 分段线性变换应用3–比特平面分层（Bit-plane slicing）

像素是由比特组成的数字，与灰度级分层不同的是，比特平面分层是用于突出特定比特位对总图像外观的贡献。

一8比特图像可以认为由8个1比特的平面构成：

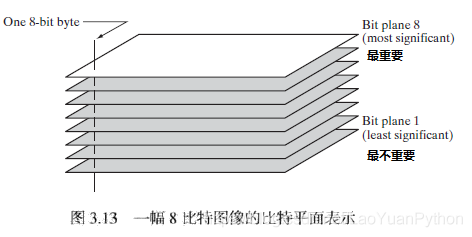
其中的比特平面1包含所有像素灰度值的最低一位比特，最不重要，比特平面8包含所有像素灰度值的最高一位比特，最重要。

下图a是一美钞数字图像，图b到图i分别代表其比特平面1到比特平面8：

可以看到后面4个高阶的比特平面，特别是最后两个最高阶的比特平面，包含了视觉上最重要的大多数数据，而低阶比特平面在图像中主要体现了更精细的灰度细节。

把一幅图像分解成比特平面，对于分析图像中每个比特的相对重要性很有用，可以帮助确认用于量化图像的比特数，此外，这种类型的分解对图像压缩也很有用。在图像压缩中，重建一幅图像所需要使用的比特平面比图像的全部平面少。例如用4个高阶比特平面来存储和重建图像，比存储整幅图像可以节省一半的空间，但图像的外观基本上没有大的变化。

为什么将比特平面分层放到分段线性函数的应用呢？这是因为要将比特平面拆分出来，需要用到分段函数，如拆分第8个比特平面时，将灰度值0-127之间的所有灰度值置为0,128-255之间的所有灰度值映射为1即可，这用阈值处理来实现即可。

四、小结及感悟

本部分主要对应第三章《3.1节 背景知识》和《3.2节 一些基本的灰度变换函数》，介绍了空间域、灰度变换、空间滤波、邻域的概念，结合案例介绍了灰度变换中的图像反转、对数变换、幂律变换、分段线性变换的原理和用途。

通过学习这些基本的概念，老猿第一次系统地理解了灰度变换，灰度变换大部分都是通过拉伸或压缩图像某些灰度值范围来提高图像的整体效果，对于提高图像的可辨识性具有重要的意义，这些简单的变换可以带来图像认知的质的提升。

更多图像处理请参考专栏《OpenCV-Python图形图像处理》及《图像处理基础知识》的介绍。

对于缺乏Python基础的同仁，可以通过老猿的免费专栏《 专栏：Python基础教程目录》从零开始学习Python。

如对文章内容存在疑问，可在博客评论区留言，或关注：老猿Python 微信公号发消息咨询。

写博不易，敬请支持：

如果阅读本文于您有所获，敬请点赞、评论、收藏，谢谢大家的支持！

关于老猿的付费专栏

1. 付费专栏《http://iyenn.com/index/link?url=https://blog.csdn.net/laoyuanpython/category_9607725.html 使用PyQt开发图形界面Python应用》专门介绍基于Python的PyQt图形界面开发基础教程，对应文章目录为《 http://iyenn.com/rec/324324.html 使用PyQt开发图形界面Python应用专栏目录》；
2. 付费专栏《http://iyenn.com/index/link?url=https://blog.csdn.net/laoyuanpython/category_10232926.html moviepy音视频开发专栏 )详细介绍moviepy音视频剪辑合成处理的类相关方法及使用相关方法进行相关剪辑合成场景的处理，对应文章目录为《http://iyenn.com/rec/324326.html moviepy音视频开发专栏文章目录》；
3. 付费专栏《http://iyenn.com/index/link?url=https://blog.csdn.net/laoyuanpython/category_10581071.html OpenCV-Python初学者疑难问题集》为《http://iyenn.com/index/link?url=https://blog.csdn.net/laoyuanpython/category_9979286.html OpenCV-Python图形图像处理 》的伴生专栏，是笔者对OpenCV-Python图形图像处理学习中遇到的一些问题个人感悟的整合，相关资料基本上都是老猿反复研究的成果，有助于OpenCV-Python初学者比较深入地理解OpenCV，对应文章目录为《http://iyenn.com/rec/324329.html OpenCV-Python初学者疑难问题集专栏目录 》
4. 付费专栏《http://iyenn.com/index/link?url=https://blog.csdn.net/laoyuanpython/category_10762553.html Python爬虫入门 》站在一个互联网前端开发小白的角度介绍爬虫开发应知应会内容，包括爬虫入门的基础知识，以及爬取CSDN文章信息、博主信息、给文章点赞、评论等实战内容。

前两个专栏都适合有一定Python基础但无相关知识的小白读者学习，第三个专栏请大家结合《http://iyenn.com/index/link?url=https://blog.csdn.net/laoyuanpython/category_9979286.html OpenCV-Python图形图像处理 》的学习使用。

对于缺乏Python基础的同仁，可以通过老猿的免费专栏《http://iyenn.com/index/link?url=https://blog.csdn.net/laoyuanpython/category_9831699.html 专栏：Python基础教程目录）从零开始学习Python。

如果有兴趣也愿意支持老猿的读者，欢迎购买付费专栏。

老猿Python，跟老猿学Python！

☞ ░ 前往老猿Python博文目录 https://blog.csdn.net/LaoYuanPython ░