一、引言

在图像处理以及人工智能中，“卷积”一词是非常重要的概念，也是初学者难以理解的地方。在《数字图像处理：理解什么是卷积（滤波）、卷积核以及相关参考资料》老猿结合相关知识详细介绍了卷积相关知识，这几天学习《数字图像处理》第三章《空间相关与卷积》才知道以前的知识虽然不能说错误，但也不能说完全准确。

二、空间相关和卷积的概念

2.1、简介

在执行线性空间滤波时，必须清楚地理解两个相近的概念。一个是相关(correlation)，另一个是卷积(Convolution)。卷积的概念是线性系统理论的基石。

如《《数字图像处理》空间滤波学习感悟1：空间滤波原理》介绍，滤波器模板移过图像并计算每个位置乘积之和的处理其实就是相关。

卷积与相关相似，但滤波器首先要旋转180°。

解释这两个概念的区别的最好方法是举一个例子，在此之前，我们先介绍一个重要概念：离散单位冲激。

2.2、离散单位冲激概念

离散单位冲激（discrete unit impulse）就是包含单个1其余都是0的函数。

老猿注：离散单位冲激，首先它是一个函数，而这个函数是一个由数字序列或数字矩阵表达的函数。discrete unit impulse，按英文字面意思可以称为离散单位脉冲，可以设想一个由一系列0和1表达的电波图形（函数图形），当该电波中只有一个坐标的值为1其余都为0时，该电波图形对应的函数就是离散单位冲激。

2.3、一维相关与卷积案例

我们从一个一维示例开始，下图3.29(a)显示了一个一维函数f和一个滤波器w，图3.29(b)显示了执行相关的起始位置。

图3.29(b)中，我们注意到f和w开始对齐位置中，f中存在未完全和w数据对应覆盖的部分，类似的在从w的倒数第二个数字和f的最后一个数字对齐时也未覆盖的部分。该问题的解决办法是在f的任意一侧补上足够的0（如果滤波器的尺寸是m，那么我们需要在f的两侧各补m-1个0），以便使 w 中的每一个像素都可访问到f中的每一个像素。图3.29©显示了适当填充过的函数。

当然零填充并不是唯一的选择（老猿认为：为了说明相关和卷积的概念，填0更直观）。例如。我们可在/的两侧复制第一个元素和最后一个元素m-1次，或镜像第一个元素和最后一个元素m-1次，并为填充使用镜像后的值。

相关处理过程：

1. 相关的第一个值是如图3.29©所示的初始位置的f和w的乘积之和(乘积之和为0)。这相当于位移x=0；
2. 为了得到相关的第二个值，我们把 w 向右移动一个像素位置(位移x=1)，并计算乘积之和，结果还是0；
3. 重复w向右移动过程中，当x=3时才第一次出现非零结果，在这种情况下，w中的8覆盖f中的1，相关的结果是8。 按这种方法进行，我们可以得到图3.29(g)中的全部相关结果；
4. 通常情况下，会将相关的结果数据大小保持与函数f一致，这样我们需要将全部相关的结果进行裁剪（老猿理解一般是左右两侧各裁剪相同大小，该大小应该为前面f两侧补0个数的一半），图3.29(h)就是裁剪后的结果。

注意：

1. 从上述过程中可以看到，可以看到相关处理过程中，x取了12个值(即x=0，1，2，…，11)，这样使w滑过f、以便w中的每一个像素访问f中的每一个像素。相关的第一个值对应于滤波器的零位移，第二个值对应于一个单元位移，等等，因此相关是滤波器位移的函数。
2. 滤波器 w与包含有全部0和单个1的离散单位冲激函数相关，得到的结果就是 w的一个拷贝，但旋转了180°（即数字序列倒转）。因此一个函数与离散单位冲激相关，在该冲激位置产生这个函数的一个翻转的版本；
3. 如果预先旋转滤波器，并执行相同的滑动乘积求和操作，就能得到原函数f的一个拷贝，这个过程就是卷积。卷积的基本特性是某个函数与某个单位冲激卷积，得到一个在该冲激处的这个函数的拷贝。如图3.29右边一列所示的那样。由此，我们看到，为了执行卷积，需要做的是把一个函数旋转180°（旋转180°即水平翻转对应函数），然后执行相关中的相同操作。正如其结果所示，旋转两个函数的做法没有区别。

2.3、二维图像相关与卷积案例

上述一维相关与卷积的案例及概念很容易扩展到二维图像。对于大小为mxn的滤波器，我们在图像的顶部和底部至少各填充m-1行0、左侧和右侧各填充n-1列0，以二维的仅包含一个1其余全为0的核矩阵代替一维的序列，就可以以图像矩阵和核矩阵进行相关和卷积的处理。

以一个5×5的图像矩阵和一个3×3的核矩阵为例，其相关和卷积处理过程如下图3.30所示：

图3.30（c）显示了执行相关操作的滤波器模板的初始位置；图3.30(d)显示了所有相关操作的结果；图3.30(e)显示了裁剪后的相应结果。图3.30(f)到(h)显示了卷积的结果。

从图3.30可以看出：

1. 对于相关，与一维数据一样，二维图像矩阵相关的结果旋转了180°；
2. 对于卷积，与一维数据一样，在预先旋转模板然后使用刚才描述的方法对乘积做滑动求和操作后，一个函数与一个冲激卷积，在该冲激的位置复制了这个函数；
3. 很容易想到，如果滤波器模板是对称的，相关和卷积将得到相同的结果；
4. 在二维情况下，旋转180°等同于沿一个坐标轴翻转模板，然后沿另一个坐标轴再次翻转模板。

三、相关和卷积的公式表示

3.1、相关的表示

一个大小为m×n的滤波器w(x,y)与一幅图像f(x,y)做相关操作，可以表示为：
w(x, y)☆f(x, y)，其计算方法就是在《数字图像处理》空间滤波学习感悟1：空间滤波原理》中介绍的滤波公式：

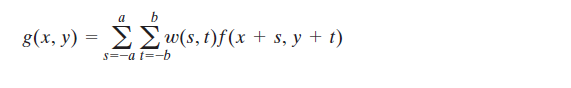
因此有如下公式：

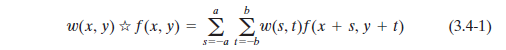
这一公式对所有位移变量x和y求值，以便w的所有元素访问f（假设f已经适当填充）的每一个元素。在上述公式中，a=(m-1)/2、b=(n-1)/2。

3.2、卷积的表示

滤波器w(x,y)与一幅图像f(x,y)做卷积操作，可以表示为：w(x, y)★f(x, y)，对应表示公式为：

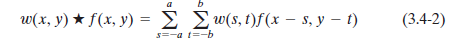
式3.4.2右边的减号表示翻转f（旋转180°）。虽然翻转f和w效果是一样的，但一般惯例是翻转w。这一公式同样对所有位移变量x和y求值，以便w的所有元素访问f（假设f已经适当填充）的每一个元素。

四、小结

本文介绍了空间滤波中的两个重要基础概念：相关和卷积，并介绍了使用式3.4-1和式3.4-2来表述这两个操作，在实践中，对于相关和卷积通常用同一个算法实现式3.4-1，如果要执行相关，可以将滤波器w输入到算法中，如果要执行卷积，则可以将旋转180°的w输入到算法中。当然也可以用算法实现式3.4-2，只是输入恰好与相关相反。

使用相关或卷积执行空间滤波是优先选择的方法，无论是式3.4-1还是式3.4-2，都可以通过简单的旋转滤波器去执行相关或卷积的功能。在空间滤波任务中，重要的是按期望操作的方式来确定滤波器模板（filter mask）。

在图像处理文献中，经常使用卷积滤波器（convolution filter）、卷积模板（convolution mask ）或卷积核（ convolution kernel）这些术语，按照惯例，这些术语都是用于表示一种空间滤波器（spatial filter），并且该滤波器不一定真正用于卷积处理。类似地，模板与图像的卷积（convolving a mask with an image）通常用于表示前面介绍的滑动乘积求和（sumof-products process）的处理，而不必区分相关与卷积的区别，更合适的是，它通常用于表示相关与卷积两者操作之一，这一不太严密的术语很容易产生理解的歧义。

另外本文中介绍的一个函数与单位冲激的卷积，相当于在单位冲激位置复制该函数，这一特性将在大量的推导中扮演核心角色。

更多图像处理请参考专栏《OpenCV-Python图形图像处理》及《图像处理基础知识》的介绍。

对于缺乏Python基础的同仁，可以通过老猿的免费专栏《 专栏：Python基础教程目录》从零开始学习Python。

如对文章内容存在疑问，可在博客评论区留言，或关注：老猿Python 微信公号发消息咨询，也可以扫描博客左边栏目的微信公号二维码咨询。

写博不易，敬请支持：

如果阅读本文于您有所获，敬请点赞、评论、收藏，谢谢大家的支持！

关于老猿的付费专栏

1. 付费专栏《http://iyenn.com/index/link?url=https://blog.csdn.net/laoyuanpython/category_9607725.html 使用PyQt开发图形界面Python应用》专门介绍基于Python的PyQt图形界面开发基础教程，对应文章目录为《 http://iyenn.com/rec/324324.html 使用PyQt开发图形界面Python应用专栏目录》；
2. 付费专栏《http://iyenn.com/index/link?url=https://blog.csdn.net/laoyuanpython/category_10232926.html moviepy音视频开发专栏 )详细介绍moviepy音视频剪辑合成处理的类相关方法及使用相关方法进行相关剪辑合成场景的处理，对应文章目录为《http://iyenn.com/rec/324326.html moviepy音视频开发专栏文章目录》；
3. 付费专栏《http://iyenn.com/index/link?url=https://blog.csdn.net/laoyuanpython/category_10581071.html OpenCV-Python初学者疑难问题集》为《http://iyenn.com/index/link?url=https://blog.csdn.net/laoyuanpython/category_9979286.html OpenCV-Python图形图像处理 》的伴生专栏，是笔者对OpenCV-Python图形图像处理学习中遇到的一些问题个人感悟的整合，相关资料基本上都是老猿反复研究的成果，有助于OpenCV-Python初学者比较深入地理解OpenCV，对应文章目录为《http://iyenn.com/rec/324329.html OpenCV-Python初学者疑难问题集专栏目录 》
4. 付费专栏《http://iyenn.com/index/link?url=https://blog.csdn.net/laoyuanpython/category_10762553.html Python爬虫入门 》站在一个互联网前端开发小白的角度介绍爬虫开发应知应会内容，包括爬虫入门的基础知识，以及爬取CSDN文章信息、博主信息、给文章点赞、评论等实战内容。

前两个专栏都适合有一定Python基础但无相关知识的小白读者学习，第三个专栏请大家结合《http://iyenn.com/index/link?url=https://blog.csdn.net/laoyuanpython/category_9979286.html OpenCV-Python图形图像处理 》的学习使用。

对于缺乏Python基础的同仁，可以通过老猿的免费专栏《http://iyenn.com/index/link?url=https://blog.csdn.net/laoyuanpython/category_9831699.html 专栏：Python基础教程目录）从零开始学习Python。

如果有兴趣也愿意支持老猿的读者，欢迎购买付费专栏。

老猿Python，跟老猿学Python！

☞ ░ 前往老猿Python博文目录 https://blog.csdn.net/LaoYuanPython ░