
一、引言
在《人工智能数学基础—定积分1:定积分的概念以及近似计算》介绍了定积分的概念、几何意义、用定义来求定积分的案例以及使用矩形法、梯形法和抛物线法求定积分近似值的方法和案例等基础知识,根据上文的介绍,结合相关知识补充如下2条规则:

可以知道,交互积分区间的上下限,则定积分的绝对值不变但符号相反。
二、性质
2.1、性质1:定积分的线性运算
设α和β为常数,函数f(x)和g(x)在区间[a,b]上可积,则:
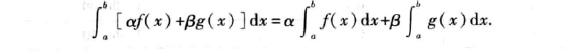
即定积分满足加法和数乘的线性运算规则,证明过程如下:

上述公式中λ为可积区间分成n分后的最大区间值。
实际上,该规则对于任意有限个可积函数的线性组合同样成立。
2.2、性质2:积分区间可加性
设函数f(x)在区间[a,b]上可积,设a
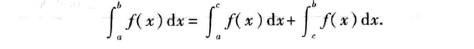
这个证明很简单,根据定积分的定义及极限即可以快速证明。
实际上,根据积分的补充规则,上述公式对于不满足a 如函数f(x)在区间[a,b]上恒等于1,则: 如果函数f(x)在区间[a,b]上恒大于等于0,则: 推论1:如果在区间[a,b]上函数f(x)≤g(x)且二者可积,则: 推论2:如果在区间[a,b]上函数f(x)可积,则: 设M和m是函数f(x)在区间[a,b]上的最大值和最小值,且函数f(x)可积,则: 如果函数f(x)在区间[a,b]上连续,那么在区间[a,b]上至少存在一点ξ,使得: 证明: 因此根据性质5有: 说明:无论a>b还是a 积分中值公式有如下的几何解释:在区间[a,b]上至少存在一点ε,使得以区间[a,b]为底边、以曲线y=f(x)为曲边的曲边梯形的面积等于同一底边而高为f(ε)的一个矩形的面积(图5-5)。 本文介绍了定积分的性质,包括线性组合运算、保号性、区间可加性、积分中值定理等。 本文内容是老猿学习同济版高数的总结,有需要原教材电子版以及OpenCV、Python基础知识、、图像处理原理介绍相关电子资料,或对文章内有有疑问咨询的,请扫博客首页左边二维码加微信公号,根据加微信公号后的自动回复操作。 更多人工智能数学基础请参考专栏《人工智能数学基础》。 如果阅读本文于您有所获,敬请点赞、评论、收藏,谢谢大家的支持! 前两个专栏都适合有一定Python基础但无相关知识的小白读者学习,第三个专栏请大家结合《http://iyenn.com/index/link?url=https://blog.csdn.net/laoyuanpython/category_9979286.html OpenCV-Python图形图像处理 》的学习使用。 对于缺乏Python基础的同仁,可以通过老猿的免费专栏《http://iyenn.com/index/link?url=https://blog.csdn.net/laoyuanpython/category_9831699.html 专栏:Python基础教程目录)从零开始学习Python。 如果有兴趣也愿意支持老猿的读者,欢迎购买付费专栏。2.3、性质3:恒等于1的函数积分

2.4、性质4:积分保号性
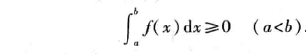
根据积分定义即可证明。
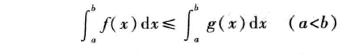
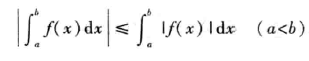
2.5、性质5:有界函数的积分
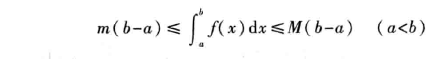
根据这个性质,可以根据被积函数的最大值和最小值,估算积分值的范围。
证明:

2.6、性质6:定积分中值定理
2.6.1、定理

这个公式叫做积分中值公式。其中:

称为函数f(x)在区间[a,b]上的平均值。
由《人工智能数学基础6:极限、极限运算、ε-δ语言、ε-N语言、级数和函数连续性》介绍可知,闭区间上的连续函数在该区间上一定有界,存在最大值M、最小值m,且有介值性。
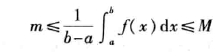
这表明,而:

一定是一个确定的值,按照连续函数介值性,则在区间[a,b]上至少存在一点ε,使得:

两边乘以b-a即可得证。2.6.2、几何解释

三、小结
说明:
写博不易,敬请支持:
关于老猿的付费专栏
老猿Python,跟老猿学Python!
☞ ░ 前往老猿Python博文目录 https://blog.csdn.net/LaoYuanPython ░

 微信公众号
微信公众号


评论记录:
回复评论: