人工智能数学基础-线性代数4：矩阵及矩阵运算

☞ ░ 老猿Python博文目录░

本节用到了行列式的相关知识，而在行列式中用到了矩阵知识，但总体来说先介绍矩阵再介绍行列式更合适一些，行列式的知识大家只需要知道一个矩阵A对应的行列式记为符号|A|，其结果为一个标量，具体内容请见下节。

一、矩阵定义

矩阵（Matrix）是一个按照长方阵列排列的复数或实数集合，定义如下：
由 m × n 个数aij排成的m行n列的数表称为m行n列的矩阵，简称m × n矩阵。记作：
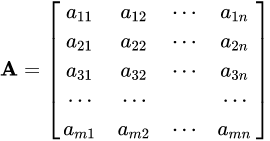
在这里插入图片描述

这m×n 个数称为矩阵A的元素，简称为元，数aij位于矩阵A的第i行第j列，称为矩阵A的(i,j)元，以数 aij为(i,j)元的矩阵可记为(aij)或(aij)m × n，m×n矩阵A也记作Amn。

元素是实数的矩阵称为实矩阵，元素是复数的矩阵称为复矩阵。而行数与列数都等于n的矩阵称为n阶矩阵或n阶方阵。

对于一个m×n 的矩阵A中某行的所有n个元素组成的n维向量叫做A的行向量，由A中某列的所有m个元素组成的m维向量叫做A的列向量。

A中的第i个行向量横写成：(ai1…ain)
第j个列向量竖写成：
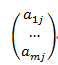
在这里插入图片描述
有时为了方便也横写。

只有一行一列的矩阵通常也可以叫做向量。

二、矩阵的秩

2.1、定义

一个矩阵,它的列矢量的极大无关组中矢量的个数叫做列秩,行矢量的极大无关组中矢量的个数叫做行秩,而它最大的且不等于0的子行列式的阶数r叫做它的秩。

可以证明,矩阵的行秩等于列秩等于秩,对于m×n矩阵而言,若 r=min(m,n) ,则称之为满秩矩阵，否则就叫降秩矩阵。矩阵A的秩用秩A表示，也可以用rank A表示。

对n阶方阵A,若rank A=n,则称A为非奇异矩阵（nonsingular matrix），否则称为奇异矩阵（singular matrix）。奇异矩阵对应行列式为0。可逆方阵就是非奇异矩阵，非奇异矩阵也是可逆矩阵。

2.2、关于矩阵秩的定理和属性

2.2.1、几个定理
  1. 定理1：（m,n）-矩阵A的m个行向量线性相关的充要条件是A的秩小于m；
  2. 定理2：（m,n）-矩阵A的秩等于r的充要条件是A中有r个行（列）向量线性无关，并且任意r+1个行（列）向量都线性相关；
  3. 定理3：假定a1,…,an是n个向量，β1…βm都是a1,…,an的线性组合。如果m>n，那么β1…βn线性相关。
  4. 定理4：假如矩阵A经过若干个行初等变换（如互换两行、用一个不为0的数乘某行、或者某行加到另一行等）变为矩阵B，那么A、B的秩相等
  5. 定理5：满秩矩阵用行初等变换可以变为单位矩阵。
2.2.2、矩阵初等变换

互换矩阵的两行、用一个不为零的数乘A的一行以及用一个数乘A的一行加到另一行上，这些变换叫做A的行初等变换。类似的，还有矩阵的列初等变换。二者统称为矩阵A的初等变换。

假如矩阵A经过若干个行初等变换变为矩阵B，则A和B的秩相等。

三、矩阵的运算

矩阵的基本运算包括矩阵的加法、减法、数乘、乘法、转置。

3.1、矩阵的加减法

3.1.2、矩阵加减法运算

矩阵的加减法是两个同型矩阵（行数、列数相同）之间的加减法，两个m×n矩阵A和B的和，标记为A+B，差记为A-B，对应结果都是m×n矩阵，其内的各元素为A、B各相同位置元素进行加减后的值。

矩阵加法满足交换律和结合律：
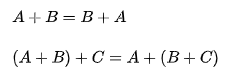
在这里插入图片描述

3.1.2、负矩阵

负矩阵属于矩阵算法中的一种，用于规定矩阵减法，设矩阵A（有i行j列的矩阵），那么A的负矩阵就是-A（A的每个（i,j）元 都变为其相反数）。

3.2、矩阵的数乘

3.2.1、定义

矩阵的k倍数乘，是以一个实数k与矩阵A相乘，其结果B是与A同型矩阵，B的每个元素都是A相同位置元素乘以k的结果。矩阵数乘本质上是在矩阵的每个元素上乘了一个k，用向量的数乘来解释，即是对每个行向量乘了k, 或者也相当于对每个列向量乘了k。

3.2.2、矩阵数乘运算定律

设A、B为矩阵，m、n为实数，则：

  • （mn）A=m(nA)
  • (m+n)A =mA + nA
  • m(A+B) = mA + mB

矩阵的加减法和数乘运算称为矩阵的线性运算。

3.3、矩阵乘法

3.3.1、乘法定义

矩阵相乘最重要的方法是一般矩阵乘积。它只有在第一个矩阵的列数和第二个矩阵的行数相同时才有意义。
设A为 m×p的矩阵，B为p×n 的矩阵，那么称m×n 的矩阵C为矩阵A与B的乘积，记作 C=AB，其中矩阵C中的第i行第j列元素等于矩阵A的第i行的元素与矩阵B的第j列对应元素乘积之和。可以表示为：
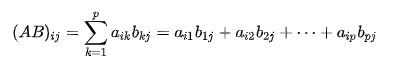
在这里插入图片描述
矩阵C的行数等于矩阵A的行数，C的列数等于B的列数。
如：
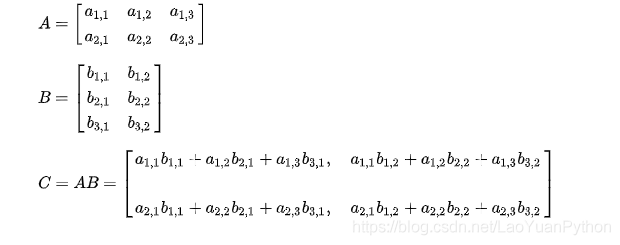
在这里插入图片描述

3.3.2、乘法定律
  • 乘法结合律： (AB)C=A(BC)
  • 乘法左分配律：(A+B)C=AC+BC
  • 乘法右分配律：C(A+B)=CA+CB
  • 对数乘的结合性k(AB）=(kA)B=A(kB）
  • 转置 (AB)T=BTAT

另外矩阵乘法在以下两种情况下满足交换律：

  • AA*=A*A，A和伴随矩阵相乘满足交换律
  • AE=EA，A和单位矩阵或数量矩阵满足交换律。

更多矩阵乘法的介绍请参考《百度百科关于矩阵乘法的介绍》。

3.4、矩阵转置

设A为m×n阶矩阵（即m行n列），第i 行j 列的元素是a(i,j)，即：
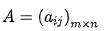
在这里插入图片描述
把m×n矩阵A的行换成同序数的列得到一个n×m矩阵，此矩阵叫做A的转置矩阵，记做AT或A’
例如矩阵:
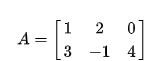
在这里插入图片描述
的转置矩阵为：
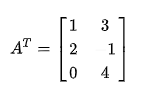
在这里插入图片描述
矩阵与其转置矩阵的秩相等。

矩阵的转置且满足下列运算运算定律：
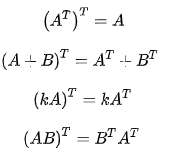
在这里插入图片描述
矩阵乘法的更多介绍请参考《百度百科矩阵乘法介绍》。

3.5、关于矩阵运算的有关补充

  • 矩阵A+B的秩小于A的秩+B的秩
  • 矩阵A、B的乘积的秩不大于A的秩与B的秩
  • |kA| = kn|A|
  • 对于n阶方阵A，存在正整数k，使得Ak=0，这样的方阵A就叫做幂零矩阵。满足条件的最小的正整数k被称为A的度数或指数，这里的0是指所有元都为0的零矩阵。
  • 两个满秩矩阵的乘积仍是满秩矩阵
  • 两个n阶方阵A、B的乘积AB的行列式等于A的行列式乘B的行列式，即|AB|=|A|×|B|
  • 矩阵A、B的乘积的转置矩阵(AB)‘等于B的转置矩阵B’和A的转置矩阵A’的乘积，即：(AB)’=B’A’

四、部分特殊矩阵

4.1、单位矩阵

在矩阵的乘法中，有一种矩阵起着特殊的作用，如同数的乘法中的1，这种矩阵被称为单位矩阵。它是个方阵，从左上角到右下角的对角线（称为主对角线）上的元素均为1。除此以外全都为0。

主对角线上的元素都为1，其余元素全为0的n阶矩阵称为n阶单位矩阵，记为 In或 En，通常用I或E来表示。

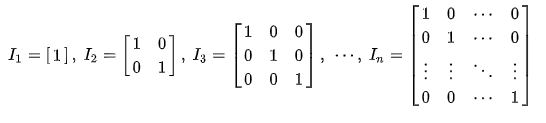
在这里插入图片描述

4.2、逆矩阵和伴随矩阵

4.2.1、逆矩阵定义

设A是一个n阶矩阵，若存在另一个n阶矩阵B，使得： AB=BA=E ，则称方阵A可逆，并称方阵B是A的逆矩阵，记为：
A = B-1
B = A-1

4.2.2、逆矩阵性质
  • A与B的地位是平等的，故A、B两矩阵互为逆矩阵，也称A是B的逆矩阵
  • 单位矩阵的逆矩阵是它本身
  • 零矩阵是不可逆的，即取不到B，使OB=BO=E
  • 如果A可逆，那么A的逆矩阵是唯一的
  • 若A可逆,则AT亦可逆,且(AT)-1=(A-1)T
  • 若A、B为同阶方阵且均可逆，则AB亦可逆,且(AB)-1=B-1 A-1
  • 矩阵A是可逆矩阵的充要条件是A为满秩矩阵
  • |A-1|=|A|-1，即A的逆矩阵的行列式等于A的行列式的-1次方，也即等于A的行列式的倒数

4.3、对角形矩阵和数量矩阵

除主对角线上的元外其他元都是0的n阶方阵称为对角形矩阵。

数量矩阵就是对角线上元素都是同一个数值，其余元素都是零。
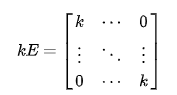
设E是单位矩阵, k是任何实数,则kE就是数量矩阵（数乘运算请参考下面矩阵运算部分的介绍）。
在这里插入图片描述

4.2.3、伴随矩阵定义

设A是一个n阶方阵，A=(aij)n×n，在行列式的章节中我们介绍过，将矩阵A 的元素aij 所在的第i行第j列元素划去后，剩余的各元素按原来的排列顺序组成的n-1阶矩阵所确定的行列式为元素 aij的余子式，记为 Mij，其对应的代数余子式：
Aij=（-1）i+jMij。

方阵A 的各元素的代数余子式Aij 所构成的如下矩阵 A*：

在这里插入图片描述
该矩阵 A*称为矩阵 A的伴随矩阵。

4.2.3、伴随矩阵性质
  • 如果 A可逆，则 A*=|A|A-1
  • |A*| = |A|n-1
  • (kA)* = kn-1A *
  • 若A可逆，则(A-1)* = (A*)-1
  • (AT)* = (A*)T
  • (AB)* = B* A*,实际上该公式可以扩展到多个矩阵的情况，多个矩阵的乘积的伴随矩阵等于这些矩阵的伴随矩阵逆序的乘积
  • AA* = A* A=|A|E
    从该公式可以看出，矩阵A如果是可逆矩阵，则：
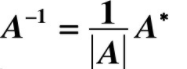
    在这里插入图片描述

4.4、三角形矩阵

主对角线以下或以上的全体元素都是零的n阶方阵称为三角形矩阵。形如：
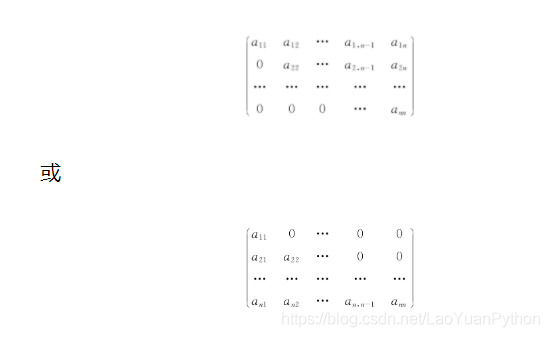
在这里插入图片描述
主对角线以上的全体元素都是零的n阶方阵称为上三角形矩阵，亦称上三角矩阵。

主对角线以下的全体元素都是零的n阶方阵称为下三角形矩阵，亦称下三角矩阵。

上三角形矩阵和下三角形矩阵统称三角形矩阵。

主对角元全是1的三角形矩阵称为特殊三角形矩阵。

主对角元全为零的三角形矩阵称为严格三角形矩阵。

两个n阶上(下)三角形矩阵的和、积以仍是上(下)三角形矩阵。

4.5、分块矩阵

4.5.1、定义

将一个矩阵用若干条横线和竖线分成许多个小矩阵，将每个小矩阵称为这个矩阵的子块，以子块为元素的形式上的矩阵称为分块矩阵。

4.5.2、运算规则

在这里插入图片描述
对于乘法来说进一步解释如下：
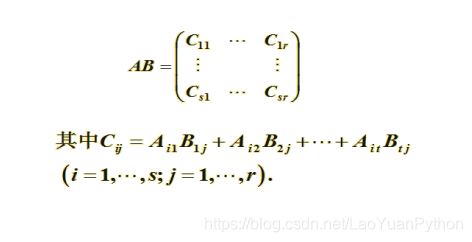
在这里插入图片描述
在这里插入图片描述
老猿总结：

分块矩阵加减法、数乘、转置、乘法的运算，可以将分块的子矩阵看做矩阵的元素，其运算规则与矩阵元素运算规则相同。但乘法要注意分块合适，且相关运算符合乘法的要求，即被乘数矩阵的列等于乘数矩阵的行数。

4.6、分块对角矩阵

4.6.1、定义

分块对角矩阵也称为准对角矩阵，是一种特殊的分块矩阵，设A为n阶方阵，若A的分块矩阵在非主对角线上的子块皆为零矩阵，且在主对角线上的子块都是方阵，即：
在这里插入图片描述
其中O表示零矩阵， Ai(i=1,2,…,s)都是方阵，那么称A为分块对角矩阵，该形状称为分块对角形。

4.6.2、性质

针对上述分块对角矩阵，有如下性质：

  • |A| = |A1| |A2|… |AS|

  • 如果Ai≠0(i=1,2,…,s)，则A可逆，且：
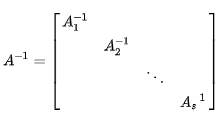
    在这里插入图片描述

  • 同结构的准对角矩阵的和、差、积、数乘及逆仍是准对角矩阵，且运算表现为对应子块的运算。假设：
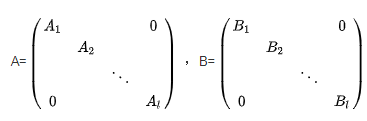
    在这里插入图片描述

  1. 两同型准对角矩阵的和仍为同形准对角矩阵
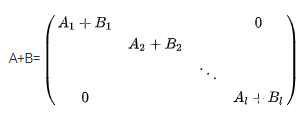
    在这里插入图片描述

  2. 两同型准对角矩阵的积仍为同形准对角矩阵
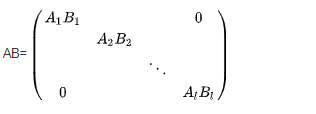
    在这里插入图片描述

  3. 一个数与准对角矩阵的乘积仍为同形准对角矩阵
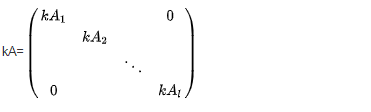
    在这里插入图片描述

  4. 准对角矩阵可逆的充分必要条件是：每个Ai（i=1，2，…，l）都可逆

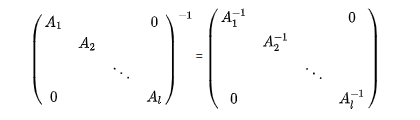
在这里插入图片描述

4.7、矩阵的标准形

一个矩阵只有前面某些第i行、第i列上的数是1，其余都是零的简单形状叫做矩阵的标准形。如4×5阶方阵对角线上a11、a22、a33为1，a44为0、a45以及其他元素都为0的矩阵就是标准形。

任意矩阵都可以用初等变换化为标准形。

4.8、对称矩阵和反对称矩阵

对称矩阵（Symmetric Matrices）是指以主对角线为对称轴，各元素对应相等的矩阵，即矩阵元素aij = aji

  1. 对于任何方形矩阵X，X+XT是对称矩阵
  2. A为方形矩阵是A为对称矩阵的必要条件
  3. 对称矩阵A与其转置矩阵A’相等

设A为n维方阵，若有A’=-A，则称矩阵A为反对称矩阵。对于反对称矩阵，它的主对角线上的元素全为零，而位于主对角线两侧对称的元反号。

4.9、正交矩阵和正交条件

n阶实矩阵A和其转置矩阵A’如果满足：AA’=A’A=E，则n阶实矩阵A称为正交矩阵，正交矩阵通常用字母Q表示。

根据定义可以知道，对于正交矩阵A=(aij),i,j∈[1,n]，则：

  1. a²1i+a²2i+…+a²ni = 1
  2. a²i1+a²i2+…+a²in = 1
  3. 当i≠j时，a1ia1j+a2ia2j+…+ani anj= 0
  4. 当i≠j时，ai1aj1+ai2aj2+…+ain ajn= 0

这是正交矩阵元素间的重要性质，也称为正交条件。

如下三个矩阵都是正交矩阵：
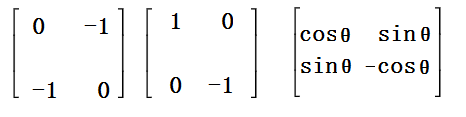
在这里插入图片描述
正交矩阵性质：
假设A是正交矩阵，A’是A的转置矩阵，则：

  1. A’是正交矩阵
  2. A和A’的各行是单位向量且两两正交
  3. A和A’的各列是单位向量且两两正交
  4. |A|=1或-1，如果正交矩阵的行列式为+1，则称之为特殊正交矩阵
  5. A’=A-1,即正交矩阵的转置矩阵与其逆矩阵相等
  6. 正交矩阵的逆是正交矩阵，两个正交矩阵的积是正交矩阵、
  7. 正交矩阵互换两行或两列还是正交矩阵

4.10、初等矩阵

初等矩阵是指由单位矩阵经过一次初等变换得到的矩阵。初等矩阵的模样可以写一个3阶或者4阶的单位矩阵。

定理：任意矩阵A经过行（列）初等变换成的矩阵等于用初等矩阵左（右）乘A的乘积

五、矩阵等价

  • 定义
    如果矩阵A经过有限次初等变换转换为矩阵B，就称A与B等价，表示为：
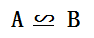
    在这里插入图片描述

定理1：两个矩阵等价的充要条件就是二者的秩相等。

  • 自反律：矩阵A和自身等价；
  • 对称律：如果A等价于B，则B等价于A；
  • 传递律：如果A等价于B，B等价于C，则A等价于C。

定理2：两个矩阵等价的充要条件就是存在两个满秩矩阵P、Q，使得：B = PAQ

定理3：对于矩阵A、B，B是满秩矩阵，那么AB或BA的秩与A的秩相等。

  • 如果两个矩阵行数和列数相等则称两个矩阵同型
  • 一个矩阵的元全是实数，则该矩阵称为实矩阵
  • 矩阵的元都是零的矩阵称为零矩阵
  • 把矩阵A的各元变号得到的矩阵，叫做A的负矩阵，用-A表示；
  • n阶矩阵A主对角线上n个数的和叫做矩阵A的迹，用tr(A)表示

定理4：矩阵A是满秩矩阵的充要条件是它能够表示为初等矩阵的乘积

六、小结

本文介绍了矩阵的定义、几种特殊矩阵、矩阵的秩等概念，并介绍了矩阵的加法、减法、数乘和乘法运算，由于向量可以看做单行或单列的矩阵，因此矩阵也可以用于向量运算。

写博不易，敬请支持：

如果阅读本文于您有所获，敬请点赞、评论、收藏，谢谢大家的支持！

更多人工智能数学基础的介绍请参考专栏《人工智能数学基础 》
专栏网址：http://iyenn.com/index/link?url=https://blog.csdn.net/laoyuanpython/category_10382948.html

关于老猿的付费专栏

  1. 付费专栏《http://iyenn.com/index/link?url=https://blog.csdn.net/laoyuanpython/category_9607725.html 使用PyQt开发图形界面Python应用》专门介绍基于Python的PyQt图形界面开发基础教程，对应文章目录为《 http://iyenn.com/rec/324324.html 使用PyQt开发图形界面Python应用专栏目录》；
  2. 付费专栏《http://iyenn.com/index/link?url=https://blog.csdn.net/laoyuanpython/category_10232926.html moviepy音视频开发专栏 )详细介绍moviepy音视频剪辑合成处理的类相关方法及使用相关方法进行相关剪辑合成场景的处理，对应文章目录为《http://iyenn.com/rec/324326.html moviepy音视频开发专栏文章目录》；
  3. 付费专栏《http://iyenn.com/index/link?url=https://blog.csdn.net/laoyuanpython/category_10581071.html OpenCV-Python初学者疑难问题集》为《http://iyenn.com/index/link?url=https://blog.csdn.net/laoyuanpython/category_9979286.html OpenCV-Python图形图像处理 》的伴生专栏，是笔者对OpenCV-Python图形图像处理学习中遇到的一些问题个人感悟的整合，相关资料基本上都是老猿反复研究的成果，有助于OpenCV-Python初学者比较深入地理解OpenCV，对应文章目录为《http://iyenn.com/rec/324329.html OpenCV-Python初学者疑难问题集专栏目录 》。

前两个专栏都适合有一定Python基础但无相关知识的小白读者学习，第三个专栏请大家结合《http://iyenn.com/index/link?url=https://blog.csdn.net/laoyuanpython/category_9979286.html OpenCV-Python图形图像处理 》的学习使用。

对于缺乏Python基础的同仁，可以通过老猿的免费专栏《http://iyenn.com/index/link?url=https://blog.csdn.net/laoyuanpython/category_9831699.html 专栏：Python基础教程目录）从零开始学习Python。

如果有兴趣也愿意支持老猿的读者，欢迎购买付费专栏。

跟老猿学Python！

☞ ░ 前往老猿Python博文目录 https://blog.csdn.net/LaoYuanPython ░

线性变换
同构
齐次函数

http://www.doc88.com/p-9913634445186.html
正定对称双线性
群论

http://www.doc88.com/p-9913634445186.html
正定对称双线性
群论

文章知识点与官方知识档案匹配，可进一步学习相关知识
Python入门技能树人工智能机器学习工具包Scikit-learn333560 人正在系统学习中
老猿Python
微信公众号
专注Python相关语言、图像音视频处理、AI
注：本文转载自blog.csdn.net的LaoYuanPython的文章"https://blog.csdn.net/LaoYuanPython/article/details/112460899"。版权归原作者所有，此博客不拥有其著作权，亦不承担相应法律责任。如有侵权，请联系我们删除。
复制链接
相关推荐
发表评论

评论记录：

未查询到任何数据！