引言

上一节介绍了波尔兹曼机，并对波尔兹曼机的对数似然梯度进行描述。本节将使用马尔可夫链蒙特卡洛方法对模型参数的梯度进行求解。

回顾：波尔兹曼机

波尔兹曼机的结构表示

这里讨论的含隐变量的波尔兹曼机。基于波尔兹曼机的概率图结构，可以将结点分成两个部分：

• 观测变量集合(Observed Variable)$v$：观测变量的特征是样本集合提供的，可观测的变量信息。
• 隐变量集合(Latent Variable)$h$：隐变量的特征是基于假定的概率图模型产生的特征。

无论是观测变量还是隐变量，在波尔兹曼机中均服从伯努利分布：
{ v = ( v 1 , v 2 , ⋯   , v D ) T ; v ∈ { 0 , 1 } D h = ( h 1 , h 2 , ⋯   , h P ) T ; h ∈ { 0 , 1 } P

$$\begin{cases} v = (v_1,v_2,\cdots,v_{\mathcal D})^T;v \in \{0,1\}^{\mathcal D} \\ h = (h_1,h_2,\cdots,h_{\mathcal P})^T;h \in \{0,1\}^{\mathcal P} \end{cases}$$ {v=(v1​,v2​,⋯,vD​)T;v∈{0,1}Dh=(h1​,h2​,⋯,hP​)T;h∈{0,1}P​
其中$\mathcal{D},\mathcal{P}$分别表示观测变量，隐变量集合中随机变量的数量，那么基于玻尔兹曼机的约束条件，可以将概率密度函数(联合概率分布)表示如下：
P ( X ; θ ) = P ( v , h ; θ ) = { 1 Z exp ⁡ { − E ( v , h ) } E ( v , h ) = − [ v T W ⋅ h + 1 2 v T L ⋅ v + 1 2 h T J ⋅ h ] \mathcal P(\mathcal X;\theta) = \mathcal P(v,h;\theta) = $$\begin{cases} \frac{1}{\mathcal Z} \exp \{ - \mathbb E(v,h)\} \\ \mathbb E(v,h) = - \left[v^T \mathcal W \cdot h + \frac{1}{2} v^T \mathcal L\cdot v + \frac{1}{2} h^T \mathcal J \cdot h\right] \end{cases}$$ P(X;θ)=P(v,h;θ)={Z1​exp{−E(v,h)}E(v,h)=−[vTW⋅h+21​vTL⋅v+21​hTJ⋅h]​
其中模型参数$\theta$由变量之间边的权重$\mathcal{W},\mathcal{L},\mathcal{J}$共同构成。其中：

• $\mathcal{W}$表示观测变量、隐变量之间边的权重组成的矩阵，其中${\mathcal{W}}_{ij}$表示第$i$个观测变量与第$j$个隐变量之间关系的权重信息。
  如果某观测变量与某隐变量之间不存在边相关联，那么对应的权重信息等于0.
  $$\mathcal{W}=[{\mathcal{W}}_{ij}{]}_{\mathcal{D}\times \mathcal{P}}={\left(\begin{array}{c}{\mathcal{W}}_{11},{\mathcal{W}}_{12},\cdots ,{\mathcal{W}}_{1\mathcal{P}}\\ {\mathcal{W}}_{21},{\mathcal{W}}_{22},\cdots ,{\mathcal{W}}_{2\mathcal{P}}\\ ⋮\\ {\mathcal{W}}_{\mathcal{D}1},{\mathcal{W}}_{\mathcal{D}2},\cdots ,{\mathcal{W}}_{\mathcal{DP}}\end{array}\right)}_{\mathcal{D}\times \mathcal{P}}$$
• 同理，$\mathcal{L},\mathcal{J}$分别表示观测变量、隐变量内部关系的权重信息。基于波尔兹曼机是一个无向图模型，因此对应的$\mathcal{L},\mathcal{J}$均是实对称矩阵，并且对角线上的元素均为0：
  主对角线上元素表示各结点和自身的关联信息。基于波尔兹曼机的条件，模型中的结点不会与自身存在边相连接。
  $$\begin{gathered} \mathcal{L}=[{\mathcal{L}}_{ij}{]}_{\mathcal{D}\times \mathcal{D}}={\left(\begin{array}{c}{\mathcal{L}}_{11}=0,{\mathcal{L}}_{12},\cdots ,{\mathcal{L}}_{1\mathcal{D}}\\ {\mathcal{L}}_{21},{\mathcal{L}}_{22}=0,\cdots ,{\mathcal{L}}_{2\mathcal{D}}\\ ⋮\\ {\mathcal{L}}_{\mathcal{D}1},{\mathcal{L}}_{\mathcal{D}2},\cdots ,{\mathcal{L}}_{\mathcal{DD}}=0\end{array}\right)}_{\mathcal{D}\times \mathcal{D}} \\ \mathcal{J}=[{\mathcal{J}}_{ij}{]}_{\mathcal{P}\times \mathcal{P}}={\left(\begin{array}{c}{\mathcal{J}}_{11}=0,{\mathcal{J}}_{12},\cdots ,{\mathcal{J}}_{1\mathcal{P}}\\ {\mathcal{J}}_{21},{\mathcal{J}}_{22}=0,\cdots ,{\mathcal{J}}_{2\mathcal{P}}\\ ⋮\\ {\mathcal{J}}_{\mathcal{P}1},{\mathcal{J}}_{\mathcal{P}2},\cdots ,{\mathcal{J}}_{\mathcal{PP}}=0\end{array}\right)}_{\mathcal{P}\times \mathcal{P}} \end{gathered}$$

模型参数的对数似然梯度

对于波尔兹曼机的模型参数求解(学习任务)问题，由于波尔兹曼机模型结构的复杂性，因而没有办法求解模型参数的解析解。因此，通常使用极大似然估计，通过求解模型参数的对数似然梯度，从而使用梯度上升法来逼近模型参数的最优解。

已知样本集合 V = { v ( 1 ) , v ( 2 ) , ⋯   , v ( N ) } ; v ( i ) ∈ { 0 , 1 } D \mathcal V = \{v^{(1)},v^{(2)},\cdots,v^{(N)}\};v^{(i)} \in \{0,1\}^{\mathcal D} V={v(1),v(2),⋯,v(N)};v(i)∈{0,1}D。因此，似然函数$\mathcal{P}(\mathcal{V};\theta )$可表示为如下形式：
P ( V ; θ ) = 1 N log ⁡ ∏ i = 1 N P ( v ( i ) ; θ ) = 1 N ∑ i = 1 N log ⁡ P ( v ( i ) ; θ ) θ = { W , L , J }

$$\begin{aligned} \mathcal P(\mathcal V;\theta) & = \frac{1}{N} \log \prod_{i=1}^N \mathcal P(v^{(i)};\theta) \\ & = \frac{1}{N} \sum_{i=1}^N \log \mathcal P(v^{(i)};\theta) \quad \theta = \{\mathcal W,\mathcal L,\mathcal J\} \end{aligned}$$ P(V;θ)​=N1​logi=1∏N​P(v(i);θ)=N1​i=1∑N​logP(v(i);θ)θ={W,L,J}​
至此，需要对模型参数求解梯度。关于上述三个模型参数$\mathcal{W},\mathcal{L},\mathcal{J}$的梯度分别表示如下：
从概率密度函数的表达可以看出，这里并没有将$\frac{1}{2}$加上去。但并不影响$\mathcal{L},\mathcal{J}$的梯度方向，原因在于学习率$\eta$同样需要设定，在设定的过程中已经将参数$\frac{1}{2}$包含在内了。
$$\begin{array}{r}{\nabla }_{\mathcal{W}}\left[\log \mathcal{P}(v^{(i)};\theta )\right]={\mathbb{E}}_{{\mathcal{P}}_{data}}\left[v^{(i)}(h^{(i)}{)}^T\right]-{\mathbb{E}}_{{\mathcal{P}}_{model}}\left[v^{(i)}(h^{(i)}{)}^T\right]\\ {\nabla }_{\mathcal{L}}\left[\log \mathcal{P}(v^{(i)};\theta )\right]={\mathbb{E}}_{{\mathcal{P}}_{data}}\left[v^{(i)}(v^{(i)}{)}^T\right]-{\mathbb{E}}_{{\mathcal{P}}_{model}}\left[v^{(i)}(v^{(i)}{)}^T\right]\\ {\nabla }_{\mathcal{J}}\left[\log \mathcal{P}(v^{(i)};\theta )\right]={\mathbb{E}}_{{\mathcal{P}}_{data}}\left[h^{(i)}(h^{(i)}{)}^T\right]-{\mathbb{E}}_{{\mathcal{P}}_{model}}\left[h^{(i)}(h^{(i)}{)}^T\right]\end{array}$$
其中${\mathcal{P}}_{data}$表示真实分布，该分布由两部分组成：
$${\mathcal{P}}_{data}\Rightarrow {\mathcal{P}}_{data}(v^{(i)}\in \mathcal{V})\cdot {\mathcal{P}}_{model}\left[h^{(i)}\mid v^{(i)}\right]$$
其原因是：这里以模型参数$\mathcal{W}$为例。
$\mathcal{P}(h^{(i)}\mid v^{(i)})$表示隐变量的后验概率，而隐变量仅存在于假定模型中，因而$\mathcal{P}(h^{(i)}\mid v^{(i)})$是模型的分布，记作${\mathcal{P}}_{model}\left[h^{(i)}\mid v^{(i)}\right]$.
$${\mathbb{E}}_{{\mathcal{P}}_{data}}\left[v^{(i)}(h^{(i)}{)}^T\right]\approx {\mathbb{E}}_{{\mathcal{P}}_{data}(v^{(i)}\in \mathcal{V})}\left\{{\mathbb{E}}_{\mathcal{P}(h^{(i)}\mid v^{(i)})}\left[v^{(i)}(h^{(i)}{)}^T\right]\right\}$$
而${\mathcal{P}}_{model}$表示假定模型的概率分布，它的概率分布具体是联合概率分布：
$${\mathcal{P}}_{model}\Rightarrow {\mathcal{P}}_{model}(h^{(i)},v^{(i)})$$

基于MCMC梯度求解过程存在的问题

此时，各个模型参数的对数似然梯度已经表示出来，可以使用梯度上升法去近似求解最优模型参数：
这里以模型参数$\mathcal{W}$为例。
W ( t + 1 ) ⇐ W ( t ) + η ∇ W [ log ⁡ P ( v ( i ) ; θ ) ] ⇐ W ( t ) + η { E P d a t a [ v ( i ) ( h ( i ) ) T ] − E P m o d e l [ v ( i ) ( h ( i ) ) T ] }

$$\begin{aligned} \mathcal W^{(t+1)} & \Leftarrow \mathcal W^{(t)} + \eta \nabla_{\mathcal W} \left[\log \mathcal P(v^{(i)};\theta)\right] \\ & \Leftarrow \mathcal W^{(t)} + \eta \left\{\mathbb E_{\mathcal P_{data}} \left[v^{(i)}(h^{(i)})^T\right] - \mathbb E_{\mathcal P_{model}} \left[v^{(i)}(h^{(i)})^T\right]\right\} \end{aligned}$$ W(t+1)​⇐W(t)+η∇W​[logP(v(i);θ)]⇐W(t)+η{EPdata​​[v(i)(h(i))T]−EPmodel​​[v(i)(h(i))T]}​
并且模型参数的梯度${\nabla }_{\mathcal{W}}\left[\log \mathcal{P}(v^{(i)};\theta )\right]$本身也是一个矩阵形式：
需要注意：上标中的$(i)$表示某一具体样本；下标中的$i$表示其中一个观测变量。例如$v_i^{(i)}$表示具体样本$v^{(i)}$的第$i$个观测变量。
$$\begin{array}{r}{\nabla }_{\mathcal{W}}\left[\log \mathcal{P}(v^{(i)};\theta )\right]={\left\{{\nabla }_{{\mathcal{W}}_{ij}}\left[\log \mathcal{P}(v^{(i)};\theta )\right]\right\}}_{\mathcal{D}\times \mathcal{P}}\\ {\nabla }_{{\mathcal{W}}_{ij}}\left[\log \mathcal{P}(v^{(i)};\theta )\right]={\mathbb{E}}_{{\mathcal{P}}_{data}}\left[v_i^{(i)}(h_j^{(i)}{)}^T\right]-{\mathbb{E}}_{{\mathcal{P}}_{model}}\left[v_i^{(i)}(h_j^{(i)}{)}^T\right]\end{array}$$
对应图像如下，${\nabla }_{{\mathcal{W}}_{ij}}\left[\log \mathcal{P}(v^{(i)};\theta )\right]$描述的是红色线权重对应的梯度方向。

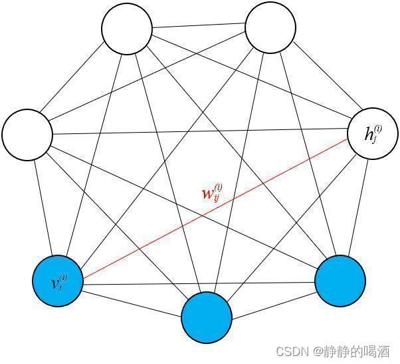
在配分函数——随机最大似然中介绍过，称${\mathbb{E}}_{{\mathcal{P}}_{data}}\left[v_i^{(i)}(h_j^{(i)}{)}^T\right]$为正相(Positive Phase)，称${\mathbb{E}}_{{\mathcal{P}}_{model}}\left[v_i^{(i)}(h_j^{(i)}{)}^T\right]$为负相(Negative Phase)。
但是波尔兹曼机中对于模型参数梯度的正相的特殊之处在于：$v_i^{(i)}(h_j^{(i)}{)}^T$中的$v_i^{(i)}$来自于真实样本分布${\mathcal{P}}_{data}(v^{(i)}\in \mathcal{V})$;而$h_j^{(i)}$来自于隐变量的后验分布${\mathcal{P}}_{model}(h^{(i)}\mid v^{(i)})$。
关于负相基于的分布是关于隐变量、观测变量的联合概率分布${\mathcal{P}}_{model}(h^{(i)},v^{(i)})$。
个人理解：

• 在上述的推导过程中，关于隐变量只能依赖于概率图模型的假设，使得隐变量不会凭空出现。
• 基于步骤1的描述，只要概率分布中含$h^{(i)}$,无论是条件概率还是联合概率分布，都不可能是‘真实分布’${\mathcal{P}}_{data}$。因为真实分布只能观察到‘观测变量’的信息。例如正相中的${\mathcal{P}}_{data}(v^{(i)}\in \mathcal{V})$;正相、负相均包含的${\mathcal{P}}_{model}(h^{(i)}\mid v^{(i)}),{\mathcal{P}}_{model}(h^{(i)},v^{(i)})$.

回顾受限玻尔兹曼机中对观测变量、隐变量之间关系的约束，可以直接将后验概率$\mathcal{P}(h\mid v)$求解出来：
P ( h ( i ) ∣ v ( i ) ) = ∏ j = 1 P P ( h j ( i ) ∣ v ( i ) ) P ( h j ( i ) ∣ v ( i ) ) = { Sigmoid ( ∑ i = 1 D W j i ( i ) v i ( i ) + c j ( i ) ) h j ( i ) = 1 1 − Sigmoid ( ∑ i = 1 D W j i ( i ) v i ( i ) + c j ( i ) ) h j ( i ) = 0

$$\begin{aligned} \mathcal P(h^{(i)} \mid v^{(i)}) & = \prod_{j=1}^{\mathcal P} \mathcal P(h_j^{(i)} \mid v^{(i)}) \\ \mathcal P(h_j^{(i)} \mid v^{(i)}) & = \begin{cases} \text{Sigmoid} \left(\sum_{i=1}^{\mathcal D} \mathcal W_{ji}^{(i)}v_i^{(i)} + c_j^{(i)}\right) \quad h_j^{(i)} = 1 \\ 1 - \text{Sigmoid} \left(\sum_{i=1}^{\mathcal D} \mathcal W_{ji}^{(i)}v_i^{(i)} + c_j^{(i)}\right) \quad h_j^{(i)} = 0 \\ \end{cases} \end{aligned}$$ P(h(i)∣v(i))P(hj(i)​∣v(i))​=j=1∏P​P(hj(i)​∣v(i))=⎩ ⎨ ⎧​Sigmoid(∑i=1D​Wji(i)​vi(i)​+cj(i)​)hj(i)​=11−Sigmoid(∑i=1D​Wji(i)​vi(i)​+cj(i)​)hj(i)​=0​​
此时的后验概率${\mathcal{P}}_{model}(h^{(i)}\mid v^{(i)})$可以直接使用观测变量进行表示，而${\mathcal{P}}_{data}(v^{(i)}\in \mathcal{V})$是基于样本集合$\mathcal{V}$产生的，因此关于受限波尔兹曼机的正相是可表示的。

但关于受限波尔兹曼机的负相部分，没有办法对联合概率分布直接进行求解，在受限波尔兹曼机——对数似然梯度求解过程中针对负相的积分问题，采用的是块吉布斯采样方法进行近似求解。由于受限波尔兹曼机中各隐变量之间相互独立，不需要传统采样方式中先固定除采样外的其他所有变量，再对该变量进行采样的方式，而是隐变量之间各采各的，互不影响。
为了增加采样效率，同样使用了对比散度的方式进行优化。

但如果将受限波尔兹曼机泛化至波尔兹曼机，此时由于没有隐变量/观测变量相互独立的约束，对于 ${\mathcal{P}}_{model}(h^{(i)}\mid v^{(i)})$同样没有办法进行求解。至此，无论是正相还是负相，波尔兹曼机都是极难直接求解的。

在当时给出的做法就是马尔可夫链蒙特卡洛方法(Markov Chain Monte Carlo,MCMC)，但是这种方式自然是非常棘手的。例如吉布斯采样，随着随机变量数量的增长，它的计算量是指数级别的增加。对于过多的随机变量，它的分布近似过程是十分复杂的。

例如，想要使用MCMC方法近似求解${\mathcal{P}}_{model}(h^{(i)}\mid v^{(i)})$，以上述的全连接波尔兹曼机为例，蓝色点给定的条件下，求解某一白色点的后验概率。这明显是不可求的——因为隐变量不仅仅和观测变量相关联，隐变量自身之间也存在关联，并且作为条件的观测变量之间也存在关联。如果使用因子图的方式对该模型进行分解——很遗憾，该概率图本身就是一个极大团，没有继续向下分解的可能。因而没有办法表示隐变量，并基于隐变量进行采样。

关于单个变量的后验概率

基于上面的介绍，可以知道：仅将观测变量作为条件，求解隐变量的后验概率${\mathcal{P}}_{model}(h^{(i)}\mid v^{(i)})$是基本不可能的。

能否退而求其次，通过单个变量(观测变量、隐变量)的后验概率去描述${\mathcal{P}}_{model}(h^{(i)}\mid v^{(i)}),{\mathcal{P}}_{model}(v^{(i)},h^{(i)})$呢？
这里单个变量的后验存在两种类型：
需要强调的点：无论$\mathcal{P}(v_i^{(i)}=1\mid h^{(i)},v_{-i}^{(i)})$还是$\mathcal{P}(h_j^{(i)}=1\mid v^{(i)},h_{-j}^{(i)})$,它们均只是某一个随机变量的后验概率，而不是隐变量/观测变量的后验概率。

• 某观测变量$v_i^{(i)}$的后验概率；
  $$\begin{array}{r}\mathcal{P}(v_i^{(i)}=1\mid h^{(i)},v_{-i}^{(i)})=\mathcal{P}(v_i^{(i)}=1\mid h_1^{(i)},\cdots ,h_{\mathcal{P}}^{(i)},v_1^{(i)},\cdots ,v_{i-1}^{(i)},v_{i+1}^{(i)},\cdots ,v_{\mathcal{D}}^{(i)})\end{array}$$
• 某隐变量$h_j^{(i)}$的后验概率；
  $$\mathcal{P}(h_j^{(i)}=1\mid v^{(i)},h_{-j}^{(i)})=\mathcal{P}(h_j^{(i)}=1\mid v_1^{(i)},\cdots ,v_{\mathcal{D}}^{(i)},h_1^{(i)},\cdots ,h_{j-1}^{(i)},h_{j+1}^{(i)},\cdots ,h_{\mathcal{P}}^{(i)})$$

这种表示方式给MCMC提供了有效的操作空间，例如吉布斯采样。假设对$v_i^{(i)}$进行采样的过程中，可以固定除$v_i^{(i)}$之外的所有随机变量。当$v_i^{(i)}$采样结束之后，再继续选择其他随机变量如$v_{i+1}^{(i)}$，再次执行上述操作。直到所有随机变量全部采样过，一次迭代才算结束，继续进行下一次迭代。最终达到平稳分布。
关于吉布斯采样，详见吉布斯采样——传送门

关于单个变量后验概率的推导过程

$\mathcal{P}(v_i^{(i)}\mid h^{(i)},v_{-i}^{(i)})$ 为例，描述它的推导过程。观察基于玻尔兹曼机条件下，该后验能够表示成什么形式：

• 使用条件概率公式，将$\mathcal{P}(v_i^{(i)}\mid h^{(i)},v_{-i}^{(i)})$表示为如下形式：
  $$\mathcal{P}(v_i^{(i)}\mid h^{(i)},v_{-i}^{(i)})=\frac{\mathcal{P}(h^{(i)},v_i^{(i)},v_{-i}^{(i)})}{\mathcal{P}(h^{(i)},v_{-i}^{(i)})}=\frac{\mathcal{P}(h^{(i)},v^{(i)})}{\mathcal{P}(h^{(i)},v_{-i}^{(i)})}$$
• 上式中分子部分明显是玻尔兹曼机的概率密度函数；而分母是概率密度函数将$v_i^{(i)}$积分掉后的结果。将概率密度函数带入，有：
  后续为了方便表达，将$\mathcal{P}(v_i^{(i)}\mid h^{(i)},v_{-i}^{(i)})$使用$\mathcal{I}$表示。
  I = P ( h ( i ) , v ( i ) ) ∑ v i ( i ) P ( h ( i ) , v ( i ) ) = 1 Z exp ⁡ { − E ( v ( i ) , h ( i ) ) } ∑ v i ( i ) 1 Z exp ⁡ { − E ( v ( i ) , h ( i ) ) } $$\begin{aligned} \mathcal I & = \frac{\mathcal P(h^{(i)},v^{(i)})}{\sum_{v_i^{(i)}} \mathcal P(h^{(i)},v^{(i)})} \\ & = \frac{\frac{1}{\mathcal Z}\exp \{ - \mathbb E(v^{(i)},h^{(i)})\}}{\sum_{v_i^{(i)}}\frac{1}{\mathcal Z}\exp \{ - \mathbb E(v^{(i)},h^{(i)})\}} \end{aligned}$$ I​=∑vi(i)​​P(h(i),v(i))P(h(i),v(i))​=∑vi(i)​​Z1​exp{−E(v(i),h(i))}Z1​exp{−E(v(i),h(i))}​​
  观察分布部分，$\mathcal{Z}$是配分函数，它的表示如下：
  Z = ∑ v ( i ) ∑ h ( i ) exp ⁡ { − E ( v ( i ) , h ( i ) ) } \mathcal Z = \sum_{v^{(i)}} \sum_{h^{(i)}} \exp \{- \mathbb E(v^{(i)},h^{(i)})\} Z=v(i)∑​h(i)∑​exp{−E(v(i),h(i))}
  可以看出，配分函数$\mathcal{Z}$与$v_i^{(i)}$之间没有关系，因此可以将$\frac{1}{\mathcal{Z}}$提到${\sum }_{v_i^{(i)}}$前面，最终和分子中的$\frac{1}{\mathcal{Z}}$消掉。然后根据 玻尔兹曼机的定义，将能量函数展开，最终表示如下：
  I = 1 Z exp ⁡ { − E ( v ( i ) , h ( i ) ) } 1 Z ∑ v i ( i ) exp ⁡ { − E ( v ( i ) , h ( i ) ) } = exp ⁡ { [ v ( i ) ] T W ⋅ h ( i ) + 1 2 [ v ( i ) ] T L ⋅ v ( i ) + 1 2 [ h ( i ) ] T J ⋅ h ( i ) } ∑ v i ( i ) exp ⁡ { [ v ( i ) ] T W ⋅ h ( i ) + 1 2 [ v ( i ) ] T L ⋅ v ( i ) + 1 2 [ h ( i ) ] T J ⋅ h ( i ) } $$\begin{aligned} \mathcal I & = \frac{\frac{1}{\mathcal Z} \exp \{- \mathbb E(v^{(i)},h^{(i)})\}}{\frac{1}{\mathcal Z}\sum_{v_i^{(i)}}\exp \{- \mathbb E(v^{(i)},h^{(i)})\}} \\ & = \frac{\exp \left\{[v^{(i)}]^T\mathcal W\cdot h^{(i)} + \frac{1}{2} [v^{(i)}]^T \mathcal L\cdot v^{(i)} +\frac{1}{2} [h^{(i)}]^T \mathcal J \cdot h^{(i)}\right\}}{\sum_{v_i^{(i)}}\exp \left\{[v^{(i)}]^T\mathcal W\cdot h^{(i)} + \frac{1}{2} [v^{(i)}]^T \mathcal L\cdot v^{(i)} +\frac{1}{2} [h^{(i)}]^T \mathcal J \cdot h^{(i)}\right\}} \end{aligned}$$ I​=Z1​∑vi(i)​​exp{−E(v(i),h(i))}Z1​exp{−E(v(i),h(i))}​=∑vi(i)​​exp{[v(i)]TW⋅h(i)+21​[v(i)]TL⋅v(i)+21​[h(i)]TJ⋅h(i)}exp{[v(i)]TW⋅h(i)+21​[v(i)]TL⋅v(i)+21​[h(i)]TJ⋅h(i)}​​
• 继续将分子分母的大括号展开：
  注意：$h^{(i)}$和${\sum }_{v_i^{(i)}}$之间没有关系，可以将分母中的$\frac{1}{2}[h^{(i)}{]}^T\mathcal{J}\cdot h^{(i)}$提到积分号前，并与分子中的对应项消掉。
  I = exp ⁡ { [ v ( i ) ] T W ⋅ h ( i ) + 1 2 [ v ( i ) ] T L ⋅ v ( i ) } ⋅ exp ⁡ { 1 2 [ h ( i ) ] T J ⋅ h ( i ) } exp ⁡ { 1 2 [ h ( i ) ] T J ⋅ h ( i ) } ⋅ ∑ v i ( i ) exp ⁡ { [ v ( i ) ] T W ⋅ h ( i ) + 1 2 [ v ( i ) ] T L ⋅ v ( i ) } = exp ⁡ { [ v ( i ) ] T W ⋅ h ( i ) + 1 2 [ v ( i ) ] T L ⋅ v ( i ) } ∑ v i ( i ) exp ⁡ { [ v ( i ) ] T W ⋅ h ( i ) + 1 2 [ v ( i ) ] T L ⋅ v ( i ) } $$\begin{aligned} \mathcal I & = \frac{\exp \left\{[v^{(i)}]^T\mathcal W \cdot h^{(i)} + \frac{1}{2} [v^{(i)}]^T \mathcal L \cdot v^{(i)}\right\} \cdot \exp\{\frac{1}{2} [h^{(i)}]^T \mathcal J \cdot h^{(i)}\}}{\exp \left\{\frac{1}{2} [h^{(i)}]^T \mathcal J \cdot h^{(i)}\right\} \cdot \sum_{v_i^{(i)}}\exp\left\{[v^{(i)}]^T\mathcal W \cdot h^{(i)} + \frac{1}{2} [v^{(i)}]^T \mathcal L \cdot v^{(i)}\right\}} \\ & = \frac{\exp\left\{[v^{(i)}]^T\mathcal W \cdot h^{(i)} + \frac{1}{2} [v^{(i)}]^T \mathcal L \cdot v^{(i)}\right\}}{\sum_{v_i^{(i)}}\exp\left\{[v^{(i)}]^T\mathcal W \cdot h^{(i)} + \frac{1}{2} [v^{(i)}]^T \mathcal L \cdot v^{(i)}\right\}} \end{aligned}$$ I​=exp{21​[h(i)]TJ⋅h(i)}⋅∑vi(i)​​exp{[v(i)]TW⋅h(i)+21​[v(i)]TL⋅v(i)}exp{[v(i)]TW⋅h(i)+21​[v(i)]TL⋅v(i)}⋅exp{21​[h(i)]TJ⋅h(i)}​=∑vi(i)​​exp{[v(i)]TW⋅h(i)+21​[v(i)]TL⋅v(i)}exp{[v(i)]TW⋅h(i)+21​[v(i)]TL⋅v(i)}​​
• 由于$v_i^{(i)}$服从伯努利分布，因而分母自然可以写成两项相加的形式$(v_i^{(i)}=0,v_i^{(i)}=1)$，并且在分母中$v_i^{(i)}$已经被积分掉，也就是说$v_i^{(i)}$在分母中不是变量。当$v_i^{(i)}=1$时，仅修改分子中的描述：
  $$\begin{array}{rl}\mathcal{P}(v_i^{(i)}=1\mid h^{(i)},v_{-i}^{(i)})& ={\mathcal{I}}_{v_i^{(i)}=1}\\ & =\frac{\exp \left\{[v^{(i)}{]}^T\mathcal{W}\cdot h^{(i)}+\frac{1}{2}[v^{(i)}{]}^T\mathcal{L}\cdot v^{(i)}\right\}{\mid }_{v_i^{(i)}=1}}{\exp \left\{[v^{(i)}{]}^T\mathcal{W}\cdot h^{(i)}+\frac{1}{2}[v^{(i)}{]}^T\mathcal{L}\cdot v^{(i)}\right\}{\mid }_{v_i^{(i)}=0}+\exp \left\{[v^{(i)}{]}^T\mathcal{W}\cdot h^{(i)}+\frac{1}{2}[v^{(i)}{]}^T\mathcal{L}\cdot v^{(i)}\right\}{\mid }_{v_i^{(i)}=1}}\end{array}$$
  定义符号：$\Delta =\exp \left\{[v^{(i)}{]}^T\mathcal{W}\cdot h^{(i)}+\frac{1}{2}[v^{(i)}{]}^T\mathcal{L}\cdot v^{(i)}\right\}$，上式可简写成如下形式：
  $$\mathcal{P}(v_i^{(i)}=1\mid h^{(i)},v_{-i}^{(i)})=\frac{{\Delta }_{v_i^{(i)}=1}}{{\Delta }_{v_i^{(i)}=0}+{\Delta }_{v_i^{(i)}=1}}$$
• 继续观察，暂时先不管$v_i^{(i)}$的取值，先观察$\Delta$。由于$\Delta$中全部是向量乘积的形式，因而将其展开，表示成连加形式：
  $$\begin{array}{rl}\Delta & =\exp \left\{[v^{(i)}{]}^T\mathcal{W}\cdot h^{(i)}+\frac{1}{2}[v^{(i)}{]}^T\mathcal{L}\cdot v^{(i)}\right\}\\ & =\exp \left\{\sum _{l=1}^{\mathcal{D}}\sum _{j=1}^{\mathcal{P}}{v}_l^{(i)}\cdot {\mathcal{W}}_{lj}\cdot h_j^{(i)}+\frac{1}{2}\sum _{l=1}^{\mathcal{D}}\sum _{k=1}^{\mathcal{D}}{v}_l^{(i)}\cdot {\mathcal{L}}_{lk}\cdot v_k^{(i)}\right\}\end{array}$$
  观察上式大括号中的第一项，${\sum }_{l=1}^{\mathcal{D}}{\sum }_{j=1}^{\mathcal{P}}{v}_l^{(i)}\cdot {\mathcal{W}}_{lj}\cdot h_j^{(i)}$内部一共包含$\mathcal{D}\times \mathcal{P}$个连加项，其中有$\mathcal{P}$个项是和$v_i^{(i)}$相关的：
  $$v_i^{(i)}\Rightarrow \sum _{j=1}^{\mathcal{P}}{v}_i^{(i)}\cdot {\mathcal{W}}_{ij}\cdot h_j^{(i)}$$
  同理，观察上式大括号中的第二项，$\frac{1}{2}{\sum }_{l=1}^{\mathcal{D}}{\sum }_{k=1}^{\mathcal{D}}{v}_l^{(i)}\cdot {\mathcal{L}}_{lk}\cdot v_k^{(i)}$内部一共包含$\mathcal{D}\times \mathcal{D}$个连加项，其中和$v_i^{(i)}$相关的项有$2\mathcal{D}-1$项：
  $\mathcal{L}$矩阵第$i$行与第$i$列的项之和。其中$i$行$i$列结果被加重了一次，需要减掉。
  $$v_i^{(i)}\Rightarrow \underset{1项}{\underbrace{v_i^{(i)}\cdot {\mathcal{L}}_{ii}\cdot v_i^{(i)}}}+\underset{\mathcal{D}-1项}{\underbrace{\sum _{l\ne i}^{\mathcal{D}}{v}_l^{(i)}\cdot {\mathcal{L}}_{li}\cdot v_i^{(i)}}}+\underset{\mathcal{D}-1项}{\underbrace{\sum _{k\ne i}^{\mathcal{D}}{v}_i^{(i)}\cdot {\mathcal{L}}_{ik}\cdot v_k^{(i)}}}$$
  实际上，由于$\mathcal{L}$是对角线上元素为0的实对称矩阵，因此，有：
  $$\begin{array}{r}\sum _{l\ne i}^{\mathcal{D}}{v}_l^{(i)}\cdot {\mathcal{L}}_{li}\cdot v_i^{(i)}=\sum _{k\ne i}^{\mathcal{D}}{v}_i^{(i)}\cdot {\mathcal{L}}_{ik}\cdot v_k^{(i)}\\ v_i^{(i)}\Rightarrow \underset{=0}{\underbrace{v_i^{(i)}\cdot {\mathcal{L}}_{ii}\cdot v_i^{(i)}}}+2\sum _{k\ne i}^{\mathcal{D}}{v}_i^{(i)}\cdot {\mathcal{L}}_{ik}\cdot v_k^{(i)}\end{array}$$
• 至此，已经将所有关于$v_i^{(i)}$的项全部找到。最终将$\Delta$中的所有连加项分成与$v_i^{(i)}$相关和不相关的两部分：
  $$\begin{array}{rl}\Delta & =\exp \left\{\sum _{l\ne i}^{\mathcal{D}}\sum _{j=1}^{\mathcal{P}}{v}_l^{(i)}\cdot {\mathcal{W}}_{lj}\cdot h_j^{(i)}+\sum _{j=1}^{\mathcal{P}}{v}_i^{(i)}\cdot {\mathcal{W}}_{ij}\cdot h_j^{(i)}+\frac{1}{2}\left[\sum _{l\ne i}^{\mathcal{D}}\sum _{k\ne i}^{\mathcal{D}}{v}_l^{(i)}\cdot {\mathcal{L}}_{lk}\cdot v_k^{(i)}+\underset{=0}{\underbrace{v_i^{(i)}\cdot {\mathcal{L}}_{ii}\cdot v_i^{(i)}}}+2\sum _{k\ne i}^{\mathcal{D}}{v}_i^{(i)}\cdot {\mathcal{L}}_{ik}\cdot v_k^{(i)}\right]\right\}\\ & =\exp \left\{\sum _{l\ne i}^{\mathcal{D}}\sum _{j=1}^{\mathcal{P}}{v}_l^{(i)}\cdot {\mathcal{W}}_{lj}\cdot h_j^{(i)}+\sum _{j=1}^{\mathcal{P}}{v}_i^{(i)}\cdot {\mathcal{W}}_{ij}\cdot h_j^{(i)}+\frac{1}{2}\sum _{l\ne i}^{\mathcal{D}}\sum _{k\ne i}^{\mathcal{D}}{v}_l^{(i)}\cdot {\mathcal{L}}_{lk}\cdot v_k^{(i)}+\sum _{k\ne i}^{\mathcal{D}}{v}_i^{(i)}\cdot {\mathcal{L}}_{ik}\cdot v_k^{(i)}\right\}\end{array}$$
  当$v_i^{(i)}=0$时，${\Delta }_{v_i^{(i)}=0}$具体表示为：
  $$\begin{array}{rl}{\Delta }_{v_i^{(i)}=0}& =\exp \left\{\sum _{l\ne i}^{\mathcal{D}}\sum _{j=1}^{\mathcal{P}}{v}_l^{(i)}\cdot {\mathcal{W}}_{lj}\cdot h_j^{(i)}+\underset{=0}{\underbrace{\sum _{j=1}^{\mathcal{P}}{v}_i^{(i)}\cdot {\mathcal{W}}_{ij}\cdot h_j^{(i)}}}+\frac{1}{2}\sum _{l\ne i}^{\mathcal{D}}\sum _{k\ne i}^{\mathcal{D}}{v}_l^{(i)}\cdot {\mathcal{L}}_{lk}\cdot v_k^{(i)}+\underset{=0}{\underbrace{\sum _{k\ne i}^{\mathcal{D}}{v}_i^{(i)}\cdot {\mathcal{L}}_{ik}\cdot v_k^{(i)}}}\right\}\\ & =\exp \left\{\sum _{l\ne i}^{\mathcal{D}}\sum _{j=1}^{\mathcal{P}}{v}_l^{(i)}\cdot {\mathcal{W}}_{lj}\cdot h_j^{(i)}+\frac{1}{2}\sum _{l\ne i}^{\mathcal{D}}\sum _{k\ne i}^{\mathcal{D}}{v}_l^{(i)}\cdot {\mathcal{L}}_{lk}\cdot v_k^{(i)}\right\}\end{array}$$
  对应的$v_i^{(i)}=1$时，${\Delta }_{v_i^{(i)}=1}$具体表示为：
  $${\Delta }_{v_i^{(i)}=1}=\exp \left\{\sum _{l\ne i}^{\mathcal{D}}\sum _{j=1}^{\mathcal{P}}{v}_l^{(i)}\cdot {\mathcal{W}}_{lj}\cdot h_j^{(i)}+\sum _{j=1}^{\mathcal{P}}{\mathcal{W}}_{ij}\cdot h_j^{(i)}+\frac{1}{2}\sum _{l\ne i}^{\mathcal{D}}\sum _{k\ne i}^{\mathcal{D}}{v}_l^{(i)}\cdot {\mathcal{L}}_{lk}\cdot v_k^{(i)}+\sum _{k\ne i}^{\mathcal{D}}{\mathcal{L}}_{ik}\cdot v_k^{(i)}\right\}$$
• 最终，将${\Delta }_{v_i^{(i)}=0},{\Delta }_{v_i^{(i)}=1}$带回$\mathcal{P}(v_i^{(i)}=1\mid h^{(i)},v_{-i}^{(i)})=\frac{{\Delta }_{v_i^{(i)}=1}}{{\Delta }_{v_i^{(i)}=0}+{\Delta }_{v_i^{(i)}=1}}$中，有：
  分子、分母同时除以$\exp \left\{{\sum }_{l\ne i}^{\mathcal{D}}{\sum }_{j=1}^{\mathcal{P}}{v}_l^{(i)}\cdot {\mathcal{W}}_{lj}\cdot h_j^{(i)}+\frac{1}{2}{\sum }_{l\ne i}^{\mathcal{D}}{\sum }_{k\ne i}^{\mathcal{D}}{v}_l^{(i)}\cdot {\mathcal{L}}_{lk}\cdot v_k^{(i)}\right\}$
  $$\mathcal{P}(v_i^{(i)}=1\mid h^{(i)},v_{-i}^{(i)})=\frac{\exp \left\{{\sum }_{j=1}^{\mathcal{P}}{\mathcal{W}}_{ij}\cdot h_j^{(i)}+{\sum }_{k\ne i}^{\mathcal{D}}{\mathcal{L}}_{ik}\cdot v_k^{(i)}\right\}}{1+\exp \left\{{\sum }_{j=1}^{\mathcal{P}}{\mathcal{W}}_{ij}\cdot h_j^{(i)}+{\sum }_{k\ne i}^{\mathcal{D}}{\mathcal{L}}_{ik}\cdot v_k^{(i)}\right\}}$$
  基于上式，分子、分母继续同时除以$\exp \left\{{\sum }_{j=1}^{\mathcal{P}}{\mathcal{W}}_{ij}\cdot h_j^{(i)}+{\sum }_{k\ne i}^{\mathcal{D}}{\mathcal{L}}_{ik}\cdot v_k^{(i)}\right\}$,有：
  $$\begin{array}{rl}\mathcal{P}(v_i^{(i)}=1\mid h^{(i)},v_{-i}^{(i)})& =\frac{1}{1+\frac{1}{\exp \left\{{\sum }_{j=1}^{\mathcal{P}}{\mathcal{W}}_{ij}\cdot h_j^{(i)}+{\sum }_{k\ne i}^{\mathcal{D}}{\mathcal{L}}_{ik}\cdot v_k^{(i)}\right\}}}\\ & =\frac{1}{1+\exp -\left\{{\sum }_{j=1}^{\mathcal{P}}{\mathcal{W}}_{ij}\cdot h_j^{(i)}+{\sum }_{k\ne i}^{\mathcal{D}}{\mathcal{L}}_{ik}\cdot v_k^{(i)}\right\}}\\ & =\text{Sigmoid}\left\{\sum _{j=1}^{\mathcal{P}}{\mathcal{W}}_{ij}\cdot h_j^{(i)}+\sum _{k\ne i}^{\mathcal{D}}{\mathcal{L}}_{ik}\cdot v_k^{(i)}\right\}\end{array}$$

至此，得证单个观测变量$v_i^{(i)}$的后验概率是可求的，同理，单个隐变量$h_j^{(i)}$的后验概率$\mathcal{P}(h_j^{(i)}=1\mid v^{(i)},h_{-j}^{(i)})$也是可求的，并且也是$\text{Sigmoid}$函数：
这里就不证明了~
$$\mathcal{P}(h_j^{(i)}=1\mid v^{(i)},h_{-j}^{(i)})=\text{Sigmoid}\left\{\sum _{i=1}^{\mathcal{D}}{\mathcal{W}}_{ij}\cdot v_i^{(i)}+\sum _{m\ne j}{\mathcal{J}}_{jm}\cdot h_m^{(i)}\right\}$$
至此，在MCMC方法迭代的过程中，可以求解对应的后验概率并进行采样。

单个变量后验概率与受限玻尔兹曼机

该采样方法对于受限波尔兹曼机同样适用。例如$\mathcal{P}(h_j^{(i)}=1\mid v^{(i)})$。由于受限波尔兹曼机的性质，给定观测变量后，$h_j^{(i)}$和 h − j ( i ) = { h 1 ( i ) , ⋯   , h j − 1 ( i ) , h j + 1 ( i ) , ⋯   , h P ( i ) } h_{-j}^{(i)} = \{h_1^{(i)},\cdots,h_{j-1}^{(i)},h_{j+1}^{(i)},\cdots,h_{\mathcal P}^{(i)}\} h−j(i)​={h1(i)​,⋯,hj−1(i)​,hj+1(i)​,⋯,hP(i)​}之间不存在关联关系，因而可改写成如下形式：
将上述后验概率公式代入。注意的点：受限波尔兹曼机中隐变量之间不存在关联关系，因而${\sum }_{m\ne j}{\mathcal{J}}_{jm}\cdot h_m^{(i)}$内部只有一项，就是隐变量与自身相关联的参数项，这里用$c_j^{(i)}$表示。
P ( h j ( i ) = 1 ∣ v ( i ) ) = P ( h j ( i ) = 1 ∣ v ( i ) , h − j ( i ) ) = Sigmoid { ∑ i = 1 D W i j ⋅ v i ( i ) + ∑ m ≠ j J j m ⋅ h m ( i ) } = Sigmoid { ∑ i = 1 D W i j ⋅ v i ( i ) + c j ( i ) }

$$\begin{aligned} P(h_j^{(i)} = 1 \mid v^{(i)}) & = P(h_j^{(i)} = 1 \mid v^{(i)},h_{-j}^{(i)}) \\ & = \text{Sigmoid}\left\{ \sum_{i=1}^{\mathcal D} \mathcal W_{ij} \cdot v_{i}^{(i)} + \sum_{m \neq j} \mathcal J_{jm} \cdot h_m^{(i)}\right\} \\ & = \text{Sigmoid}\left\{ \sum_{i=1}^{\mathcal D} \mathcal W_{ij} \cdot v_{i}^{(i)} + c_j^{(i)}\right\} \end{aligned}$$ P(hj(i)​=1∣v(i))​=P(hj(i)​=1∣v(i),h−j(i)​)=Sigmoid⎩ ⎨ ⎧​i=1∑D​Wij​⋅vi(i)​+m=j∑​Jjm​⋅hm(i)​⎭ ⎬ ⎫​=Sigmoid{i=1∑D​Wij​⋅vi(i)​+cj(i)​}​
这与受限波尔兹曼机——后验概率中推导的结果完全相同，这说明，基于波尔兹曼机关于单个变量的后验概率同样可以在受限波尔兹曼机中使用。

相关参考：
(系列二十八)波尔兹曼机3-基于MCMC的随机梯度上升
(系列二十八)波尔兹曼机-条件概率推导