MD5加密(2)：MD5代码实现详解

在上一篇文章MD5加密(1)：MD5基础知识和计算过程中，我简单地介绍了MD5的实现原理。但理论的目的是实践，所以这一篇文章就来分析一下MD5的C语言代码实现。

文章目录

1 代码分析

MD5算法在PPP拨号中用于实现 CHAP(Challenge Handshake Authentication Protocol)认证方式。在CHAP认证中，拨号服务器向拨号客户端发送一个随机的challenge字符串，然后拨号客户端使用预先共享的密钥和这个挑战字符串进行MD5哈希运算。然后，将哈希结果发送给拨号服务器。拨号服务器使用相同的密钥和challenge字符串进行MD5哈希运算，并将计算得到的哈希结果与客户端发送的结果进行比较。如果两者匹配，认证成功，连接双方被认为是合法的。

我们就来参考一下LwIP中MD5代码的实现，它位于/lwip/src/netif/ppp/polarssl/md5.c。

1.1 大小端转换

由于在网络传输中大端传输更常见，而在单片机中小端的CPU更常见，所以需要做大小端字节序的转化。在代码中就定义了大小端转化的宏定义：

#define GET_ULONG_LE(n,b,i)                             \
{                                                       \
    (n) = ( (unsigned long) (b)[(i)    ]       )        \
        | ( (unsigned long) (b)[(i) + 1] <<  8 )        \
        | ( (unsigned long) (b)[(i) + 2] << 16 )        \
        | ( (unsigned long) (b)[(i) + 3] << 24 );       \
}

#define PUT_ULONG_LE(n,b,i)                             \
{                                                       \
    (b)[(i)    ] = (unsigned char) ( (n)       );       \
    (b)[(i) + 1] = (unsigned char) ( (n) >>  8 );       \
    (b)[(i) + 2] = (unsigned char) ( (n) >> 16 );       \
    (b)[(i) + 3] = (unsigned char) ( (n) >> 24 );       \
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15

其中GET_ULONG_LE用于从一个字节数组b中提取四个字节，并将它们组合成一个32位的无符号长整型数n，采用小端字节序；PUT_ULONG_LE用于将一个32位的无符号长整型数n分解成四个字节，并按小端字节序存储到一个字节数组b中。

1.2 md5_starts

在开始md5计算之前，需要初始化一些参数，相当于init操作，函数如下：

typedef struct
{
    unsigned long total[2];     /*!< number of bytes processed  */
    unsigned long state[4];     /*!< intermediate digest state  */
    unsigned char buffer[64];   /*!< data block being processed */
}
md5_context;

void md5_starts( md5_context *ctx )
{
    ctx->total[0] = 0;
    ctx->total[1] = 0;

    ctx->state[0] = 0x67452301;
    ctx->state[1] = 0xEFCDAB89;
    ctx->state[2] = 0x98BADCFE;
    ctx->state[3] = 0x10325476;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18

（1）total
MD5是以block为单位进行处理的，一个block有512bit，即64字节。total字段用来追踪整个MD5过程中已经处理的字节数，以便在数据处理过程中准确地计算数据的位数。
（2）state
这里的state就是MD Buffer，有4个32位的buffer，它们的值是固定的。

1.3 md5_process

这是一个static的处理函数，用于每个block的计算，来看看代码：

static void md5_process( md5_context *ctx, const unsigned char data[64] )
{
    unsigned long X[16], A, B, C, D;
	/* 将输入的512bit字符串的每四个字节，都做一个大小端转换并保存到X[16]中 */
    GET_ULONG_LE( X[ 0], data,  0 );
    GET_ULONG_LE( X[ 1], data,  4 );
    GET_ULONG_LE( X[ 2], data,  8 );
    GET_ULONG_LE( X[ 3], data, 12 );
    GET_ULONG_LE( X[ 4], data, 16 );
    GET_ULONG_LE( X[ 5], data, 20 );
    GET_ULONG_LE( X[ 6], data, 24 );
    GET_ULONG_LE( X[ 7], data, 28 );
    GET_ULONG_LE( X[ 8], data, 32 );
    GET_ULONG_LE( X[ 9], data, 36 );
    GET_ULONG_LE( X[10], data, 40 );
    GET_ULONG_LE( X[11], data, 44 );
    GET_ULONG_LE( X[12], data, 48 );
    GET_ULONG_LE( X[13], data, 52 );
    GET_ULONG_LE( X[14], data, 56 );
    GET_ULONG_LE( X[15], data, 60 );

/* 用于在MD5四轮操作中的数据转换的宏定义 */
#define S(x,n) ((x << n) | ((x & 0xFFFFFFFF) >> (32 - n)))

#define P(a,b,c,d,k,s,t)                                \
{                                                       \
    a += F(b,c,d) + X[k] + t; a = S(a,s) + b;           \
}

    A = ctx->state[0];
    B = ctx->state[1];
    C = ctx->state[2];
    D = ctx->state[3];

/* 执行MD5的四轮操作 */
#define F(x,y,z) (z ^ (x & (y ^ z)))

    P( A, B, C, D,  0,  7, 0xD76AA478 );
    P( D, A, B, C,  1, 12, 0xE8C7B756 );
    P( C, D, A, B,  2, 17, 0x242070DB );
    P( B, C, D, A,  3, 22, 0xC1BDCEEE );
    P( A, B, C, D,  4,  7, 0xF57C0FAF );
    P( D, A, B, C,  5, 12, 0x4787C62A );
    P( C, D, A, B,  6, 17, 0xA8304613 );
    P( B, C, D, A,  7, 22, 0xFD469501 );
    P( A, B, C, D,  8,  7, 0x698098D8 );
    P( D, A, B, C,  9, 12, 0x8B44F7AF );
    P( C, D, A, B, 10, 17, 0xFFFF5BB1 );
    P( B, C, D, A, 11, 22, 0x895CD7BE );
    P( A, B, C, D, 12,  7, 0x6B901122 );
    P( D, A, B, C, 13, 12, 0xFD987193 );
    P( C, D, A, B, 14, 17, 0xA679438E );
    P( B, C, D, A, 15, 22, 0x49B40821 );

#undef F

#define F(x,y,z) (y ^ (z & (x ^ y)))

    P( A, B, C, D,  1,  5, 0xF61E2562 );
    P( D, A, B, C,  6,  9, 0xC040B340 );
    P( C, D, A, B, 11, 14, 0x265E5A51 );
    P( B, C, D, A,  0, 20, 0xE9B6C7AA );
    P( A, B, C, D,  5,  5, 0xD62F105D );
    P( D, A, B, C, 10,  9, 0x02441453 );
    P( C, D, A, B, 15, 14, 0xD8A1E681 );
    P( B, C, D, A,  4, 20, 0xE7D3FBC8 );
    P( A, B, C, D,  9,  5, 0x21E1CDE6 );
    P( D, A, B, C, 14,  9, 0xC33707D6 );
    P( C, D, A, B,  3, 14, 0xF4D50D87 );
    P( B, C, D, A,  8, 20, 0x455A14ED );
    P( A, B, C, D, 13,  5, 0xA9E3E905 );
    P( D, A, B, C,  2,  9, 0xFCEFA3F8 );
    P( C, D, A, B,  7, 14, 0x676F02D9 );
    P( B, C, D, A, 12, 20, 0x8D2A4C8A );

#undef F
    
#define F(x,y,z) (x ^ y ^ z)

    P( A, B, C, D,  5,  4, 0xFFFA3942 );
    P( D, A, B, C,  8, 11, 0x8771F681 );
    P( C, D, A, B, 11, 16, 0x6D9D6122 );
    P( B, C, D, A, 14, 23, 0xFDE5380C );
    P( A, B, C, D,  1,  4, 0xA4BEEA44 );
    P( D, A, B, C,  4, 11, 0x4BDECFA9 );
    P( C, D, A, B,  7, 16, 0xF6BB4B60 );
    P( B, C, D, A, 10, 23, 0xBEBFBC70 );
    P( A, B, C, D, 13,  4, 0x289B7EC6 );
    P( D, A, B, C,  0, 11, 0xEAA127FA );
    P( C, D, A, B,  3, 16, 0xD4EF3085 );
    P( B, C, D, A,  6, 23, 0x04881D05 );
    P( A, B, C, D,  9,  4, 0xD9D4D039 );
    P( D, A, B, C, 12, 11, 0xE6DB99E5 );
    P( C, D, A, B, 15, 16, 0x1FA27CF8 );
    P( B, C, D, A,  2, 23, 0xC4AC5665 );

#undef F

#define F(x,y,z) (y ^ (x | ~z))

    P( A, B, C, D,  0,  6, 0xF4292244 );
    P( D, A, B, C,  7, 10, 0x432AFF97 );
    P( C, D, A, B, 14, 15, 0xAB9423A7 );
    P( B, C, D, A,  5, 21, 0xFC93A039 );
    P( A, B, C, D, 12,  6, 0x655B59C3 );
    P( D, A, B, C,  3, 10, 0x8F0CCC92 );
    P( C, D, A, B, 10, 15, 0xFFEFF47D );
    P( B, C, D, A,  1, 21, 0x85845DD1 );
    P( A, B, C, D,  8,  6, 0x6FA87E4F );
    P( D, A, B, C, 15, 10, 0xFE2CE6E0 );
    P( C, D, A, B,  6, 15, 0xA3014314 );
    P( B, C, D, A, 13, 21, 0x4E0811A1 );
    P( A, B, C, D,  4,  6, 0xF7537E82 );
    P( D, A, B, C, 11, 10, 0xBD3AF235 );
    P( C, D, A, B,  2, 15, 0x2AD7D2BB );
    P( B, C, D, A,  9, 21, 0xEB86D391 );

#undef F

    ctx->state[0] += A;
    ctx->state[1] += B;
    ctx->state[2] += C;
    ctx->state[3] += D;
}


  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59
  • 60
  • 61
  • 62
  • 63
  • 64
  • 65
  • 66
  • 67
  • 68
  • 69
  • 70
  • 71
  • 72
  • 73
  • 74
  • 75
  • 76
  • 77
  • 78
  • 79
  • 80
  • 81
  • 82
  • 83
  • 84
  • 85
  • 86
  • 87
  • 88
  • 89
  • 90
  • 91
  • 92
  • 93
  • 94
  • 95
  • 96
  • 97
  • 98
  • 99
  • 100
  • 101
  • 102
  • 103
  • 104
  • 105
  • 106
  • 107
  • 108
  • 109
  • 110
  • 111
  • 112
  • 113
  • 114
  • 115
  • 116
  • 117
  • 118
  • 119
  • 120
  • 121
  • 122
  • 123
  • 124
  • 125

首先，在上一篇文章中，我们知道MD5每个block需要经过四轮非线性的操作，公式如下：
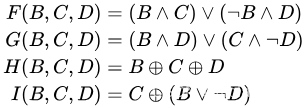
在这里插入图片描述
这是标准的MD5的四轮非线性的操作公式，但是可以发现在上述的代码中，前两轮的的公式与定义并不相同。这可能是因为MD5算法存在一些变种和改进版本，它们可能使用不同的四轮函数来满足特定的需求或目标。

由于每一轮就是这个非线性的操作公式不同，我们就以第一轮计算为例进行分析，其它三轮的处理类似。来看一下：

#define S(x,n) ((x << n) | ((x & 0xFFFFFFFF) >> (32 - n)))

#define P(a,b,c,d,k,s,t)                                \
{                                                       \
    a += F(b,c,d) + X[k] + t; a = S(a,s) + b;           \
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6

来回顾以下上一节的MD5流程：

  • 将B、C和D传递给一个非线性的计算过程，将得到的结果与A的值相加；对应：a += F(b,c,d)
  • 将子块的值添加到上述结果中；对应a += X[k]，每个子块占4字节，共16个子块
  • 添加本次迭代特定的常量值T[k]；对应a += t，这个常量可以自行指定
  • 对字符串进行循环移位；对应a += S(x,n)
  • 最后，将B的值添加到字符串中，并存储在缓冲区A中；对应a += b

这些步骤就对应了上面的宏定义P(a,b,c,d,k,s,t)。这里主要来看一下这个移位操作的宏定义S(x,n)。对于第一轮来说，移位的位数固定是7，12，17和22；第二轮是5，9，14和20；第三轮是4，11，16和23；第四轮是6，10，15，21。在md5的specification中有下面一句话：

The shift amounts in each round have been approximately optimized, to yield a faster “avalanche effect.” The shifts in different rounds are distinct.

也就是说，这些移位值是被测试过的，很容易引起“雪崩效应”，即字符串的一个很小的改动也能造成md5结果的很大的变化。另外，对于这个常量T来说，也是md5规范中规定的。具体为什么这么规定，涉及密码学的一些知识，这里不做深入的研究。

接着这个函数就是定义四个不同的非线性计算过程，经过四轮计算后得到A、B、C和D，最后将结果保存在ctx->state[4]中。

1.4 md5_update

这个函数是给用户调用的，可以多次调用md5_update一段一段地传入待求md5的字符串。但我们知道md5的计算是以512bit为单位的，不足512bit的话需要对字符串进行填充，所以这个函数会做一些填充操作，最后调用md5_process处理。如果数据长度不够就先保存在这，等待下一次md5_update或后面的md5_finish的调用。下面来看一下这个函数的实现：

void md5_update( md5_context *ctx, const unsigned char *input, int ilen )
{
    int fill;
    unsigned long left;

    if( ilen <= 0 )
        return;
	/* md5_process一次处理64字节,计算一下还需要多少字节能做一次处理 */
    left = ctx->total[0] & 0x3F;     //之前调用函数未处理完的字节数
    fill = 64 - left;                //还需填充的字节数
	/* 更新已处理的字节数 */
    ctx->total[0] += ilen;
    /* 确保总字节数不超过32位 */
    ctx->total[0] &= 0xFFFFFFFF;
	/* 如果低32位溢出,则增加高32位的值,实际上就是在32位机上操作一个64位的值 */
    if( ctx->total[0] < (unsigned long) ilen )
        ctx->total[1]++;
	/* 如果上次有剩字节没处理完且加上本次的数据后长度达到64字节,就处理这个块 */
    if( left && ilen >= fill )
    {
    	/* 将需要的组成一个block字节数的输入复制到buffer中 */
        MEMCPY( (void *) (ctx->buffer + left),
                input, fill );
        /* 计算MD5 */
        md5_process( ctx, ctx->buffer );
        /* 移动input的指针 */
        input += fill;
        /* 将长度减去此次已经计算的字节数 */
        ilen  -= fill;
        /* 没有剩余的字节数 */
        left = 0;
    }
	/* 如果此时输入的字节数还大于64,则继续进行md5计算,直到字节数小于64 */
    while( ilen >= 64 )
    {
        md5_process( ctx, input );
        input += 64;
        ilen  -= 64;
    }
	/* 将不足64的字节保存起来，待后续字节输入满了64字节后再计算 */
    if( ilen > 0 )
    {
        MEMCPY( (void *) (ctx->buffer + left),
                input, ilen );
    }
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46

函数的具体流程都写在注释中了，实际上就是每64字节组成一个block后，就计算一次MD5。

1.5 md5_finish

当用户所有的字符都输入后，调用此函数即可得到md5的结果。我们有提到一定要满64字节才能进行一次计算，那要是整个字符串的长度不是64的倍数呢？这就需要我们手动补齐了。在上一节中也有提到，在输入字符串的末尾添加一个"1"，然后再用"0"填充剩余的位数，最后还要预留64位，用来指示MD5输入字符串的长度。

static const unsigned char md5_padding[64] =
{
 0x80, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
    0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
    0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
    0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0
};

void md5_finish( md5_context *ctx, unsigned char output[16] )
{
    unsigned long last, padn;
    unsigned long high, low;
    unsigned char msglen[8];
	/* 最后8字节用于保存此次MD5的位数 */
    high = ( ctx->total[0] >> 29 )
         | ( ctx->total[1] <<  3 );
    low  = ( ctx->total[0] <<  3 );
	/* 需要小端保存 */
    PUT_ULONG_LE( low,  msglen, 0 );
    PUT_ULONG_LE( high, msglen, 4 );
	/* 看一下还剩多少字节没有计算MD5,做最后的填充 */
    last = ctx->total[0] & 0x3F;
    padn = ( last < 56 ) ? ( 56 - last ) : ( 120 - last );
	/* 计算剩余的没计算的位、padding的1/0和length的MD5 */
    md5_update( ctx, md5_padding, padn );
    md5_update( ctx, msglen, 8 );
	/* 结果保存在ctx->state中,也是小端保存 */
    PUT_ULONG_LE( ctx->state[0], output,  0 );
    PUT_ULONG_LE( ctx->state[1], output,  4 );
    PUT_ULONG_LE( ctx->state[2], output,  8 );
    PUT_ULONG_LE( ctx->state[3], output, 12 );
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32

上面的代码有两个地方详细说明一下：
（1）最后8字节长度的移位操作？

high = ( ctx->total[0] >> 29 ) | ( ctx->total[1] <<  3 );
low  = ( ctx->total[0] <<  3 );

  • 1
  • 2

这两行代码可以理解为对将64位的数左移三位，也就是乘以8。这是因为这个长度是以bit为单位的，而我们前面计算的长度total是以字节为单位的。也就是说实际上MD5最多支持长度为 2 61 2^{61} 261字节的数据，当然这个数已经非常大了。

（2）剩余字节的填充？

last = ctx->total[0] & 0x3F;
padn = ( last < 56 ) ? ( 56 - last ) : ( 120 - last );

  • 1
  • 2

如果小于56，则填充md5_padding到56字节，因为最后还有8字节的md5 length要添加组成一个block。如果大于等于56，则要多加一个block，将length写在下一个block中，填充的长度为(64-last+64-8) = (120-last)，其中last>=56，所以填充的长度不会超过64，故md5_padding数组的长度为64。

  • 从代码中可以看出：输入字符串的末尾添加一个"1"是必须的，而后面的“0”在字符串长度正好满足的情况下，可以不填

2 总结

MD5是一种哈希算法，用于将任意长度的数据转换为固定长度的哈希值。通过将数据映射到唯一的哈希值，MD5可以用于验证数据的完整性、生成数字签名、加密密码等应用。虽然MD5是一个经典的哈希函数，但由于其已经被证明存在安全弱点，现代安全需求更倾向于使用更强大的哈希算法，如SHA-256、AES。因此，在实际应用中，如果安全性是关键考量因素，我们不应该直接使用MD5，而是选择更安全的哈希算法。

特别是AES，我写的每一个BootLoader程序中都有使用到AES加解密，对于一些高端的单片机，如NXP的I.MX RT1176，它还在硬件上实现了一个OTFAD，用来实时进行AES解密运行程序。所以后续我打算写文章深入了解一下AES算法，来看看它里面是怎么实现的。

注：本文转载自blog.csdn.net的tilblackout的文章"https://blog.csdn.net/tilblackout/article/details/131880372"。版权归原作者所有，此博客不拥有其著作权，亦不承担相应法律责任。如有侵权，请联系我们删除。
复制链接
相关推荐
发表评论

评论记录：

未查询到任何数据！