转载请说明出处：http://blog.csdn.net/zhubaohua_bupt/article/details/74973347

在VSLAM优化部分，我们多次谈到，构建一个关于待优化位姿的误差函数

（直接法：灰度误差  ；特征点法：重投影误差），

当待优化的位姿使这个误差函数最小时(当SLAM运动不是太剧烈时，误差函数满足单峰性)，认为此时位姿最精确。

如果这个误差函数是线性，而且已知解析式的，很容易通过求导，令导数=0,求极值解决问题。

然而，误差函数是关于待优化位姿的一个非线性多元函数，怎么求使这个误差函数最小的位姿呢？

实际上，这是一个非线性无约束最优化问题，在目前主流的VSLAM(比如ORB，SVO，LSD)里，

采用的优化算法主要有两种：

一种是高斯牛顿(Gauss Newton)算法，另一种是列文伯格-马夸尔特(Levenberg-Marquardt)算法，简称LM算法。

下面我们详细探讨一下，高斯牛顿和LM算法的原理以及在VSLAM中的应用。

首先，最小二乘是要解决什么问题？

       1 最小二乘算法

     1.1 线性最小二乘问题

             

1.2 非线性最小二乘问题

               

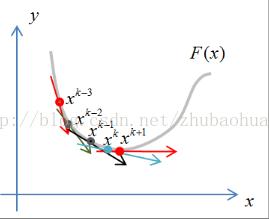
迭代过程如下图所示：

1.2.1 高斯牛顿法

               

1.2.2 LM算法

     http://iyenn.com/rec/746064.html