引言

上一节介绍了随机梯度下降$(\text{Stochastic Gradient Descent,SGD})$，本节将介绍动量法。

回顾：条件数与随机梯度下降的相应缺陷

早在梯度下降法在强凸函数的收敛性分析中介绍了条件数$(\text{Condition Number})$的概念。如果目标函数$f(\cdot )$在某点处的$\text{Hessian Matrix}\Rightarrow {\nabla }^{2}f(\cdot )$存在并且它具备：
这意味着$\text{Hessian Matrix}$必然是正定矩阵。
$${\nabla }^{2}f(\cdot )\succcurlyeq \mathcal{I}$$
那么它的条件数$\mathcal{C}$可表示为：
$$\mathcal{C}=\frac{{\lambda }_{max}}{{\lambda }_{min}}$$
其中${\lambda }_{max}$与${\lambda }_{min}$分别表示${\nabla }^{2}f(\cdot )$特征值的最大、最小值。如果$\mathcal{C}$过大，会导致：使用梯度下降法处理$f(\cdot )$的优化问题，当$\mathcal{C}\Rightarrow \infty$时，那么算法的收敛速度由线性收敛退化至次线性收敛。这种现象也被称作$\text{Hessain Matrix}$的病态条件。

上面仅仅是理论上的描述。在真实环境下，会出现什么样的效果$?$以标准二次型$f(x)=x^T\mathcal{Q}x$为例，其中 Q = ( 0.5 0 0 20 ) , x = ( x 1 , x 2 ) T \mathcal Q = (0.50020)

• 由于$\mathcal{Q}$是对角阵，因而它的特征值分别是$0.5,20$因而在$f(x)$定义域内的点，其对应$\text{Hessian Matrix}$的条件数也是不低的。
• 如果从目标函数的角度观察，它会是一个中间狭窄，两端狭长的船形形状。
• 关于该图代码见文章末尾,下同~
  

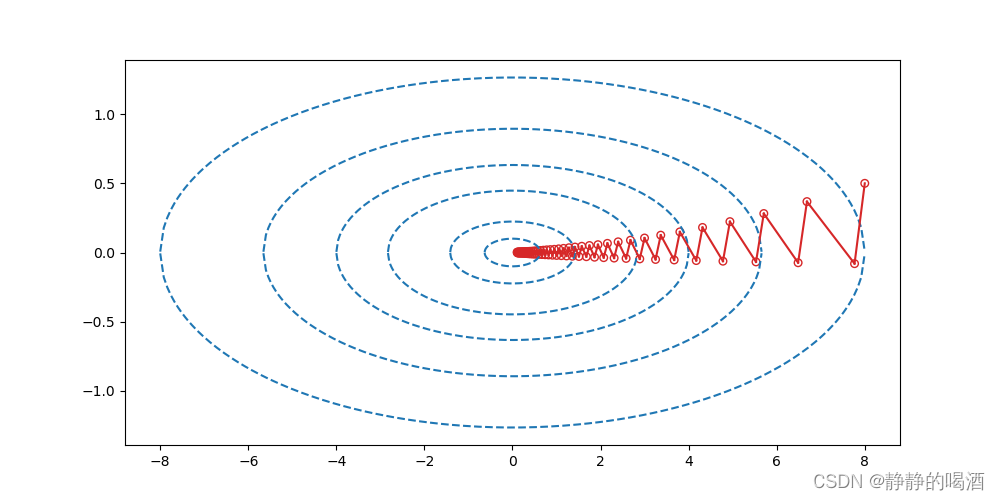
在该示例中，我们并不否认其最终收敛到最优解，但使用迭代步骤的数量是比较夸张的：

• 其中一个原因是梯度下降法不具备二次终止性——即便已经到达最优解附近，但依然不能基于有限迭代步骤内接近最优解；
• 在整个迭代过程中，梯度下降法在$f(\cdot )$的收敛路径过于冗余(线性收敛退化至次线性收敛的效果)——完全可以通过震荡更小的、路径更直接的方式实现收敛过程。

动量法简单认识

关于上述梯度下降法的迭代公式表示如下：
$$\theta \Leftarrow \theta -\eta \cdot {\nabla }_{\theta }\mathcal{J}(\theta )$$
其中$\eta$表示学习率。它可以被理解为每一迭代步骤，负梯度方向上调整的步长大小。随着迭代步骤的推移，梯度结果逐渐减小，而学习率是固定值，从而导致收敛速度越来越慢：

• 如果目标函数$f(\cdot )$至少是严格凸函数，那么$f(\cdot )$存在全局解，这种情况充其量是不具备二次终止性——需要花费较长时间收敛到最优解附近；
• 但如果目标函数非常复杂，收敛速度慢可能导致：数值解陷入局部最优或者鞍点。

关于动量法的迭代公式表示如下：
一些文章中也描述为: { m ⇐ γ ⋅ m + η ⋅ ∇ θ J ( θ ) θ ⇐ θ − m {m⇐γ⋅m+η⋅∇θJ(θ)θ⇐θ−m

而动量法的核心思想是：利用过去累积的梯度元素与当前迭代步骤的梯度元素进行加权运算，使其朝着最优解更快收敛：

• 如果$\gamma =0$意味着：在当前迭代步骤中，之前累积的梯度元素没有任何比重。也就是说，每次迭代过程仅与当前迭代步骤的梯度相关，此时的动量法也退化为梯度下降法。这里以$\gamma =0.1$图像进行示例：
  其中绿色图像表示梯度下降法的迭代路径;红色图像则表示$\gamma =0.1$时动量法的迭代路径。此时两者已经非常接近了，但动量法的迭代步骤明显小于梯度法。
  
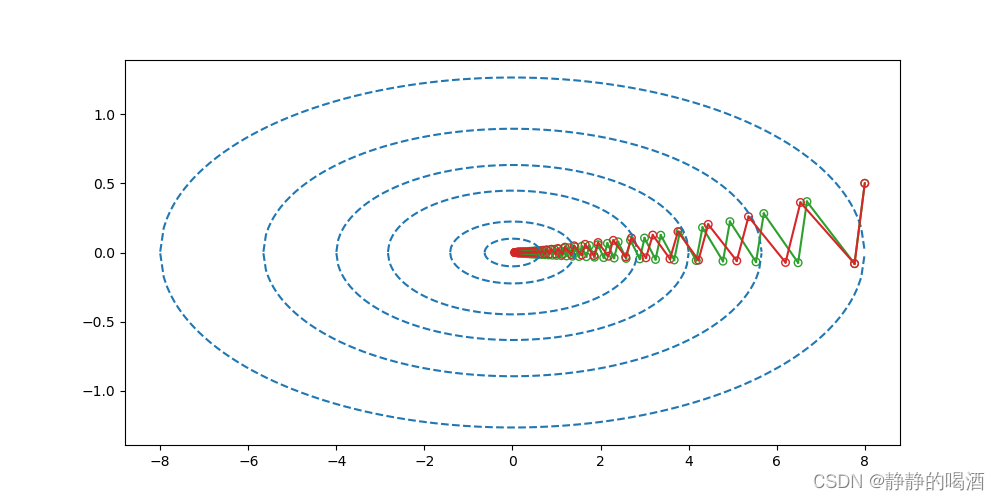
• 如果$\gamma \Rightarrow 1$意味着：当前迭代步骤中的梯度信息几乎不起作用，而过去累积的梯度元素占主导部分。这里以$\gamma =0.9$为例，对应图像结果表示如下：
  很明显，通过红色图像可知，当前迭代步骤的梯度元素也是有意义的，不能过于否定当前结果而过于依赖过去信息。
  
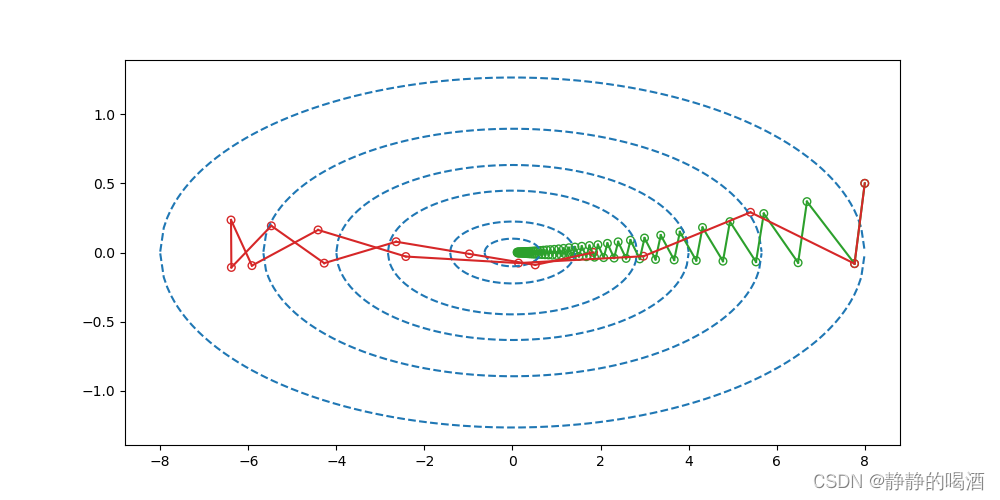
• 因而需要找到合适的$\gamma$，使其能够稳定收敛的基础上，减少迭代路径的距离。例如$\gamma =0.6$时的图像结果：
  可以明显看出:随着迭代步骤的更新，动量法迭代的幅度(跨越的距离长度)越来越大。即:过去梯度元素牵制着当前步骤的梯度方向。从而会有效减少更新步骤。并且，对于这类病态条件的二次目标函数有着不错的效果。
  

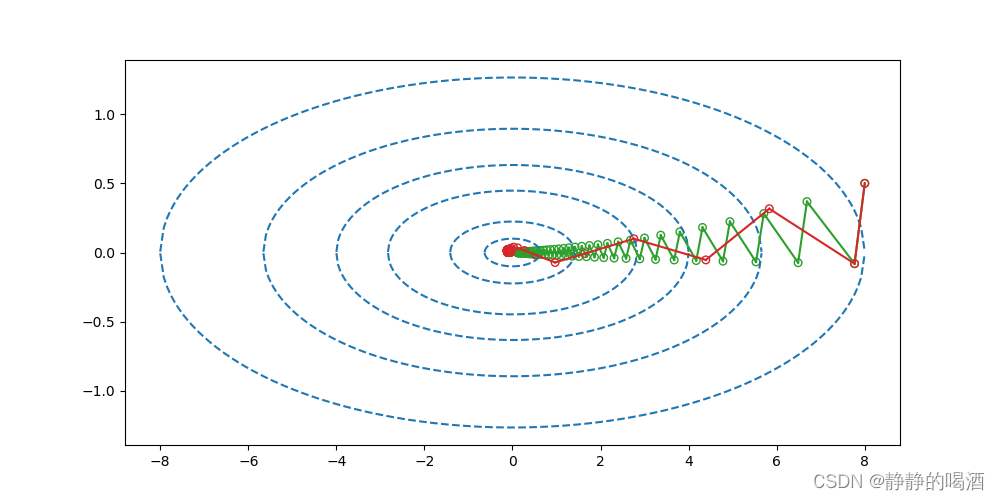
关于动量法的更新速度，见如下示例：

• $m_t$表示第$t$次迭代步骤的动量；假设每次迭代的梯度结果均相同，为$\mathcal{G}={\nabla }_{\theta }\mathcal{J}(\theta )$，从初始时刻$m_0=0$开始，有如下迭代过程：
  常用泰勒公式，需要满足$\gamma \in (-1,1)$
  $$\begin{gathered} m_0=0 \\ {m}_1=\gamma \cdot m_0+\eta \cdot \mathcal{G}=\eta \cdot \mathcal{G} \\ {m}_2=\gamma \cdot m_1+\eta \cdot \mathcal{G}=(1+\gamma )\eta \cdot \mathcal{G} \\ {m}_3=\gamma \cdot m_2+\eta \cdot \mathcal{G}=(1+\gamma +{\gamma }^2)\eta \cdot \mathcal{G} \\ ⋮ \\ {m}_{+\infty }=(1+\gamma +{\gamma }^2+{\gamma }^3+\cdots )\eta \cdot \mathcal{G}=\frac{1}{1-\gamma }\eta \cdot \mathcal{G} \end{gathered}$$
• 这意味着：动量在迭代过程中进行累积，$\gamma$越大，动量越大，它的迭代幅度越大，更新速度也更快(见上图$2$)。反之，一直快下去也不是优质的选择，我们同样需要当前迭代步骤的$\eta \cdot \mathcal{G}$对动量进行约束。

动量法的算法过程描述

基于动量法的随机梯度下降的算法步骤表示如下：
初始化操作：

• 学习率$\eta$，动量因子$\gamma$；
• 初始化参数$\theta$，初始动量$m$；

算法过程：

• $\text{While}$ 没有达到停止准则 $\text{do}$
• 从训练集$\mathcal{D}$中采集出 包含$k$个样本的小批量：$\{(x^{(i)},y^{(i)}){\}}_{i=1}^k$；
• 计算当前迭代步骤的梯度估计：
  其中$f(x^{(i)};\theta )$表示模型预测结果;$\mathcal{L}(\cdot )$表示损失函数;
  $$\mathcal{G}=\frac{1}{k}\sum _{i=1}^k{\nabla }_{\theta }\mathcal{L}[f(x^{(i)};\theta ),y^{(i)}]$$
• 计算动量更新：
  $$m\Leftarrow \gamma \cdot m-\eta \cdot \mathcal{G}$$
• 计算参数$\theta$更新：
  $$\theta \Leftarrow \theta +m$$
• $\text{End While}$

附：动量法示例代码

注：代码中没有使用确定的学习率作为步长，是对最速下降法代码的一个修改，使用查找的方式找到一个优质步长实现迭代过程。

import numpy as np
import math
import matplotlib.pyplot as plt

def f(x, y):
    return 0.5 * (x ** 2) + 20 * (y ** 2)

def ConTourFunction(x, Contour):
    return math.sqrt(0.05 * (Contour - (0.5 * (x ** 2))))

def Derfx(x):
    return x

def Derfy(y):
    return 40 * y

def DrawBackGround():
    ContourList = [0.2, 1.0, 4.0, 8.0, 16.0, 32.0]
    LimitParameter = 0.0001
    plt.figure(figsize=(10, 5))
    for Contour in ContourList:
        # 设置范围时，需要满足x的定义域描述。
        x = np.linspace(-1 * math.sqrt(2 * Contour) + LimitParameter, math.sqrt(2 * Contour) - LimitParameter, 200)
        y1 = [ConTourFunction(i, Contour) for i in x]
        y2 = [-1 * j for j in y1]
        plt.plot(x, y1, '--', c="tab:blue")
        plt.plot(x, y2, '--', c="tab:blue")

def GradientDescent(stepTime=80,epsilon=5.0,mode="momentum"):

    assert mode in ["SGD","momentum"]
    Start = (8.0, 0.5)
    StartV = (0.0, 0.0)
    alpha = 0.6
    LocList = list()
    LocList.append(Start)
    
    for _ in range(stepTime):
    
        DerStart = (Derfx(Start[0]), Derfy(Start[1]))
        for _,step in enumerate(list(np.linspace(0.0, 1.0, 1000))):

            if mode == "momentum":
                NextV = (alpha * StartV[0] - step * DerStart[0], alpha * StartV[1] - step * DerStart[1])
                Next = (Start[0] + NextV[0],Start[1] + NextV[1])
                DerfNext = Derfx(Next[0]) * (-1 * DerStart[0]) + Derfy(Next[1]) * (-1 * DerStart[1])

                if abs(DerfNext) <= epsilon:
                    LocList.append(Next)
                    StartV = NextV
                    Start = Next
                    epsilon /= 1.1
                    break
            else:
                Next = (Start[0] - (DerStart[0] * step), Start[1] - (DerStart[1] * step))
                DerfNext = Derfx(Next[0]) * (-1 * DerStart[0]) + Derfy(Next[1]) * (-1 * DerStart[1])

                if abs(DerfNext) <= epsilon:
                    LocList.append(Next)
                    Start = Next
                    epsilon /= 1.1
                    break

    plotList = list()
    if mode == "momentum":
        c = "tab:red"
    else:
        c = "tab:green"

    for (x, y) in LocList:
        plotList.append((x, y))
        plt.scatter(x, y, s=30, facecolor="none", edgecolors=c, marker='o')
        if len(plotList) < 2:
            continue
        else:
            plt.plot([plotList[0][0], plotList[1][0]], [plotList[0][1], plotList[1][1]], c=c)
            plotList.pop(0)

if __name__ == '__main__':
    DrawBackGround()
    GradientDescent(mode="SGD")
    GradientDescent(mode="momentum")
    plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83

$\text{Reference}$：
谈谈优化算法之一（动量法、Nesterov法、自然梯度法）
深度学习（一）优化算法之动量法详解