今天我们来探讨逆元在ACM-ICPC竞赛中的应用,逆元是一个很重要的概念,必须学会使用它。
对于正整数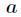 和
和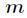 ,如果有
,如果有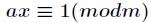 ,那么把这个同余方程中
,那么把这个同余方程中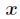 的最小正整数解叫做
的最小正整数解叫做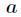 模
模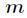 的逆元。
的逆元。
逆元一般用扩展欧几里得算法来求得,如果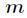 为素数,那么还可以根据费马小定理得到逆元为
为素数,那么还可以根据费马小定理得到逆元为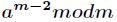 。
。
推导过程如下
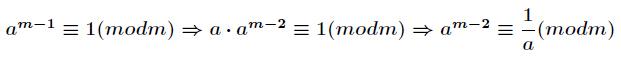
求现在来看一个逆元最常见问题,求如下表达式的值(已知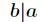 )
)
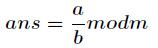
当然这个经典的问题有很多方法,最常见的就是扩展欧几里得,如果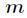 是素数,还可以用费马小定理。
是素数,还可以用费马小定理。
但是你会发现费马小定理和扩展欧几里得算法求逆元是有局限性的,它们都会要求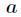 与
与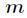 互素。实际上我们还有一
互素。实际上我们还有一
种通用的求逆元方法,适合所有情况。公式如下
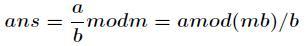
现在我们来证明它,已知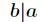 ,证明步骤如下
,证明步骤如下
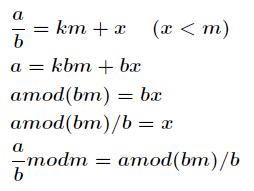
接下来来实战一下,看几个关于逆元的题目。
题目:http://poj.org/problem?id=1845
题意:给定两个正整数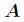 和
和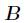 ,求
,求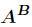 的所有因子和对9901取余后的值。
的所有因子和对9901取余后的值。
分析:很容易知道,先把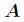 分解得到
分解得到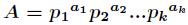 ,那么得到
,那么得到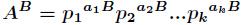 ,那么
,那么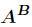
的所有因子和的表达式如下
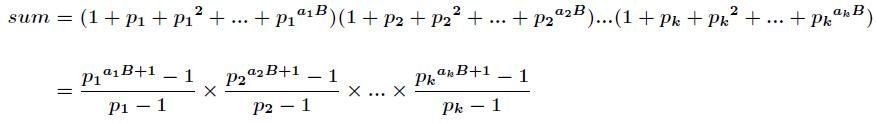
所以我们有两种做法。第一种做法是二分求等比数列之和。
代码:
- #include
- #include
- #include
-
- using namespace std;
- typedef long long LL;
- const int N = 10005;
- const int MOD = 9901;
-
- bool prime[N];
- int p[N];
- int cnt;
-
- void isprime()
- {
- cnt = 0;
- memset(prime,true,sizeof(prime));
- for(int i=2; i
- {
- if(prime[i])
- {
- p[cnt++] = i;
- for(int j=i+i; j
- prime[j] = false;
- }
- }
- }
-
- LL power(LL a,LL b)
- {
- LL ans = 1;
- a %= MOD;
- while(b)
- {
- if(b & 1)
- {
- ans = ans * a % MOD;
- b--;
- }
- b >>= 1;
- a = a * a % MOD;
- }
- return ans;
- }
-
- LL sum(LL a,LL n)
- {
- if(n == 0) return 1;
- LL t = sum(a,(n-1)/2);
- if(n & 1)
- {
- LL cur = power(a,(n+1)/2);
- t = (t + t % MOD * cur % MOD) % MOD;
- }
- else
- {
- LL cur = power(a,(n+1)/2);
- t = (t + t % MOD * cur % MOD) % MOD;
- t = (t + power(a,n)) % MOD;
- }
- return t;
- }
-
- void Solve(LL A,LL B)
- {
- LL ans = 1;
- for(int i=0; p[i]*p[i] <= A; i++)
- {
- if(A % p[i] == 0)
- {
- int num = 0;
- while(A % p[i] == 0)
- {
- num++;
- A /= p[i];
- }
- ans *= sum(p[i],num*B) % MOD;
- ans %= MOD;
- }
- }
- if(A > 1)
- {
- ans *= sum(A,B) % MOD;
- ans %= MOD;
- }
- cout<
- }
-
- int main()
- {
- LL A,B;
- isprime();
- while(cin>>A>>B)
- Solve(A,B);
- return 0;
- }
第二种方法就是用等比数列求和公式,但是要用逆元。用如下公式即可
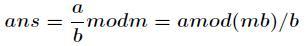
因为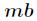 可能会很大,超过int范围,所以在快速幂时要二分乘法。
可能会很大,超过int范围,所以在快速幂时要二分乘法。
代码:
- #include
- #include
- #include
-
- using namespace std;
- typedef long long LL;
- const int N = 10005;
- const int MOD = 9901;
-
- bool prime[N];
- int p[N];
- int cnt;
-
- void isprime()
- {
- cnt = 0;
- memset(prime,true,sizeof(prime));
- for(int i=2; i
- {
- if(prime[i])
- {
- p[cnt++] = i;
- for(int j=i+i; j
- prime[j] = false;
- }
- }
- }
-
- LL multi(LL a,LL b,LL m)
- {
- LL ans = 0;
- a %= m;
- while(b)
- {
- if(b & 1)
- {
- ans = (ans + a) % m;
- b--;
- }
- b >>= 1;
- a = (a + a) % m;
- }
- return ans;
- }
-
- LL quick_mod(LL a,LL b,LL m)
- {
- LL ans = 1;
- a %= m;
- while(b)
- {
- if(b & 1)
- {
- ans = multi(ans,a,m);
- b--;
- }
- b >>= 1;
- a = multi(a,a,m);
- }
- return ans;
- }
-
- void Solve(LL A,LL B)
- {
- LL ans = 1;
- for(int i=0; p[i]*p[i] <= A; i++)
- {
- if(A % p[i] == 0)
- {
- int num = 0;
- while(A % p[i] == 0)
- {
- num++;
- A /= p[i];
- }
- LL M = (p[i] - 1) * MOD;
- ans *= (quick_mod(p[i],num*B+1,M) + M - 1) / (p[i] - 1);
- ans %= MOD;
- }
- }
- if(A > 1)
- {
- LL M = MOD * (A - 1);
- ans *= (quick_mod(A,B+1,M) + M - 1) / (A - 1);
- ans %= MOD;
- }
- cout<
- }
-
- int main()
- {
- LL A,B;
- isprime();
- while(cin>>A>>B)
- Solve(A,B);
- return 0;
- }
其实有些题需要用到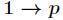 模
模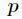 的所有逆元,这里
的所有逆元,这里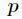 为奇质数。那么如果用快速幂求时间复杂度为
为奇质数。那么如果用快速幂求时间复杂度为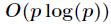 ,
,
如果对于一个1000000级别的素数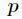 ,这样做的时间复杂度是很高了。实际上有
,这样做的时间复杂度是很高了。实际上有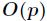 的算法,有一个递推式如下
的算法,有一个递推式如下
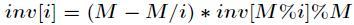
它的推导过程如下,设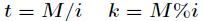 ,那么
,那么
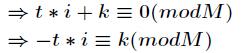
对上式两边同时除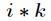 ,进一步得到
,进一步得到
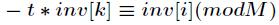
再把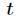 和
和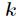 替换掉,最终得到
替换掉,最终得到
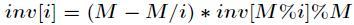
初始化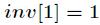 ,这样就可以通过递推法求出
,这样就可以通过递推法求出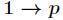 模奇素数
模奇素数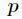 的所有逆元了。
的所有逆元了。
另外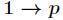 模
模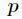 的所有逆元值对应
的所有逆元值对应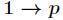 中所有的数,比如
中所有的数,比如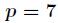 ,那么
,那么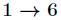 对应的逆元是
对应的逆元是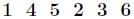 。
。
题目:http://www.lydsy.com/JudgeOnline/problem.php?id=2186
题意:求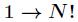 中
中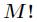 互质的数的个数,其中
互质的数的个数,其中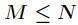 。
。
分析:因为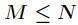 ,所以
,所以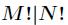 ,我们很容易知道如下结论
,我们很容易知道如下结论
对于两个正整数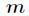 和
和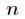 ,如果
,如果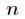 是
是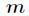 的倍数,那么
的倍数,那么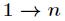 中与
中与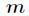 互素的数的个数为
互素的数的个数为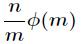
本结论是很好证明的,因为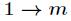 中与
中与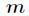 互素的个数为
互素的个数为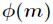 ,又知道
,又知道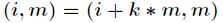 ,所以
,所以
结论成立。那么对于本题,答案就是
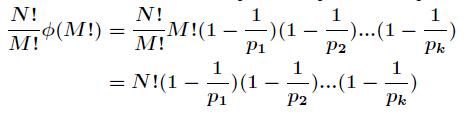
其中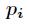 为小于等于
为小于等于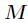 的所有素数,先筛选出来即可。由于最终答案对一个质数取模,所以要用逆元,这里
的所有素数,先筛选出来即可。由于最终答案对一个质数取模,所以要用逆元,这里
求逆元就有技巧了,用刚刚介绍的递推法预处理,否则会TLE的。
代码:
- #include
- #include
- #include
- #include
-
- using namespace std;
- typedef long long LL;
- const int N = 10000005;
-
- bitset
prime; -
- void isprime()
- {
- prime.set();
- for(int i=2; i
- {
- if(prime[i])
- {
- for(int j=i+i; j
- prime[j] = false;
- }
- }
- }
-
- LL ans1[N],ans2[N];
- LL inv[N];
-
- int main()
- {
- isprime();
- int MOD,m,n,T;
- scanf("%d%d",&T,&MOD);
- ans1[0] = 1;
- for(int i=1; i
- ans1[i] = ans1[i-1] * i % MOD;
- inv[1] = 1;
- for(int i=2;i
- {
- if(i >= MOD) break;
- inv[i] = (MOD - MOD / i) * inv[MOD % i] % MOD;
- }
- ans2[1] = 1;
- for(int i=2; i
- {
- if(prime[i])
- {
- ans2[i] = ans2[i-1] * (i - 1) % MOD;
- ans2[i] = ans2[i] * inv[i % MOD] % MOD;
- }
- else
- {
- ans2[i] = ans2[i-1];
- }
- }
- while(T--)
- {
- scanf("%d%d",&n,&m);
- LL ans = ans1[n] * ans2[m] % MOD;
- printf("%lld\n",ans);
- }
- return 0;
- }
接下来还有一个关于逆元的有意思的题目,描述如下

证明:由
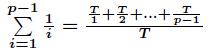
其中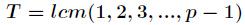
所以只需要证明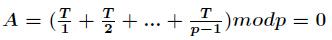 ,而我们知道
,而我们知道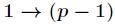 模
模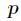 的逆元对应全部
的逆元对应全部
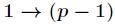 中的所有数,既是单射也是满射。
中的所有数,既是单射也是满射。
所以进一步得到
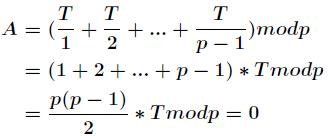
证明完毕!
弹性分组环(Resilient Packet Ring,RPR)是一种采用环型拓扑的城域网技术。2004年公布的IEEE 802.17标准定义了RPR的介质访问控制方法、物理层接口以及层管理参数,并提出了用于环路检测和配置、失效恢复以及带宽管理的一系列协议。802.17标准也定义了环网与各种物理层的接口和系统管理信息库。RPR系统是由两个独立的、方向相反的单向环组合成的双环结构。一个单向环由一系列相连的节点组成,每个节点具有相同的数据速率,但可能具有不同的延时特性。RPR环上的节点数最多为255个,最长距离为2000km,数据传输速率可达10Gbit/s。
![]()
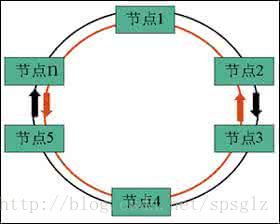
弹性分组环(RPR)技术来源于Cisco公司2000年提出的DPT城域网解决方案.DPT可以使Cisco公司的吉比特交换路由器(GSR)在组网时共享同一带宽,并具有完善的保护倒换能力,可以达到电信级运营的要求。随后,Nortel公司基于自己设备的特点提出了IPT解决方案与Cisco公司抗衡。新兴的Luninous公司也推出了具有自己特色的解决方案RPT。这些方案虽然基本思路相似,但具体的实现方法却有很大的不同,包括在环上传输的包的封装结构、带宽共享控制协议、保护倒换协议和QoS策略等。RPR技术集IP的智能化、以太网的经济性以及光纤环网的高带宽效率和可靠性于一体,为宽带IP城域网运营商提供了一个良好的组网方案。RPR技术使得运营商在城域网内以低成本提供电信级的服务成为可能,在提供类似SDH级网络可靠性的同时还降低了传送费用。RPR有别于传统的MAC,它最吸引人的特点是具有电信级的可靠性,使其不仅仅只是局限于处理面向数据的业务传送需求,同时可以形成处理多业务传送的综合传输解决方案。可以这样说,RPR是IP技术与光网络技术直接融合的产物,它源于客户对IP业务发展的需求,顺应最新的技术潮流,为IP城域网的建设带来了一套低成本、高品质的解决方案。
工作原理
正常情况下两个环同时工作,当一个环发生故障时则由另一个环承担所有帧的传输。环网上的节点共享带宽,不需要进行电路指配。利用公平控制算法环网上的各个节点能够自动地完成带宽协调,弹性分组环(RPR)中每一个节点都执行SRP公平算法。每个节点都有一个环形网络拓扑图,都能将数据发送到光纤子环上,迭往目的节点。两个子环都可作为工作通道。为了防止光纤或节点故障发生时导致链路中断,利用保护算法来消除相应的故障段。
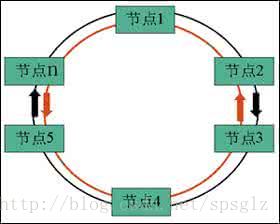
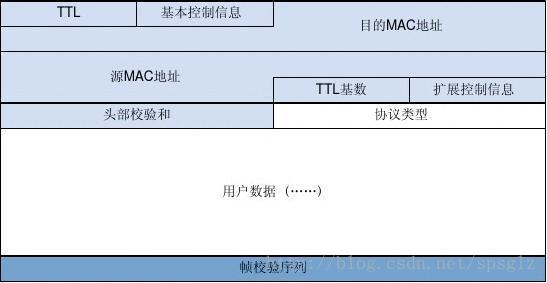
环中传送的帧类型可以包括单播帧、多播帧和组播帧。单播帧与多播帧及组播帧的处理方式是不相同的。单播帧由目的节点将数据帧接收并将其从环网上删除。多播帧及组播帧采用广播方式在环网中传输一周后,由源节点将其从环网上删除,同时为了防止帧在网上的无限循环,帧结构中还设置了TTL字段,帧每经过一个节点,TTL值减I,当TTL值为0时,收到该帧的任意点都将其从网上删除。
体系结构
MAC服务接口提供上层协议的服务原语:MAC控制子层控制MAC数据通路,维护MAC状态,并协调各种MAC功能的相互作用:MAC数据通路子层提供数据传输功能:MAC子层通过PHY服务接口发送/接收分组。
RPR采用了双环结构,由内层的环1(ringlet1)和外层的环0(ringlet O)组成,每个环都是单方向传送。相邻工作站之间的跨距(span)包含传送方向相反的两条链路(Link)。如果x站接收Y站发出的分组,则x是Y的下游站,而Y是x的上游站。RPR支持多达255个工作站,最大环周长为2000km。
关键技术
(1)业务类型。RPR支持3种业务。A类业务提供保证的带宽,提供与传输距离无关的很小的延迟抖动,适合语音、视频等电路仿真应用;B类业务提供保证的带宽,提供与传输距离相关的有限的延迟抖动,可以超信息速率(Excess Information Rate,EIR)传输,适合企业数据传输方面的应用;C类业务提供尽力而为的服务,适合用户的因特网接入。
(2)空间复用。RPR的空间复用协议(SpatialReuse Protocol,SRP)提供了寻址、读取分组、管理带宽和传播控制信息等功能。在RPR环上,数据帧被目标站从环上剥离,而不是像其他环网那样返回源节点后被剥离。这样就使得多个节点分成多段线路同时传输数据,充分利用了整个环路的带宽。例如,环上依次有A、B、C、D这4个节点,分组经过A节点到达B节点被剥离,另外的分组可以从B节点插入,并经C传送到D节点,从而有效地利用了环上A到D之间的带宽。
(3)拓扑发现。RPR拓扑发现是一种周期性活动,也可以由某个需要知道拓扑结构的节点发起。在拓扑发现过程中,拓扑发现分组经过的节点把自己的标识符加入到分组中的标识符队列,产生一个新的拓扑发现分组,这样就形成了拓扑识别的累积效应。通过拓扑发现,节点可以选择最佳的插入点,使得源节点到达目的节点的跳步数最小。
(4)公平算法。公平算法是一种保证环上所有站点公平地分配带宽的机制。如果一个节点发生阻塞,它就会在相反的环上向上游节点发送一个公平帧。上游站点收到这个公平帧时就调整自己的发送速率使其不超过公平速率。一般来说,接收到公平帧的站点会根据具体情况作出两种反应:若当前节点阻塞,它就在自己的当前速率和收到的公平速率之间选择一个最小值,并发布给上游节点;若当前节点不阻塞,就不采取任何行动。
(5)环自愈保护。当RPR环中出现严重故障或者发生光纤中断后,中断处的两个站点就会发出控制帧,沿光纤方向通知各个节点。正要发送数据的站点接收到这个消息后,立即把要发送的数据倒换到另一个方向的光纤上。一般来说,在环保护切换时,要按照业务流的不同服务等级、根据相同目标一起倒换原则依次向反向光纤倒换业务。RPR和SDH一样,能保证业务的倒换时问少于50ms。
特点
(1)传输带宽的有效利用。首先,正常情况下两个环都作为工作通道,大大节约了光纤资源。同时还保留了当出现环网故障时作为备份通道的特性。其次,在RPR中利用空间重用技术实现同一环上同时传输多个数据帧或不同环同一跨距上传输不同数据帧。
(2)环间的自动切换保护。RPR技术提供两种环间的自动切换保护方式:环回方式和源节点切换方式。
①环回方式:在这种方式下,当节点检测到传输链路出现故障时,并不立即进行环保护切换,而是将帧继续向原环发送。当帧到达故障点(设备故障或传输介质故障)时,若此时故障点具有环回功能,则由故障点将帧进行环回,通过另一环进行传输。
②源节点切换方式:在这种方式下,当节点检测到传输链路出现故障时,立即将进入本节点的数据帧通过另一环传输出去,而终止向故障环的数据帧发送。
两种方式各具有其自身的优缺点。环回方式在故障点具有环回功能时,结构简单,数据包丢失少,但占用带宽多。源节点切换方式的优缺点正好与环回方式相反。无论那种方式,其切换时间均能达到50ms。
(3)可靠的服务质量保证。RPR环网上的节点针对业务动态分配带宽,工作、业务、统计、复用共享带宽,不需要进行电路型的预指配。支持3种业务类型:A类、B类和C类。
A类:保证信息速率(CIR)业务,需要固定分配带宽。这种业务支持有保证的带宽、低时延、低时延抖动的应用。适合语音、视频、电路仿真业务的应用。对于这类业务RPR采用预留带宽的方式予以保证。
B类:支持有保证信息速率和附加信息速率(EIR)。其中,CIR需要预分配带宽,而EIR并不预指派带宽而是通过公平算法动态获取带宽。B类业务对时延抖动要求低于A类,但仍然有指标要求。适合多种企业级的业务应用。对于这类业务中的有最低保证速率的业务采用带宽预留的方式,而对于附加流量,则自动参与公平算法。
c类:尽力传送业务。不分配带宽,不能保证数据传送速率、也不保证严格的时延抖动指标,适合IP业务的应用。对于这类业务则完全参与动态的带宽分配算法。
(4)自动拓扑发现。这个功能是RPR中各项主要功能的基础。在RPR中可以实现即插即用,RPR通过拓扑发现协议精确识别网中各节点以及节点间链路的状态及配置情况。每个节点都有一个拓扑数据库,共同维护整个环网的拓扑结构。在新节点加入,节点发生故障或删除时,节点将自动发送TP(Topology and Protection TP)帧。环上其他节点接收到这些帧并修改自己的拓扑数据库,一旦拓扑收敛,则当前拓扑立即生效。[3]
注:本文转载自blog.csdn.net的ACdreamers的文章"http://blog.csdn.net/acdreamers/article/details/8220787"。版权归原作者所有,此博客不拥有其著作权,亦不承担相应法律责任。如有侵权,请联系我们删除。


评论记录:
回复评论: