来看看在MRI领域,扩散模型在重建、生成、转译、分割和异常检测上的光芒吧~
原文传递:A Survey of Emerging Applications of Diffusion Probabilistic Models in MRI
综述系列篇:
【SAM综述】医学图像分割的分割一切模型:当前应用和未来方向
【CLIP综述】CLIP在医学影像中的应用(一)
【CLIP综述】CLIP在医学影像中的应用(二)
【Diffusion综述】医学图像分析中的扩散模型(一)
【Diffusion综述】医学图像分析中的扩散模型(二)
0、摘要
扩散概率模型(DPMs)采用显式似然表征和逐步采样过程来合成数据,获得了广泛的研究兴趣。尽管因为采样过程中涉及大量的步骤,其具有较大的计算负担,但由于其高质量和多样性的生成,在各种医学成像任务中得到了广泛的重视。(可阅读 “医学图像分析中的扩散模型” )
磁共振成像(MRI)是一种重要的医学成像方式,具有优异的软组织对比度和较高的空间分辨率,为 DPMs 大展拳脚创造了机会。(我为MRI抗大旗~)
尽管最近探索 MRI 中的 DPMs 的研究激增,但一篇专门为 MRI 应用而设计的 DPMs 的综述论文仍然缺乏。(我要做第一)本文旨在帮助MRI研究人员了解DPMs在不同领域的应用进展。
本文介绍了两种主要的 DPMs 的理论,并根据扩散时间步长是离散的还是连续的进行了分类,然后对 MRI 中的 DPMs 进行了全面的综述,包括重建、图像生成、图像转译、分割、异常检测以及进一步的研究方向。最后,讨论了 DPMs 的一般局限性以及特定于MRI任务的局限性,并指出了值得进一步探索的潜在领域。
1、引言
磁共振成像(MRI)以其优越的软组织对比度、无创性和多平面成像能力,已成为医学诊断和治疗的重要成像方式。然而,它也受到复杂的成像原理、长扫描时间和高经济成本的限制,这可能会阻碍其充分发挥临床应用的潜力。(实际临床中,扫得慢,不好约)
近年来,生成式人工智能(AI)模型的蓬勃发展,为解决与MRI相关的挑战提供了新的和有前途的解决方案。例如,一些工作将变分自动编码器(VAE)应用于MRI的合成和重建。一些研究提出了基于生成对抗网络(GAN)的MR图像异常检测、重建和超分辨率设计模型。这些模型引导高质量的图像生成、数据驱动的优化方法和潜在的具有成本效益的应用程序集成。
然而,VAE 受到后验分布和先验分布形成的限制,需要在结构复杂性和模型表征能力之间进行权衡,并且倾向于生成低保真度的样本。归一化流(Normalization Flow)能够精确计算概率似然函数,但受到模型每次变换可逆要求的约束,限制了模型的设计。自回归模型(Autoregressive Models)作为另一种经典的生成模型,也面临着生成速度慢、解码空间大、难以生成高分辨率图像等问题。近年来,GAN表现出了出色的生成性能,但其对抗性学习机制导致训练不稳定。(主流生成模型各有不足)
图1:扩散模型在医学影像中的发展与在MRI中的应用
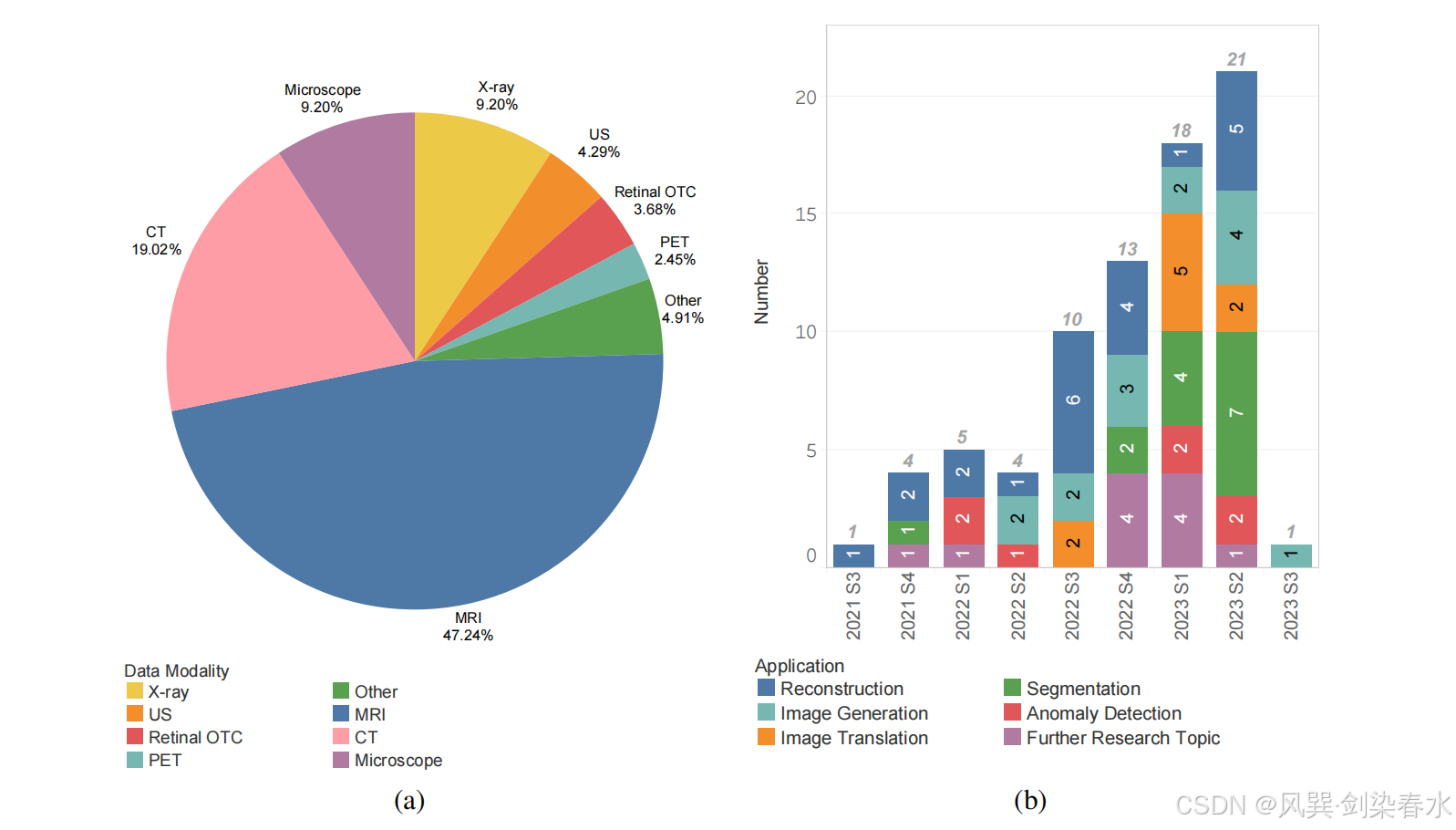
DPMs 作为一种新兴的生成模型,由于其完善的数学解释、无对抗性的训练策略以及能够实现稳定可控的生成,在医学成像领域受到了广泛的关注。
通过收集2021年至2023年第三季度出现的在医学成像中应用DPMs的所有方法,并分析图1(a)中的相关数据模式,本文发现约47.24%的方法集中于MRI。此外,图1(b)总结了近年来DPMs在MRI中的应用研究,表明DPMs在MRI中的应用呈现出范围扩大、数量增加的快速发展趋势。这一趋势归因于DPMs在满足MRI需求方面的独特优势。(我倒要看看有什么特殊)
MRI作为一种多功能的诊断工具,可以产生丰富的对比进行全面的诊断,但也面临着一些长期存在的挑战,如采集速度慢,易受运动的影响。
DPMs除了能够解决MRI重建的逆问题外,得益于其独特的噪声估计设置,重建过程还伴随着图像的去噪,可以同时实现加速重建和降噪。此外,条件DPMs的更好的数学解释为图像合成提供了更稳定和可靠的方法,可用于将一个或多个MRI模态转换为目标模态或在MRI和其他成像方式之间转换。
此外,出色的生成性能使其成为理解功能性MRI的新工具。因此,全面回顾和深入分DPMs在MRI中的新兴应用具有重要意义。
本文希望这篇论文能成为对这个快速发展的重要领域感兴趣的MRI研究人员的一个良好起点,本文的主要贡献体现在以下几个方面:
(1)DPMs基本原理的整体概述: 本文从扩散时间步长形成的角度,总结了目前两类主要的DPMs模型的原理,揭示了两类模型之间的关系,并对条件DPMs进行了阐述;
(2)DPMs在MRI中的应用综述: 详细描述了将DPMs应用于MRI中不同任务的研究,包括图像重建、图像生成和转译、分割和异常检测等著名的课题,以及其他开创性的研究主题,如配准、运动校正、超分辨率和其他新兴的下游应用;
(3)对趋势和挑战的深入讨论: 深入讨论了将DPMs应用于MRI的趋势和挑战,揭示了DPMs的未来发展方向,包括模型设计和扩展应用;
2、理论
扩散概率模型(DPMs),生成模型的新范式,提出使用神经网络估计的一系列高斯噪声
ϵ
t
∼
N
(
µ
t
,
σ
t
)
{ϵ_t∼\mathcal{N}(µ_t, σ_t)}
ϵt∼N(µt,σt) 可以将数据
x
{x}
x 扰动为具有标准正态分布
z
∼
N
(
0
,
I
)
{z∼\mathcal{N}(0, I)}
z∼N(0,I) 的噪声(称为“扩散过程”),然后逐渐从
z
{z}
z 恢复数据样本
x
^
{ \hat x}
x^(称为“反向过程”)。图2展示了扩散过程和反向过程:
图2:扩散概率模型(DPMs)中的扩散过程和反向过程
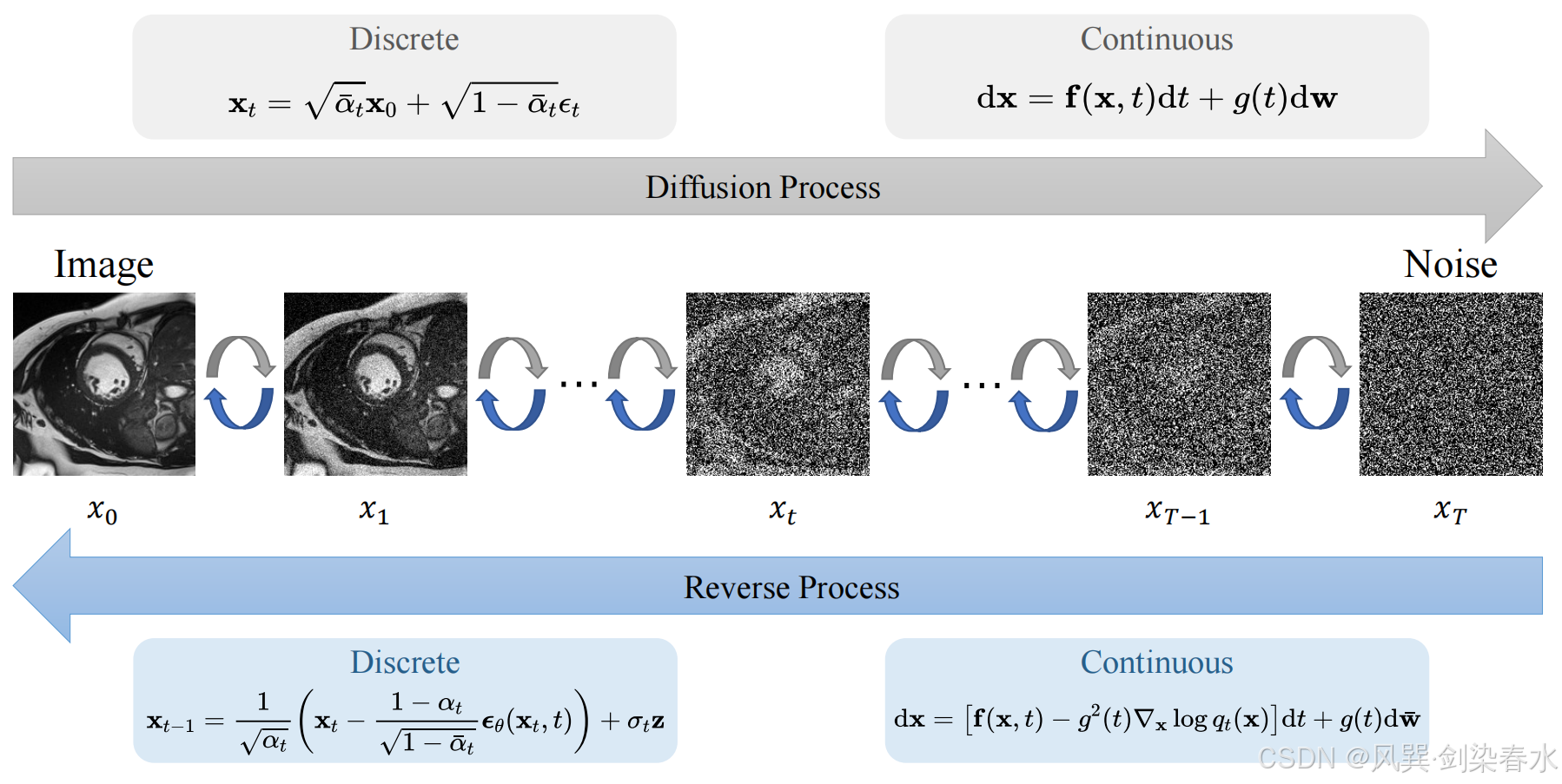
对不同扩散时间步长下的表示估计产生了两种扩散概率模型:涉及噪声估计和马尔可夫链的离散时间扩散模型和涉及分数匹配和随机微分方程(SDEs)的连续时间扩散模型。
2.1、离散时间扩散模型(Discrete-time Diffusion Models)
2.1.1、DDPM
Sohl-Dickstein等人首先介绍了DPMs的原理,它利用生成式马尔可夫链将一个简单的已知分布转化为目标分布。
对于一个给定的数据分布
q
(
x
0
)
{q(x_0)}
q(x0),扩散过程由转移概率为
q
(
x
t
∣
x
t
−
1
)
{q(x_t |x_{t-1})}
q(xt∣xt−1) 的离散时间马尔科夫链
{
x
t
,
0
≤
t
≤
T
,
t
∈
N
}
{\{x_t, 0≤t≤T, t \in \mathbb{N} \}}
{xt,0≤t≤T,t∈N} 表征,根据马尔可夫性质,等式(1)给出了
q
(
x
0
)
{q(x_0)}
q(x0) 与马尔可夫链的平稳分布
p
(
x
T
)
∼
N
(
0
,
I
)
{p(x_T)∼\mathcal{N}(0, I)}
p(xT)∼N(0,I) 的关系:
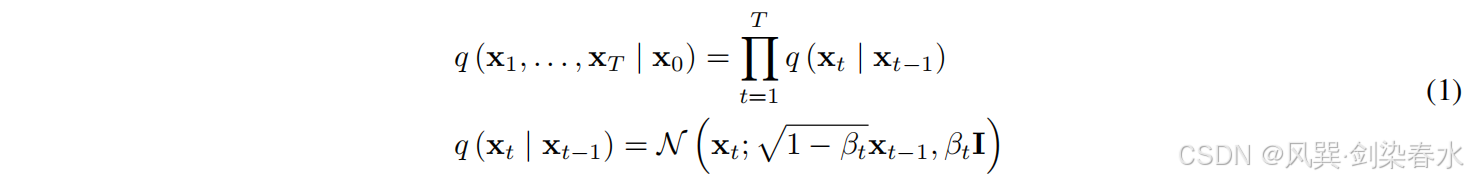
其中,噪声调度
β
t
∈
(
0
,
1
)
{β_t∈(0,1)}
βt∈(0,1) 是一组通常设置为线性增加的超参数,反映了每次转移时原始信号中加入的噪声水平。
令
α
t
=
1
−
β
t
{α_t=1−β_t}
αt=1−βt,
α
ˉ
t
=
∏
i
=
0
t
α
i
{{\bar \alpha _t} = \prod _{i = 0}^t{\alpha _i}}
αˉt=∏i=0tαi,利用等式(2)将一个样本数据
x
0
∼
p
(
x
0
)
{x_0∼p(x_0)}
x0∼p(x0) 转换为噪声数据
x
T
{x_T}
xT:(前向过程)
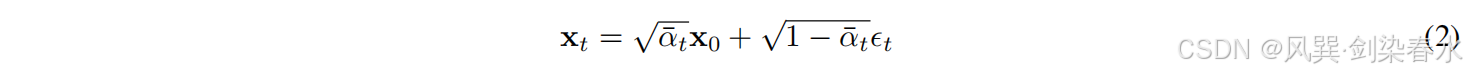
对于反向过程,反向时间马尔可夫链的转移是近似为可学习的条件概率 p θ ( x t − 1 ∣ x t ) {p_θ(x_{t-1} | x_t)} pθ(xt−1∣xt),如等式(3)所示:
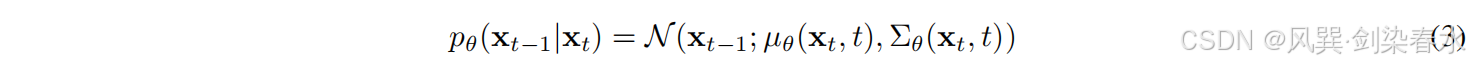
其中,均值
μ
θ
(
x
t
,
t
)
{{\mu _\theta }\left( {{x_t},t} \right)}
μθ(xt,t) 和方差
∑
θ
(
x
t
,
t
)
=
σ
t
2
I
{\sum\nolimits_\theta {\left( {{x_t},t} \right)} =σ_{t}^{2}I}
∑θ(xt,t)=σt2I 由神经网络
ϵ
θ
(
x
t
,
t
)
{ϵ_θ(x_t, t)}
ϵθ(xt,t) 学习,其参数为
θ
{θ}
θ。其中,
σ
t
{σ_t}
σt 通常被固定为
β
t
{β_t}
βt 或
β
~
t
=
1
−
α
ˉ
t
−
1
1
−
α
ˉ
t
β
t
{{\tilde \beta _t} = \frac{{1 - {{\bar \alpha }_{t - 1}}}}{{1 - {{\bar \alpha }_t}}}{\beta _t}}
β~t=1−αˉt1−αˉt−1βt,因此,我们可以首先从
x
T
∼
p
(
x
T
)
{x_T∼p(x_T)}
xT∼p(xT) 采样,然后根据学习到的
p
θ
(
x
t
−
1
∣
x
t
)
{p_θ(x_{t−1}|x_t)}
pθ(xt−1∣xt) 迭代采样
x
t
−
1
{x_{t−1}}
xt−1,直到
t
=
1
{t = 1}
t=1,得到生成的结果
x
^
0
∼
p
(
x
0
)
{\hat x_0∼p(x_0)}
x^0∼p(x0),这种采样过程可以被描述为等式(4):
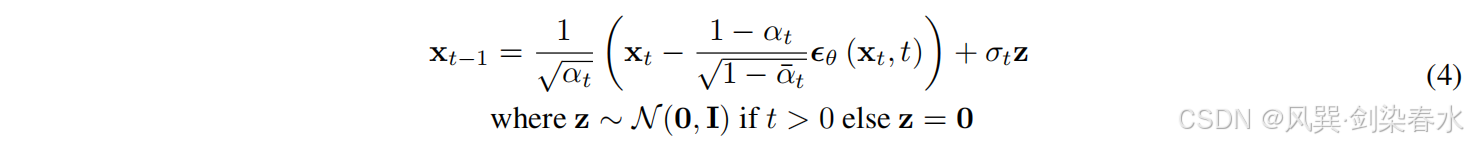
对于网络优化,Sohl-Dickstein等人和Ho等人指出,可以通过最小化负对数似然的变分界推导出简化的优化目标:
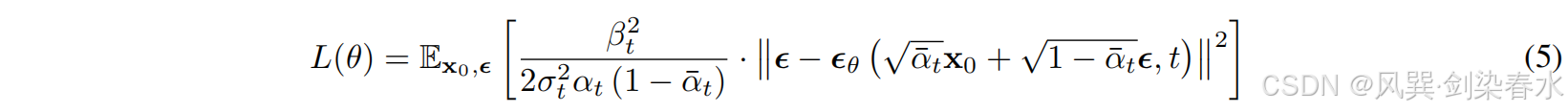
Ho等通过比较,指出等式(5)可以简化为等式(6),其中 t {t} t 在 1 {1} 1 和 T {T} T 之间是均匀分布的,从等式(5)到等式(6),我们可以看到等式(5)忽略了等式(6)中两个噪声的权重。除了简化优化目标之外,这种简化还可以减少对少量噪声扰动的估计权重,从而使网络能够在图像中添加大量噪声时专注于更困难的估计。等式(6)的实验结果较好,在实践中使用频率较高。
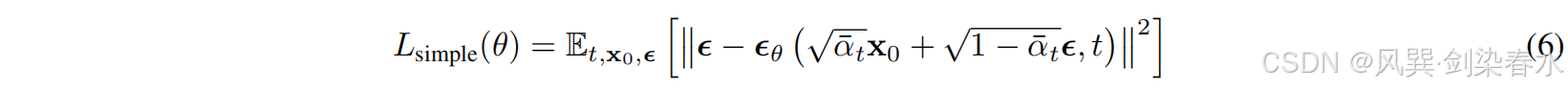
事实上, ϵ θ {ϵ_θ} ϵθ 估计了由等式(2)描述的扩散过程中添加到 x t {x_t} xt 的噪声。因此,等式(4)是去噪模型,反向过程表示去除高斯噪声,得到干净的图像。
2.1.2、DDIM
DDPM的一个主要限制是它的生成时间长,这是因为需要沿着马尔可夫链迭代地模拟去噪的结果。与使用马尔可夫性质的DDPM不同,去噪扩散隐式模型(DDIM)通过直接定义不依赖于扩散过程的
q
(
x
t
−
1
∣
x
t
,
x
0
)
{q(x_{t−1}|x_t, x_0)}
q(xt−1∣xt,x0) 来实现采样加速,因此可以通过在逆向过程中穿越部分中间状态来减少迭代次数。
更重要的是,当
x
T
{x_T}
xT 固定时,由于生成是确定的,因此以一个潜在变量为条件的多个样本应该具有相似的高级特征,这构成了条件扩散概率模型的基础。
DDIM的扩散过程和训练目标与DDPM相似,对于反向过程,DDIM提出将
q
(
x
t
−
1
∣
x
t
,
x
0
)
{q(x_{t−1}|x_t, x_0)}
q(xt−1∣xt,x0) 替换为
q
σ
(
x
1
,
.
.
.
,
x
T
∣
x
0
)
=
q
σ
(
x
T
∣
x
0
)
∏
t
=
2
T
q
σ
(
x
t
−
1
∣
x
t
,
x
0
)
{q_σ(x_1,...,x_T|x_0)=q_σ(x_T|x_0)}\prod\limits_{t = 2}^Tq_σ(x_{t-1}|x_t,x_0)
qσ(x1,...,xT∣x0)=qσ(xT∣x0)t=2∏Tqσ(xt−1∣xt,x0),其中
σ
∈
R
≥
0
T
{σ\in \mathbb{R}_{≥0}^T}
σ∈R≥0T是与反向过程相关的生成分布的索引,同时满足:
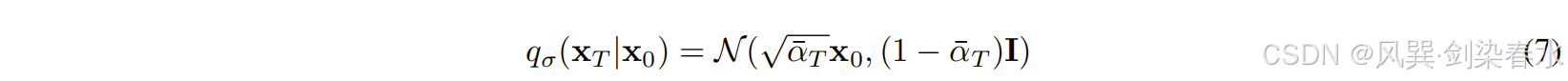
当
1
<
t
<
T
{1
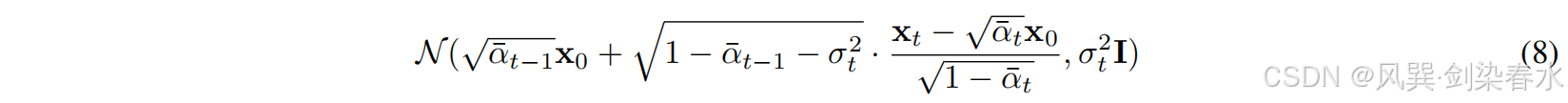
由于相应的“正向过程”意味着每个
x
t
{x_t}
xt 都依赖于
x
t
−
1
{x_{t-1}}
xt−1 和
x
0
{x_0}
x0,所以这个过程是非马尔可夫式的。具体来说,对于反向过程,
p
θ
(
x
t
−
1
∣
x
t
)
{p_θ(x_{t−1}|x_t)}
pθ(xt−1∣xt) 的近似可以从一个标准的正态分布
p
θ
(
x
T
)
=
N
(
0
,
I
)
{p_θ(x_T)= \mathcal{N}(0,I)}
pθ(xT)=N(0,I) 开始,在中间状态
1
<
t
<
T
{1
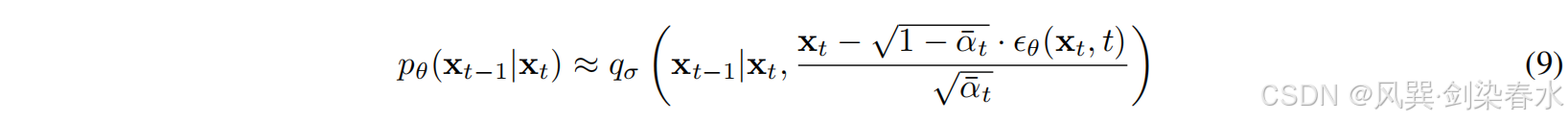
根据上面解释的
p
θ
(
x
t
−
1
∣
x
t
)
{p_θ(x_{t−1}|x_t)}
pθ(xt−1∣xt) 的近似值,从
x
t
{x_t}
xt 到
x
t
−
1
{x_{t-1}}
xt−1 的采样过程可以描述为等式(10)通过使用重新参数化技巧来修改被替换的
q
σ
(
x
t
−
1
∣
x
t
,
x
0
)
{q_σ(x_{t-1}|x_t,x_0)}
qσ(xt−1∣xt,x0)。
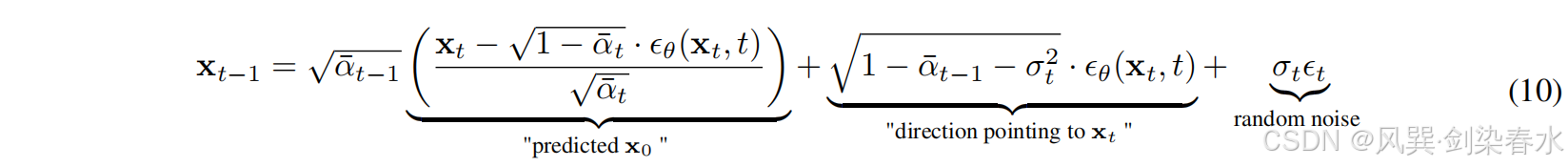
ϵ
t
∼
N
(
0
,
I
)
{ϵ_t ∼ \mathcal{N}(0,I)}
ϵt∼N(0,I) 是独立于
x
t
{x_t}
xt 的标准高斯分布,
ϵ
θ
(
x
t
,
t
)
{ϵ_θ(x_t, t) }
ϵθ(xt,t) 是网络的噪声估计。
直观上,求和右边的第一项直接来自
x
0
{x_0}
x0 给定
x
t
{x_t}
xt 的表示,因此表示预测的
x
0
{x_0}
x0,而求和的第二项来自与等式(8)中
x
t
{x_t}
xt 的边缘相匹配的均值函数的修正,因此表示指向
x
t
{x_t}
xt 的方向。
Song等指出,不同的 σ {σ} σ 选择会导致不同的采样过程。具体来说,让 σ t 2 = η ⋅ β ~ t {σ_t^2 = η·\tilde β_t} σt2=η⋅β~t 和 η ≥ 0 {η≥0} η≥0 是一个与噪声强度相关的超参数,当 η = 1 {η=1} η=1 ,采样过程相当于DDPM,当 η = 0 {η=0} η=0 ,生成时没有随机噪声,并且在生成原始 x T {x_T} xT 时变得确定,此外,可以通过将序列 [ 1 , … , T ] {[1,…,T]} [1,…,T] 替换为其子序列 [ τ 1 , … , τ S ] {[ τ_1,…, τ_S]} [τ1,…,τS], S ≤ T {S≤T} S≤T 来实现等式(10)加速采样。
2.2、连续时间扩散模型(Continuous-time Diffusion Models)
图2中使用这两个过程的扩散概率模型的目标是找到数据分布 q ( x ) {q (x)} q(x) 的一个稳定的迭代模型。当 { x t } {\{x_t\}} {xt} 中的 t {t} t 从离散时间 0 ≤ t ≤ T {0≤t≤T} 0≤t≤T, t ∈ N {t∈\mathbb{N}} t∈N 变为连续场景 t ∈ [ 0 , T ] {t∈[0,T]} t∈[0,T] 时, { x t } {\{x_t\}} {xt} 不再是一个离散时间马尔可夫链,而是一个具有马尔可夫性质的随机过程(即马尔可夫过程),这为扩散概率模型提供了一种新的数学工具。
2.2.1、朗之万动力学的得分匹配
与使用马尔可夫链的DDPM不同,朗之万动力学的得分匹配(SMLD)通过使用神经网络 s θ ( x ) , s θ : R D → R D {s_θ(x),s_θ:\mathbb{R}^D→\mathbb{R}^D} sθ(x),sθ:RD→RD 估计每个噪声尺度上对数似然的梯度梯度 ∇ x log q ( x ) {{\nabla _{x}}\log q(x)} ∇xlogq(x) 来近似概率密度 q ( x ) {q(x)} q(x)。因此,SMLD可以通过替换其归一化常数使基于能量的模型的概率密度可计算。
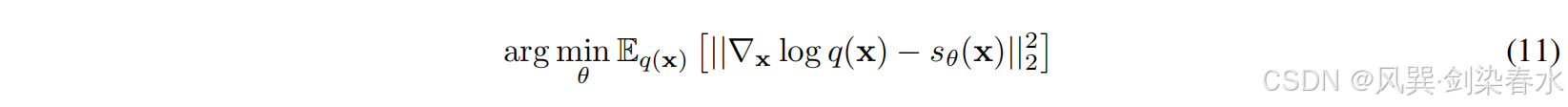
使用
s
θ
(
x
)
{s_θ(x)}
sθ(x) 近似分数
∇
x
log
q
(
x
)
{{\nabla _{x}}\log q(x)}
∇xlogq(x) 的目标可以描述为最小化 Fisher 散度,如等式(11),关于分数匹配的研究提供了在
∇
x
log
q
(
x
)
{{\nabla _{x}}\log q(x)}
∇xlogq(x) 未知时最小化训练集上的 Fisher 散度的方法。
然而,在流形假设下,由于分数匹配的数据点较少,低密度区域的分数函数估计会不准确。特别是,当 q ( x ) {q(x)} q(x) 相对较小时,在等式(12)的积分中忽略了 q ( x ) {q(x)} q(x) 的低密度部分。
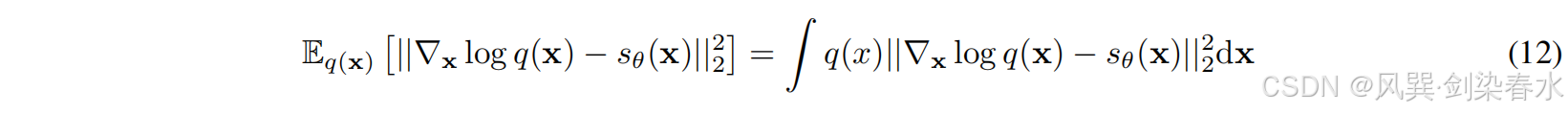
因此,作者在[17]中提出在数据分布中加入不同强度的高斯噪声
ϵ
t
{ϵ_t}
ϵt,如等式(13)。因此,分数函数
∇
x
log
q
(
x
)
{{\nabla _{x}}\log q(x)}
∇xlogq(x) 可以被每个估计的
∇
x
t
log
q
(
x
t
)
{{\nabla _{x_t}}\log q(x_t)}
∇xtlogq(xt) 均匀地覆盖,使得分数估计器
s
θ
(
x
t
)
{s_θ(x_t)}
sθ(xt) 的训练更加稳定。
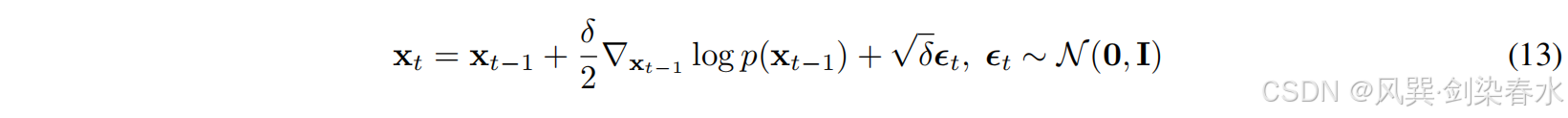
其中 δ {δ} δ 为步长,当 t → T {t→T} t→T 和 T → ∞ {T→∞} T→∞ 时,在小步长 δ → 0 {δ→0} δ→0 下,使用 p ( x t ) {p(x_t)} p(xt) 估计 q ( x ) {q(x)} q(x) 的误差可以足够小。随后,可以使用等式(13)中的随机梯度Langevin Dynamic,利用 s θ ( x t − 1 ) ≈ ∇ x t − 1 log q ( x t − 1 ) {s_θ(x_{t−1})≈{\nabla _{x_{t-1}}}\log q(x_{t-1})} sθ(xt−1)≈∇xt−1logq(xt−1) 得到 q ( x ) {q(x)} q(x)。
2.2.2、基于分数的SDE
基于分数的SDE创新性地从SDE的角度考察了 DPMs。提出扩散过程和反向过程都有对应的SDE,在反向过程中生成样本相当于利用 s θ {s_θ} sθ 得到反向SDE的数值解。本研究还证明了对于所有的扩散过程,都存在一个由常微分方程(ODE)描述的确定性过程,尽管 DDPM 和 SMLD 在理论上很相似,但它也为 DPMs 的理论研究提供了一个统一的视角。
具体来说,由于马尔可夫过程 { x t , t ∈ [ 0 , T ] } {\{x_t, t∈[0,T]\}} {xt,t∈[0,T]} 具有连续的采样路径,基于score的 SDE 提出将扩散过程建模为 Itô SDE 的解,如等式(14)所示:
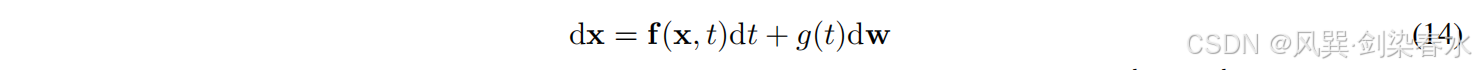
其中
w
{w}
w 是时间
t
{t}
t 从
0
{0}
0 到
T
{T}
T 的标准 Wiener 过程,
f
(
⋅
,
t
)
:
R
d
→
R
d
{f(·,t): \mathbb{R}^d→\mathbb{R}^d}
f(⋅,t):Rd→Rd 是一个向量函数,称为
x
t
{x_t}
xt 的漂移系数,
g
(
⋅
)
:
R
→
R
{g(·): \mathbb{R}→\mathbb{R}}
g(⋅):R→R 是一个标量函数,称为
x
t
{x_t}
xt 的扩散系数,反向过程是方程15的解:
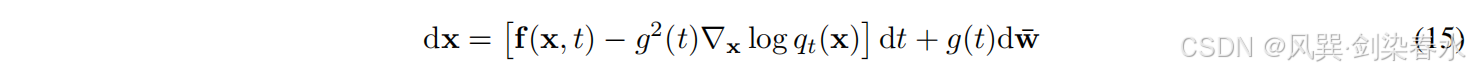
其中,当时间
t
{t}
t 从
T
{T}
T 倒流到
0
{0}
0 时,
w
ˉ
{\bar w}
wˉ 是一个标准的维纳过程,而
d
t
{dt}
dt 是一个无穷小的负时间步长,用
q
t
(
x
)
{q_t(x)}
qt(x) 表示
x
t
{x_t}
xt 的概率密度,训练目标为:
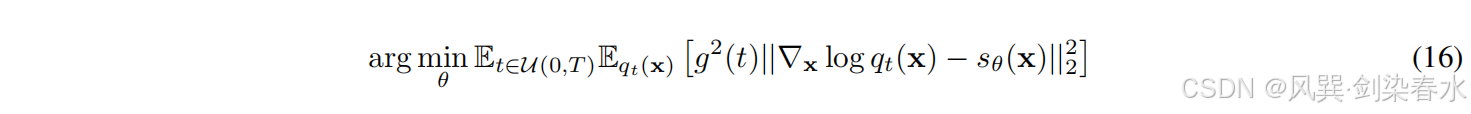
虽然 DDPM 和 SMLD 代表了两种不同的添加噪声的方式,但两者都可以用 SDEs 来表示。对于 DDPM,对应的 SDE 为等式(17),命名为方差保持 SDE(Variance Preserving SDE, VP-SDE),因为它在
t
→
∞
{t→∞}
t→∞ 时给出了一个方差有限的过程。对于 SMLD,对应的 SDE 为等式(18),命名为方差爆炸 SDE(Variance Exploding SDE, VE-SDE),因为它在
t
→
∞
{t→∞}
t→∞ 时产生一个方差爆炸的过程。
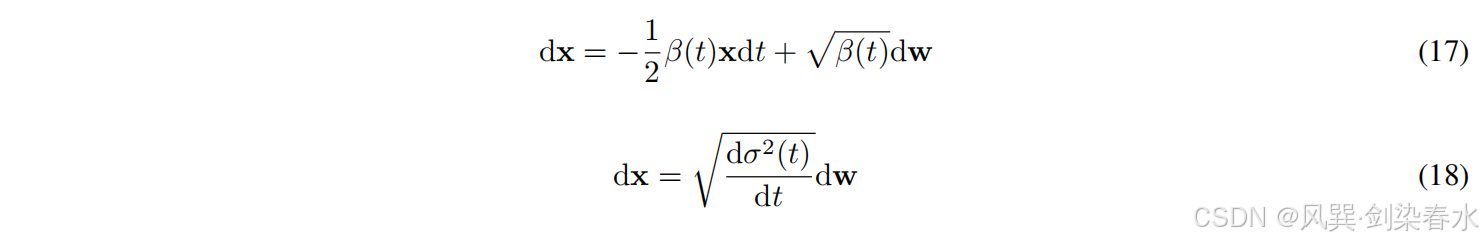
SDE 和 ODE 之间的关系也代表了概率抽样和确定性抽样之间的关系。对于等式(14)中的 SDE,可以表示为等价于下面的等式(19)。由于
σ
(
t
)
d
w
{σ(t)dw}
σ(t)dw 在
σ
(
t
)
≠
0
{σ(t) ≠ 0}
σ(t)=0 时可以带来随机性,因此这种情况为概率抽样。如果方差
σ
(
t
)
=
0
{σ(t) = 0}
σ(t)=0,采样不包含随机性,因此是一个确定性过程,那么我们可以得到如式(20)所示的 ODE。这种确定性抽样也可以看作是一种归一化流,用于估计概率密度和似然。
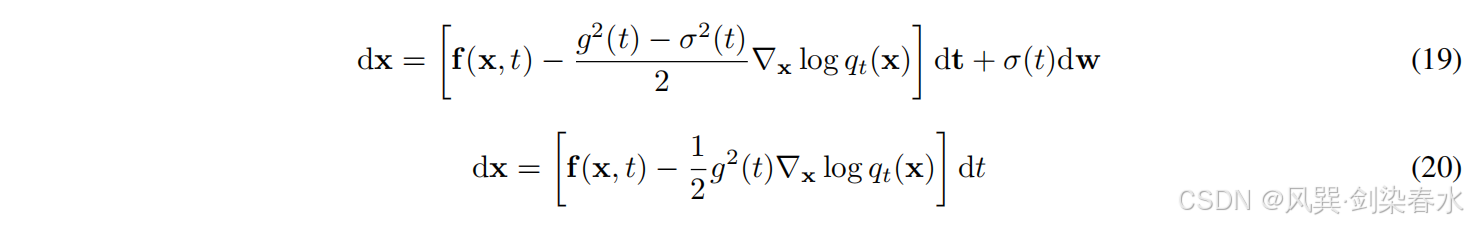
2.3、关系
基于分数的 SDE 的出现为 DPMs 的理论研究提供了一个数学工具,它揭示了离散和连续时间扩散概率模型之间的有用关系。
(1)噪声估计和分数匹配
基于分数的 SDE 揭示了 DDPM 中的噪声估计
ϵ
θ
(
x
t
,
t
)
≈
ϵ
t
{ϵ_θ(x_t, t) ≈ ϵ_t}
ϵθ(xt,t)≈ϵt 与 SMLD 中的分数匹配
s
θ
(
x
t
)
≈
∇
x
t
log
q
(
x
t
)
{s_θ(x_t)≈{\nabla _{x_t}}\log q(x_t)}
sθ(xt)≈∇xtlogq(xt) 之间的特殊关系。特别是,等式(2)表示
q
(
x
t
∣
x
0
)
∼
N
(
α
ˉ
t
x
0
,
(
1
−
α
ˉ
t
)
I
)
{q(x_t|x_0) ∼ \mathcal{N}(\sqrt {{{\bar \alpha }_t}}x_0,(1-{\bar \alpha }_t)I)}
q(xt∣x0)∼N(αˉtx0,(1−αˉt)I),所以可以计算出对数似然的梯度
∇
x
t
log
q
(
x
t
∣
x
0
)
{{\nabla _{x_t}}\log q(x_t|x_0)}
∇xtlogq(xt∣x0):
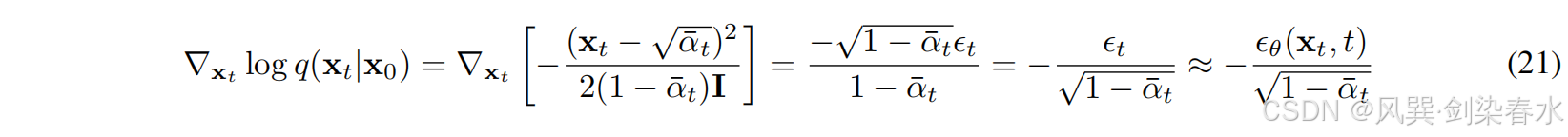
因此,考虑公式(22)中 ∇ x t log q ( x t ∣ x 0 ) {{\nabla _{x_t}}\log q(x_t|x_0)} ∇xtlogq(xt∣x0) 对 q ( x 0 ) {q(x_0)} q(x0) 的期望。等式(11)中的分数匹配等于等式(6)中的噪声估计除以一个常数:
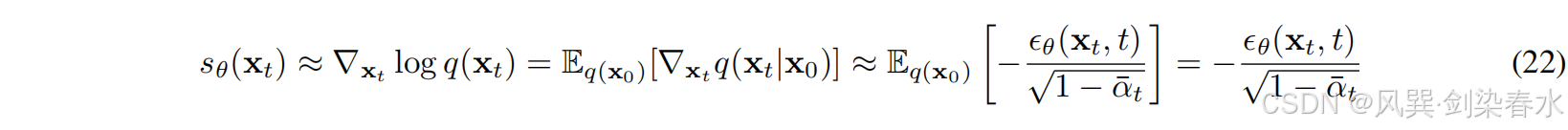
(2)反向采样和SDE(ODE)求解器
离散时间 DPMs 可以从形式上看作是连续时间 SDEs 的离散近似,不同 DPMs 的样本生成对应于不同的微分方程求解器。具体而言,对于DDPM, Song等指出其反向过程的采样对应于扩散SDE的最大似然SDE求解器,Bao等给出了该过程最优方差的解析形式。对于DDIM, Song等首先说明了其迭代采样与求解ODE之间的相似性。Salimans和Ho指出,采样对应于经过一定变换的扩散ODE的一阶ODE求解器。Lu等人证明了 DDIM 是基于具有半线性结构的扩散ODE的一阶ODE求解器,并给出了相应的高阶求解器的解析解。
2.4、条件DPMs
DDIM 提供了一种通过噪声隐藏变量的确定性抽样进行条件生成的方法,基于分数的 SDE 指出,通过求解条件反向时间 SDE 可以实现条件生成,并提供了三个可控生成的例子,开启了条件生成的研究。
条件 DPMs 提出训练一个噪声图像分类器 q ( y ∣ x t ) {q(y|x_t)} q(y∣xt) 来控制基于类别 y {y} y 的样本生成,梯度 ∇ x t log q ( y ∣ x t ) {{\nabla _{x_t}}\log q(y|x_t)} ∇xtlogq(y∣xt) 的强度为 γ {γ} γ。相比之下,作者在[29]中强调,通过在扩散概率模型的训练中引入条件 y {y} y 可以实现类别引导,这是一种隐式构建分类器的方法,可以采用条件和扰动图像的数据对。此外,最近的工作扩展了类别条件,包括图像、文本和多模态条件生成。
作为条件生成的另一种代表性方法,潜扩散概率模型(Latent Diffusion Probabilistic Models, LDMs)考虑构建预训练的编码器-解码器,并使用 DPMs 在 bottleneck 生成隐变量,这降低了 DPMs 的计算复杂度,使潜空间中的条件操作成为可能。
3、MRI的应用
3.1、重建(Reconstruction)
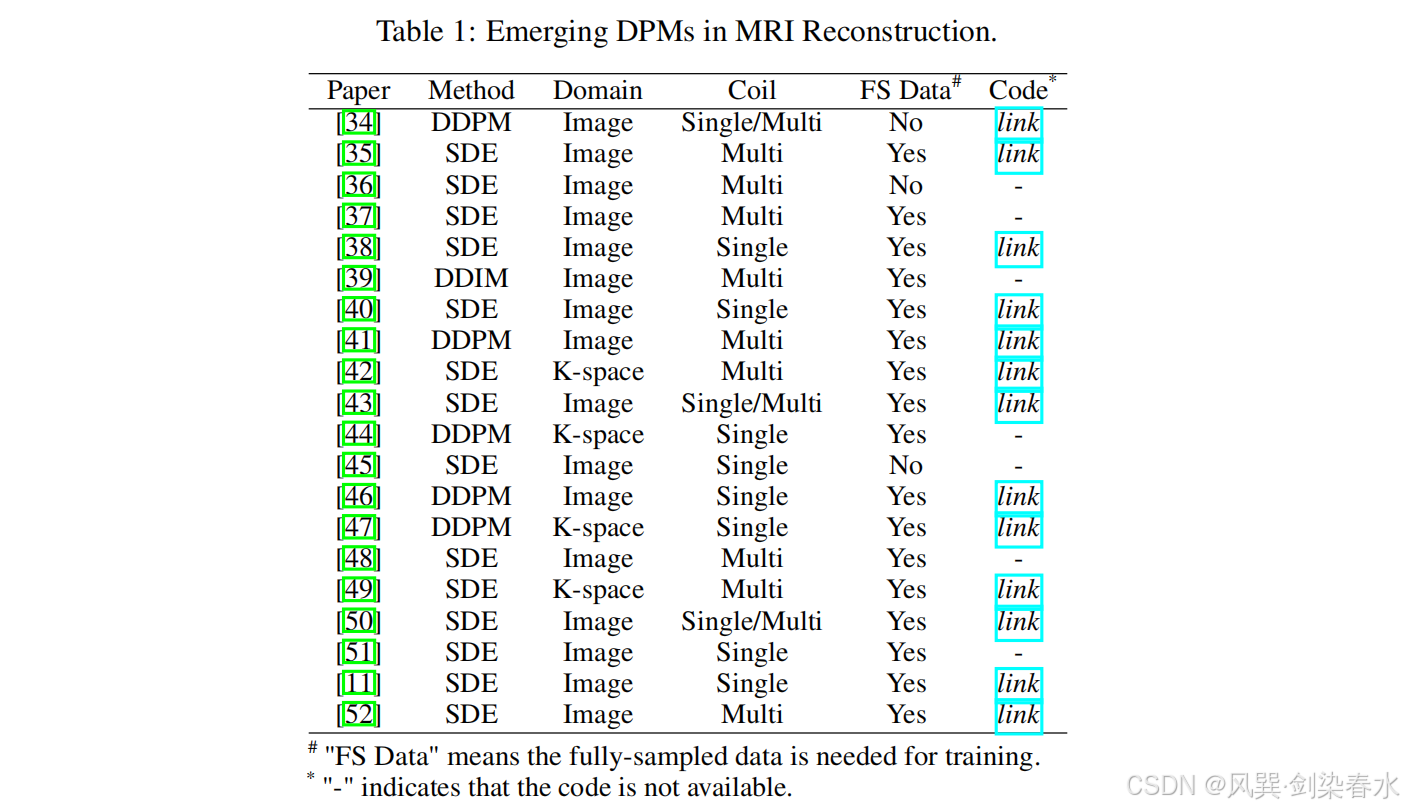
MRI 加速是一个热门的研究课题,它涉及重建欠采样数据以去除伪影。数据驱动的深度学习方法在 MRI 重建中取得了巨大的成功,这些方法大多基于卷积神经网络,需要大量样本进行训练。DPMs 具有较好的重建质量和泛化能力,在解决 MRI 重建逆问题方面显示出潜力。表1列出了采用 DPM 进行 MRI 重建的研究,包括所采用的 DPM、应用DPM的数据域、单线圈或多线圈数据、是否需要全采样数据,以及代码链接。
表1:MRI重建中的DPMs
正向MR采集模型可表示为:
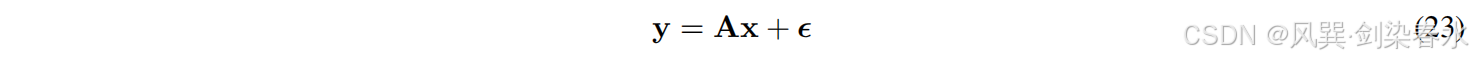
式中,
y
{y}
y 为获取的 k-空间数据,
x
{x}
x 为成像对象,A = MFS 为编码算子,M 为欠采样掩模,F 表示傅里叶变换,S 表示线圈灵敏度图,
ϵ
∼
N
(
0
,
σ
ϵ
2
I
)
{ϵ∼\mathcal{N}(0,σ_ϵ^2 I)}
ϵ∼N(0,σϵ2I) 为采集噪声,从欠采样k-空间数据
y
{y}
y 重建 MR 图像通常被表述为优化以下问题:
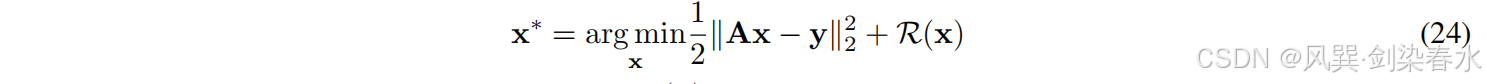
其中第一项加强了数据一致性,
R
(
x
)
{\mathcal{R}(x)}
R(x) 是稳定解的正则化项。
基于 Score 的 SDE 框架,可以通过反向时间 SDE 作为等式从后验分布中采样MR图像,如等式(25),这不同于传统的直接将
x
{x}
x 的先验信息建模为等式(24)。
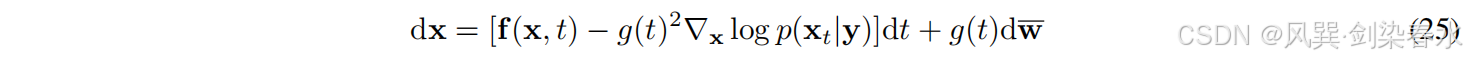
根据贝叶斯规则,我们有:
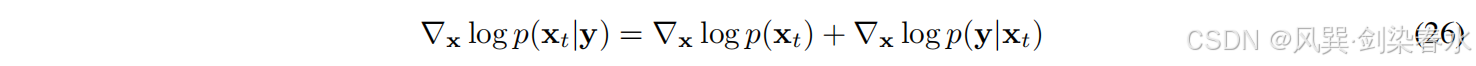
等式(26)中的第一项是先验分布的分数函数,可以通过分数匹配来估计。第二项是似然,它没有封闭形式的解,因为
y
{y}
y 对
x
t
{x_t}
xt 没有显式的依赖。
有不同的方法可以来近似似然项。Jalal等人[52]提出了利用一种近似值的方法: ∇ x log p ( y ∣ x t ) ≈ A H ( y − A x t ) σ ϵ 2 {{\nabla _{x}}\log p(y|x_t)≈\frac{{{A^H}(y - A{x_t})}}{{\sigma _ϵ ^2}}} ∇xlogp(y∣xt)≈σϵ2AH(y−Axt),当 ϵ {ϵ} ϵ 为方差为 σ ϵ 2 {{\sigma _ϵ ^2}} σϵ2 的高斯噪声且 t = 0 {t = 0} t=0 时有效。对于更高的噪声扰动水平 t → T {t→T} t→T, ∇ x log p ( y ∣ x t ) ≈ A H ( y − A x t ) σ ϵ 2 + λ ϵ 2 {{\nabla _{x}}\log p(y|x_t)≈\frac{{{A^H}(y - A{x_t})}}{{\sigma _ϵ ^2}+{λ_ϵ ^2}}} ∇xlogp(y∣xt)≈σϵ2+λϵ2AH(y−Axt),其中 { λ } t = 1 T {\{λ\}^T_{t=1}} {λ}t=1T是超参数。
Song等人和Chung等人提出先根据等式(15)进行无条件采样,然后将中间采样结果投影到测量空间,从而对中间生成进行数据一致性处理, x t {x_t} xt:
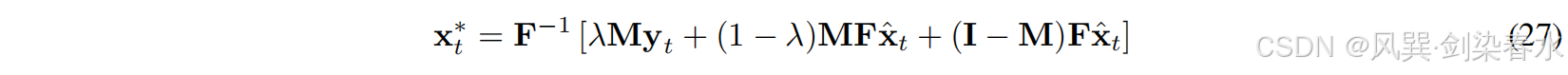
其中,
y
t
{y_t}
yt 为对
y
{y}
y 进行与前向相同的扰动得到的被噪声破坏的采集数据,
x
t
{x_t}
xt 为无条件采样结果,
λ
{λ}
λ 为平衡数据一致性和无条件生成的超参数。图3(a)说明了等式(27)中的数据一致性。
图3:在MRI重建的反向扩散过程中实现条件采样的两种不同方法
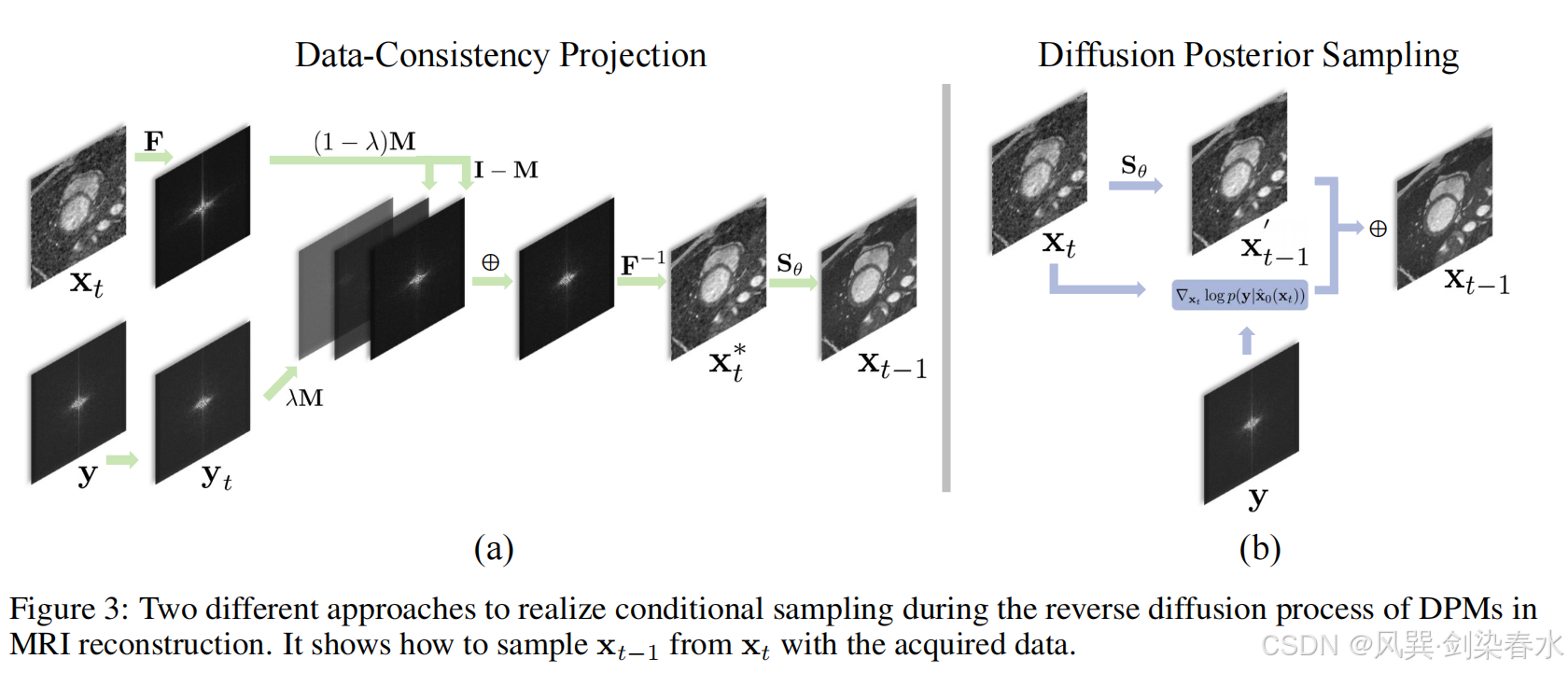
此外,Chung等人利用Tweedie规则的结果,提出了扩散后验抽样(Diffusion Posterior Sampling, DPS)来近似 ∇ x log p ( x t ∣ y ) {{\nabla _{x}}\log p(x_t|y)} ∇xlogp(xt∣y) ,对于VE-DPMs的情况, p 0 t ( x t ∣ x 0 ) = N ( x t ; x 0 , σ t 2 I ) {p_{0t} (x_t|x_0)=\mathcal{N}(x_t;x_0,σ_t^2 I)} p0t(xt∣x0)=N(xt;x0,σt2I) ,可以得到后验期望的封闭式表达式:
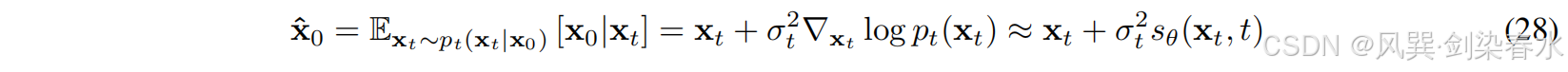
等式(28)表示后验的期望可以用训练好的基于分数的模型
s
θ
(
x
t
,
t
)
{s_θ(x_t, t)}
sθ(xt,t) 来近似。因此,似然项可以近似为
∇
x
log
p
(
y
∣
x
t
)
≈
∇
x
log
p
(
y
∣
x
^
0
(
x
t
)
)
{{\nabla _{x}}\log p(y|x_t)≈{\nabla _{x}}\log p(y|\hat x_0(x_t))}
∇xlogp(y∣xt)≈∇xlogp(y∣x^0(xt)) 。利用图3(b)中的 DPS 近似,等式(25)可用于重建MR图像。
基于 DPMs 的 MRI 重建方法一般可以根据所应用的领域(图像域或k空间)进行分类,下面将分别介绍:
(1)图像域中的DPMs
大多数 DPMs 应用于图像领域的 MRI 重建。Jalal等人[52]首先提出在MR图像上训练基于分数的模型作为 MRI 重建的先验,该模型通过 Langevin 动态后验采样生成高质量的图像,与端到端监督学习方法相比表现出优越的性能。此外,Luo等人[43]更详细地分析了 DPMs 用于重建 MR 图像的鲁棒性和灵活性,阐明了重建的不确定性和计算负担。
为了实现条件生成,Chung等人[50]提出了给定测量值的条件采样方法,该方法在采样过程中增加了预测器和校正器之间的一致性映射。他们的方法也可以应用于多线圈k空间数据,通过分别重建每个线圈图像,然后进行线圈的平方和组合。
Song等人[11]在全采样图像上训练了一个基于分数的模型来捕获先验分布,并提供了如何将获得的测量值和已知的物理模型纳入无条件采样过程的详细数学描述。基本思想是在每个扩散时间步对无条件采样图像进行投影,使其与
y
t
{y_t}
yt 一致,如式(27)所示。
Peng等[46]采用在采样阶段增加数据一致性投影,同时缩短重构时间的思路,在每个扩散时间步平均多次重构,避免缩短采样时间导致重构质量下降。
Güngör等人[41]提出了 AdaDiff 算法,该算法采用大步长加速采样过程,生成初始重构,并在自适应阶段通过与参考数据的对比对重构结果进行细化。
与上述在正向扩散过程中使用全采样图像的工作不同,最近有研究证明了仅使用欠采样 MR 图像训练 MRI 重建 DPMs 的可行性。
Cui等[45]利用贝叶斯神经网络从欠采样图像中学习先验数据分布,然后对分布进行扰动,训练基于分数的模型重建MR图像。
Aali等[36]将 Stein 的无偏风险估计与去噪的分数匹配相结合,提出了一种新的损失函数来训练基于分数的模型。该方法能够对受高斯噪声干扰的数据进行联合去噪,并训练基于分数的模型。
Korkmaz等[34]采用k空间 masking 策略对 DPMs 进行自监督学习,将欠采样k空间数据随机分成两部分,分别用于数据一致性和计算重建损失。此外,本工作还设计了一个展开式 transformer 网络来取代常用的去噪U-Net,它由一个映射器网络和一个展开式去噪模块组成。利用映射器网络捕获从欠采样图像中提取的时间编码信息和先验信息。采用去噪块进行图像去噪和数据一致性处理。
除了直接从欠采样数据中学习外, DPMs 用于 MRI 重建的最新进展还侧重于改进 SDE 的正向和反向过程。
Cao等[48]提出 HFS-SDE,通过将扩散过程限制在高频区域,实现更稳定、更快的 MRI 重建。Cao等[54]和Cui等[37]采用平行成像MRI重构方法 SPIRiT[55] 中自一致项的梯度代替原 SDE 中的漂移系数,强化了扩散系数高斯噪声的自一致特性,为多线圈重构的 SDE 设计提出了新的范式。
Ravula等人[35]没有使用反向 SDE 来重建 MR 图像,而是尝试优化由具有可学习参数的伯努利分布描述的欠采样模式。优化是通过最小化全采样信号和由一个基于相应的欠采样信号的分数估计器产生的结果之间的误差来进行的。此外,DPMs 是专门为 3D MRI 重建而设计的。
Chung等人[40]提出了 DiffusionMBIR,其中使用二维 DPM 进行逐片重建,然后沿切片方向添加经典的总方差先验,增强了切片重建之间的内在一致性。此外,Lee等人[38]提出利用两个垂直的预训练 2D DPM 来增强对 3D 先验分布的利用。
(2)k空间中的DPMs
在应用于k空间域的 MRI 重建 DPMs 中,最具代表性的是MC-DDPM[47]和CDPM[44]。
MC-DDPM定义了k空间中的扩散过程,并将条件分布添加到欠采样掩模中。因此,该方法使用测量先验来确保采样过程中数据的一致性。此外,该方法还可以对采样结果的不确定度进行评估。
CDPM利用欠采样掩模和观测到的k空间数据作为前向马尔可夫链的条件,在此基础上学习到未获取的k空间数据的分布。
Tu等人[49]提出WKGM通过对初始k空间数据进行加权来实现k空间的多线圈重建,以提升高频,抑制低频数据。这种加权的优点是可以减小k空间幅度的动态范围,从而可以很好地捕获先验分布。
3.2、图像生成(Image Generation)
由于DPMs可以稳定地生成具有特定数据结构和病理特征的MRI图像,因此DPMs也为其提供了一种新的数据增强方法,有助于解决下游诊断模型中MRI数据集稀缺的局限性。
具体而言,如何利用 DPMs 处理复杂的数据格式,包括但不限于2D、3D和时空数据,以及如何识别和应用有意义的先验,以获得符合实际要求的样本,是 DPMs 在 MRI 图像生成中需要解决的主要问题。
表2总结了相关工作,包括所采用的DPM、目标器官、与方法相关的数据维度和生成条件、本文中讨论的方法的具体任务及其潜在应用,以及代码链接。
表2:MRI生成中的DPMs
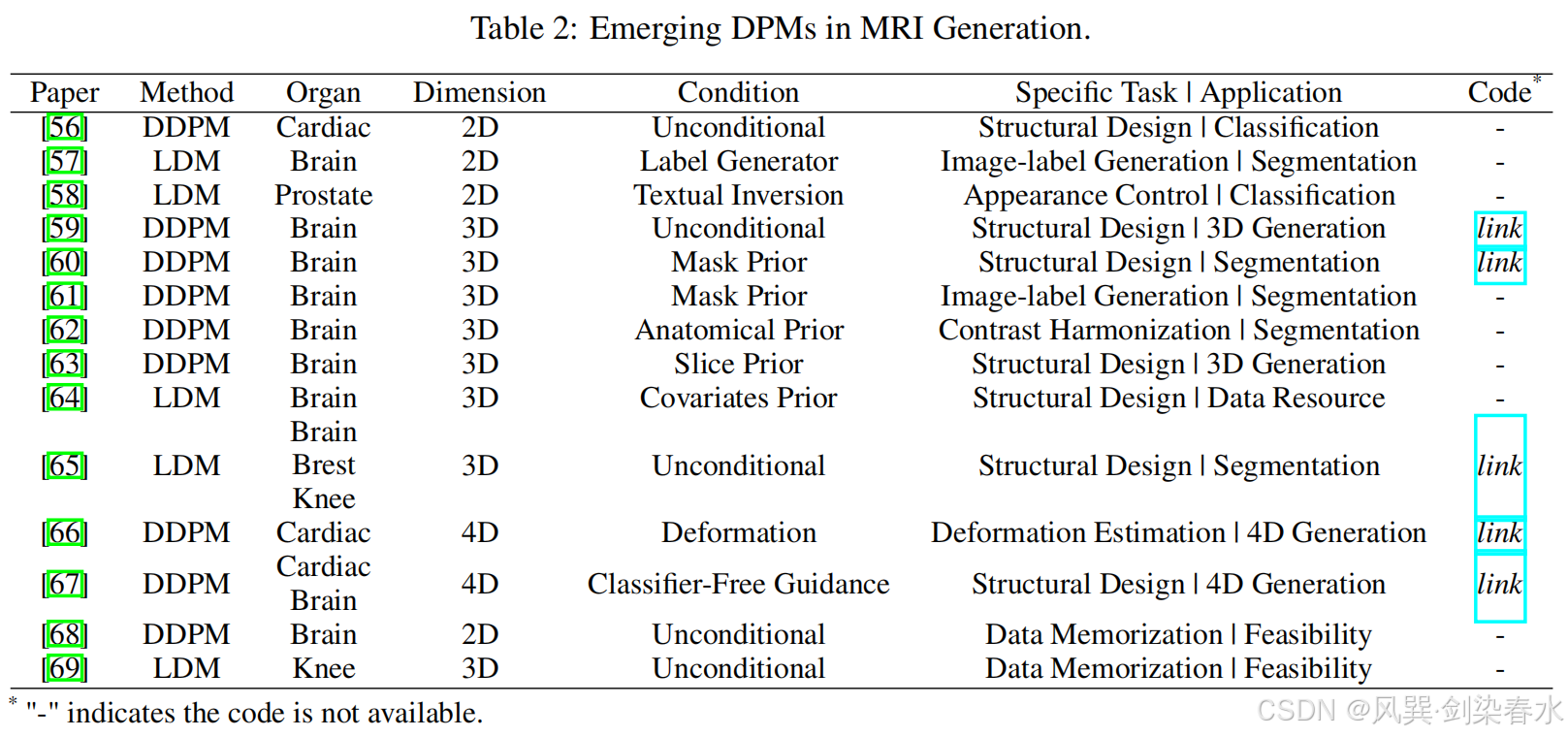
由于早期 DPMs 的计算成本很高,它们在MR图像生成中的应用最初是从2D MRI开始的。这些工作主要集中在优化噪声估计器的结构,结合产生的引导机制,并探索其在下游任务中的潜在应用。
Pan等人[56]提出使用 Swin-vision transformer 作为 DDPM 的噪声估计器来捕获噪声隐变量的局部和全局信息,其中包含丰富的实验设置细节,并进一步讨论了生成的数据在分类任务中的作用。(修改网络结构)
LDMs 的发展为二维MRI数据的生成带来了新的活力。为了改进分割模型的训练,Fernandez等人[57]提出了brainSPADE,该方法基于LDMs,由合成标签生成器和基于编码器-解码器的语义图像生成器组成。(同时生成图像和分割标签)
此外,[58]中的研究讨论了微调自然图像训练的LDM用于医学成像应用的可行性。这项工作的创新之处在于使用文本反转来控制LDM潜在空间中变量的强度。结合代表不同疾病的隐状态,它能够生成具有不同类型疾病和严重程度的不同样本,并展示了通过操纵分割掩码来控制病变外观的潜力。
在将LDMs应用于三维MRI生成之前,DPMs经常被用来解决三维生成问题,首先生成2D子切片,然后将其组装成一个三维体积(3D volume)。Dorjsembe等人[59]首次报道了采用 3D DDPM 将所有2D操作替换为3D操作来生成3D脑MR图像。Dorjsembe等人[60]随后引入了一种基于3D DDPM的方法,在给定分割掩码的条件下合成体积,也证明了该方法在提高分割模型性能方面的有效性。
然而,他们仍然面临着计算成本昂贵的3D操作的挑战。因此,Han等[61]将三维体积数据表示为二维序列,利用MC-DPM生成符合解剖几何的掩模序列,然后设计条件生成器合成与该掩模序列相对应的三维MRI图像。
Durrer等人[62]以2D亚切片的方式将DDPM应用于具有扫描仪固有差异的配对3D MRI数据集,生成的图像保留了解剖信息,但调整了对比度,从而通过将图像映射到相同的目标对比度,增加了不同对比度扫描之间的可比性。
为了增强生成的3D脑MRI的层间依赖性,Peng等人[63]设计了一种策略,在DPM中使用逐片掩模计算MRI体积生成的注意权重。
采用二维亚切片操作的三维MRI生成方法虽然降低了空间复杂度,但却延长了生成时间。此外,当不恰当地使用小数据样本进行训练时,这些方法可能会产生生成伪影和对比度变化。LDMs为三维MRI的可控生成提供了另一种方法。
Pinaya等人[64]使用LDMs创建成人大脑的3D合成MRI图像,并利用交叉注意机制纳入协变量(如年龄、性别和脑容量),使生成符合预期的表征。
根据LDMs的思想,Khader等人[65]使用预先训练的VQ-GAN将图像编码到一个低维的潜在空间,并在潜在表示上构建一个DDPM来生成3D样本,生成结果也被用于训练一个分割网络。
将DPMs应用于高维MRI的生成,如动态MRI仍然是一个需要解决的前沿问题。在这方面有一些开创性的研究。Kim等人[66]将DPMs与传统的可变形深度学习模型相结合,生成心脏电影MRI的中间帧。
此外,为了在多帧心脏MRI和纵向脑MRI的DPMs生成中增加时间依赖性,Yoon等人[67]引入了一种序列感知转换器,可以将时间信息结合到无分类器引导的训练中,从而便于纵向研究中缺失帧和未来图像的生成。
DPMs用于MRI生成的一个关键挑战在于,由DPMs生成的样本是否有利于下游任务。Akbar等人[68]认为常用的指标如FID和IS不足以判断DPMs生成的结果是否与训练数据重复。因此,本研究探讨了DPMs对脑肿瘤MR图像的合成能力,并得出DPMs比GAN更容易记忆训练图像的结论,特别是在小规模的训练数据集上。
作为进一步的研究,Dar等人[69]基于对比学习方法构建了一个自监督模型,比较了生成样本和训练样本的低维潜在表征。本研究也得出了类似的结论,即DPMs可能会记忆训练数据。
3.3、图像转译(Image Translation)
图像转译作为探索MRI、CT和PET等医学图像模式之间关系的一种有效方法,可以丰富下游医学图像分析任务中可用的成像模式。然而,由于获取不同模态图像的高成本和不同模态信号之间复杂的非线性关系,建立生成模型来实现医学图像转译仍然是一个挑战。
近年来,由于 DPMs 中跨域表示的原理和方法的进步,DPMs在MRI图像转译中的应用受到越来越多的关注。表3总结了DPM在MRI翻译中的相关工作,包括所采用的DPM、目标器官、源模式和目标模式、转译任务的类型、模型训练是否需要成对数据以及代码链接。
表3:MRI图像转译中的DPMs
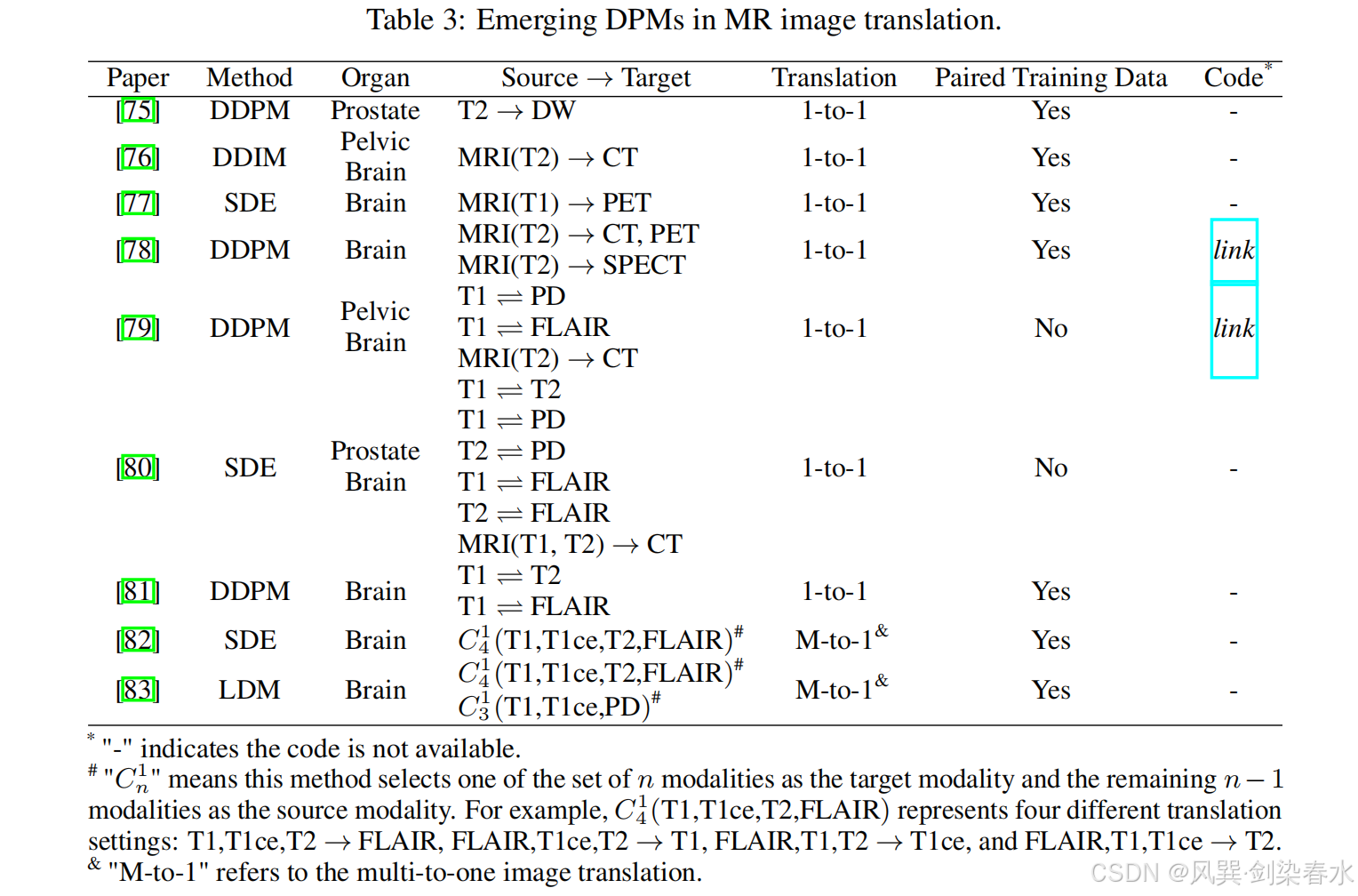
与图4中有条件和无条件的图像生成任务不同,图像转译任务主要是条件生成,目的是了解源模态和目标模态数据分布之间的潜在相关性,从而在给定源模态的情况下生成缺失的模态图像。换言之,图像生成探索一个分布内的条件关系,而转译则侧重于发现不同分布之间的相关性。
图4:DPMs在MR图像生成(a)和图像翻译(b)中的模型设计和常见任务
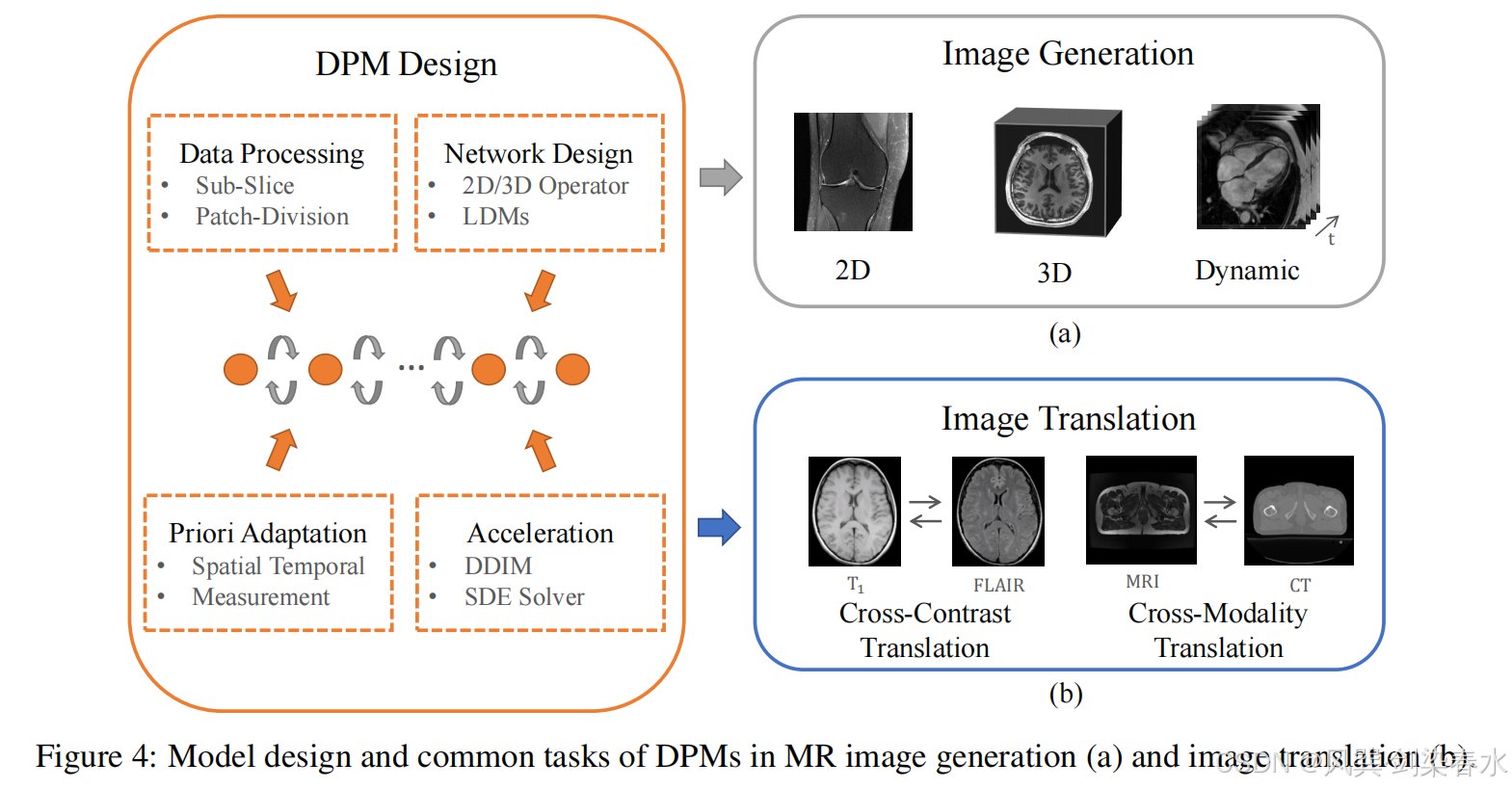
从一对一的图像平移开始,在MR图像转译中应用DPMs的早期尝试是利用来自单一源模态的数据作为采样过程中的一个条件来生成目标模态。一种方法是使用编码器来获得源模态的潜在表示,然后与噪声估计器相结合来实现条件生成。
Saeed等人[75]在合成前列腺弥散加权MR图像时,通过 BERT tokenizer 作为作用于噪声估计器中间层的条件对 t2 加权图像进行编码。
除了潜在表示,原始图像也可以作为生成条件。为了从MR图像中合成高保真CT图像,Li等[76]将MR图像引导的DDIM与采样过程中的Range-Null Space分解CT测量的正则化项结合起来。
近年来的研究对一对一的图像转译DPMs进行了优化。Taofeng等[77]提出利用扩散模型的联合概率分布(JPDDM),以超高场MRI(如5T MRI和7T MRI)为指导,合成脑PET图像。
Zhao等人[78]利用自然图像转译中的EM算法对DDPM的后验采样进行了重新设计,采用无条件生成和条件似然校正,然后将该方法应用于MRI生成CT图像。
此外,为了在未配对的数据集上实现无监督训练,Özbey等人[79]提出了SynDiff,将DPM内的对抗模块合并成一个循环一致的架构,该架构首先使用包含两个生成器-鉴别器对的非扩散模块生成初始转译,然后将初始转译作为生成扩散模块的条件。
作为改进,Wang等人[80]提出了一种名为MIDiffusion的无监督学习方法,利用带有嵌入式调节器的基于分数的SDE,该方法可以利用目标图像和源图像之间的局部互信息来捕获相同的跨模态特征,而无需在域之间直接映射。
尽管通过引入不同的模态条件和优化模型架构,在二维MRI转译方面取得了突出的成就,但将其应用于高维MRI数据还有待广泛研究。Pan等人[81]开发了一种循环引导的DDPM,使用两个3D DDPMs来代表两种不同的MRI对比。交换每个时间步长中的噪声潜在变量作为一个潜在码正则化,以匹配两种MRI模式的生成。虽然这种方法减少了采样过程的不确定性,但如何设计一个更有效的3D MRI转译DPM仍然是一个悬而未决的问题。
与一对一图像转译相比,多对一/多图像转译任务更为复杂,需要特定的模型设计。Meng等人[82]开发了多模态补全框架,其中提出了一个统一的基于多模态条件分数的生成模型,使用多输入多输出条件分数网络生成缺失模态,以学习多模态分布的多模态条件分数。
Jiang等人[83]也提出了一种基于条件LDM的多对一MRI生成模型。该方法采用相似度协同过滤机制,避免了隐空间信息的过度压缩。采用结构引导和自权重自适应策略合成高质量图像。
在潜在空间和领域转译相关的DPM结构中开发更有效的操作,有助于提高复杂MRI转译任务中的模型性能。
3.4、分割(Segmentation)
图像分割是将图像划分为不同的感兴趣区域,是医学图像分析应用的关键步骤。人工分割仍然被认为是临床标准,但需要注意的是,由于经验、专业知识和主观判断的差异,由多个专家进行的注释可能存在显著差异。深度学习方法在医学图像分割任务中取得了最先进的性能。最近的研究也发现,DPMs由于其出色的表现,在这一判别任务中具有潜力。
表4总结了MRI中相关的分割DPMs,其中包括了所采用的DPMs、目标器官、学习策略、不同类型的分割掩模、与该方法相关的条件以及代码链接。具体来说,本文将DPMs的训练是否直接利用每个样本的标注作为学习策略标准。
表4:MRI图像分割中的DPMs
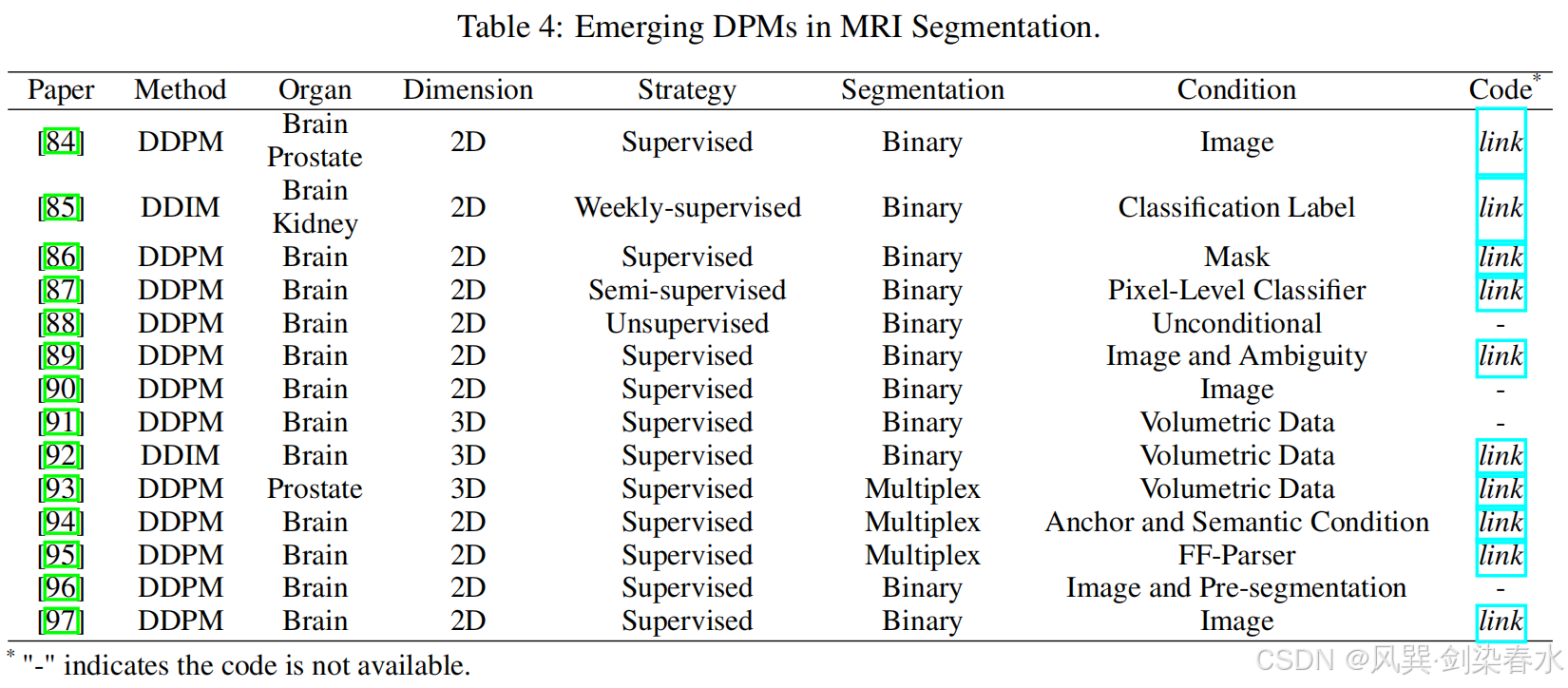
受DPMs在生成语义上有价值的像素级表示方面的显著成功的启发,Wolleb等人[97]首次引入了用于大脑MR图像分割的DDPM。他们提供了一种基于DPMs的图像分割方案,通过合成标记数据,避免了像素级标注的必要性。这种方法虽然具有开创性,但却非常耗时。
Guo等人[96]提出了PD-DDPM,利用预分割结果和基于前向扩散规则的噪声预测来加速分割过程。当与 Attention-Unet 结合时,即使反向采样步骤更少,该方法也优于以前的DDPM。
MedSegDiff [95]通过提出一种动态条件编码策略,改进了医学图像分割的DPM,通过FF-Parser消除了高频噪声分量的负面影响。随后,为了实现噪声和语义特征之间更好的收敛性,他们提出了MedSegDiff-V2 [94],其中使用基于 transformer 的体系结构结合高斯空间注意模块进行噪声估计。
BerDiff模型[90]采用伯努利噪声作为扩散核,提高了DPM对二值图像分割的精度,特别是对离散分割任务。它还可以有效地从反向扩散轨迹中采样子序列,从而加快了分割过程。
由[89]提出的集体智能医学扩散模型引入了一个基于扩散的分割框架,该框架隐式生成了一个分割掩模集合,并提出了一个新的度量,集体洞察评分,用于评估模糊模型的性能。
最近,Amit等人[84]引入了一种新的二值DPM分割,该方法整合了来自多个注释的信息,创建了一个反映共识的统一分割图,提供了一种融合多个专家注释的独特方法。
尽管在二维分割方面取得了上述成就,但 volumetric MRI 还需要基于DPM的分割方法,能够从三维数据中准确提取器官和病变。提出了Diff-UNet [92]进行三维多类分割,采用标签嵌入操作将分割标签映射转换为 one-hot 标签。在测试过程中,它采用了一个基于步进不确定性(step-uncertainty-based)的融合模块,在去噪过程中融合多个预测,以增强分割的鲁棒性。
Fu等人[93]通过解决导致分割性能下降的训练测试不一致性问题,利用DDPM改进了三维多类图像分割问题。观察到在训练期间采用的噪声破坏的 ground-truth mask 可能仍然包含形态特征,导致数据泄漏,作者提出了一个循环训练策略,使用使用前几步的预测而不是噪声破坏的 ground-truth mask 在预测下一步的噪声mask,对齐训练和推理过程。在这项工作中,直接对分割掩模预测,而不是采样噪声,以方便在训练过程中使用常见的Dice损失和交叉熵。
此外,Nichol等人[98]采用了重采样方差调度,实现了训练和推理的五步去噪过程,在很大程度上节省了计算时间和资源。
为了提高基于 DPM 的三维体分割的计算速度和存储效率,Bieder等[91]引入了PatchDDM,该算法在坐标编码的 patch 上进行训练,允许在采样过程中以全分辨率处理大量数据。
Akbar等人[86]探讨了利用合成MRI数据训练脑肿瘤分割模型的可行性。他们将四种模态的肿瘤MR图像加上一个通道的肿瘤标注,输入DDPM和四种GANs模型,以生成带有mask的合成数据。分割结果表明,用合成图像训练的2D-UNet分割模型,获得了与用真实图像训练的分割模型相似的性能指标。与现有的GAN方法相比,DDPM在合成脑肿瘤图像方面取得了具有竞争力的性能,而作者指出,当训练数据集太小时,DDPM比GAN方法更有可能记忆训练图像。
与在训练过程中需要手动标注的监督方法不同,目前的弱监督和半监督分割方法主要将 DPMs作为图像的语义编码器,通过观察这些语义表示的差异来实现像素级分割。例如,[99]的研究利用多层感知器对DDPM的潜在表示进行分类,实现了对自然图像的分割。DPMs作为表示学习者的训练不依赖于注释,标签监督主要用于观察表示之间的差异,消除了费力的案例级注释的要求。
对于MRI的应用,Alshenoudy等人[87]提出了一种在注释样本稀缺的情况下的半监督脑肿瘤分割方法。该分割方法是由[99]的一种方法发展而来的,采用DDPM来学习输入图像的视觉表示,并以无监督的方式进行分割。然而,分割是通过对标记数据上的噪声预测器网络进行微调,而不是使用像素级分类器。
Hu等[85]通过比较不同条件下的采样,创新性地探索了条件 DPMs 对目标对象的定位。此外,为了放大不同条件引起的差异,该方法从DPM预测的与条件相关的噪声梯度中提取了语义信息。在不同的MRI数据集上进行的实验表明,它在脑肿瘤和肾脏分割方面具有很强的性能。
在基于DPMs的分割中,观察表征差异的思想也可以通过设计损失函数来实现。Tursynbek等人[88]设计了一个三维生成DPM,使用U-Net架构作为三维图像的特征提取器,用于无监督分割。该方法采用复合损失增强特征一致性、视觉一致性和光度不变性,在合成和真实获得的脑肿瘤MRI数据集上取得了优越的分割性能。
在未来的应用中,除了探索更多的测量表示差异的方法外,我们还期望有更多的研究集中于使用具有分割相关先验的 DPMs 来提高特征提取的效率和可靠性。此外,弱监督分割 DPMs 在高维MR图像的多标签分割任务中的应用也值得探索。
3.5、异常检测(Anomaly Detection)
与基于 DPMs 的分割方法主要关注生成 mask 不同,异常检测的目的是通过将输入的图像与生成的包含健康组织的图像进行比较来突出异常区域。因此,具有优越生成能力的 DPMs 在异常检测任务中越来越受欢迎。
表5总结了DPM在MR图像异常检测中应用的研究,包括所采用的DPM、目标器官、学习策略、与该方法相关的条件和开放源代码链接。具体来说,本文将 DPM 的训练是否直接利用每个样本的已知异常信息作为学习策略标准。
表5:MRI图像异常检测中的DPMs
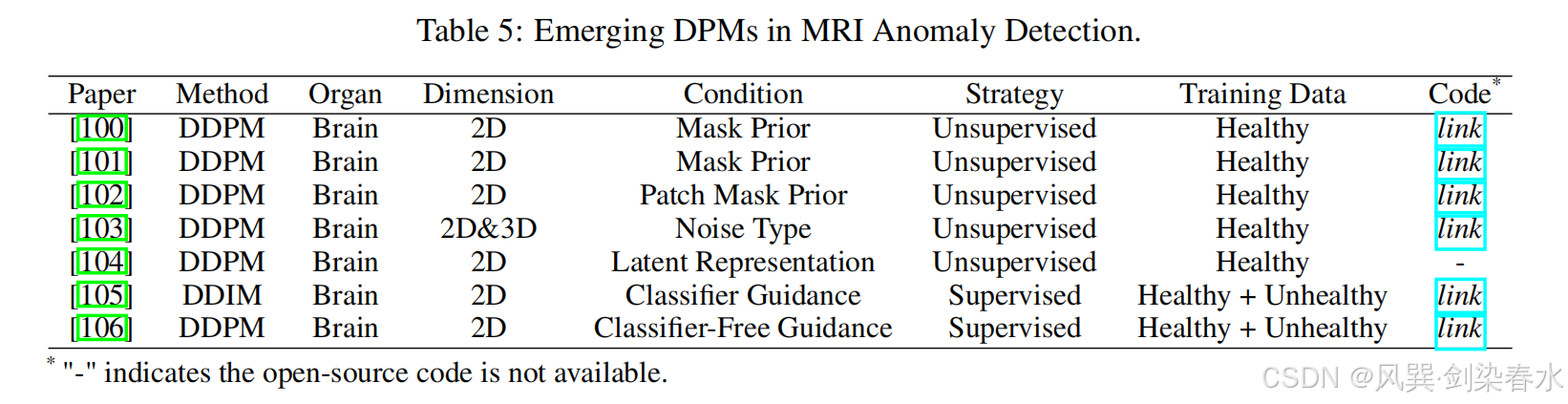
Wolleb等人[105]首先将DPMs应用于MRI异常检测。这项工作在健康和患病受试者的数据集上训练了一个DDPM和一个二元分类器。在推理过程中,将输入图像扰动成一个有噪声的正向DDIM采样图像,然后通过分类器引导的DDIM采样过程生成健康受试者的图像。异常检测是通过计算生成的图像与原始图像的像素级差来实现的。
Sanchees等[106]探索了DPMs对脑损伤的提取。他们发现,只根据健康数据进行训练的DPMs不足以识别大脑损伤。然后,他们实现了一个反事实的DPM,通过隐式引导、条件注意和动态归一化,对给定的输入图像生成健康的反事实,从而使脑病变能够定位。随后,通过比较事实输入图像和反事实输出图像来实现异常检测。
Pinaya等[104]提出了一种采用VQ-VAE和DDPM的无监督异常检测方法。VQ-VAE用于获得输入图像的潜在表示。DDPM学习了健康数据的潜在表示的分布。在推理过程中,通过计算KL散度来评估每个反向步骤与预期高斯转移的接近程度,因此该方法可以通过对KL散度进行阈值化来得到异常的掩模。该设置的主要动机是,如果输入图像来自一个健康的受试者,反向步骤只去除添加的高斯噪声;如果图像包含异常,每个反向步骤也会去除部分异常区域的信号,导致高KL散度。然后在反向过程中使用异常掩模对潜在空间中的异常进行校正,并使用VQ-VAE解码器得到经过异常校正的输出图像。
为了研究噪声在基于去噪模型的异常检测中的作用,在二维头部MRI和三维头部CT数据集上,[103]研究分别使用三种噪声(高斯、Simplex或coarse)比较了经典去噪自编码器和基于DPMs方法。结果表明,噪声类型确实影响了去噪模型的异常检测性能,且coarse噪声的性能优于其他两种噪声类型。关于去噪模型,作者发现具有最优噪声的简单去噪自编码器比更先进的DPMs表现得更好,而DPMs显示了“治愈”异常和产生令人信服的高清重建的能力。
前面提到的用于异常检测的DPMs对整个图像进行了噪声估计。Behrendt等人[102]认为,对整个图像进行噪声估计使得准确地重建大脑的复杂结构变得困难。因此,他们应用[108]中提出的基于补丁的DDPM生成图像patch,并将其拼接在一起,获得最终的健康大脑MR图像,以计算异常评分。
此外,Iqbal等人[101]提出了一种masked-DDPM方法,该方法在输入DDPM进行训练之前,将输入图像在空间图像域和频域进行masking,添加了masking-based的正则化。masking策略对DDPM施加了一个约束,以便在推断过程中生成健康的图像,而不管输入的图像如何。
为了提高DPMs在检测不同类型异常方面的泛化能力,AutoDDPM [100]集成了masking、stitching和resampling操作。具体来说,预先训练的DDPM在自动mask设置下生成伪健康样本,然后在去噪过程中将其缝合到unmasked的原始健康组织上。对联合概念分布的重新采样实现了协调和in-painting效果,产生了高质量的伪健康重建。
3.6、进一步研究的课题(Further Research Topics)
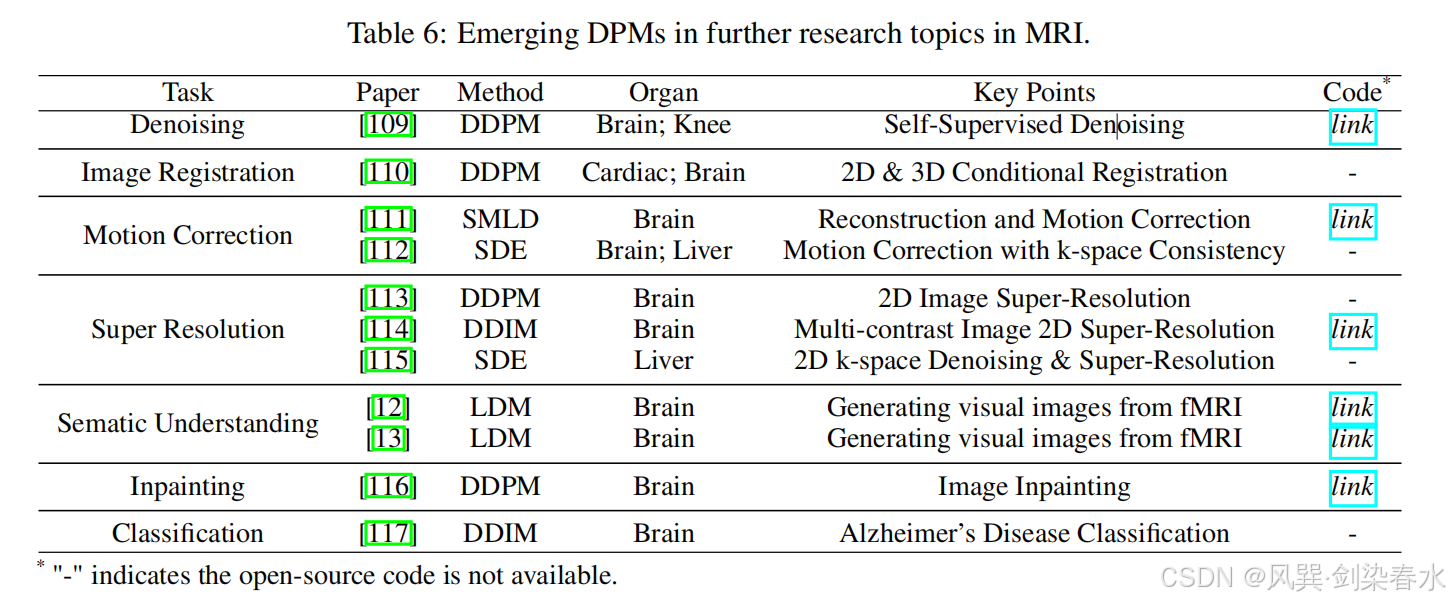
虽然DPMs已经被证明是上述各种MRI任务中有用的工具,但在MRI中还有其他问题可以通过DPMs来解决,这只有一些初步的研究。表6总结了这些方向、所采用的DPM、目标器官、每个研究的重点和开放源代码链接。下面,我们将从两个角度简要介绍这些开创性的研究:成像增强(Imaging Enhancement)和其他任务。
表6:MRI图像新兴应用中的DPMs
3.6.1、成像增强
作为一种使用噪声估计生成图像的一种新兴范例,DPMs最直接的应用之一是去除成像过程中引入的随机噪声。Xiang[109]等人设计了一种基于DDPM的二维和三维扩散加权MRI的自监督去噪方法。最近的研究表明,DPMs在更专业的成像增强主题上具有巨大的潜力,如运动校正、超分辨率和语义理解。
(1)运动校正(Motion Correction)
运动伪影还原是MRI领域的一个活跃研究领域,许多深度学习方法已经被开发出来。然而,这些深度学习方法大多需要配对的无运动和运动损坏图像进行监督训练,这在实践中很难获得。用具有运动伪影的模拟图像训练的模型,可能不能推广到真实的运动伪影。
为了解决这个问题,Levac等人[111]提出了一种方法,可以同时重建欠采样的MR图像,并使用基于分数的DPM来估计刚性头部运动。虽然基于分数的DPM受到模拟运动数据的监督,但它与前向模型(包括采样掩码和运动模式)不可知,使其适用于具有不可预测患者运动的真实MR采集。
最近,Oh等人[112]提出了一种基于退火的分数方法,用于减少腹部MR图像中的呼吸运动伪影。在无运动图像上训练的DPM能够通过使用重复的扩散-反向过程和在反向过程的每一步中添加低频一致性来消除运动伪影。
(2)超分辨率(Super-Resolution)
高分辨率MRI图像有利于描绘精细解剖结构和小病变。然而,由于磁场强度、信噪比和采集时间等限制,获取高分辨率图像具有挑战性。超分辨率旨在从低分辨率输入中恢复高频信息。采用 DPMs 的MRI超分辨率可以在图像域或获得的k空间域。
在图像域中,低分辨率图像通常用作生成高分辨率图像[113]的条件。此外,对于多对比MRI,Mao等人[114]提出了一个将解纠缠 U-Net 主干与 guided-DDIM 相结合的框架,该框架可以利用对比之间的互补信息实现超分辨率。
在k空间域中,Chung等人[115]提出了一种基于分数的SDE来生成高频分量,同时以正则化的方式保留低频信号。
(3)语义理解(Semantic Understanding)
功能磁共振成像(functional magnetic resonance imaging, fMRI)作为反映大脑活动的MRI的一种特殊应用,包含了丰富的与视觉功能相关的信息。有研究探讨 DPMs 是否可以用于挖掘 fMRI 数据中嵌入的视觉语义信息,甚至直接恢复视觉图像。
Chen等人[12]开发了MinD-Vis模型,该模型分为两个主要阶段,以解决从fMRI信号中重建具有正确语义信息的高质量图像的挑战。受初级视觉皮层信息稀疏编码的启发,他们的模型的第一阶段将fMRI数据表示为具有局部约束的稀疏编码表示。然后,在第二阶段使用双条件LDM和端到端微调生成具有编码表示的视觉内容。
Takagi等人[13]结合了他们早期工作的三个进展:从大脑活动中解码文本,使用GAN进行结构图像重建的非线性优化,以及使用LDM从大脑活动中解码深度信息,以生成具有准确语义信息的图像。
3.6.2、其他任务
(1)图像配准(Image Registration)
使用生成式学习的配准算法已被证明在对齐不同的MRI扫描方面是有效的。其基本思想是利用网络获得运动图像和固定图像之间的变形场,然后利用该变形场扭曲运动图像以实现配准。
Kim等人[110]首次报道了使用DPMs进行2D面部表情和3D心脏MRI配准的变形框架。这个框架的一部分是一个扩散网络,它学习运动图像和固定图像之间的运动场的条件分数。该框架的另一部分是变形网络,它可以利用学习到的条件分数来估计变形场并产生变形图像。值得注意的是,学习到的扩散网络的潜在特征包含空间信息,然后可以线性缩放,生成从固定图像到运动图像的连续轨迹的运动场。
(2)图像修补(Inpainting)
对于修复,Rouzrokh等[116]利用DDPM构建了一个二维轴向切片图像修复工具,可以在用户指定区域添加高级别胶质瘤和相应的肿瘤成分或正常脑组织,解决实践中高级别胶质瘤数据不足的问题。
(3)分类(Classification)
在分类方面,Ijishakin等[117]提出利用 DDIM 的潜在编码与类别语义编码器隐变量之间的余弦相似度对阿尔茨海默病进行分类。该方法在提高模型可解释性的同时,取得了与黑盒模型相当的分类性能。
4、趋势与挑战
随着DPMs方法的快速发展和对大型生成模型应用的日益关注,DPMs在不同的MRI任务中显示出了强大的应用潜力。在MRI中,人们希望有高分辨率、无伪影和多对比度的图像来准确诊断。DPM作为一种有效的生成高保真样本的方法,在MR图像重建中取得了显著的性能,比其他任务更受关注,如图1(b)所示。通过在数据中添加噪声和去除噪声以达到所需的数据分布的两个过程,DPMs能够捕获信号和噪声/伪影之间的复杂关系。
Chung等人[50]证明,基于分数的SDE的DPM可以推广到单线圈和多线圈复杂数据,并且对不同的欠采样模式具有鲁棒性,这对于以前的非DPM方法似乎是不可能的。
由于DPM具有条件和无条件生成高质量和高多样性图像的强大能力,因此在MR图像转译和生成中越来越受欢迎。
此外,还观察到DPM可以作为一种有效的表征学习者。由于不需要学习额外的编码器来将图像映射到潜在空间,因此DPM在分割任务中具有独特的优势。
虽然DPMs在一些MRI任务中显示出了巨大的潜力,但通过分析回顾的研究,本文确定了将DPMs应用于MRI的具体趋势和挑战。下面将分享对模型设计和扩展应用研究方向的见解。
4.1、模型设计
(1)加速采样(Accelerated Sampling)
扩散概率模型的一个主要特点是需要大量的步骤来获得高质量的样本。因此,探索有效的采样方法来提高生成速度,有利于DPMs在MRI中的广泛应用。
Yang等[118]总结了DPMs中抽样加速的两种主流方法:无学习抽样和基于学习的抽样。
无学习抽样是一种不需要额外学习就能实现加速抽样的方法。例如,Wizadwongsa等人[119]提供了一种基于算子分裂方法的解决方案来减少采样时间,Lu等人[27]用数据预测模型求解扩散ODE来减小步长。Chung等[39]提出将中间采样结果分解为干净数据流形和噪声数据流形的两个正交部分,并在数据一致性中利用共轭梯度更新,确保中间重构落在干净流形上,实现更准确、更快的重构。
基于学习的采样指的是那些需要在训练DPMs之外学习求解器的方法。例如,Chung等人[51]提出了一个更好的初始化,如预测一些预先训练的神经网络,而不是随机噪声,这可以显著减少采样步数。类似地,Zheng等人[120]设计了一个对抗性自编码器来学习隐式分布以启动反向过程。Luhman等人[121]提出了一种利用知识蒸馏加速图像生成的方法。
(2)高维MRI的应用(Application for High-dimensional MRI)
DPMs 在MRI重建、去噪和超分辨率方面取得了显著的性能。然而,大多数工作在像素空间中训练DPMs,其中每个扩散时间步长的变量与原始数据共享相同的维数。对于具有额外对比度或时间维度的高维MRI数据,如果由 DPMs 单独处理,则不能利用对比度间或时间相关性。如果同时学习,计算负担可能会显著增加,因为 DPMs 不会减少数据维度。
LDMs 可以在一个更低维的潜空间而不是像素空间中工作,这可能提供了一个可行的解决方案。在 LDMs 中,利用变分自编码器,其中编码器将数据压缩到潜空间,然后在潜空间中应用 DPMs,之后,解码器将扩散代从潜空间映射到数据空间。然而,将 LDMs 应用于 MRI 重建可能具有挑战性,因为很难保证数据在潜在空间中保持数据的一致性。
Song等人[122]最近提出了一种算法,通过解决反向采样过程中的一个优化问题来增强数据的一致性,之后设计了一种新的重采样方案,将测量一致的样本映射回正确的数据流形上。该方法可以很好地解决线性和非线性逆问题,并为其在高维MRI中的应用提供了一个很有前途的范例。
(3)联合先验(Incorporating Prior)
在 DPMs 的噪声估计和采样中加入MRI先验是降低生成MRI数据随机性的常用方法。具体来说,在逆向过程的采样过程中,通常通过数据一致性约束加入观测模式(observation patterns)、掩码标签(mask labels)等先验信息。
另一种方法将先验信息纳入学习参数,如特定的评分设计和基于测量模态的条件生成。MRI提供了丰富的物理先验,可用于指导模型训练。
最近的工作,已经开始研究将MRI物理模型纳入 DPMs 的设计。设计包含相关MRI先验的DPMs是提高DPMs生成质量的一个很有前途的方向。
(4)更多的比较研究(More Comparative Studies)
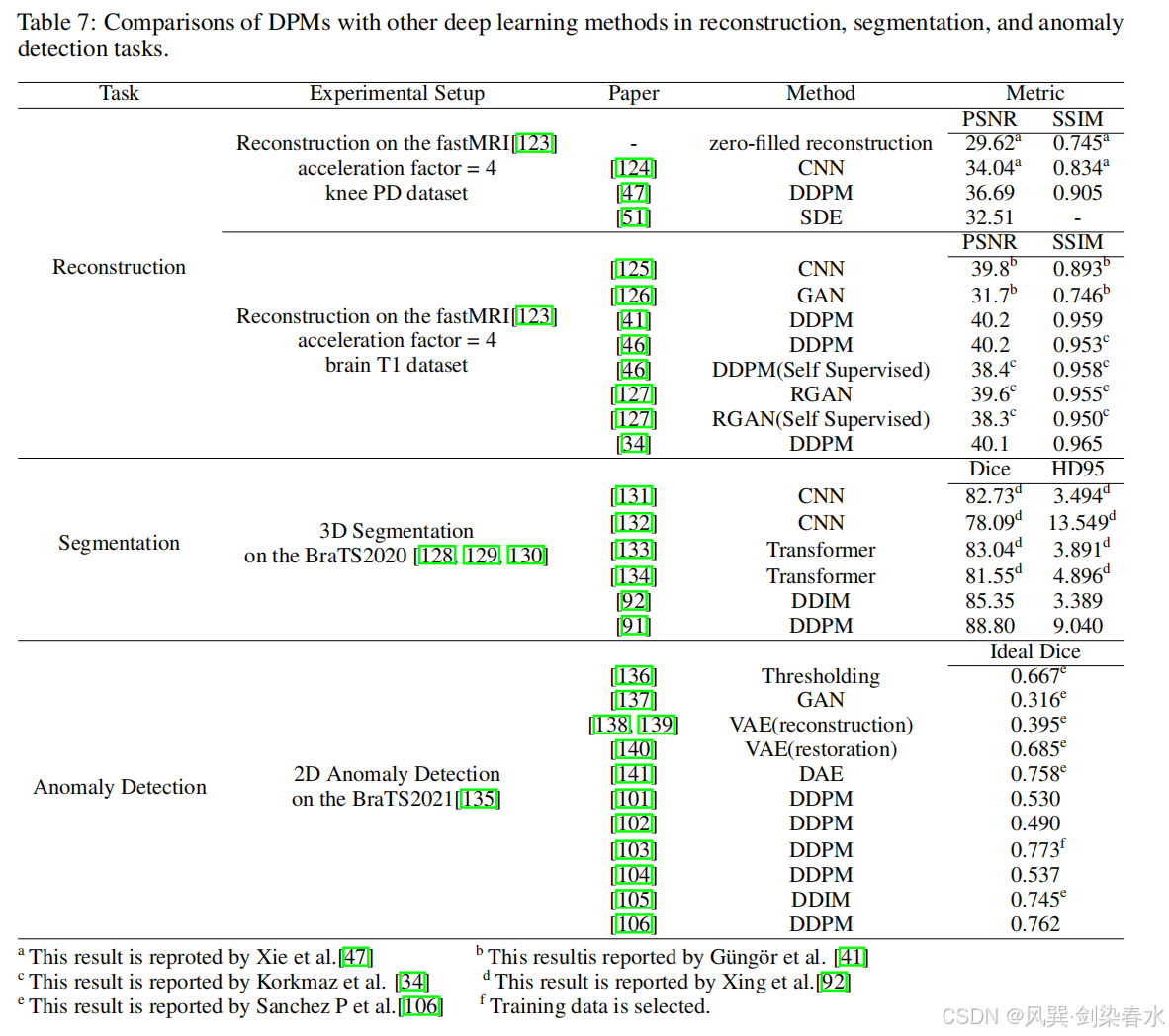
DPMs已经证明了它们在各种MRI任务中的方法创新方面的潜力。在两个重建研究中,一个分割和一个异常检测实验中,如表7所示,与其他著名方法的评估结果表明,DPMs在这些MRI任务中具有出色的表现。
然而,我们注意到 DPMs 在MRI中的应用仍处于早期阶段,在公共数据集中报告的比较结果可能不会收集用于所有相关任务。对于 DPMs 在MRI中的广泛应用,它们与其他深度学习方法的公平比较是必要的,用于各种MRI任务。
表7:DPMs与其他深度学习方法在重建、分割和异常检测任务中的比较
4.2、扩展应用
(1)器官与任务(Organ & Tasks)
DPMs 已经展示了准确描绘数据分布和可控地生成高质量样本的强大功能。然而,训练具有这些能力的DPM通常需要大量高质量的MRI样本。由于获取MRI数据相对昂贵,数据丰富度仍然是 DPMs 在MRI中应用的重大挑战之一。
显然,不同MRI应用场景中的数据可用性直接影响了DPMs所关注的器官。从DPMs在MRI中的不同应用表中总结的器官,如图5可以看出,关注大脑的研究数量很大程度上超过了其他器官,这是因为有丰富的大脑MRI公共数据集。
图5:DPMs在不同MRI应用中所考虑的器官
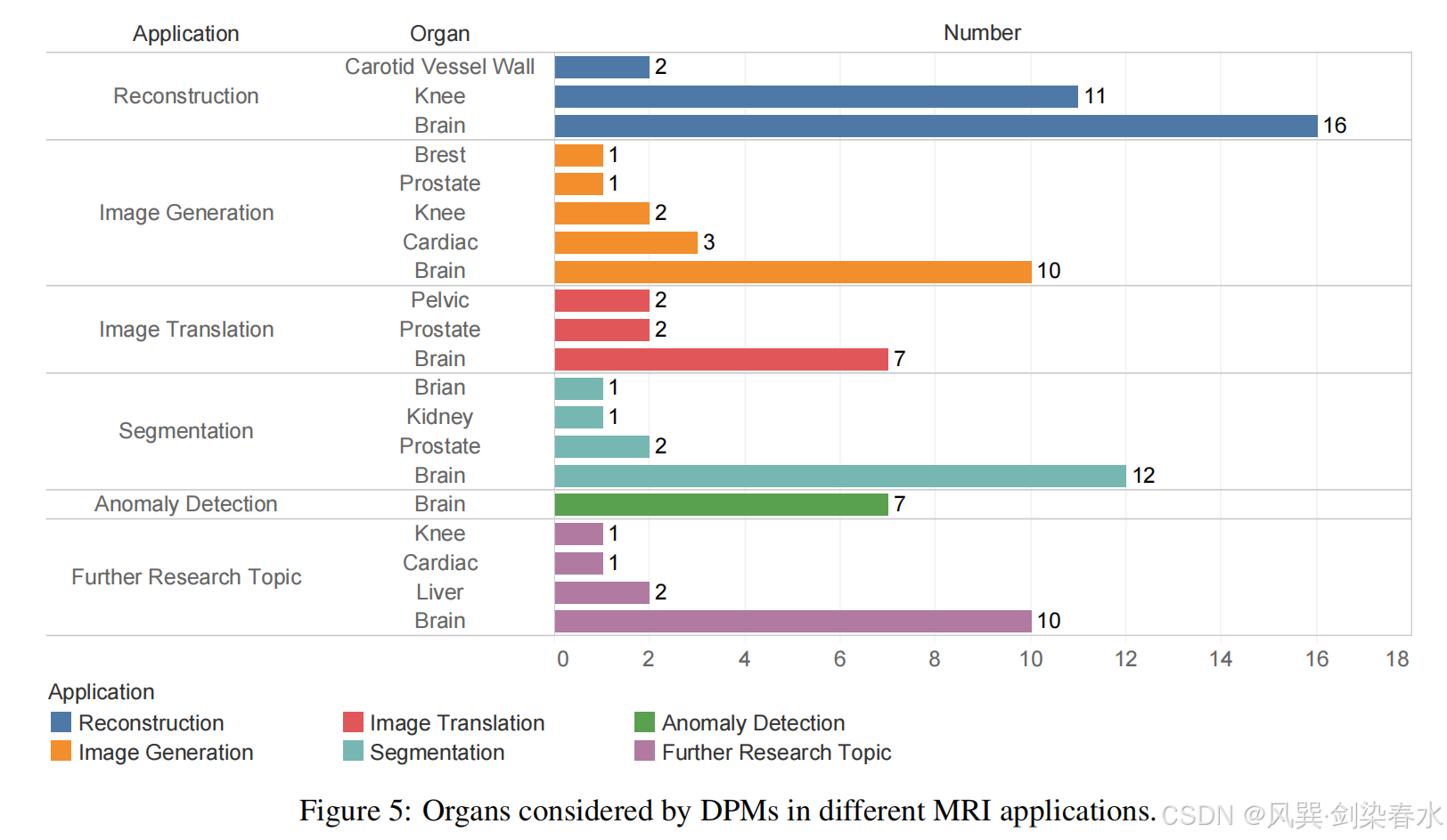
表8总结了在 DPMs 中采用的公共MRI数据集。相比之下,DPMs在胸椎和腹部区域,如心脏、肾脏和前列腺的应用报道较少。可能的原因是,这些身体部位的可用数据集稀缺,与这些区域相关的一些应用更具挑战性,可能需要进一步开发 DPMs。
表8:DPMs中常用的公共MRI数据集
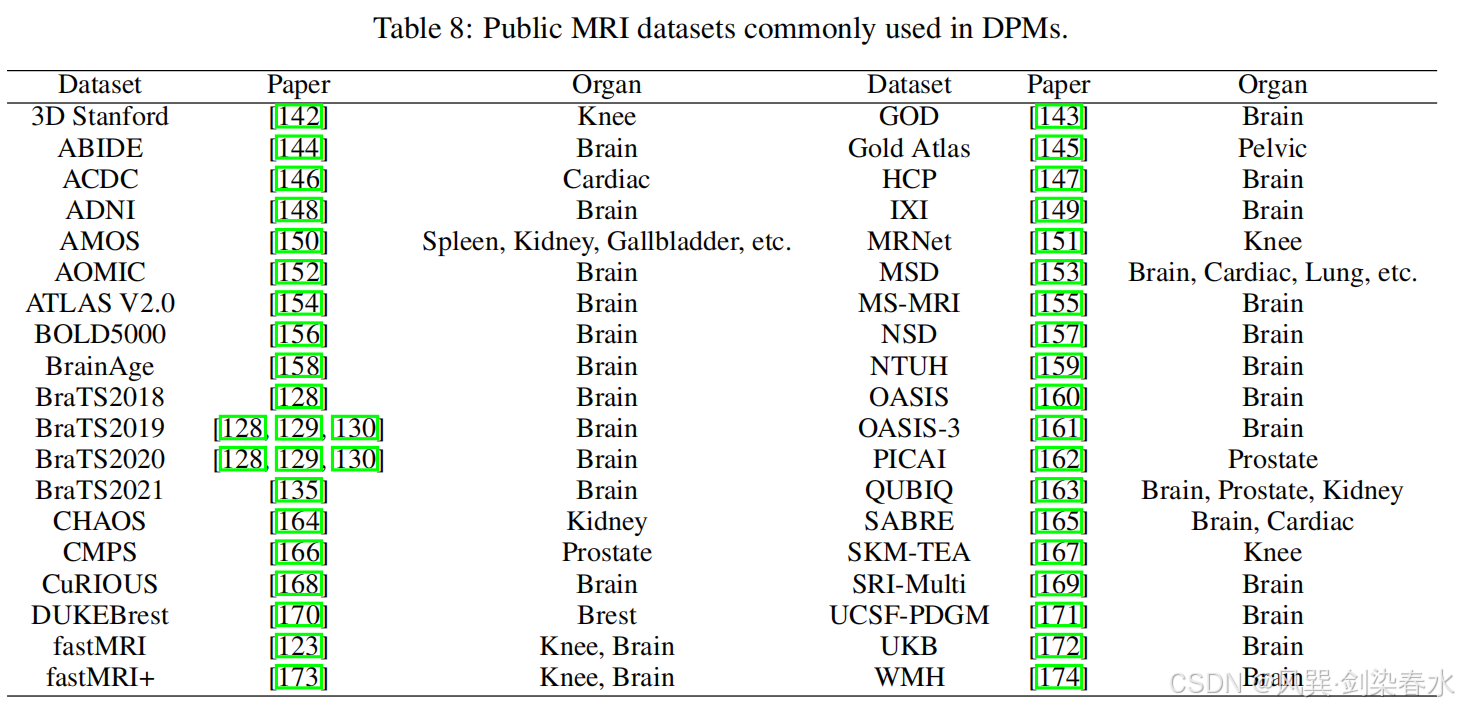
虽然研究较少,但胸腹MRI由于其独特的生理特征和获取挑战,对 DPMs 具有巨大的潜力。例如,为了减轻呼吸和心脏运动,所获得的心脏图像的覆盖范围和空间分辨率通常会在一段合理的扫描时间内受到损害,此时 DPMs 可用于提高心脏图像的重建质量和分辨率。
此外,在腹部和心脏的MRI图像中往往存在运动伪影。以往基于深度学习的运动伪影减少方法的一个基本挑战是,模型训练需要配对的无运动和运动损坏图像,这可能难以获取或模拟。DPMs 的主要优势之一是能够在没有成对标签数据的情况下工作。
[112]的研究表明,仅用无运动图像训练的基于分数的方法可以有效地减少反向扩散过程中的运动伪影,并且优于基于GAN的方法。因此,DPMs 在MRI运动伪影减少方面的潜力值得进一步探索。
总而言之,我们注意到,需要高质量和多样化的公开可用的MRI数据集,以促进在更多的MRI任务中探索DPMs。
(2)隐私保护(Privacy Protection)
尽管 DPMs 在许多应用场景中都表现出优于其他生成模型的优势,但必须承认,由于 DPMs 采用了与训练数据分布相反的生成过程,因此与其他生成模型相比,DPMs 可能会增加患者隐私泄露的风险。
因此,在训练和应用阶段保护患者的隐私对于广泛利用 DPMs 进行临床应用至关重要。在自然图像中已经有了一些新兴的解决方案。在训练阶段,Dockhorn等人[176]提出了一种方法,将严格的差异隐私结合到 DPMs 的训练中,以确保生成的结果是否来自训练数据。此外,[177]将对抗性语义编码纳入DDIM,并应用语义正则化,对最终图像添加难以察觉的语义扰动,从而隐式地保护训练数据中的身份隐私。
在应用阶段,DPMs与联邦学习的结合也在[178]和[179]等工作中出现,这不仅减轻了DPMs繁重的计算问题,也使应用DPMs更有利于隐私性成为可能。所有这些工作都为加强对MRI数据中患者隐私的保护提供了很有前途的解决方案。
(3)值得信赖的DPMs(Trustworthy DPMs)
DPMs 及其在包括MRI在内的医学成像方面的应用仍处于早期阶段。现有的绝大多数关于 DPMs 的研究都集中在技术的发展上。只有少数研究涉及到 DPM 评估中的临床评估。
Khader等人[65]利用了两位经验丰富的放射科医生的定量评估来评估所开发的 DPM 模型的合成能力。Saeed等人[75]由泌尿外科专家评估产生的病理。进一步研究基于 DPM 的方法在不同MRI任务中的临床应用具有重要价值。
在可信人工智能的背景下,在 MRI 中构建一个可信的 DPM 对其临床采用至关重要,其关键在于生成结果的稳定性和可靠性。除了设计符合临床要求的评估指标和生成结果的不确定性度量作为 DPMs 的先验或有条件指导外,对 DPMs 主干的对抗性攻击的研究还可以为在MRI中构建稳健和可信的 DPMs 提供新的思路。目前的工作,如[180]和[181],已经研究了在自然图像中,甚至在医学图像中对 DPMs 的对抗性攻击。针对临床应用,本文设想在不久的将来将会有更多的研究,在医学成像中构建值得信赖的 DPMs 。
5、结论
本文对DPMs在各种MRI任务中的应用进行了全面和及时的综述。为了帮助研究人员了解 DPMs 的基本原理,首先从扩散正向过程和反向过程的统一角度介绍了两种主要的 DPMs,并总结了当前条件 DPMs 的发展。接下来,回顾了 DPMs 在各种 MRI 任务中的研究,包括重建、图像生成和转译、分割、异常检测等开创性研究课题,旨在帮助研究人员根据实际需要找到最新的文献。对于每个任务,除了介绍相关工作外,还提供了一个表,其中包含已采用的 DPM、目标器官、任务相关关键点和可用的开放源代码链接,可以为有兴趣采用 DPM 的研究人员提供有用的参考和来源。此外,还指出了在 MRI 中应用 DPMs 的挑战和未来的发展方向,研究人员可以从模型设计、数据资源和评估方法的实际见解中获益。由于 MRI 中的 DPMs 发展迅速,本综述可能没有涵盖所有的研究。然而,本文不遗余力地收集了相关的和高质量的论文。我们相信,本文对 MRI 中 DPMs 的深刻见解可以为对这一领域感兴趣的研究人员提供很好的参考,并有助于进一步的发展。
完结撒花~

评论记录:
回复评论: