VS Code Java 开发指南！

640?wx_fmt=gif

本文是一份提供给 Java 开发人员在 2019 年使用 Visual Studio Code 的终极指南，帮助开发者使用 VS Code 进行开发、运行、调试和部署其应用程序。

640?wx_fmt=png

作者 | Bruno Borges，微软首席工程师

译者 | 安翔

责编 | 屠敏

出品 | CSDN（ID：CSDNnews）

Visual Studio Code 已经成为多语言开发者首选的文本编辑器。Javascript、TypeScript、Go、Python 以及其他编程语言的大量开发者都习惯使用 VS Code 进行编码，VS Code 除了拥有良好的生态之外，它还具有强大而丰富的功能以及良好的用户体验，同时还能做到简洁快速和轻量级，这些因素使其成为一款无比强大的 IDE。

毫无疑问，如此强大的 VS Code 当然支持 Java，许多 Java 大牛和演讲者都选择它来进行现场演示。

接下来，我们将详解如何在 VS Code 中基于 Java 进行开发。如果你尚未下载 Visual Studio Code，请立即安装。本指南的其余部分要求你至少安装了 Java 8，当然 Java 11 也可以。你也可以完全跳过本指南，直接去看 Visual Studio Code 的 Java 文档。但是本文的一些干货可以帮助你充分利用 VS Code 进行 Java 开发。


640?wx_fmt=png

基本设置


一些扩展的存在使得 Java 能够得到 VS Code 最核心的支持。让我们深入研究一下这些扩展。

微软的 Java 扩展包

该扩展包包含了后面将会详细介绍的五个扩展，有了它，你无需对 VS Code 有太多了解即可使用它来进行 Java 开发。

红帽对 Java 的语言支持

想要获得 VS Code 对 Java 的支持，只需安装该扩展即可实现。其他的扩展能够起到锦上添花的作用，你可以根据项目具体情况酌情使用。

安装语言支持后，你便可以阅读和编辑 Java 源代码了。首先创建一个名为HelloWorld.java 的文件并在 VS Code 中打开（或者在 VS Code 中创建文件，然后将其保存到某个文件夹中也行）。  

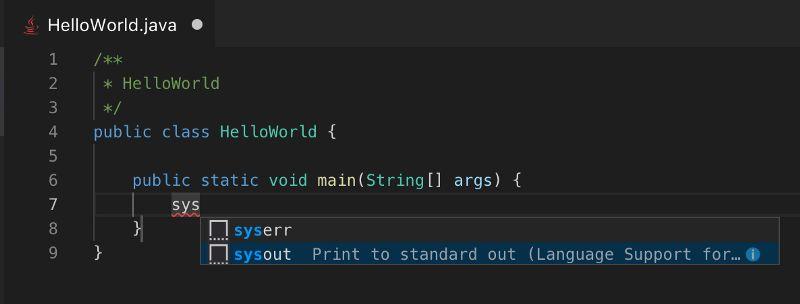
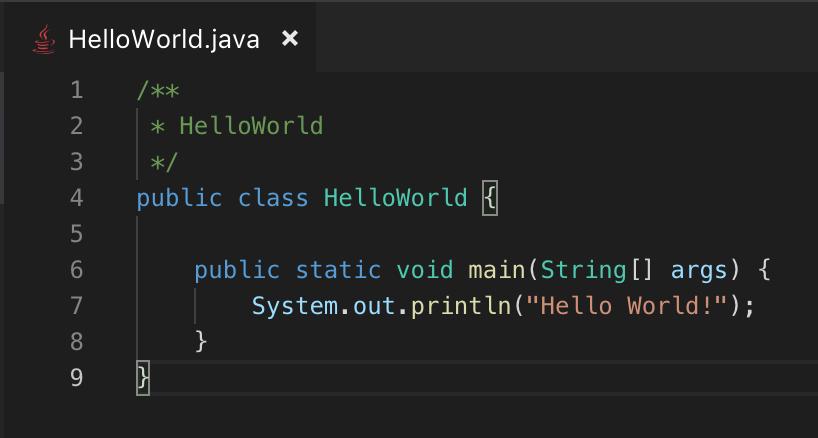
640?wx_fmt=png

640?wx_fmt=png

640?wx_fmt=png

640?wx_fmt=png

接下来，打开终端，以 Mac OS 为例，键入 ⌘+` - 然后输入 javac HelloWorld.java指令进行编译。

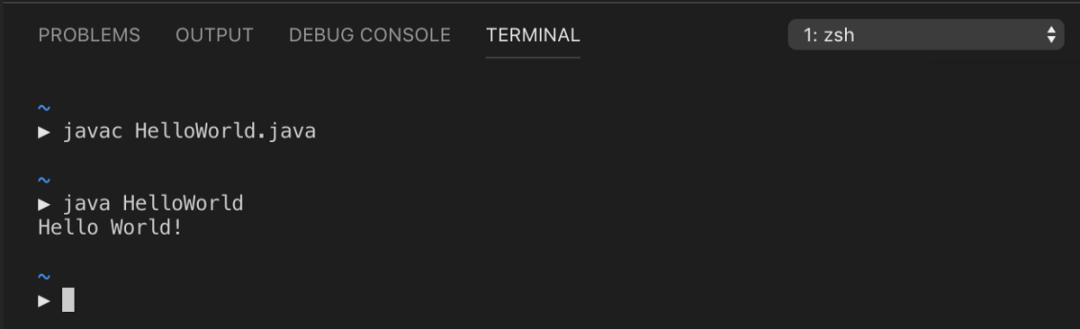
640?wx_fmt=png

这将生成一个名为 HelloWorld.class 的文件。执行 java HelloWorld 命令即可运行该程序。

Java 扩展的语言支持之所以能够支持 Java，主要借助于 Eclipse LSP。

其他特性

此扩展添加了许多其他功能，可以帮助开发者快速浏览、编写、重构和读取 Java源代码，以至于开发者可以放弃 IDE 转而选择轻量级的文本编辑器。

640?wx_fmt=png

有关重构和完整的功能列表，点击此处了解更多。

微软的 Java 调试器

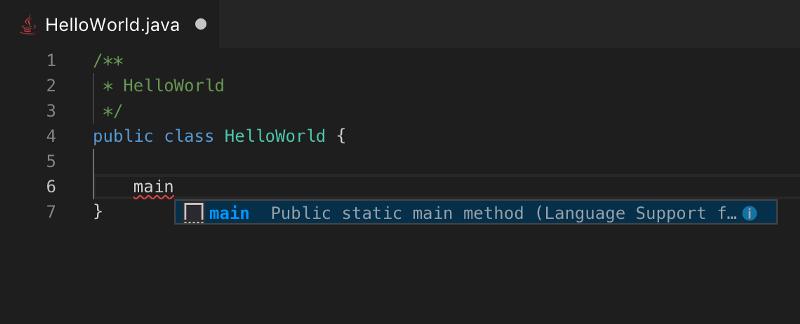
掌握了在 Visual Studio Code 中编写和阅读 Java 代码的基础知识之后，下一步学习程序的运行和调试。该扩展提供了这一点。它将使用你计算机上的默认JAVA_HOME 环境变量，当然，你也可以自定义。

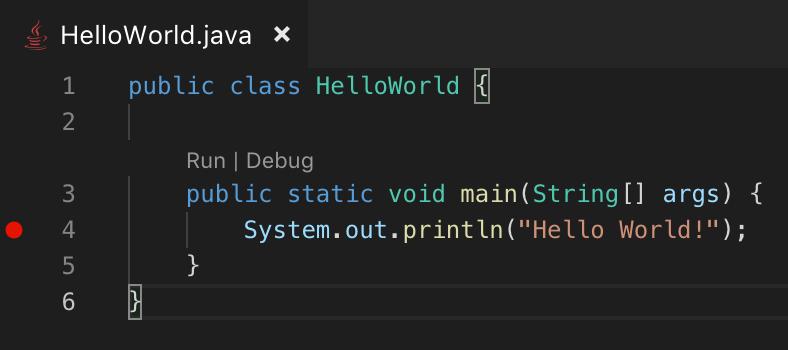
640?wx_fmt=png

它具备普通 Java IDE 的所有调试功能，开发者使用它可以更好地定制和控制事物的执行方式，掌握调试器连接到 JVM 的具体细节。此外，它还可以与远程 JVM 很好地配合工作。

安装此扩展之后，如上图所示，你会发现 main 方法上方有两个超链接，分别是 Run 和 Debug。点击“Run”，代码将被编译和执行。你还可以点击 Debug 并设置断点进行调试。 

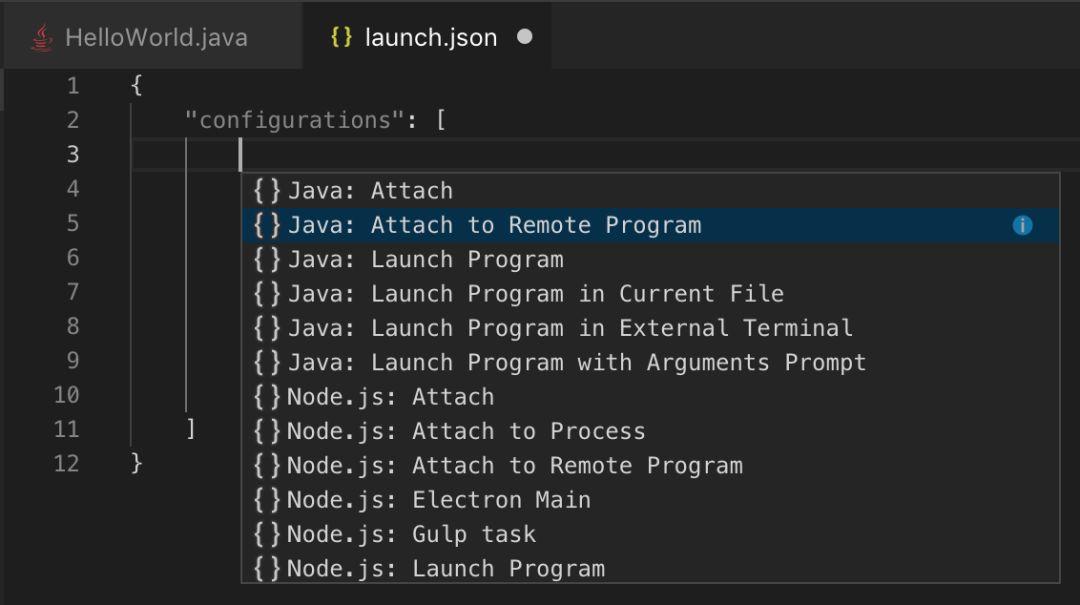
640?wx_fmt=png

想要进行远程调试，你得添加新的配置。转到 Debug 视图（在 Mac 上按下 Shift +⌘+ D）并按下齿轮 ⚙ 配置按钮。这将打开 launch.json 文件。点击屏幕上蓝色的  Add Configuration（添加配置） 按钮。这会弹出一个菜单，如上图所示。

此时，你可以自定义一个连接远程 JVM 的启动程序。只需提供主机名和端口号等信息即可。

与任何 IDE 的调试方法一样，你可以在程序执行期间跟踪变量和堆栈信息，也可以对变量内容进行更改。

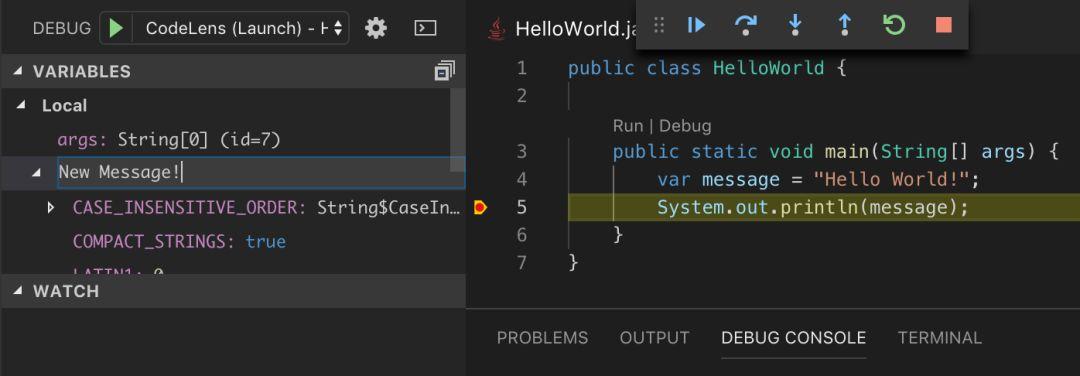
640?wx_fmt=png

自此，关于 Visual Studio Code 的基本设置已经完成，我们可以用其读取、编写、运行和调试 Java 代码。


640?wx_fmt=png

中级设置


只要你拥有 Java 编程的基础知识，那么你肯定会经常用到各种库、依赖项、类，等等。在 Visual Studio Code 中提升 Java 支持力度的最佳方法是添加以下扩展：

  1. Java 依赖查看器

  2. Maven for Java

接下来，我们一个一个详细介绍。

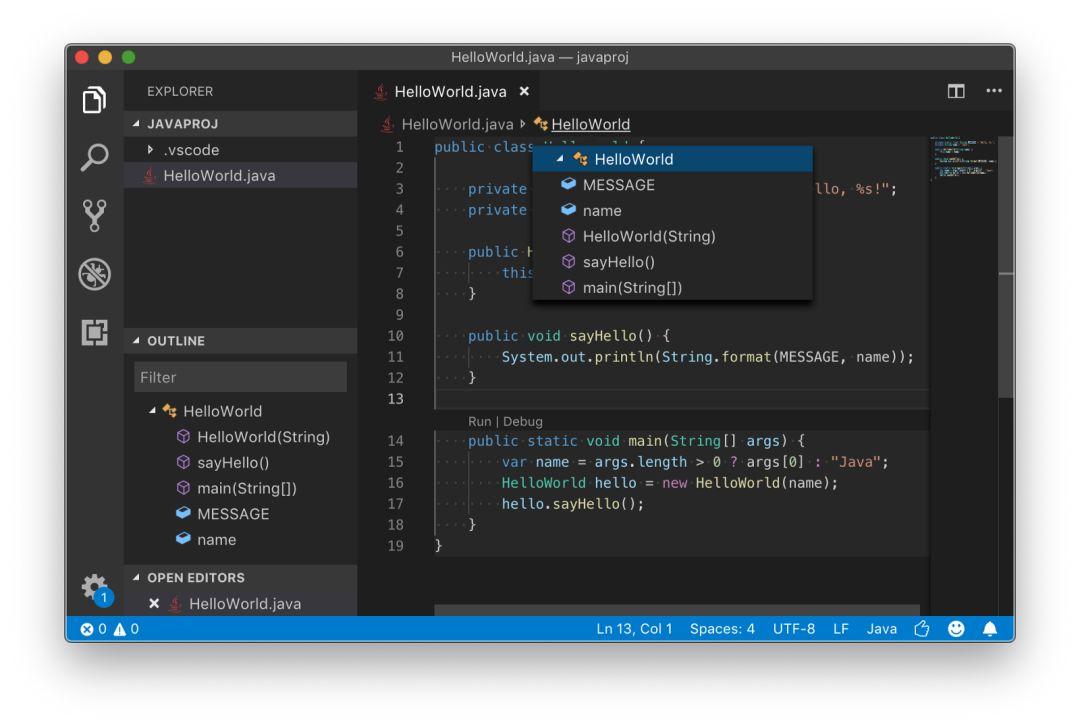
微软的 Java 依赖查看器

该扩展将为开发者提供两大核心功能。其中一个是“项目”的概念，开发者可以使用它来手动添加库（JAR）。第二个是它允许开发者可视化当前项目设置的类路径，即使它是 Maven 项目也可以。

打开命令行（Shift +⌘+ P）并键入 create java：

640?wx_fmt=png

你将看到项目创建的路径提示。项目所在文件夹的名称将与项目名相同。

创建项目后，VS Code 将在新窗口中打开这个新的文件夹。

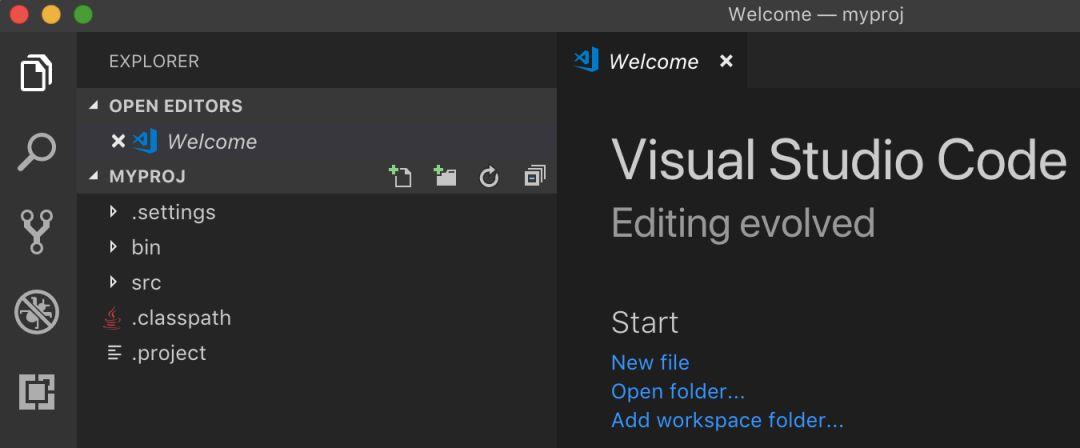
640?wx_fmt=png

如你所见，该项目具有 bin 和 src 文件夹的基本结构。在 src 中，你可以找到一个基本的 Java 类开始编写代码。如果你是一位经验丰富的 Java 开发人员，那么你将很快发现该扩展使用了与 Eclipse 类似的项目格式，它与 Eclipse LSP以及其他扩展一起使用效果将会更好。

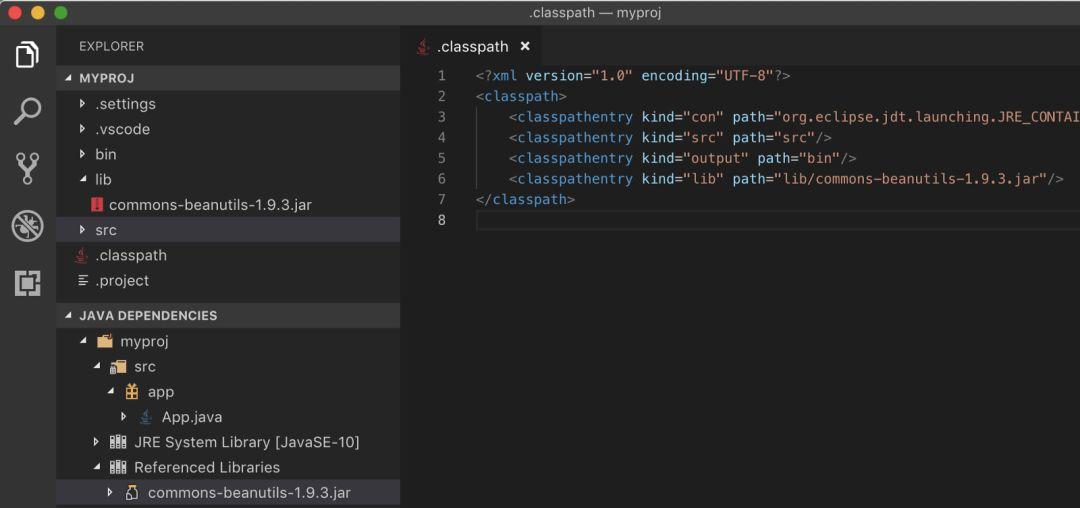
添加库和 JAR 包

你可以编辑 .classpath 文件来添加库。该扩展将自动在类路径中加载这些库，从而运行代码将会变得轻而易举。

640?wx_fmt=png

微软提供的 Maven for Java

Maven 是 Java 生态系统中使用最广泛的项目构建和依赖管理工具。因此，该扩展可以帮助你通过 Visual Studio Code 应对几乎任何类型的 Java 项目。

你可以通过 Maven 原型（骨架）生成和引导 Maven 项目，管理依赖项并触发Maven 目标，还可以通过一些智能代码来编辑 pom.xml 文件。

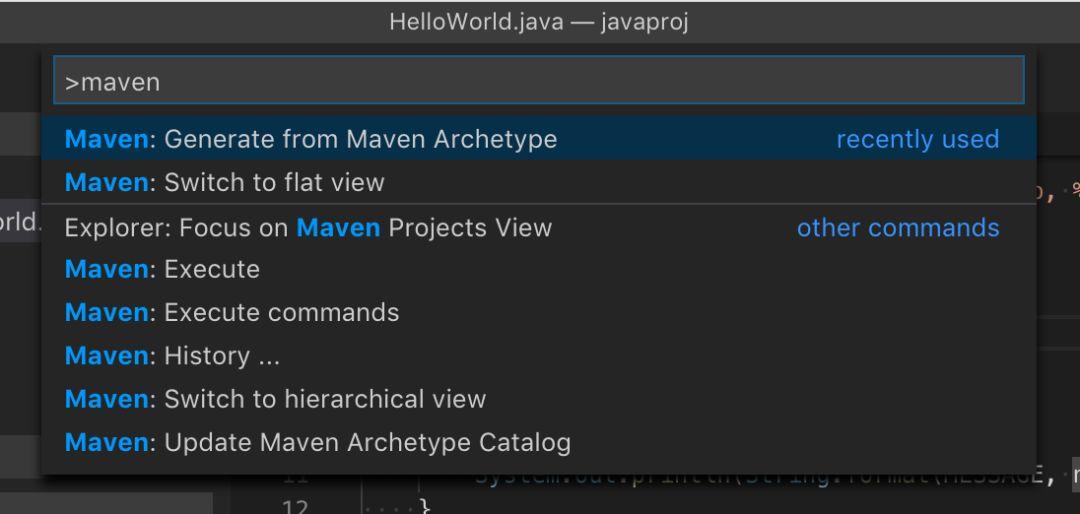
640?wx_fmt=png

进行如下操作：

  • 再次打开命令行，然后键入 Maven。

  • 选择  Generate from Maven Archetype。

  • 选择 maven-archetype-quickstart。

扩展程序将询问目标文件夹，项目文件夹将会自动生成到该目标文件夹中。之后会打开一个终端，你需要在该终端上输入 Maven 命令行的参数，这些都会自动引导，因此完全不必担心。

项目创建完成之后，在终端右侧调用 code <文件夹名称>。

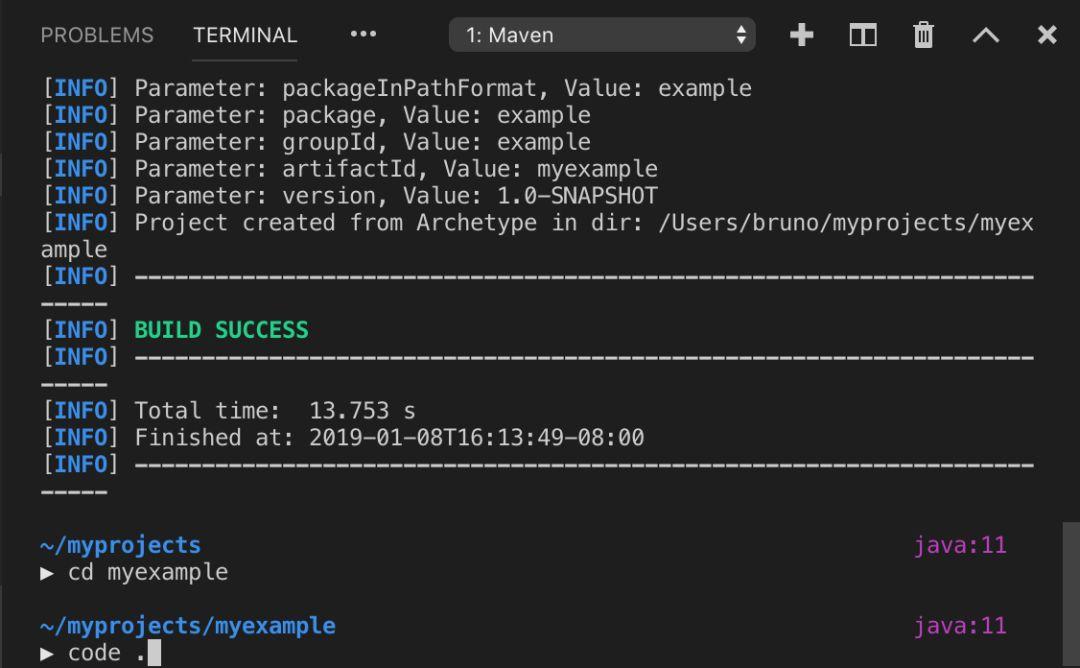
640?wx_fmt=png

此时，你的 Maven 项目应该已经在 VS Code 中打开了。有两种方式可以运行你的代码：

  1. 点击 main 方法旁边的 App 类中的名为 Run 的超链接。

  2. 当然，也可以使用 Maven。

如果使用 Java 扩展调试器（Run | Debug）触发器，扩展将使用 Maven 生成的类路径，以确保所有依赖项都正确添加到类路径中。

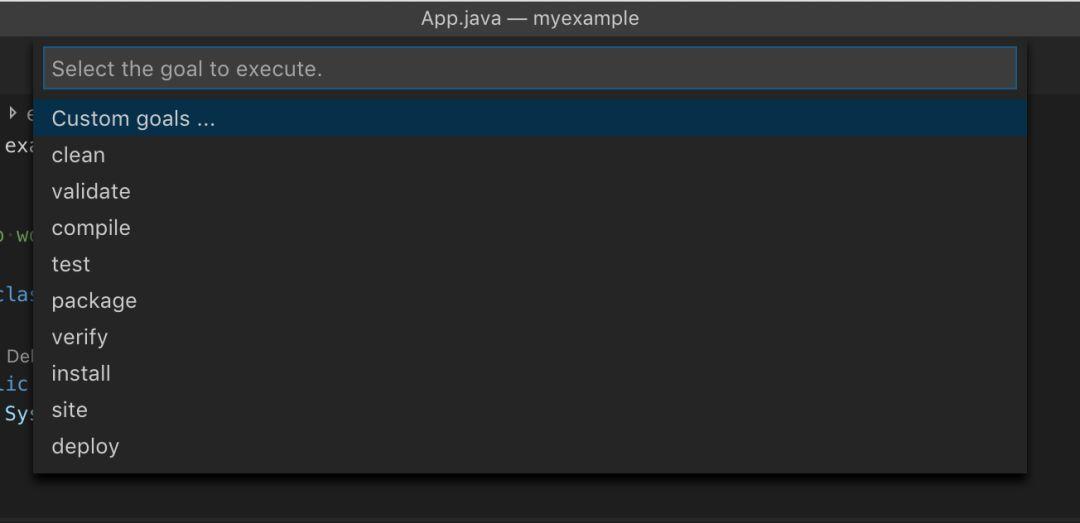
但是，要与 Maven 一起运行，你可以像往常一样使用终端，或者打开命令行并键入 Maven Execute Commands。 

640?wx_fmt=png

它会要求你选择一个项目。由于你只有一个项目，按下 Enter 键即可。接下来，你将看到所有默认核心 Maven 目标的列表。点击 package 以生成 JAR 文件。

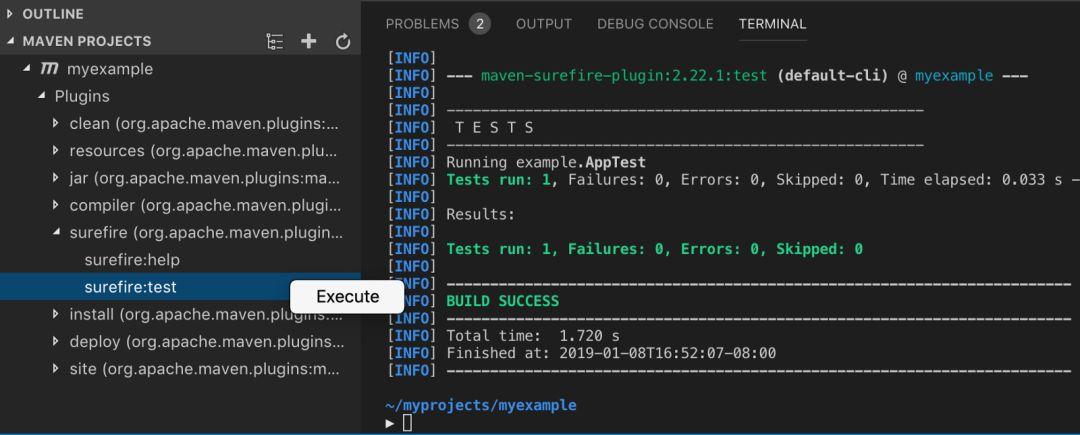
640?wx_fmt=png

如果要运行自定义目标，例如从 Maven 插件继承的目标，可以使用 Maven 视图：

640?wx_fmt=png

编辑 pom.xml 文件以添加依赖项，VS Code 将自动重新加载类路径，它将从新的依赖项中导入类和包。

微软的 Java Test Runner

该部分的内容能够帮助你更好地运行、调试和可视化单元测试结果。此扩展添加了可单独执行的单元测试（支持 JUnit 和 TestNG ）的超链接，你可以在 Visual Studio Code 中即刻查看报告，如下例所示。

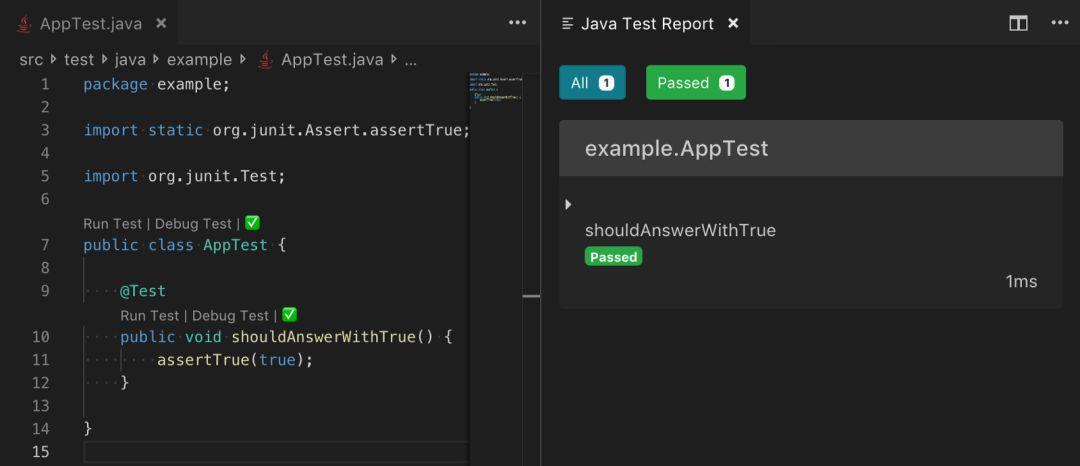
640?wx_fmt=png

此扩展还将启用 Test Explorer 视图，因此你可以专注于代码的单元测试并以更TDD 的风格编写软件。

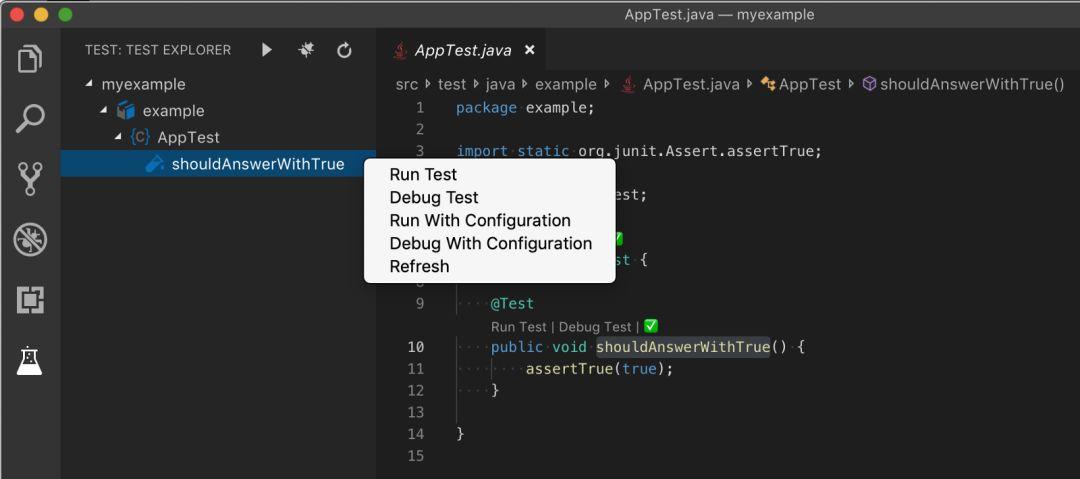
640?wx_fmt=png

此扩展目前仅适用于 Maven 项目，因此请确保你安装了 Maven for Java 扩展。


640?wx_fmt=png

高级设置


如果你现在对使用 VS Code for Java 已经得心应手了，那么现在是时候学习一些高级技能了。下面的扩展程序能够让你的日常工作如虎添翼。

GitLens

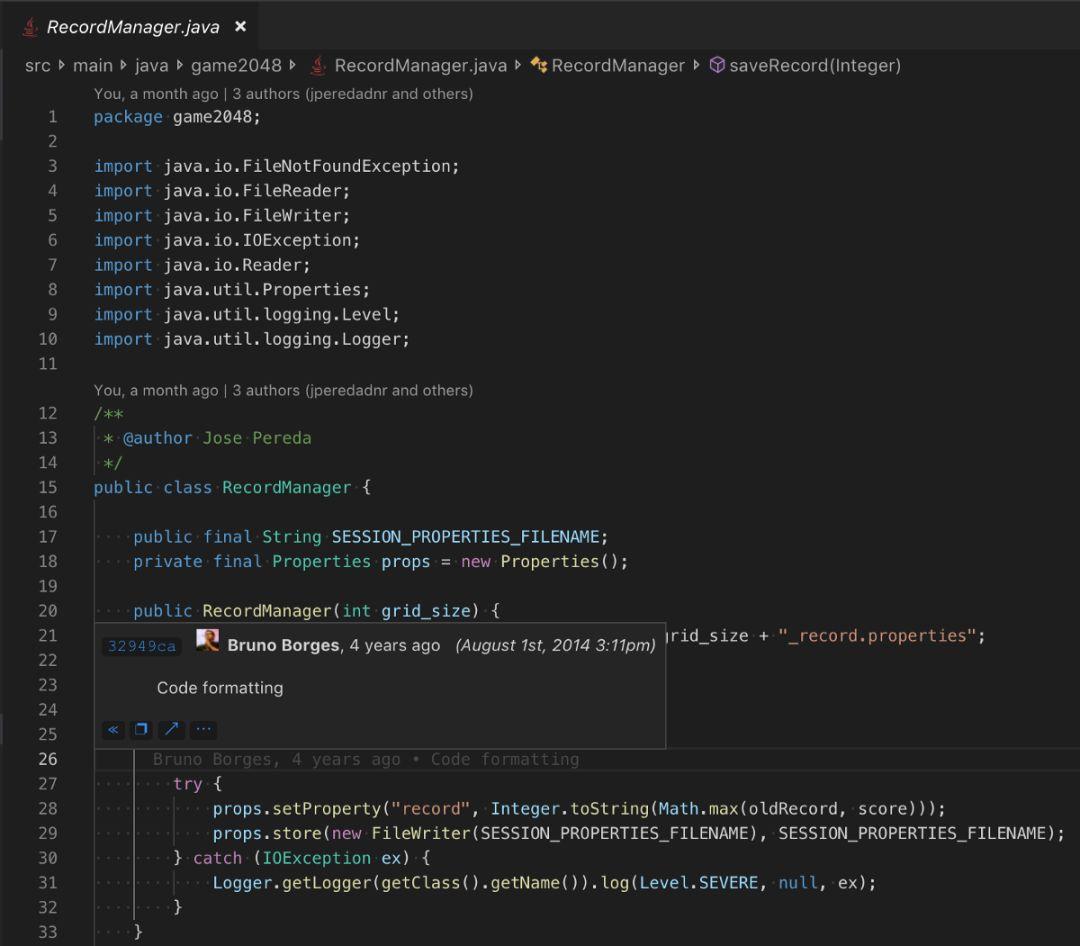
640?wx_fmt=png

希望你已经学会了使用 Git，无论是通过 GitHub 还是其他任何方式。此扩展程序可以帮助你了解源代码的修改者的历史记录，例如“何人何时添加了此方法”。

安装了 GitLens 之后，Java 类的样子将如上图所示。26行显示了修改者的历史信息。你也可以简单地将鼠标悬停在特定的行上，它将显示何人何时修改了该行代码。

REST 客户端

如果你是构建 REST API 的开发人员，那么这是 Visual Studio Code 环境中必须安装的扩展。有了它，你能够编辑包含 HTTP 调用的 .http 文件。编辑器将提供快速的代码片段和模板，它会在你点击后提供神奇的超链接，还会触发 HTTP 调用并在其旁边打开结果。如下图所示：

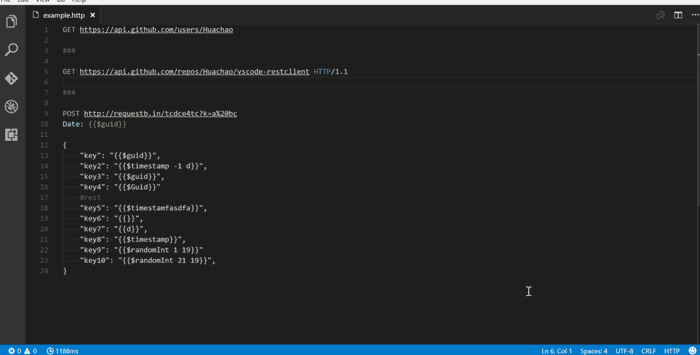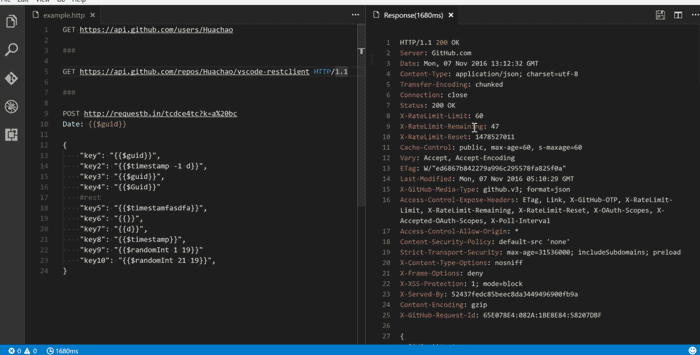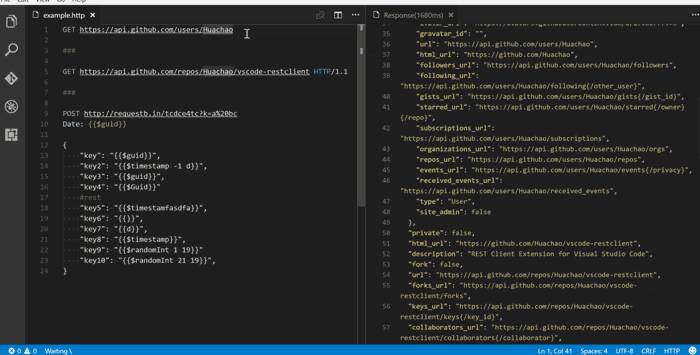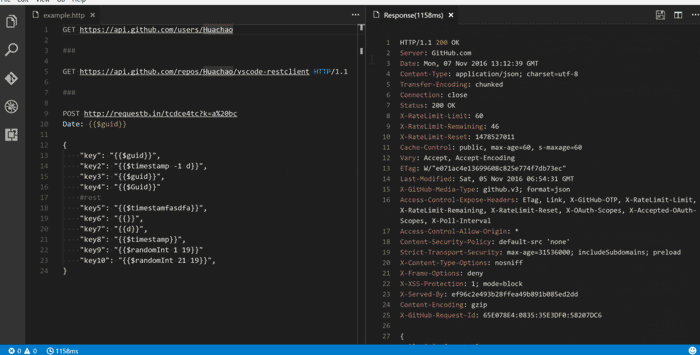
640?wx_fmt=gif

至此，我们拥有了一个完整的 Visual Studio Code 设置，可以进行任何类型的Java 开发。


640?wx_fmt=png

其他扩展程序：Spring Setup 和 Gradle


如果你是一个 Spring 开发人员，Pivotal 和微软提供的 Spring Setup 扩展将为你带来 Spring Boot 应用程序开发的良好体验。

最后，有一个名为 Gradle 的扩展可以帮助你编写 build.gradle 文件。

以下是其他一些值得了解的 Spring 工具：

  • Spring Boot Tools：https://marketplace.visualstudio.com/items?itemName=Pivotal.vscode-spring-boot&WT.mc_id=medium-blog-brborges

  • Spring Initializr Java Support：https://marketplace.visualstudio.com/items?itemName=vscjava.vscode-spring-initializr&WT.mc_id=medium-blog-brborges

  • Spring Boot Dashboard：https://marketplace.visualstudio.com/items?itemName=vscjava.vscode-spring-boot-dashboard&WT.mc_id=medium-blog-brborges

  • Gradle Language Support：https://marketplace.visualstudio.com/items?itemName=naco-siren.gradle-language&WT.mc_id=medium-blog-brborges

原文：https://dzone.com/articles/visual-studio-code-for-java-the-ultimate-guide-201

本文为 CSDN 翻译，如需转载，请注明来源出处。

 热 文 推 荐 

☞ 任正非：美国不会摧毁华为！

☞ 程序员跳槽面试刷题必备，微软工程师放大招！| 程序员硬核评测

☞ 可视化编程真的有那么糟糕？

☞ 滴滴“不差钱”？

☞ Java 工程师成神之路！

在使用 Go 两年之后，我又转回 PHP 了

微服务、Kubernetes和无服务器之后，即将发生的……

☞ 打打游戏就能在北京二环买套房？区块链大神说：你能靠VR刷怪升级还房贷！

帅气中国小哥出“大招”，程序员跳槽面试刷题必备

☞ 35岁程序员 节后第一天被辞退！

 
 
print_r('点个好看吧！');
var_dump('点个好看吧！');
NSLog(@"点个好看吧！");
System.out.println("点个好看吧！");
console.log("点个好看吧！");
print("点个好看吧！");
printf("点个好看吧！\n");
cout << "点个好看吧！" << endl;
Console.WriteLine("点个好看吧！");
fmt.Println("点个好看吧！");
Response.Write("点个好看吧！");
alert("点个好看吧！")
echo "点个好看吧！"
 
 
640?wx_fmt=gif点击“阅读原文”，打开 CSDN App 阅读更贴心！
 
 640?wx_fmt=png 
 喜欢就点击“好看”吧！ 


                

        

        
        

          

            
            

              

                CSDN
                

                  
                  微信公众号
                  
                

              

              成就一亿技术人
            

          

    

        

        
        
             
                

                    
        动态规划（Dynamic Programming, DP）是一种解决复杂问题的算法设计技术，它通过将大问题分解为小问题，并利用小问题的解决方案来构造大问题的解决方案，从而避免了重复计算。动态规划通常用于具有“最优子结构”和“重叠子问题”特征的问题。
 

动态规划的基本步骤
 

  1. 定义状态：明确问题的状态表示。即如何用状态表示当前的子问题。
  2. 状态转移方程：根据问题的结构，找到从一个状态转移到另一个状态的方式。
  3. 初始化：为基础情况设置初始值。
  4. 计算顺序：确定计算的顺序，从最小的子问题开始逐步计算到原问题。
  5. 答案提取：从动态规划表中提取最终答案。
 

动态规划的典型应用场景
 

  • 最短路径问题（如 Dijkstra、Floyd 算法）。
  • 背包问题（如 0/1 背包、完全背包）。
  • 字符串匹配问题（如最长公共子序列、编辑距离）。
  • 最优子结构问题（如矩阵链乘法问题、切割钢条问题）。
 

动态规划的分类
 

动态规划的算法通常可以分为以下两种类型：
 

  1. 自顶向下的递归式动态规划（Top-Down with Memoization）：
 

        使用递归进行问题的求解，并通过记忆化（Memoization）保存已计算的结果，避免重复计算。
 

  1. 自底向上的迭代式动态规划（Bottom-Up with Tabulation）：
 

        通过迭代从最小子问题开始，逐步解决更大的子问题，直到得到最终结果。
 

动态规划的三大特点
 

  1. 最优子结构：问题的最优解可以通过子问题的最优解来构造。例如，最长公共子序列问题的最优解可以通过子问题的解来构造。
  2. 重叠子问题：不同的子问题可能会多次出现，因此可以通过记忆化来存储已解决的子问题，避免重复计算。
  3. 状态转移：通过当前状态和已解决的子问题来推导出下一个状态。
 

动态规划的经典问题
 

1. 0/1 背包问题
 

问题描述：
 

  • 有一个背包，最多可以容纳重量为 W 的物品。
  • 有 n 个物品，每个物品的重量是 w[i]，价值是 v[i]。
  • 问：如何选择物品，使得背包的总价值最大，且总重量不超过 W？
 

动态规划解法：
 

  • 定义状态 dp[i][j]：表示前 i 个物品，背包容量为 j 时的最大价值。
  • 状态转移方程： 
  
    • 如果不选择第 i 个物品：dp[i][j] = dp[i-1][j]
    • 如果选择第 i 个物品：dp[i][j] = dp[i-1][j-w[i]] + v[i]
    • 最终的状态转移方程为：dp[i][j] = max(dp[i-1][j], dp[i-1][j-w[i]] + v[i])
 

  1. #include 
  2. #include 
  3. #include 
  4. using namespace std;
  5.  
  6. int knapsack(int W, vector<int>& w, vector<int>& v, int n) {
  7.     // dp[i][j]表示前i个物品，容量为j时的最大价值
  8.     vectorint>> dp(n + 1, vector<int>(W + 1, 0));
  9.  
  10.     for (int i = 1; i <= n; i++) {
  11.         for (int j = 1; j <= W; j++) {
  12.             if (w[i - 1] <= j) {
  13.                 // 当前物品不放入或放入两种选择的最大值
  14.                 dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i - 1]] + v[i - 1]);
  15.             } else {
  16.                 dp[i][j] = dp[i - 1][j]; // 当前物品不能放入
  17.             }
  18.         }
  19.     }
  20.     return dp[n][W]; // 返回最大价值
  21. }
  22.  
  23. int main() {
  24.     int W = 10; // 背包容量
  25.     vector<int> w = {2, 3, 4, 5}; // 物品重量
  26.     vector<int> v = {3, 4, 5, 6}; // 物品价值
  27.     int n = w.size();
  28.  
  29.     cout << "Max value in knapsack: " << knapsack(W, w, v, n) << endl;
  30.     return 0;
  31. }
 

输出：
 

Max value in knapsack: 7
 

2. 最长公共子序列问题
 

问题描述：
 

  • 给定两个字符串 s1 和 s2，求它们的最长公共子序列（LCS）。
 

动态规划解法：
 

  • 定义状态 dp[i][j]：表示 s1[0...i-1] 和 s2[0...j-1] 的最长公共子序列长度。
  • 状态转移方程： 
  
    • 如果 s1[i-1] == s2[j-1]，那么 dp[i][j] = dp[i-1][j-1] + 1
    • 否则，dp[i][j] = max(dp[i-1][j], dp[i][j-1])
 

  1. #include 
  2. #include 
  3. #include 
  4. using namespace std;
  5.  
  6. int longestCommonSubsequence(string s1, string s2) {
  7.     int m = s1.size(), n = s2.size();
  8.     vectorint>> dp(m + 1, vector<int>(n + 1, 0));
  9.  
  10.     for (int i = 1; i <= m; i++) {
  11.         for (int j = 1; j <= n; j++) {
  12.             if (s1[i - 1] == s2[j - 1]) {
  13.                 dp[i][j] = dp[i - 1][j - 1] + 1;
  14.             } else {
  15.                 dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
  16.             }
  17.         }
  18.     }
  19.     return dp[m][n]; // 返回最长公共子序列长度
  20. }
  21.  
  22. int main() {
  23.     string s1 = "abcde";
  24.     string s2 = "ace";
  25.  
  26.     cout << "Length of Longest Common Subsequence: " << longestCommonSubsequence(s1, s2) << endl;
  27.     return 0;
  28. }
 

输出：
 

Length of Longest Common Subsequence: 3
 

3. 斐波那契数列
 

斐波那契数列是经典的动态规划问题。其定义是：
 

  • F(0) = 0
  • F(1) = 1
  • F(n) = F(n-1) + F(n-2)
 

动态规划解法通过迭代避免了递归中的重复计算。
 

  1. #include 
  2. using namespace std;
  3.  
  4. int fib(int n) {
  5.     if (n <= 1) return n;
  6.     
  7.     int prev2 = 0, prev1 = 1;
  8.     for (int i = 2; i <= n; i++) {
  9.         int curr = prev1 + prev2;
  10.         prev2 = prev1;
  11.         prev1 = curr;
  12.     }
  13.     return prev1;
  14. }
  15.  
  16. int main() {
  17.     int n = 10;
  18.     cout << "Fibonacci of " << n << " is " << fib(n) << endl;
  19.     return 0;
  20. }
 

输出：
 

Fibonacci of 10 is 55
 

总结
 

        动态规划是一种通过将问题分解成小问题并利用已解决的小问题来避免重复计算的技术。其核心思想是使用状态表示问题的不同阶段，并通过状态转移方程来递推求解。在实际应用中，动态规划非常适用于具有“最优子结构”和“重叠子问题”特征的问题，常见的问题有背包问题、最长公共子序列、矩阵链乘法等。

                

        

    

                

                

                    注：本文转载自blog.csdn.net的CSDN资讯的文章"https://blog.csdn.net/csdnnews/article/details/87746061"。版权归原作者所有，此博客不拥有其著作权，亦不承担相应法律责任。如有侵权，请联系我们删除。
                

                

                    

                        

                            

                                
                                
                                
                                
                                    
                                
                                
                                
                                
                                
                                
                                
                                
                                
                                
                                

                                    复制链接
                                    
                                

                                

                                    
                                    

                                        

                                            

                                        

                                    

                                

                            

                        

                    

                


                

                    





                        
                    

                

                

                
            



            

            

                
相关推荐

                

                    

                    

                

            

            

                

                    

                        

							
								发表评论
                        

                        
                    

                    

                        

                            

								
                            

                            

                                

                                    

                                        
                                    

                                    

                                        
                                    

                                

                            

                            

                                
                            

                        

                        
评论记录：

                        
                        
                        
                        
                        
                        
未查询到任何数据！