
概述:要求身高1.76以上(因为本人身高1.70),精通C++编程(起码要比我水平高), 24岁以上因为本人>23岁&&本人<24岁),身体强壮(这样会有安全感),在长沙工作(因为本人不打算到别处去),本次征友的主要原因:受不了老妈的热心,次要原因:想找一个志同道和的人。
本人简介:在长沙从事计算机行业两年,虽然水平不高,但有志于成为一个专家,坚持认为只有从coder做起才会真正成为高手,崇拜c++高手,业余时间喜欢音乐和看电影。
UseCase1:
基本路径:
1:你是一个真诚的人,不是玩玩而已
2:留给我你的基本条件及基本联系方式
3:我认为合适会联络你
4:尝试成为朋友
5:成为恋人
6:结婚
异常路径:
1:第3步我认为不合适
2:不会联系你,十分抱歉,希望你会有更好的缘分!
以下是网友回复
回复1:
项目完成后强烈要求其公布开发文档、测试文档和维护文档。
回复2:
不合适你直接把人家GOTO到:不会联系你,十分抱歉,希望你会有更好的缘分!
回复3:
寻男友过程一定要遵照CMM5规范来执行,争取这个项目要成为CMM5模范工程!
现在成立CMM评审小组,愿意参加的报名……
回复4:
你的文档不能通过ISO2002-SW-CMM1,项目不能通过,去问问技术总监吧!
回复5:
CMM小组一至决定需求不通过,完全不能对需求方所提供资料进行分析(比如说:需求方条件,照片等),所以这个评审失败。
回复6:
强烈要求公布开发文档、测试文档和维护文档、如果可能也公开源代码。
回复7:
//本程序在Microsoft VisualC++ .NET 55601-652-0000007-18074下编译通过
//版本1.0 共享软件(C)版权所有 2003
BOOL IfYourWantToFindSomeOne(){
do{
if(Has_Photos()){
//有照片
if(身高==My.男友.身高.180CM&& 相貌==My.男友.相貌 && OtherConditions()){
return TRUE;
}
else {
return FALSE;
}
}
else{
if(That_Man_Is_Good_Man()){ //好人还是坏人都很难说
return TRUE;
}
else{
Your_Meet_A_Bad_Man();//坏人多多,还是在身边找吧
return FALSE;
}
}
}
while(_404_No_Found_Boy_Friend() &&My.精力– && My.信心–)
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
回复8:
这个需求太简单了,说明你没有认真做需求分析,估计你的需求在你的“设计阶段”还会变更。
回复9:
TO 7:
程序错误:at line 18 of FindFriend.cpp:my.精力 no initlizeted
程序错误:at line 18 of FindFriend.cpp:my.信心 to initlizeted
呵呵可能是个warning
不过很危险哟搞不好会系统崩溃哟
回复10:
流程过于简单,异常分支考虑不严密,另外需求分析,对立项的目的和项目风险估算不够。不能算一份合格的需求说明。


注意力机制(Attention Mechanism) 是深度学习中一种模拟人类注意力分配的技术。其核心思想是:在处理输入数据时,模型能够动态地关注对当前任务更重要的部分,而忽略不相关的信息。例如,翻译句子时,模型在生成某个词时会更关注原句中对应的关键部分。
注意力机制通过动态聚焦关键信息、解决 Seq2Seq 长距离依赖、支持并行计算等特性,成为LLM的核心组件,使其能够理解复杂语言结构并生成人类水平的文本。
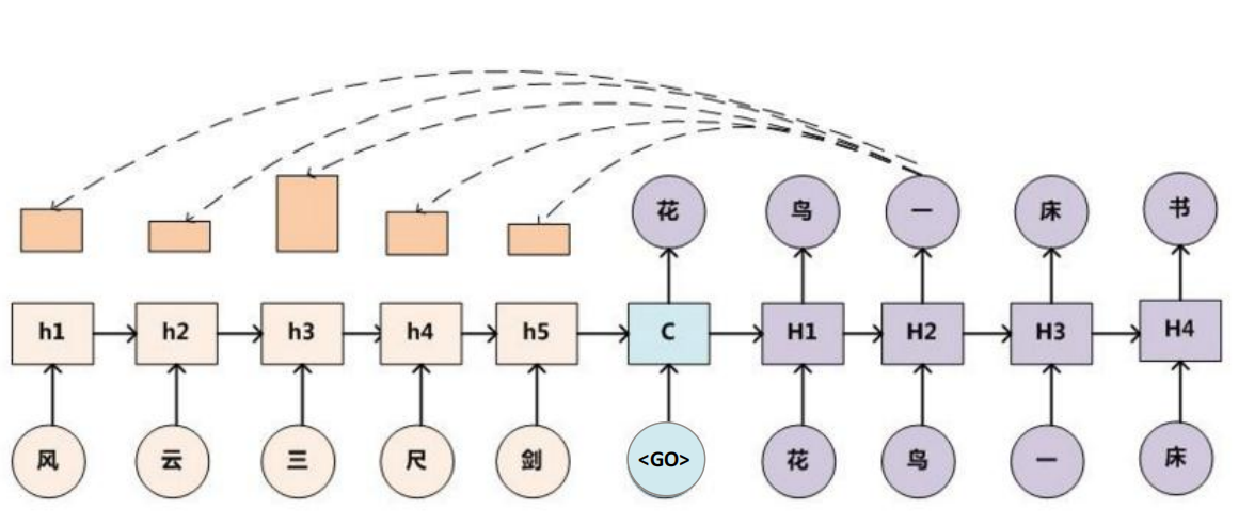
Seq2Seq Attention
MHA(Multi-Head Attention)
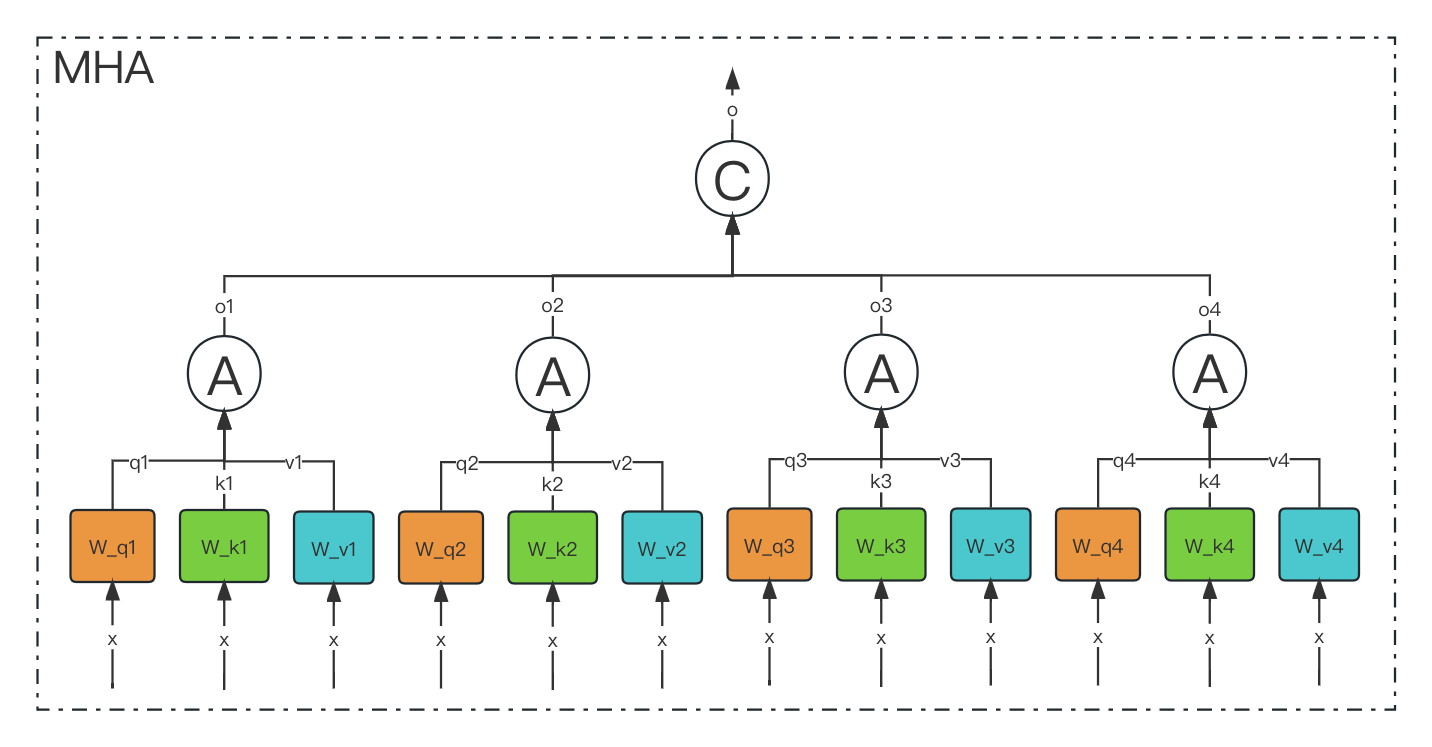
多头注意力(Multi-Head Attention,MHA) 是 Transformer 模型的核心组件,它通过并行化多组独立的注意力机制,显著提升了模型捕捉多样化语义关系的能力。以下是深入解析:
1. 核心思想:分而治之
- 类比:假设你让多个“专家”从不同角度分析同一段文本,每个专家关注不同的特征(如语法、语义、上下文关系等),最后综合所有专家的意见得出结论。
- 本质:将输入信息投影到多个子空间(subspace),在每个子空间独立计算注意力,最后合并结果。这比单一注意力机制能捕捉更丰富的特征。
2. 具体实现步骤
以输入序列维度 (batch_size, seq_len, d_model) 为例(例如 d_model=512):
-
线性投影: 将输入的 Query(Q)、Key(K)、Value(V)通过
h 个不同的线性层(权重矩阵),分割为h 个“头”(Head),每个头的维度为d_k = d_model / h(例如h=8 时,d_k=64):python代码解读复制代码Q_heads = [Q @ W_Qi for i in range(h)] # h 个 (batch_size, seq_len, d_k) K_heads = [K @ W_Ki for i in range(h)] V_heads = [V @ W_Vi for i in range(h)] -
独立计算注意力: 每个头分别进行缩放点积注意力(Scaled Dot-Product Attention):
python代码解读复制代码head_i = softmax(Q_i @ K_i.T / sqrt(d_k)) @ V_i # (batch_size, seq_len, d_k) -
拼接与融合: 将
h 个头的输出拼接(concat),再通过线性层融合:python代码解读复制代码combined = concat(head_1, head_2, ..., head_h) # (batch_size, seq_len, d_model) output = combined @ W_O # (batch_size, seq_len, d_model)
3. 为什么需要多头?
① 捕捉多样化的依赖关系
-
示例:在句子 “He picked up the book and put it on the shelf .” 中:
- 一个头可能关注 语义关联(“book”和“shelf”的类别关系);
- 另一个头关注 位置信息(“put”需要关联到“book”和“shelf”);
- 其他头可能关注 语法结构(动词“picked”的主语是“He”)。
② 增强模型鲁棒性
- 不同头可能学习到互补的注意力模式。即使某个头的权重出现偏差,其他头仍能提供有效信息(类似集成学习)。
③ 并行化计算效率
- 多个头可并行计算(GPU友好),实际计算速度与单头注意力接近。
4. 实际案例解析
案例 1:指代消解
text代码解读复制代码句子:"The lawyer questioned the witness because **she** was nervous."
- 头 1:关注“she”与“lawyer”的性别一致性;
- 头 2:关注“questioned”与“witness”的语义关联;
- 头 3:捕捉“because”引导的因果逻辑。
案例 2:多语言翻译
在翻译中文成语“胸有成竹”时:
- 头 1:捕捉字面意义(“胸”、“竹”);
- 头 2:关联隐含的英文习语“have a well-thought-out plan”;
- 头 3:调整语序以符合英文语法。
5. 关键超参数:头数(h)
-
典型值:Transformer 论文中
h=8,d_model=512(每个头d_k=64)。 -
平衡原则:
- 头数过多:每个头的维度
d_k 过小,可能丢失信息(如h=16 时d_k=32); - 头数过少:模型无法捕捉足够的多样性。
- 头数过多:每个头的维度
-
实验结论:
h=8 在大多数任务中表现最佳,但可根据数据复杂度调整。
6. MHA vs. 单头注意力
| 对比维度 | 多头注意力(MHA) | 单头注意力 |
|---|---|---|
| 特征多样性 | 多个子空间捕捉不同类型的关系 | 单一注意力模式 |
| 鲁棒性 | 对噪声或局部偏差更鲁棒 | 容易受单一注意力权重影响 |
| 计算效率 | 并行计算,速度与单头接近 | 相同计算量 |
| 模型容量 | 参数更多,表达能力更强 | 参数较少,可能欠拟合 |
7. MHA 的变体与优化
- 稀疏注意力(Sparse Attention):限制每个词只关注局部区域(如 Longformer),降低计算复杂度。
- 跨头参数共享:部分共享头的权重,减少参数量(如 ALBERT 模型)。
- 动态头数调整:根据输入内容自适应选择激活的头数(研究前沿)。
8 . KV Cache
在token by token递归生成时,新预测出来的第个 token,并不会影响到已经算好的,因此这部分结果我们可以缓存下来供后续生成调用,避免不必要的重复计算,这就是所谓的KV Cache。后面的MQA、GQA、MLA,都是围绕“如何减少KV Cache同时尽可能地保证效果”这个主题发展而来的产物。
总结
多头注意力通过分治策略,让模型从多角度理解上下文,是 Transformer 超越传统模型(如 RNN)的关键设计。它如同一个“多面手团队”,每个成员负责不同维度的分析,最终协同输出更全面、准确的结果。
问题
为什么降低KV Cache的大小如此重要?
LLM的模型需要在GPU上进行推理,且单张GPU的显存是有限的,其中一部分被用来存放模型参数以及在网络前向过程中激活函数计算值,这部分的大小取决于模型体量,GPU加载模型后这部分大小固定为常数不会发生改变,还有一部分就是 KV Cache,这部分取决于文本的长度,其动态的变化也就导致了当遇到长文本时可能会超出单卡的显存容量。
在GPU上部署模型的原则是:能一张卡部署的,就不要跨多张卡;能一台机部署的,就不要跨多台机。这是因为“卡内通信带宽 > 卡间通信带宽 > 机间通信带宽”,由于“木桶效应”,模型部署时跨的设备越多,受设备间通信带宽的的“拖累”就越大,事实上即便是单卡H100内SRAM与HBM的带宽已经达到了3TB/s,但对于Short Context来说这个速度依然还是推理的瓶颈,更不用说更慢的卡间、机间通信了。
减少KV Cache的目的就是要实现在更少的设备上推理更长的Context,或者在相同的Context长度下让推理的batch size更大,从而实现更快的推理速度或者更大的吞吐总量。
MQA(Multi-Query Attention)
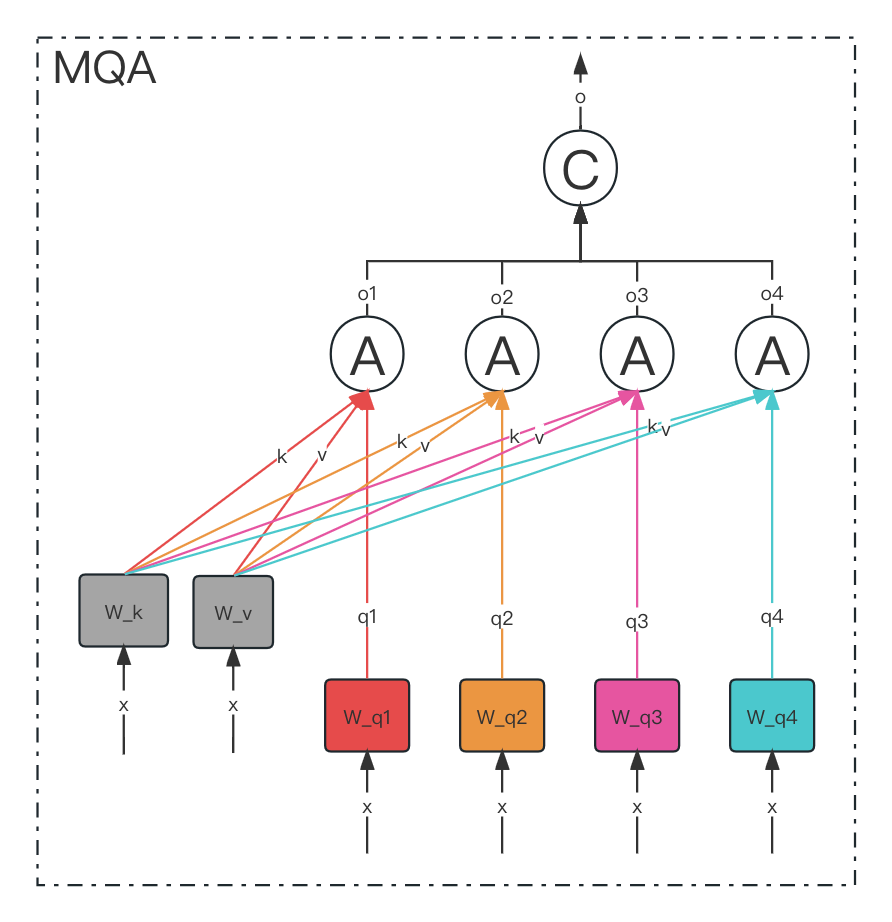
多查询注意力(Multi-Query Attention,MQA) 是一种优化后的注意力机制,通过共享键(Key)和值(Value)的投影矩阵,显著减少计算和内存开销,同时保持模型性能。以下是详细解析:
1. 核心思想:共享键值,保留多样查询
- 类比:想象一个团队讨论问题,多个成员(查询头)提出不同角度的问题(Q),但大家共享同一份参考资料(K和V)。这减少了重复准备材料的成本,但保留了多样化的提问视角。
- 本质:多个查询头(Multi-Query)共享同一组键和值的投影参数,仅保留独立的查询(Q)投影,从而降低计算复杂度。
2. 具体实现步骤
以输入序列维度 (batch_size, seq_len, d_model) 为例(如 d_model=512):
-
线性投影:
- 查询(Q) :仍被投影为
h 个独立的头(每个头维度d_k),如h=8,d_k=64。 - 键(K)和值(V) :仅投影为 1组(共享)的键和值,维度保持
d_k。
python代码解读复制代码# 独立投影查询(h个头) Q_heads = [Q @ W_Q1, Q @ W_Q2, ..., Q @ W_Qh] # h个(batch_size, seq_len, d_k) # 共享投影键和值(单头) K_shared = K @ W_K # (batch_size, seq_len, d_k) V_shared = V @ W_V # (batch_size, seq_len, d_k) - 查询(Q) :仍被投影为
-
独立计算注意力: 每个查询头与共享的键、值进行注意力计算:
python代码解读复制代码head_i = softmax(Q_i @ K_shared.T / sqrt(d_k)) @ V_shared # (batch_size, seq_len, d_k) -
拼接与融合: 与多头注意力(MHA)相同,拼接所有头并通过线性层融合:
python代码解读复制代码combined = concat(head_1, head_2, ..., head_h) # (batch_size, seq_len, d_model) output = combined @ W_O # (batch_size, seq_len, d_model)
3. 为什么需要MQA?
① 降低计算和内存开销
- 计算量对比:
MHA 的键值投影计算量为
2 * h * d_model * d_k,而 MQA 仅为2 * d_model * d_k(减少为1/h)。 - 显存占用:
键值缓存(KV Cache)的显存需求降低为 MHA 的
1/h,这对长序列生成任务(如对话系统)至关重要。
② 推理加速
- 示例:在自回归生成(如GPT)中,每次生成新词时需重复计算键值。MQA 通过共享键值,使推理速度提升 20-40% (实验数据)。
③ 平衡性能与效率
- 性能损失可控:MQA 在多数任务(如文本生成、翻译)中性能接近 MHA,尤其在模型规模较大时(如百亿参数以上)。
4. 实际案例解析
案例 1:大模型推理加速
-
场景:使用 GPT-4 生成长文本(如1000字文章)。
-
MQA 作用:
- 键值缓存显存减少为原来的
1/8(若h=8),允许批量处理更多并发请求。 - 单次生成延迟降低,用户体验更流畅。
- 键值缓存显存减少为原来的
案例 2:边缘设备部署
-
场景:在手机端运行轻量级语言模型(如问答助手)。
-
MQA 作用:
- 减少键值投影参数,模型体积缩小。
- 降低计算功耗,延长设备续航。
5. 关键设计选择
- 头数(h) :通常与 MHA 保持一致(如
h=8),但共享键值后,头数对计算影响大幅降低。 - 投影维度(d_k) :可适当增加共享键值的维度,补偿信息损失(如从64增至128)。
6. MQA vs. MHA
| 对比维度 | MQA(多查询注意力) | MHA(多头注意力) |
|---|---|---|
| 键值投影 | 1组共享 | h组独立 |
| 计算开销 | 最低(键值计算量降为 1/h) | 最高 |
| 显存占用 | 最低 | 最高 |
| 模型性能 | 接近MHA(小损) | 最优 |
| 适用场景 | 高吞吐量推理、资源受限环境 | 训练阶段或对精度要求极高的任务 |
7. MQA 的变体与优化
- 动态键值共享:根据输入内容动态选择是否共享键值(如重要词保留独立键值)。
- 混合注意力:部分层使用 MQA,部分层使用 MHA(如底层用MQA加速,顶层用MHA保精度)。
- 量化压缩:对共享的键值矩阵进行低精度量化,进一步减少显存占用。
总结
多查询注意力(MQA)通过共享键值投影,在几乎不损失性能的前提下,显著提升推理速度和降低资源消耗。它是大模型落地应用(如实时对话、边缘计算)的关键优化技术,完美诠释了 “少即是多” 的工程哲学——用更少的计算资源,实现更高效的智能。
GQA(Group-Query Attention)
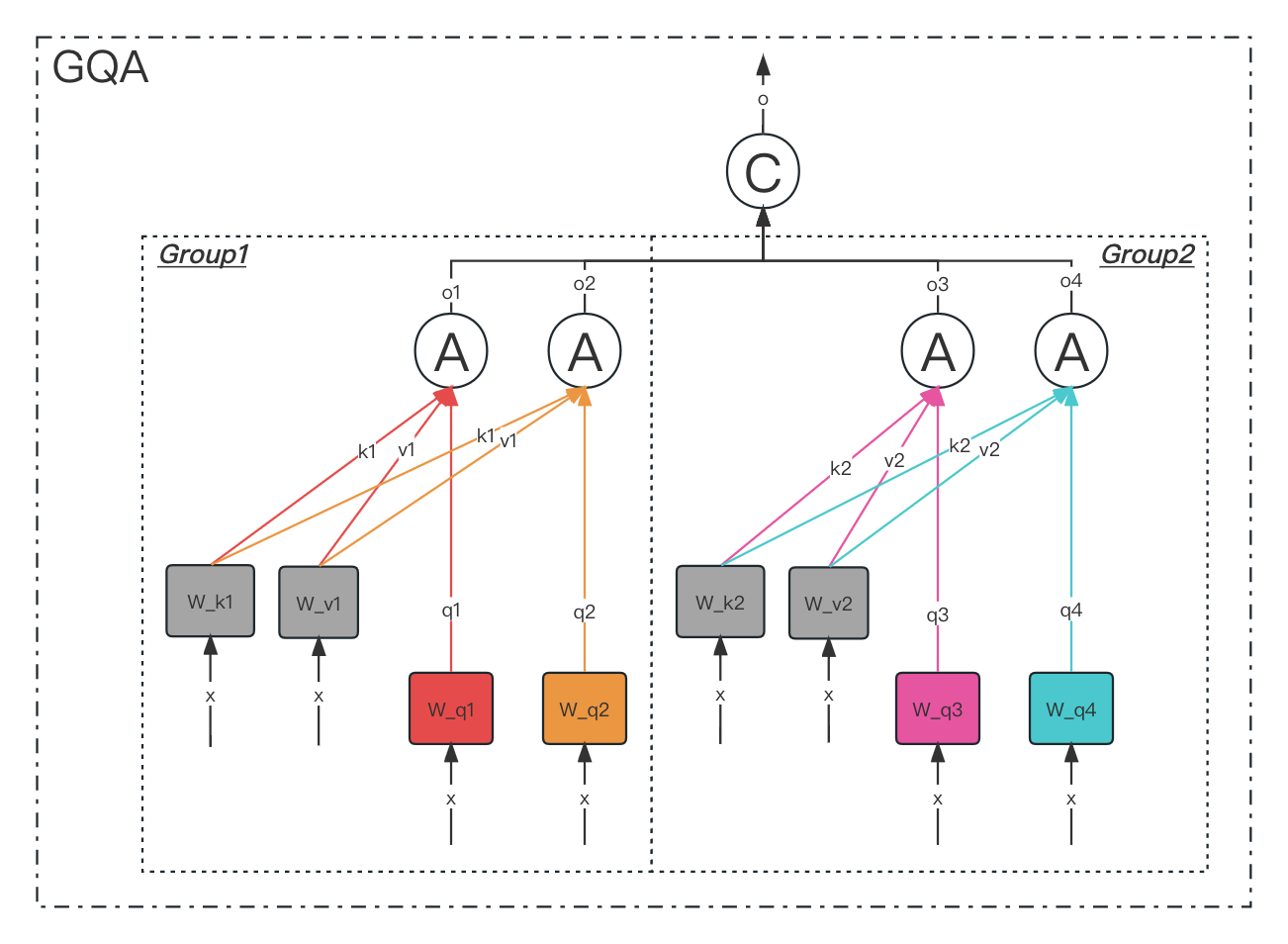
分组查询注意力(Group-Query Attention,GQA) 是介于多头注意力(MHA)和多查询注意力(MQA)之间的折中方案,通过将查询头(Query Heads)分组并共享键值(Key/Value)投影,平衡计算效率与模型性能。
1. 核心思想:分组共享键值
-
类比:将团队分成若干小组,组内成员共享参考资料(K/V),但不同组保留独立视角(Q)。例如,将8人团队分为2组,每组4人共享同一份资料,但各组提问角度不同。
-
本质:将查询头分为
g 组,每组内的所有查询头共享同一组键和值投影,组间保持独立。- 示例:若总头数
h=8,分组数g=2,则每组包含h/g=4 个查询头,共享1组键值投影。
- 示例:若总头数
2. 具体实现步骤
以输入序列维度 (batch_size, seq_len, d_model) 为例(如 d_model=512,h=8,g=2):
-
线性投影:
- 查询(Q) :投影为
h=8 个独立头,每个头维度d_k=64。 - 键(K)和值(V) :投影为
g=2 组(每组共享),每组维度d_k=64。
python代码解读复制代码# 独立投影查询(h=8个头) Q_heads = [Q @ W_Q1, Q @ W_Q2, ..., Q @ W_Q8] # 8个(batch_size, seq_len, d_k) # 分组投影键和值(g=2组) K_groups = [K @ W_K1, K @ W_K2] # 2组(batch_size, seq_len, d_k) V_groups = [V @ W_V1, V @ W_V2] # 2组(batch_size, seq_len, d_k) - 查询(Q) :投影为
-
组内注意力计算: 每组内的4个查询头共享同一组键值:
python代码解读复制代码# 组1:前4个查询头共享 K_groups[0] 和 V_groups[0] group1_heads = [softmax(Q_i @ K_groups[0].T / sqrt(d_k)) @ V_groups[0] for Q_i in Q_heads[0:4]] # 组2:后4个查询头共享 K_groups[1] 和 V_groups[1] group2_heads = [softmax(Q_i @ K_groups[1].T / sqrt(d_k)) @ V_groups[1] for Q_i in Q_heads[4:8]] -
拼接与融合: 合并所有头并通过线性层输出:
python代码解读复制代码combined = concat(group1_heads + group2_heads) # (batch_size, seq_len, d_model) output = combined @ W_O # (batch_size, seq_len, d_model)
3. 为什么需要GQA?
① 平衡效率与性能
- 计算开销:键值投影量从 MHA 的
2*h*d_model*d_k 降为2*g*d_model*d_k(当g=2 时减少为1/4)。 - 性能保留:组内共享键值,但组间保持独立,比 MQA 保留更多多样性(实验显示性能损失小于1%)。
② 灵活适配场景
- 通过调整分组数
g,可在资源受限环境(如移动端)和性能敏感场景(如模型训练)间灵活切换。
③ 长序列推理优化
- 显存占用:键值缓存(KV Cache)显存需求降为 MHA 的
g/h(例如h=8,g=2 时显存占用量为25%)。
4. 实际案例解析
案例 1:云端大模型推理
-
场景:部署千亿参数模型处理用户并发请求。
-
GQA 作用:
- 将
h=64 头分为g=8 组,显存占用减少为原来的1/8,支持更多并发。 - 推理延迟降低30%,同时保持99%的模型准确率。
- 将
案例 2:多模态模型训练
-
场景:训练同时处理文本和图像的模型(如GPT-4 Vision)。
-
GQA 作用:
- 文本层使用
g=4 组,图像层使用g=2 组,平衡不同模态的计算需求。 - 训练速度提升15%,收敛效果接近全头注意力。
- 文本层使用
5. 关键设计选择
-
分组数(g) :
- 典型值:
g=2(平衡)、g=4(高效)。 - 调整策略:模型规模越大,分组数可适当增加(如千亿模型用
g=8)。
- 典型值:
-
投影维度(d_k) :
- 可略微增加共享键值的维度(如从64增至96),补偿信息损失。
6. GQA vs. MHA vs. MQA
| 对比维度 | GQA(分组查询注意力) | MHA(多头注意力) | MQA(多查询注意力) |
|---|---|---|---|
| 键值投影 | g 组独立 | h 组独立 | 1组共享 |
| 计算开销 | 中等(键值计算量降为 g/h) | 最高 | 最低 |
| 显存占用 | 中等(显存降为 g/h) | 最高 | 最低 |
| 模型性能 | 接近MHA(损失<1%) | 最优 | 接近MHA(损失2-5%) |
| 适用场景 | 资源受限但需高精度的任务 | 训练或高精度推理 | 极致推理效率场景 |
7. GQA 的变体与优化
- 动态分组:根据输入内容动态调整分组数
g(如简单文本用g=4,复杂逻辑用g=2)。 - 跨层共享:不同Transformer层共享同一组键值投影(如底层共享,高层独立)。
- 混合分组:部分头保持独立(如保留10%的头不分组),增强关键信息捕捉能力。
总结
分组查询注意力(GQA)通过“分组共享键值”的设计,在计算效率与模型性能间找到了优雅的平衡点。它如同一个“灵活协作的团队”,既避免了重复劳动(MHA),又防止了信息过度简化(MQA),成为大模型落地应用(如GPT-4、Llama 2)中的关键技术,完美诠释了工程优化中的 “中庸之道” 。
MLA(Multi-Head Latent Attention)
多头潜在注意力(Multi-Head Latent Attention,MLA) 是 DeepSeek-V2 中提出的一种高效注意力变体,通过低秩投影与结构优化,显著减少推理时的显存占用(KV Cache)并保持模型性能。
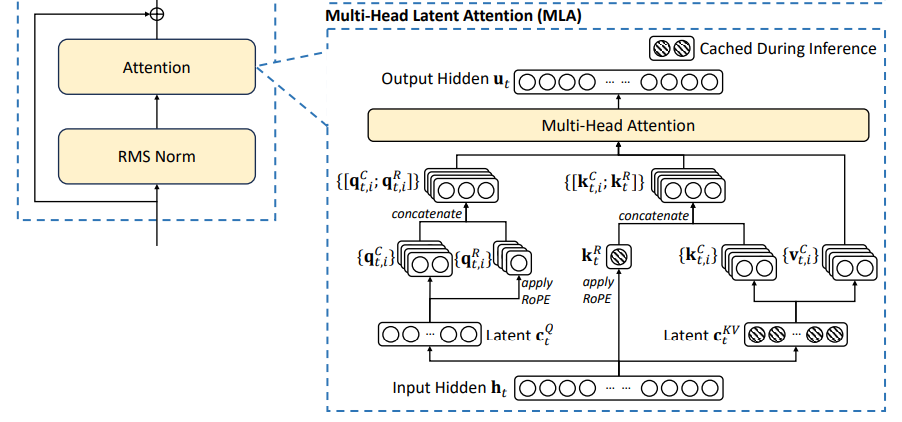
1. 核心思想:低秩投影与动态变换
-
类比:将传统的“全量信息存储”改为“压缩存储+按需解压”。如同将书籍压缩成目录(低秩投影),阅读时根据需要快速展开细节(动态变换)。
-
本质:
- 训练阶段:通过低秩投影生成中间表示(
ci),并允许不同注意力头通过独立线性变换增强表达能力。 - 推理阶段:利用注意力计算的数学特性,将多组变换等效合并,使 KV Cache 仅需存储低秩中间表示
ci,而非完整键值对。
- 训练阶段:通过低秩投影生成中间表示(
2. 具体实现步骤
以输入序列维度 (batch_size, seq_len, d_model) 为例(如 d_model=5120,头数 h=128,低秩维度 dc=512):
训练阶段
训练阶段没有什么优化的空间,正常使用低秩投影即可
-
Q矩阵通过输入信息进行低秩投影再乘以升维权重矩阵,拆为一部分为了QK的计算,一部分作为Q的旋转位置编码
python代码解读复制代码# 输入信息低秩投影后升维,Q矩阵也使用低秩矩阵是为了 q = self.wq_b(self.q_norm(self.wq_a(x))) # 拆为[没有位置编码的输入信息,需要进行旋转位置编码的输入信息] q_nope, q_pe = torch.split(q, [self.qk_nope_head_dim, self.qk_rope_head_dim], dim=-1) # Q的旋转位置编码 q_pe = apply_rotary_emb(q_pe, freqs_cis) -
计算得到KV矩阵,通过输入信息低秩投影后进行拆分,一部分作为输入投影进行QK的计算,一部分作为旋转位置编码的输入矩阵
python代码解读复制代码# 低秩投影 kv = self.wkv_a(x) # 拆为[没有位置编码的输入信息,需要进行旋转位置编码的输入信息] kv, k_pe = torch.split(kv, [self.kv_lora_rank, self.qk_rope_head_dim], dim=-1) # K的旋转位置编码 k_pe = apply_rotary_emb(k_pe.unsqueeze(2), freqs_cis) -
为了QK计算,低秩投影的K还需要进行升维,但MLA中KV的权重矩阵合并到一个矩阵中并且来自同一个KV低秩投影,需要进行拆解
python代码解读复制代码# 矩阵升维 kv = self.wkv_b(self.kv_norm(kv)) # 矩阵变换[b, s, H, qk_nope_head_dim + v_head_dim] 此时qk_nope_head_dim = v_head_dim kv = kv.view(bsz, seqlen, self.n_local_heads, self.qk_nope_head_dim + self.v_head_dim) # 矩阵切分为 K:[b, s, H, qk_nope_head_dim] 和 V:[b, s, H, v_head_dim] k_nope, v = torch.split(kv, [self.qk_nope_head_dim, self.v_head_dim], dim=-1) -
加入旋转位置编码信息
python代码解读复制代码# 拼接Q矩阵与Q旋转位置编码矩阵 q = torch.cat([q_nope, q_pe], dim=-1) # 拼接K矩阵与K旋转位置编码矩阵 k = torch.cat([k_nope, k_pe.expand(-1, -1, self.n_local_heads, -1)], dim=-1) -
KV存入缓存并计算注意力分数
python代码解读复制代码# 缓存K self.k_cache[:bsz, start_pos:end_pos] = k # 缓存V self.v_cache[:bsz, start_pos:end_pos] = v # (Q*K) / self.qk_head_dim ** -0.5 self.qk_head_dim = self.qk_nope_head_dim + self.qk_rope_head_dim scores = torch.einsum("bshd,bthd->bsht", q, self.k_cache[:bsz, :end_pos]) * self.softmax_scale # 计算Softmax Score scores = scores.softmax(dim=-1, dtype=torch.float32).type_as(x) -
注意力分数乘以矩阵V后再乘以Wo矩阵
python代码解读复制代码# Score*V x = torch.einsum("bsht,bthd->bshd", scores, self.v_cache[:bsz, :end_pos]) x = self.wo(x.flatten(2))
推理阶段
推理阶段与训练阶段不同,由于 Generation 阶段是一个Token一个Token的生成,每次生成都需要缓存之前的KV值,但过程中有以下几个问题:
-
KV Cache 优化:
如果直接缓存KV值,就和MHA一样,并没有对KV Cache的大小进行优化,这时我们可以通过一个恒等变换来规避这个问题
这样我们可以将 作为一个整体并将其视为 Q,那 可以视为 K 而存入 KV Cache,此时的 就是低秩投影后的
-
不兼容旋转位置编码(RoPE) :
这里我们可以发现 并不能成为一个固定的矩阵,其中 为位置差异,差异变化导致矩阵变化,所以DeepSeek中的做法是在推理阶段的旋转位置编码的信息没有选择拼接到QK中,而是相加,这样即融合了位置编码信息,又减少了矩阵乘法
python代码解读复制代码# 注:这里有一个细节,就是W_q^{(s)}W_k^{(s)⊤} 合并成一个矩阵的恒等变换,理论上只有在无限精度下才成立, 所以这边做去量化操作来提升精度以此来降低误差损失 wkv_b = self.wkv_b.weight if self.wkv_b.scale is None else weight_dequant(self.wkv_b.weight, self.wkv_b.scale, block_size) # [n_local_heads * qk_nope_head_dim, kv_lora_rank] => [n_local_heads, qk_nope_head_dim, kv_lora_rank] wkv_b = wkv_b.view(self.n_local_heads, -1, self.kv_lora_rank) # 计算不带位置编码的q q_nope = torch.einsum("bshd,hdc->bshc", q_nope, wkv_b[:, :self.qk_nope_head_dim]) # 缓存KV Cache 和 RoPE Cache self.kv_cache[:bsz, start_pos:end_pos] = self.kv_norm(kv) self.pe_cache[:bsz, start_pos:end_pos] = k_pe.squeeze(2) # (q(w_qw_k)c_i + q_pe*k_pe) / self.qk_head_dim ** -0.5 scores = (torch.einsum("bshc,btc->bsht", q_nope, self.kv_cache[:bsz, :end_pos]) + torch.einsum("bshr,btr->bsht", q_pe, self.pe_cache[:bsz, :end_pos])) * self.softmax_scale
3. 为什么需要MLA?
① 极致压缩KV Cache
-
显存对比:
- MHA:存储
h 组独立键值 → 显存占用高。 - GQA:存储
g 组键值 → 显存减少为1/g。 - MLA:仅存储低秩中间表示
ci → 显存占用 低于GQA(DeepSeek-V2 中dc=512,远小于g*(dk+dv))。
- MHA:存储
② 兼容RoPE位置编码
-
问题:传统低秩投影与 RoPE 的旋转矩阵冲突,导致位置信息丢失。
-
解决方案:
- 将 RoPE 仅应用于部分新增维度(
dr=64),保持主要维度兼容低秩变换。 - 所有头共享 RoPE 相关投影,避免显存膨胀。
- 将 RoPE 仅应用于部分新增维度(
③ 平衡训练与推理效率
- 训练阶段:通过低秩投影减少参数量和梯度显存(如
d'c=1536 的中间维度)。 - 推理阶段:等效变换保持计算逻辑,利用带宽优化加速生成。
4. 实际案例解析
案例 1:长文本生成
-
场景:生成 1000 Token 的小说章节。
-
MLA 作用:
- KV Cache 显存从 24GB(MHA)降至 1.5GB(MLA),允许在消费级显卡运行。
- 生成速度提升 2 倍(带宽瓶颈缓解)。
案例 2:多轮对话系统
-
场景:处理 10 轮历史对话(每轮 200 Token)。
-
MLA 作用:
- 历史对话的 KV Cache 可全部存入显存,避免频繁卸载到内存。
- 响应延迟从 500ms 降至 200ms。
5. 关键设计选择
| 参数 | 典型值 | 作用 |
|---|---|---|
| 低秩维度 dc | 512 | 平衡信息压缩率与性能损失 |
| RoPE 维度 dr | 64 | 保留足够位置信息,避免语义混淆 |
| 查询投影 d'c | 1536 | 增强查询表达能力,补偿低秩信息损失 |
| 头数 h | 128 | 通过增加头数提升模型容量,不增加显存 |
6. MLA vs. GQA vs. MQA
| 对比维度 | MLA | GQA | MQA |
|---|---|---|---|
| KV Cache 大小 | 最小(仅存 ci) | 中等(存 g 组键值) | 最小(存 1 组键值) |
| 模型容量 | 最高(头数可自由扩展) | 中等(受分组数限制) | 最低(键值完全共享) |
| RoPE 兼容性 | 部分兼容(新增 RoPE 维度) | 完全兼容 | 完全兼容 |
| 适用场景 | 超长序列、高并发推理 | 通用任务 | 极致轻量级部署 |
7. MLA 流程图理解
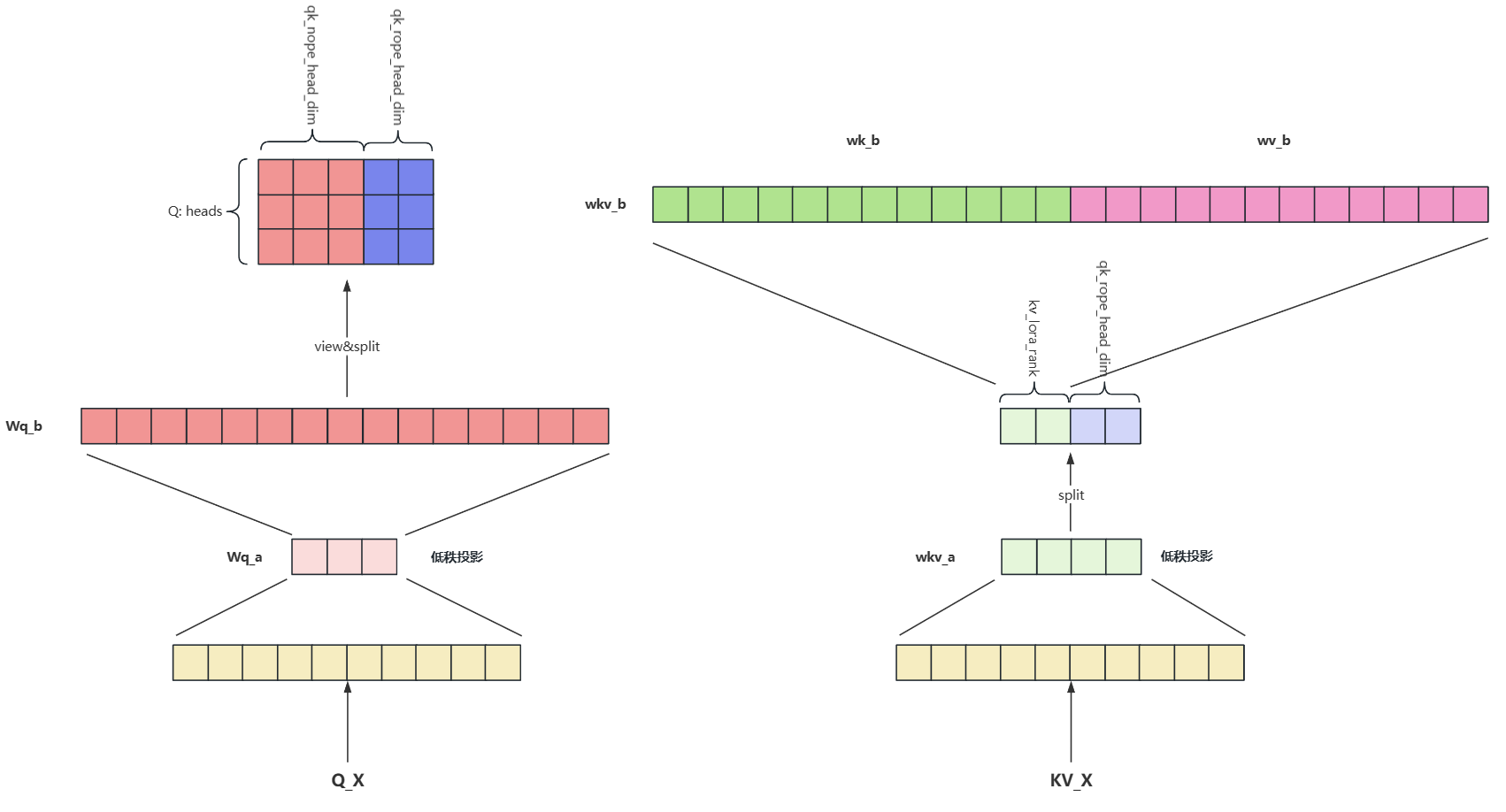
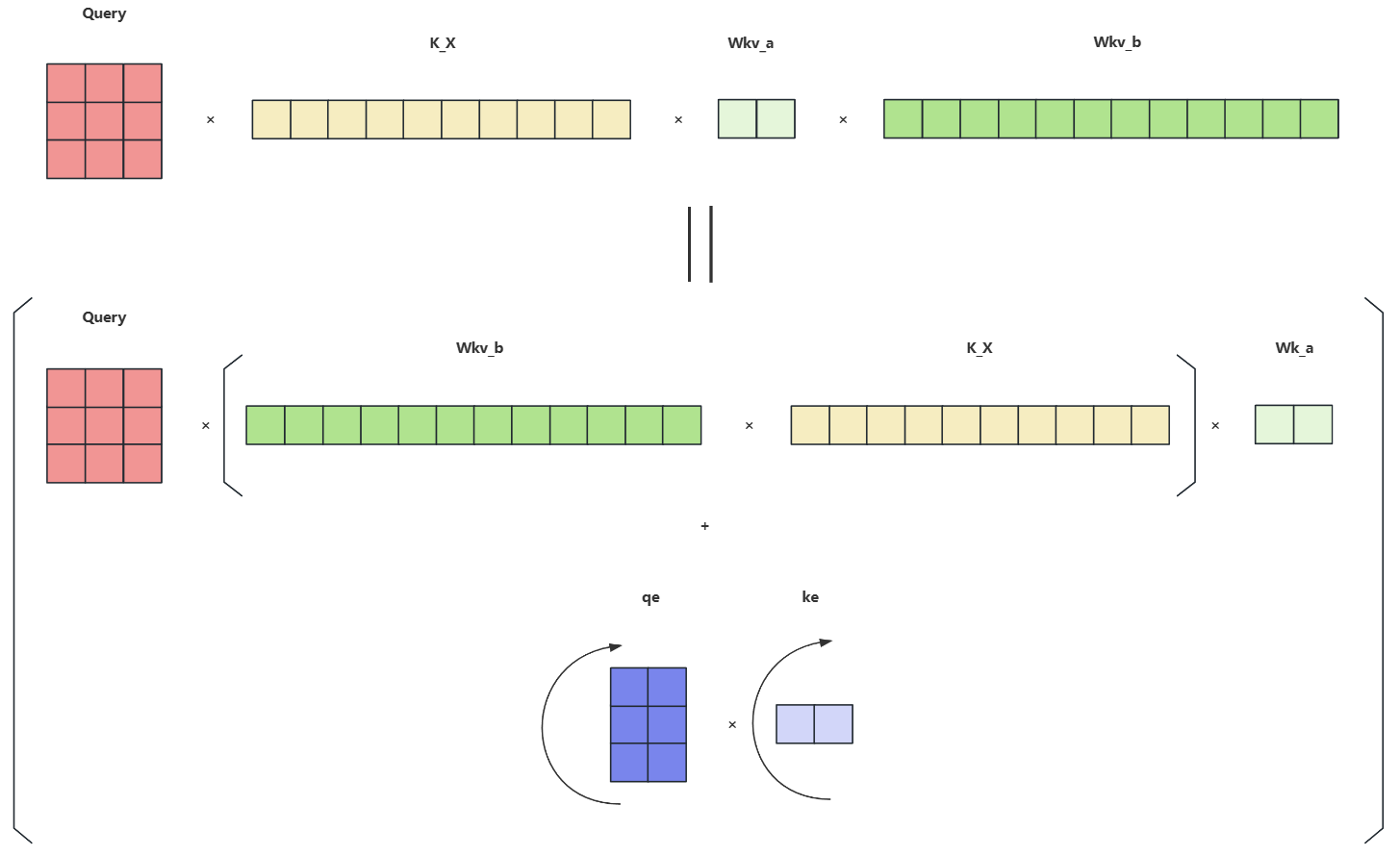
8. MLA 代码实现
其中torch.einsum()的使用技巧:torch.einsum()1
python 代码解读复制代码def rotate_half(x):
x1, x2 = x.chunk(2, dim=-1)
return torch.cat((-x2, x1), dim=-1)
def apply_rotate_pos_emb(q, k, cos, sin, unsqueeze_dim=2):
cos = cos.unsqueeze(unsqueeze_dim)
sin = sin.unsqueeze(unsqueeze_dim)
q_embed = (q * cos) + (rotate_half(q) * sin)
k_embed = (k * cos) + (rotate_half(k) * sin)
return q_embed, k_embed
# 旋转位置编码
class RotaryEmbedding(nn.Module):
def __init__(self, dim, max_seq_len=1024):
super(RotaryEmbedding, self).__init__()
self.dim = dim
self.max_seq_len = max_seq_len
inv_freq = 1.0 / (10000 ** (torch.arange(0, dim, 2).float() / dim))
t = torch.arange(max_seq_len).float().unsqueeze(1)
freqs = t @ inv_freq.unsqueeze(0)
freqs = torch.cat((freqs, freqs), dim=-1)
self.register_buffer("cos_cached", freqs.cos())
self.register_buffer("sin_cached", freqs.sin())
def forward(self, q, k):
cos = self.cos_cached[:q.shape[1], :].unsqueeze(0)
sin = self.sin_cached[:q.shape[1], :].unsqueeze(0)
return apply_rotate_pos_emb(q, k, cos, sin)
python 代码解读复制代码class MLA(nn.Module):
def __init__(self,
dim,
n_heads,
q_lora_rank,
kv_lora_rank,
qk_nope_head_dim,
qk_rope_head_dim,
v_head_dim,
max_seq_len,
max_batch_size,
mode):
super().__init__()
self.dim = dim # 隐藏层维度
self.n_heads = n_heads #总头数
self.q_lora_rank = q_lora_rank # q低秩压缩到的维度
self.kv_lora_rank = kv_lora_rank # kv低秩压缩到的维度
self.qk_nope_head_dim = qk_nope_head_dim
self.qk_rope_head_dim = qk_rope_head_dim
self.qk_head_dim = qk_nope_head_dim + qk_rope_head_dim # qk的总维度,不带旋转位置编码的维度加上带旋转位置编码的维度
self.v_head_dim = v_head_dim # value的维度,等于不带旋转位置编码的k维度
self.mode = mode
self.max_seq_len = max_seq_len
self.max_batch_size = max_batch_size
self.wq_a = nn.Linear(self.dim, self.q_lora_rank) # q的降维矩阵
self.q_norm = RMSNorm(self.q_lora_rank)
self.wq_b = nn.Linear(self.q_lora_rank, self.n_heads * self.qk_head_dim) # q的升维矩阵
# 4096*128+128*4864 = 524,288 + 622592 = 1146880 4096*4864 = 19,922,944
self.wkv_a = nn.Linear(self.dim, self.kv_lora_rank + self.qk_rope_head_dim) # kv的降维矩阵
# nn.Linear(self.dim, self.kv_lora_rank)
# nn.Linear(self.dim, self.qk_rope_head_dim)
self.kv_norm = RMSNorm(self.kv_lora_rank)
self.wkv_b = nn.Linear(self.kv_lora_rank, self.n_heads * (self.qk_nope_head_dim + self.v_head_dim)) # kv的升维矩阵
self.wo = nn.Linear(self.n_heads * self.v_head_dim, self.dim)
self.rotary_emb = RotaryEmbedding(self.qk_rope_head_dim) # 旋转旋转位置编码
if self.mode == 'naive':
self.register_buffer('k_cache', torch.zeros(self.max_batch_size, self.max_seq_len, self.n_heads, self.qk_head_dim), persistent=False)
self.register_buffer('v_cache', torch.zeros(self.max_batch_size, self.max_seq_len, self.n_heads, self.v_head_dim), persistent=False)
else:
self.register_buffer('kv_cache', torch.zeros(self.max_batch_size, self.max_seq_len, self.kv_lora_rank), persistent=False)
self.register_buffer('pe_cache', torch.zeros(self.max_batch_size, self.max_seq_len, self.qk_rope_head_dim), persistent=False)
def forward(self, x, mask=None):
bs, seq_len, _ = x.shape
q = self.wq_a(x) # [bs, seq_len, q_lora_rank]
q = self.q_norm(q) # [bs, seq_len, q_lora_rank]
q = self.wq_b(q) # [bs, seq_len, n_heads * qk_head_dim]
q = q.view(bs, seq_len, self.n_heads, self.qk_head_dim) # [bs, seq_len, n_heads, qk_head_dim]
q_nope, q_pe = torch.split(q, [self.qk_nope_head_dim, self.qk_rope_head_dim], dim=-1) # q_nope shape:[bs, seq_len, n_heads, qk_nope_head_dim] q_pe shape:[bs, seq_len, n_heads, qk_rope_head_dim]
kv = self.wkv_a(x) # [bs, seq_len, kv_lora_rank + qk_rope_head_dim]
kv, k_pe = torch.split(kv, [self.kv_lora_rank, self.qk_rope_head_dim], dim=-1) # kv shape:[bs, seq_len, kv_lora_rank] k_pe shape:[bs, seq_len, qk_rope_head_dim]
k_pe = k_pe.unsqueeze(2) # k_pe shape:[bs, seq_len, 1, qk_rope_head_dim]
q_pe, k_pe = self.rotary_emb(q_pe, k_pe)
if self.mode == 'naive':
q = torch.cat([q_nope, q_pe], dim=-1) # * [bs, seq_len, n_heads, qk_head_dim]
kv = self.kv_norm(kv) # [bs, seq_len, kv_lora_rank)]
kv = self.wkv_b(kv) # [bs, seq_len, n_heads * (qk_nope_head_dim + v_head_dim)]
kv = kv.view(bs, seq_len, self.n_heads, self.qk_nope_head_dim + self.v_head_dim)
k_nope, v = torch.split(kv, [self.qk_nope_head_dim, self.v_head_dim], dim=-1)
k = torch.cat([k_nope, k_pe.expand(-1,-1,self.n_heads,-1)], dim=-1)
# k shape:[bs, seq_len, n_heads, qk_head_dim]
self.k_cache[:bs, :seq_len, :, :] = k
self.v_cache[:bs, :seq_len, :, :] = v
# scores = torch.einsum("bshd,bthd->bsht", q, self.k_cache[:bs, :seq_len]) / math.sqrt(self.qk_nope_head_dim + self.qk_rope_head_dim)
scores = torch.matmul(q.transpose(1, 2), self.k_cache[:bs, :seq_len, :, :].transpose(1, 2).transpose(2, 3) / math.sqrt(self.qk_nope_head_dim + self.qk_rope_head_dim))
scores = scores.transpose(1, 2)
else:
k_pe = k_pe.squeeze(2)
wkv_b = self.wkv_b.weight # [n_heads * (qk_nope_head_dim + v_head_dim), kv_lora_rank]
wkv_b = wkv_b.view(self.n_heads, -1, self.kv_lora_rank) # [n_heads, qk_nope_head_dim + v_head_dim, kv_lora_rank]
q_nope = torch.einsum("bshd,hdc->bshc", q_nope, wkv_b[:, :self.qk_nope_head_dim]) # q_nope shape:[bs, seq_len, n_heads, kv_lora_rank]
# q*k(T) = x*wq*(c*wkv_b[:, :self.qk_nope_head_dim])(T) = x*wq*wkv_b[:, :self.qk_nope_head_dim](T)*c(T) c为压缩后的kv
# wq*wkv_b[:, :self.qk_nope_head_dim](T)作为q的投影矩阵 c可以替代原先的k,这样就可以直接使用压缩后的kv计算注意力了,kv_caceh时也只需存储压缩后的kv
kv = self.kv_norm(kv)
self.kv_cache[:bs, :seq_len, :] = kv # kv shape:[bs, seq_len, kv_lora_rank]
self.pe_cache[:bs, :seq_len, :] = k_pe # k_pe shape:[bs, seq_len, qk_rope_head_dim]
scores_nope = torch.einsum("bshc,btc->bsht", q_nope, self.kv_cache[:bs, :seq_len, :]) # bshc btc -> bshc bct -> bsht
scores_pe = torch.einsum("bshr,btr->bsht", q_pe, self.pe_cache[:bs, :seq_len, :]) # bshr btr -> bshr bt1r -> bshr bthr -> bsht
scores = (scores_nope + scores_pe) / math.sqrt(self.qk_nope_head_dim + self.qk_rope_head_dim) # [bs, seq_len, n_heads, seq_len]
if mask is not None:
# mask shape:[bs, seq_len, seq_len]
scores += mask.unsqueeze(2)
scores = scores.softmax(dim=-1)
if self.mode == 'naive':
x = torch.einsum("bsht,bthd->bshd", scores, self.v_cache[:bs, :seq_len]) # bsht,bthd -> bhst, bhtd -> bhsd -> bshd
else:
# scores * v = scores * c * wkv_b[:, -self.v_head_dim:]
x = torch.einsum("bsht,btc->bshc", scores, self.kv_cache[:bs, :seq_len]) # x shape:[bs, seq_len, n_heads, kv_lora_rank]
x = torch.einsum("bshc,hdc->bshd", x, wkv_b[:, -self.v_head_dim:]) # bshc, hdc -> bshc,dch -> bsdh -> bshd
x = x.contiguous ().view(bs, seq_len, -1)
x = self.wo(x)
return x
Flash Attention
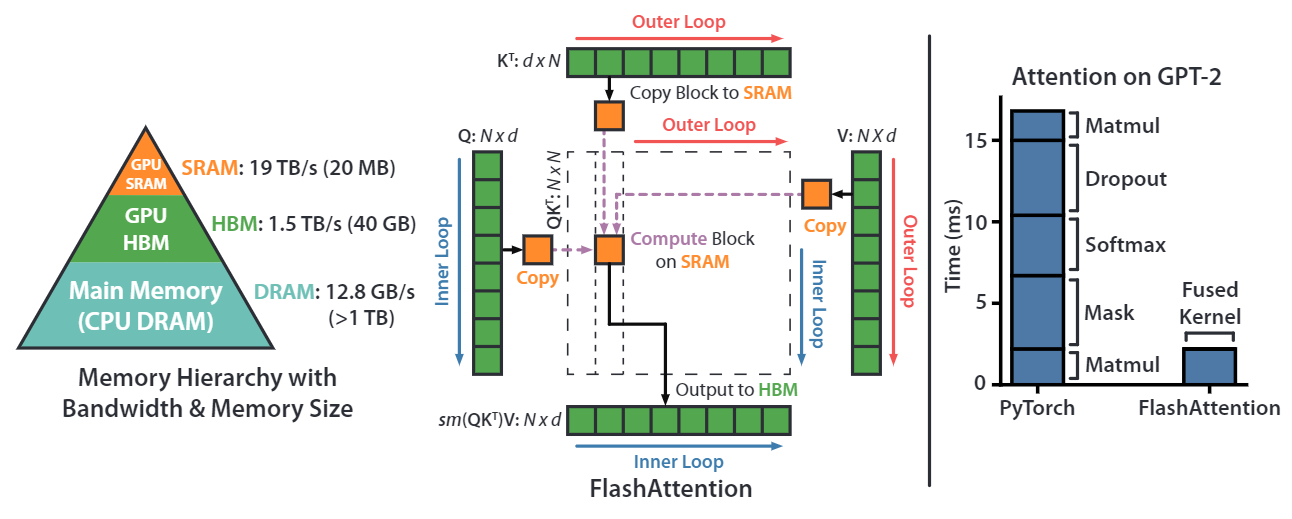
Flash Attention 是一种高效计算注意力机制的算法,由 Tri Dao 等人在 2022 年提出。它通过优化内存访问和计算模式,显著提升了注意力计算的速度并降低了显存占用,尤其在处理长序列时效果显著。
关键问题
-
传统的Attention的实现(矩阵 Q、K、V存储在 HBM(High Bandwidth Memory) 中):
- 从 HBM 加载 Q、K 到SRAM
- 计算出 S=QK^T
- 将 S 写到 HBM 中
- 将 S 加载到 SRAM 中
- 计算 P = Softmax(S)
- 将 P 写入 HBM 中
- 从 HBM 加载 P 和 V 到 SRAM
- 计算 O = PV
- 把 O 写出到 HBM
- 返回 O
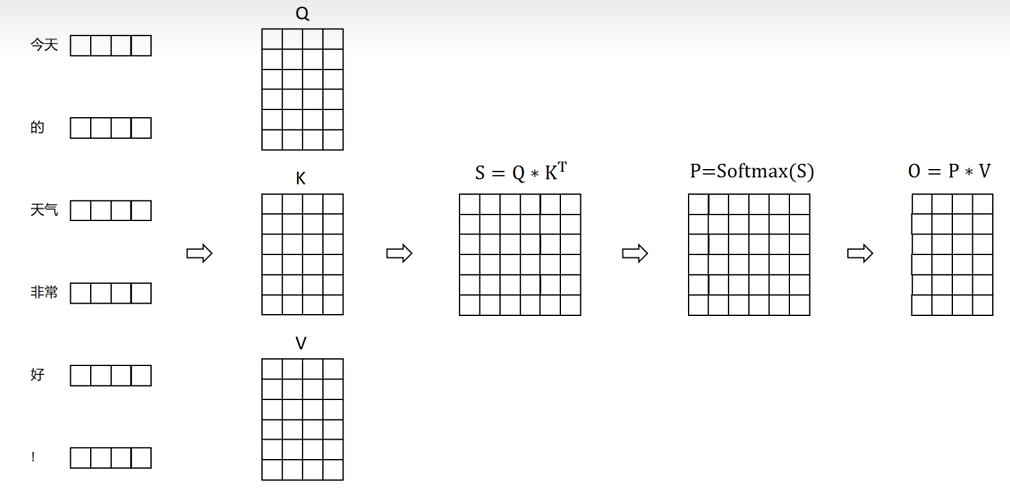
从计算过程可以发现,随着序列长度 的增长,缓存 的增长,且训练过程中的中间计算需要保存以便反向传播时进行计算,所以这部分也会占用很大的显存,并且频繁的读写 HBM 也会带来大量的 IO 消耗。
问题分析
在 Attention 计算的性能表现上主要又两个瓶颈:计算瓶颈(Compute-Bound)和显存瓶颈(Memory-Bound)
- 计算瓶颈:大矩阵的乘法(Matmul),或者是多Channel的卷积操作
- 显存瓶颈:按位操作(Relu,Dropout...),规约操作(sum,Softmax...)
在消耗时间上来看,矩阵乘法并非主要耗时原因,更多还是在 Memory-Bound 上体现:
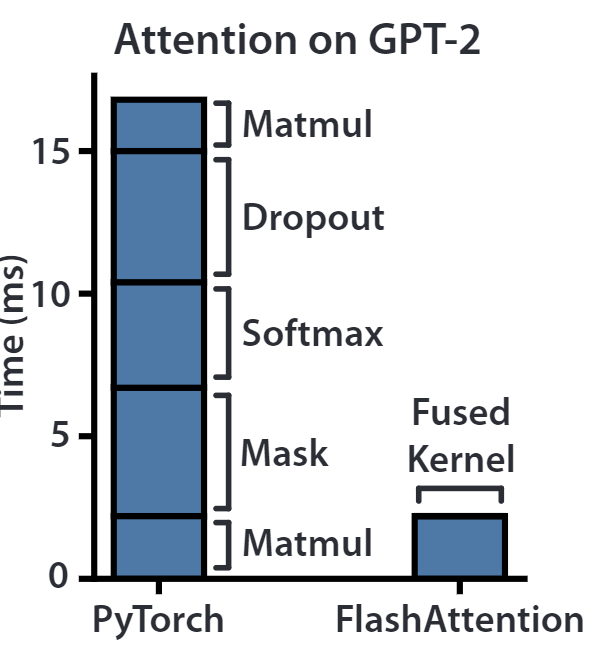
另外,之前对于 Attention 的优化都是在提高计算速度上,而 Flash Attention 更加着眼于提高 IO 效率上,比如 HBM 的读写速度远远小于 SRAM 的读写效率,所以我们希望尽可能的让数据读写向 SRAM 靠拢,减少对于 HBM 的读写。
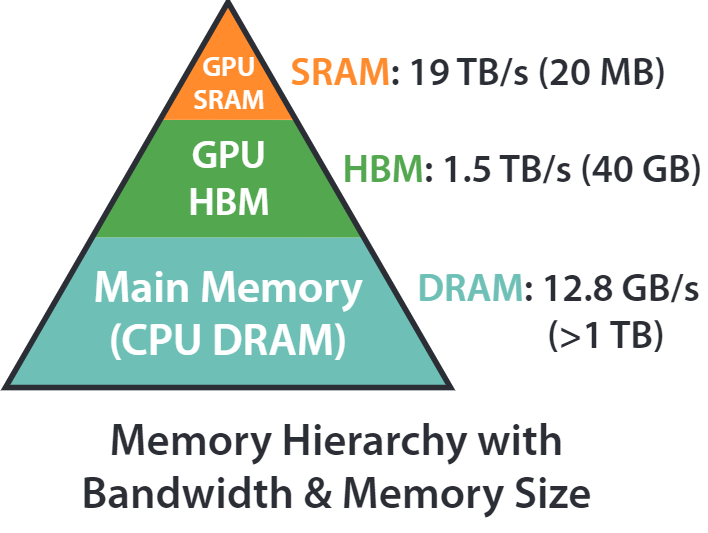
问题解决
解决思路
目标:避免 Attention Matrix 从 HBM 的读写
-
通过分块计算,融合(Fusion 操作)多个计算过程,减少中间结果缓存
- QKVO四个矩阵存入HBM中
- 将QKV 进行分块
- 将 KV矩阵块 作为外循环进行遍历,Q 矩阵块作为内循环进行遍历
- QK子块相乘后的结果不缓存中间结果直接进行Softmax分块计算再乘以 V 子块,得到局部权重 O‘
- 更新矩阵 O
-
反向传播时,重新计算中间结果。
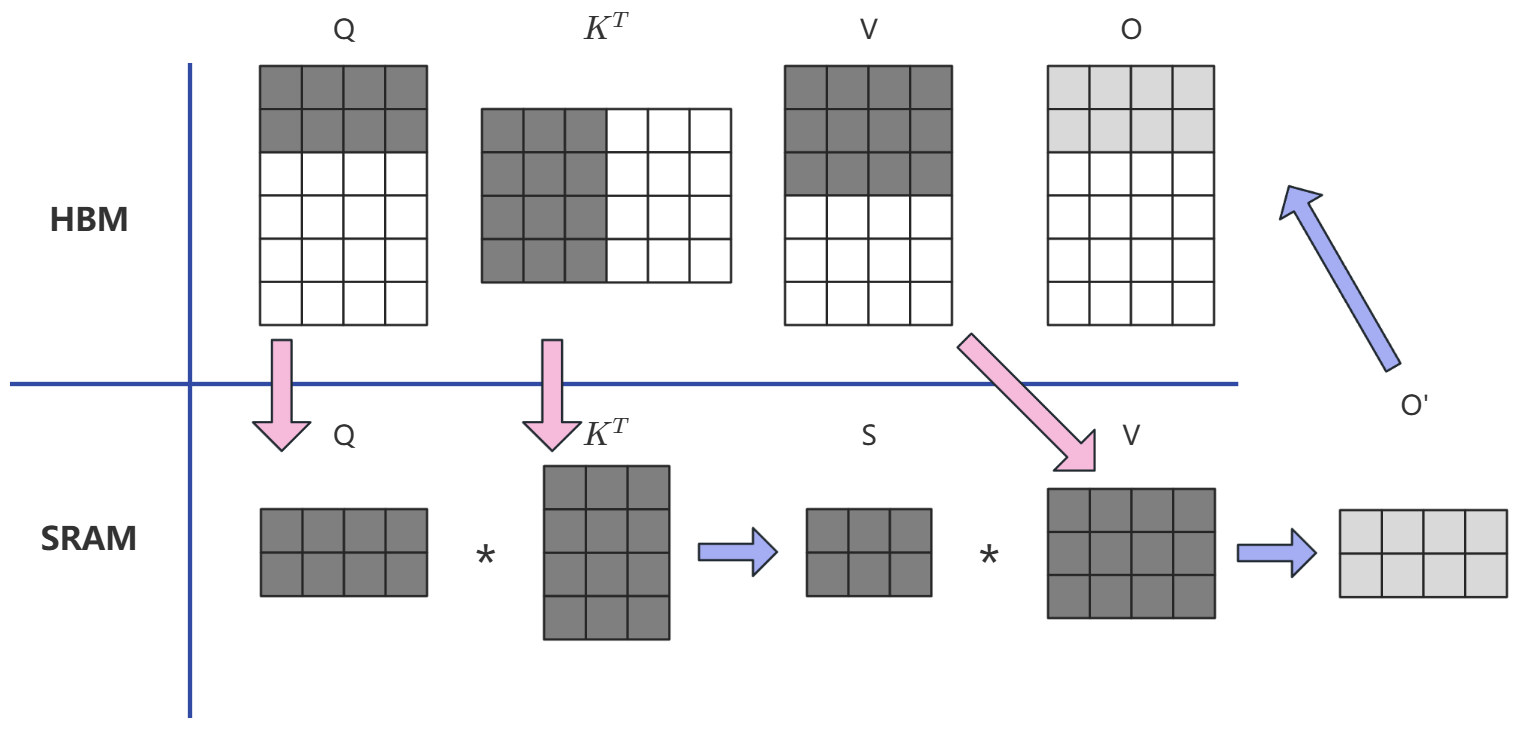
Softmax分块计算
问题:Softmax也需要计算融合,如何进行分块计算呢?
首先当前大模型使用的精度多为混合精度 FP16 下进行训练,最大表示65536,明显超过了其最大值,所有我们需要使用safe_softmx,额外需要注意的是,softmax必需在 整行数据都计算好之后才可参与计算。
-
Safe Softmax原始公式
-
对上述公式进行拆解:
-
分块计算获得对应快的,,,,, 略:
-
计算Softmax 还需要从分块中的局部最大值找到全局最大值并作用在全局中,通过 补全差异:
Flash Attention 计算流程

-
初始化:
-
设置块大小 ,。
- 列块****:列块大小设置为(),这里的“4”表示要存储QKVO四个矩阵块。这里提到的 和 分别代表列块和行块的大小。
- 行块****:取 和 的最小值是为了防止行维度过长导致中间计算结果的矩阵过大而超出SRAN的内存大小
-
初始化矩阵 ,向量 ,和向量 。创建一个用于存放最终结果的空间,它们在后续步骤中用来帮助计算。
-
-
划分矩阵:
- 将查询矩阵 划分为 个块 ,每个块的大小为 。
- 将键矩阵 和值矩阵 划分为 个块 和 ,每个块的大小为 。
- 原始的大矩阵(查询 、键 、值 )被切分成多个小块。这样做是为了让这些数据块能够更好地适应GPU或TPU等硬件上的快速访问存储(SRAM),从而提高计算效率。
-
迭代处理:
-
对于每个键矩阵块 和值矩阵块 :
-
从HBM加载 和 到片上SRAM。
-
对于每个查询矩阵块 :
- 从HBM加载 ,,, 到片上SRAM。
- 在片上计算注意力得分矩阵 。
- 计算行最大值 ,并进行归一化得到 。
- 更新 和 。
- 更新输出矩阵 并写回HBM。
-
-
-
返回结果:
- 返回最终的输出矩阵 。
在 Flash Attention 的伪代码中,第 12 步是算法实现中的一个关键操作,涉及如何将当前分块(Tile)的局部计算结果与全局输出进行融合。以下是该步骤的详细解释:
伪代码第 12 步解读
在 Flash Attention 的分块计算流程中:
- 输入分块:将查询(Q)、键(K)、值(V)矩阵分割为较小的块(Tile)。
- 局部注意力计算:在高速缓存(如 GPU SRAM)中计算当前块的注意力权重和输出。
- 全局结果更新:将局部结果与全局输出结合,同时维护数值稳定性(如 softmax 归一化的分母)。
第 12 步的具体操作(以论文中的符号为例):
这一公式的作用是:将当前块的注意力输出 与之前累积的全局输出 合并,并调整归一化因子以保持数值稳定。
分步解释
1. 符号定义
- :全局输出矩阵的第 个块(最终输出的一部分)。
- :累积的归一化分母(用于 softmax 的分母,初始化为 0)。
- :当前块的最大指数值(用于数值稳定性)。
- :当前块的局部注意力权重(未归一化的 )。
- :值矩阵的第 个块。
2. 公式拆解
- :调整因子,用于对齐新旧块的最大指数值,防止数值溢出。
- :将之前累积的输出 按新的最大指数值 重新缩放。
- :将当前块的局部输出 按新的最大指数值缩放。
- :用更新后的归一化分母 对合并后的结果进行归一化。
3. 数学意义
-
在线 softmax 调整: 由于分块计算时每个块的最大指数值 不同,直接合并会导致数值不稳定(如指数爆炸)。通过动态调整新旧块的最大值差异(),确保所有中间结果在同一尺度下融合。
-
归一化分母更新: ,最终用 归一化输出,保证 softmax 的正确性。
-
为什么使用****:
等价于 的每行乘以 的对应元素,softmax 的分母是逐行计算的(每个 token 对其他 token 的注意力权重归一化)。因此,调整历史输出和归一化时,必须保证每行的缩放和归一化独立进行。【2,3】
直观理解
假设我们要计算两个分块的结果:
-
第一个块:最大指数值为 ,计算局部输出 和分母 。
-
第二个块:最大指数值为 (可能大于 )。
- 调整历史输出:将 按 缩小,避免新块的最大值 导致溢出。
- 合并新结果:将当前块的输出 按 缩放后加入。
- 更新分母:用新的分母 归一化合并后的输出。
这种动态调整机制是 Flash Attention 实现高效且数值稳定的关键!
实际代码示例(简化版)
python 代码解读复制代码# 假设当前块的最大值为 m_new,历史最大值为 m_old
scale_old = np.exp(m_old - m_new) # 历史输出的缩放因子
scale_current = np.exp(m_current - m_new) # 当前块的缩放因子
# 合并输出:调整历史输出 + 当前块输出
O_i = (scale_old * O_i_prev + scale_current * P_ij_Vj) / l_i_new
Flash Attention V2
以下是FlashAttention-2的核心内容总结及其相对于FlashAttention-1的主要改进,结合论文及实际应用分析:
FlashAttention-1的核心原理与局限性
-
核心思想 FlashAttention-1通过分块(Tiling) 和重计算(Recomputation) 优化注意力计算:
- 将输入矩阵(Q、K、V)分块加载到GPU的SRAM中,避免存储中间注意力矩阵(如Softmax结果),将内存占用从降至。
- 通过动态调整Softmax的归一化因子(最大值和分母),实现数值稳定性。
-
局限性
- 计算效率不足:仅达到GPU理论最大FLOPs/s的25-40%(如A100的124 TFLOPs/s),远低于优化矩阵乘法(GEMM)的80-90%。
- 并行性不足:仅在批次(batch)和注意力头(head)维度并行,未充分利用长序列的并行潜力。
- 共享内存读写开销:线程块(thread block)内不同线程束(warp)需频繁同步中间结果,导致性能瓶颈。
以下是FlashAttention-2相对于FlashAttention-1的主要改进点及其详细技术解析,结合算法设计、硬件适配和实验结果:
1. 减少非矩阵乘法运算(Non-Matmul FLOPs)
问题背景
- GPU计算特性:现代GPU(如NVIDIA A100)的矩阵乘法单元(Tensor Core)理论吞吐量高达312 TFLOPs/s,而其他操作(如指数、求和、除法等“非矩阵乘法运算”)的吞吐量仅19.5 TFLOPs/s。每个非矩阵FLOP的实际计算成本是矩阵乘法的16倍。
- FlashAttention-1的瓶颈:
FlashAttention-1中,非矩阵运算占整体计算量的约30%,尤其是动态调整Softmax的缩放因子(如重缩放
e^{m_i - m_new})和边界检查操作(如NaN检测)。
FlashAttention-2的优化

-
Softmax计算重构: 将FlashAttention-1中的两次缩放(一次对齐最大值,一次归一化分母)合并为单次缩放,减少50%的非矩阵运算。 具体步骤:
- 在分块计算时,直接使用全局最大值对齐局部结果,避免中间重缩放。
- 仅需在最终归一化时进行一次除法,而非多次逐块调整。
-
硬件感知优化: 将非矩阵运算(如指数、求和)尽可能融合到矩阵乘法计算中,利用GPU的指令级并行(ILP)隐藏延迟。 例如:在计算
QK^T时,同步执行局部最大值(max)和指数求和(sum)。
效果
- 非矩阵运算占比从30%降至15%,整体计算速度提升20-30%。
- 在A100 GPU上,前向传播的矩阵乘法利用率(MFU)从40%提升至73%。
2. 改进并行策略
问题背景
- FlashAttention-1的并行性局限: 仅在批次(batch)和注意力头(head)维度并行,当处理长序列(如16K tokens)且batch_size或head数较小时,GPU线程利用率不足(如仅占用30%计算单元)。
FlashAttention-2的优化
-
新增序列维度并行: 将长序列划分为多个子块(例如每个子块256 tokens),在不同GPU线程块(thread block)上并行处理这些子块。 示例:
- 输入序列长度N=16K → 划分为64个子块(每个256 tokens)。
- 每个子块分配独立的线程块,充分利用GPU的SM(Streaming Multiprocessor)。
-
前向传播循环顺序调整: FlashAttention-1的外层循环遍历K/V块,内层循环遍历Q块,导致中间结果需频繁写回HBM(高带宽内存)。 FlashAttention-2改为外层循环遍历Q块,内层遍历K/V块,使输出矩阵O始终驻留在SRAM中,减少HBM访问次数。
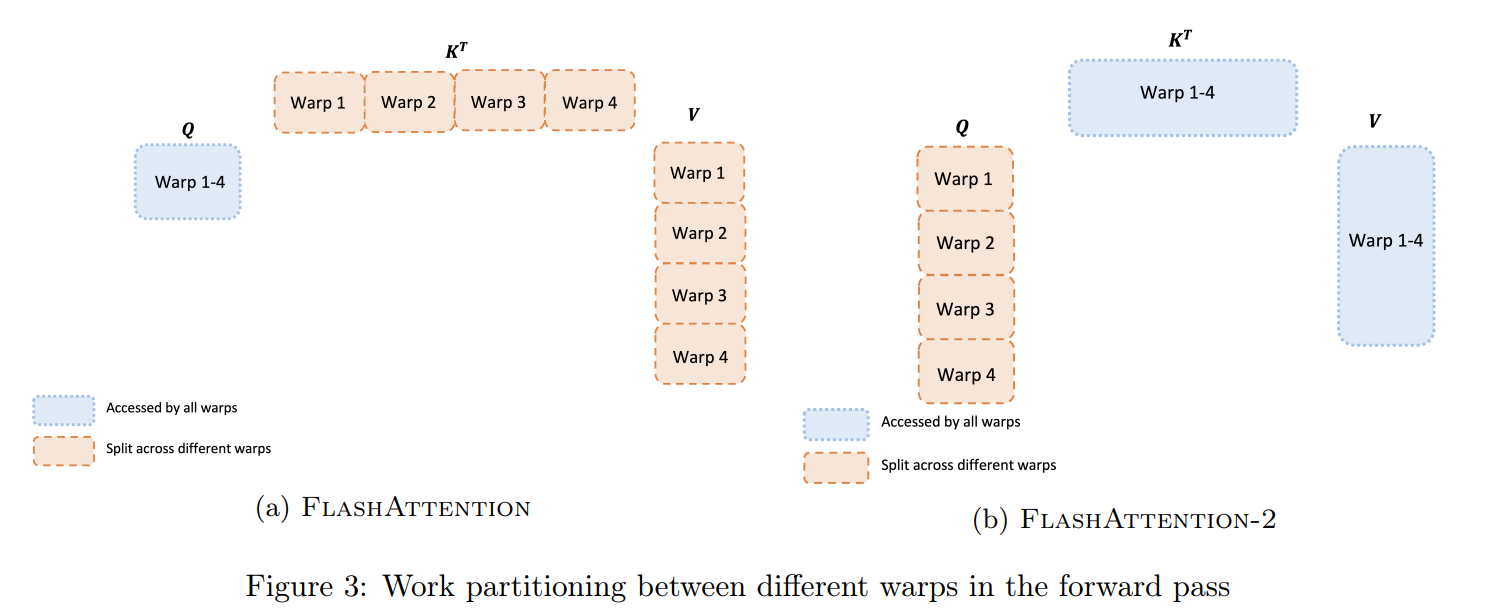
效果
- 在长序列场景(如N=16K)下,GPU利用率从30%提升至80%。
- 显存访问量减少50%,计算速度提升1.5-2倍。
3. 优化线程块内的工作分区(Work Partitioning)
问题背景
- FlashAttention-1的线程块设计: 将K和V的块分配到不同线程束(warp),每个warp独立计算局部QK^T和PV,需频繁同步中间结果(如局部最大值和分母)。 导致共享内存(shared memory)的读写竞争和同步开销。
FlashAttention-2的优化
-
统一K/V共享,分块处理Q:
- 每个线程块(thread block)加载完整的K和V块到共享内存。
- 将Q块划分为多个子块,分配到同一线程块内的不同warp。
- 所有warp共享相同的K/V,无需同步中间结果。
效果
- 共享内存的读写冲突减少70%,同步开销降低。
- 单个线程块的计算速度提升40%。
4. 支持新功能与扩展性
(1) 支持更大的头维度(Head Dimension)
- 背景: FlashAttention-1仅支持头维度≤128,无法适配GPT-J(头维度256)或Stable Diffusion(头维度160)等模型。
- 改进: 重构矩阵分块策略,允许头维度扩展至256,兼容更多模型架构。
(2) 多查询注意力(MQA)与分组查询注意力(GQA)
- 背景: MQA/GQA通过共享键(K)和值(V)的投影矩阵,减少推理时的KV缓存大小(例如从70GB→4GB)。
- 改进: 优化K/V的内存访问模式,支持同一批次内不同查询头共享K/V块,提升推理吞吐量30%。
5. 性能对比与实验结果
| 指标 | FlashAttention-1 | FlashAttention-2 |
|---|---|---|
| 前向传播速度(TFLOPs/s) | 124 | 230 |
| 训练速度(模型FLOP利用率) | 40% | 72% |
| 最大支持序列长度 | 16K tokens | 32K tokens |
| 多查询注意力支持 | 不支持 | 支持(MQA/GQA) |
Footnotes
-
torch.einsum()
torch.einsum() 是 PyTorch 中一个强大的张量操作函数,基于爱因斯坦求和约定(Einstein Summation Convention),可以高效实现复杂的张量乘积、转置、求和等操作。它通过简明的符号语法描述多维张量间的运算逻辑,是处理高维张量时的利器。
基本语法
python代码解读复制代码torch.einsum("表达式", 张量1, 张量2, ...)-
表达式:用逗号分隔输入张量的维度标记,箭头
-> 后接输出张量的维度标记。 -
规则:
- 输入张量的维度标记用字母(如
i, j, k)表示。 - 重复的字母表示对应维度需要求和(类似矩阵乘法的行×列求和)。
- 输出维度由箭头后的字母顺序决定。
- 输入张量的维度标记用字母(如
常见用法示例
1. 矩阵乘法(Matrix Multiplication)
python代码解读复制代码A = torch.randn(3, 4) B = torch.randn(4, 5) # 矩阵乘法: C = A @ B C = torch.einsum("ik,kj->ij", A, B) # 等价于 torch.matmul(A, B)-
ik 对应A 的维度(3,4),kj 对应B 的维度(4,5)。 -
k 是重复的维度,会被求和,结果维度为ij →(3,5)。
2. 向量点积(Dot Product)
python代码解读复制代码a = torch.randn(5) b = torch.randn(5) # 点积: sum(a_i * b_i) c = torch.einsum("i,i->", a, b) # 等价于 torch.dot(a, b)- 重复的
i 被求和,输出无维度(标量)。
3. 张量缩并(Tensor Contraction)
python代码解读复制代码A = torch.randn(2, 3, 4) B = torch.randn(4, 5) # 缩并 A 的第3维与 B 的第1维 C = torch.einsum("ijk,kl->ijl", A, B) # 输出形状 (2,3,5)-
k 被求和,输出维度ijl →(2,3,5)。
4. 批量矩阵乘法(Batch Matrix Multiplication)
python代码解读复制代码A = torch.randn(10, 3, 4) # 批量大小 10 B = torch.randn(10, 4, 5) # 批量矩阵乘法: C[b,i,j] = sum_k A[b,i,k] * B[b,k,j] C = torch.einsum("bik,bkj->bij", A, B) # 输出形状 (10,3,5)- 批量维度
b 被保留,k 被求和。
5. 对角线求和(Trace)
python代码解读复制代码A = torch.randn(5, 5) # 求矩阵的迹: sum(A[i,i]) trace = torch.einsum("ii->", A) # 等价于 torch.trace(A)
6. 转置(Transpose)
python代码解读复制代码A = torch.randn(3, 4) # 转置 A A_T = torch.einsum("ij->ji", A) # 等价于 A.permute(1,0)
高阶用法
1. 广播机制(Broadcasting)
python代码解读复制代码A = torch.randn(3, 4) B = torch.randn(5, 4) # 广播乘法: A 扩展为 (5,3,4), B 扩展为 (5,3,4) C = torch.einsum("ij,kj->ikj", A, B) # 输出形状 (5,3,4)2. 外积(Outer Product)
python代码解读复制代码a = torch.randn(3) b = torch.randn(4) # 外积: C[i,j] = a[i] * b[j] C = torch.einsum("i,j->ij", a, b) # 等价于 torch.outer(a, b)
注意事项
- 维度匹配:输入张量的对应维度必须一致(除非使用广播)。
- 性能:虽然
einsum 灵活,但某些操作(如矩阵乘法)直接使用torch.matmul 可能更高效。 - 可读性:复杂的表达式可能难以调试,建议拆分成多步操作。
何时使用
einsum ?- 需要简洁表达复杂张量运算时(如高维缩并)。
- 需要显式控制计算流程时(避免隐式广播或转置)。
总结公式
若输入张量维度为:
- 张量1:
(d1, d2, ..., dn) - 张量2:
(e1, e2, ..., em)
表达式规则:
- 输入维度标记中重复的字母会被求和。
- 输出维度由箭头后的字母顺序决定。
例如:
-
"ijk,jl->ikl" 表示对第2个维度j 求和,输出维度为i,k,l。
-


评论记录:
回复评论: