FBI WARNING：鄙人首个开源电子书 《Go 编码建议》已经上线啦，欢迎各位大佬斧正指导，协同共建。

1.浮点数的存储格式

浮点数（Floating-point Number）是对实数的一种近似表示，由一个有效数字（即尾数）加上幂数来表示，通常是乘以某个基数的整数次幂得到。以这种表示法表示的数值，称为浮点数。表示方法类似于基数为 10 的科学计数法。利用浮点进行运算，称为浮点计算，这种运算通常伴随着因为无法精确表示而进行近似或舍入。

计算机对浮点数的表示规范遵循电气和电子工程师协会（IEEE）推出的 IEEE754 标准，浮点数在 C/C++ 中对应 float 和 double 类型，我们有必要知道浮点数在计算机中实际存储的内容。

IEEE754 标准中规定 float 单精度浮点数在机器中表示用 1 位表示数字的符号，用 8 位表示指数，用 23 位表示尾数，即小数部分。对于 double 双精度浮点数，用 1 位表示符号，用 11 位表示指数，52 位表示尾数，其中指数域称为阶码。IEEE754 浮点数的格式如下图所示。

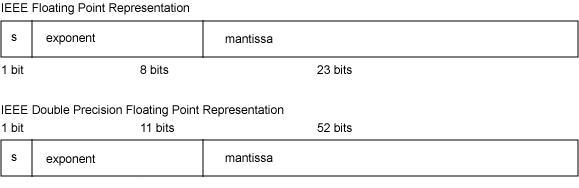
注意，IEE754 规定浮点数阶码 E 采用"指数ｅ的移码-1"来表示，请记住这一点。为什么指数移码要减去 1，这是 IEEE754 对阶码的特殊要求，以满足特殊情况，比如对正无穷的表示。

2.移码

移码（又叫增码）是对真值补码的符号位取反，一般用作浮点数的阶码，引入的目的是便于浮点数运算时的对阶操作。

对于定点整数，计算机一般采用补码的来存储。正整数的符号位为 0，反码和补码等同于原码。负整数符号位为1，原码、反码和补码的表示都不相同，由原码变成反码和补码有如下规则：
（1）原码符号位为1不变，整数的每一位二进制数位求反得反码；
（2）反码符号位为1不变，反码数值位最低位加1得补码。

比如，以一个字节 8bits 来表示 -3，那么$[-3{]}_{原}=10000011$，$[-3{]}_{反}=11111100$，$[-3{]}_{补}=11111101$，那么 -3 的移码就是$[-3{]}_{移}=01111101$。

如何将移码转换为真值 -3 呢？先将移码转换为补码，再求值。

3.浮点数的规格化

若不对浮点数的表示作出明确规定，同一个浮点数的表示就不是唯一的。例如$(1.75{)}_{10}$可以表示成 $1.11\times 2^0$，$0.111\times 2^1$，$0.0111\times 2^2$ 等多种形式。当尾数不为 0 时，尾数域的最高有效位为1，这称为浮点数的规格化。否则，以修改阶码同时左右移动小数点位置的办法，使其成为规格化数的形式。

3.1 单精度浮点数真值

IEEE754 标准中，一个规格化的 32 位浮点数 x 的真值表示为：
$$x=(-1{)}^S\times (1.M)\times 2^e$$
$$e=E-127$$
其中尾数域值是 1.M。因为规格化的浮点数的尾数域最左位总是 1，故这一位不予存储，而认为隐藏在小数点的左边。

在计算指数 e 时，对阶码E的计算采用原码的计算方式，因此 32 位浮点数的 8bits 的阶码 E 的取值范围是 0 到 255。其中当E为全 0 或者全 1 时，是 IEEE754 规定的特殊情况，下文会另外说明。

3.2 双精度浮点数真值

64 位的浮点数中符号为 1 位，阶码域为 11 位，尾数域为 52 位，指数偏移值是 1023。因此规格化的 64 位浮点数 x 的真值是：
$$x=(-1{)}^S\times (1.M)\times 2^e$$
$$e=E-1023$$

4.浮点数的具体表示

4.1 十进制到机器码

（1）0.5
$0.5=(0.1{)}_2$，符号位S为0，指数为$e=-1$，规格化后尾数为1.0。

单精度浮点数尾数域共23位，右侧以0补全，尾数域：
$$M=[00000000000000000000000{]}_2$$

阶码E:
$$E=[-1{]}_{移}-1=[01111111{]}_2-1=[01111110{]}_2$$

对照单精度浮点数的存储格式，将符号位S，阶码E和尾数域M存放到指定位置，得0.5的机器码：
$$0.5=[00111111000000000000000000000000{]}_2$$。

十六进制表示为0.5=0x3f000000。

（2）1.5
$1.5=[1.1{]}_2$，符号位为0，指数$e=0$，规格化后尾数为1.1。

尾数域Ｍ右侧以0补全，得尾数域:
$$M=[10000000000000000000000{]}_2$$

阶码E：
$$E=[\mathrm{０}{]}_{移}-1=[10000000{]}_2-1=[01111111{]}_2$$

得1.5的机器码：
$$1.5=[00111111110000000000000000000000{]}_2$$

十六进制表示为1.5=0x3fc00000。

（3）-12.5
$-12.5=[-1100.1{]}_2$，符号位S为1，指数e为3，规格化后尾数为1.1001，

尾数域Ｍ右侧以0补全，得尾数域:
$$M=[10010000000000000000000{]}_2$$

阶码E：
$$E=[3{]}_{移}-1=[10000011{]}_2-1=[10000010{]}_2$$

即-12.5的机器码：
$$-12.5=[11000001010010000000000000000000{]}_2$$

十六进制表示为-12.5=0xc1480000。

用如下程序验证上面的推算，代码编译运行平台 Win32+VC++ 2012：

#include 
using namespace std;

int main() {
	float a=0.5;
	float b=1.5;
	float c=-12.5;

	unsigned int* pa=NULL;
	pa=(unsigned int*)&a;
	unsigned int* pb=NULL;
	pb=(unsigned int*)&b;
	unsigned int* pc=NULL;
	pc=(unsigned int*)&c;
	
	cout<<hex<<"a=0x"<<*pa<<endl;
	cout<<hex<<"b=0x"<<*pb<<endl;
	cout<<hex<<"c=0x"<<*pc<<endl;
	
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

输出结果：

a=0x3f000000
b=0x3fc00000
c=0xc1480000
1
2
3

验证正确。

4.2 机器码到十进制

（1）若浮点数 x 的 IEEE754 标准存储格式为 0x41360000，那么其浮点数的十进制数值的推演过程如下：

$$0x41360000=[01000001001101100000000000000000]$$

根据该浮点数的机器码得到符号位 S=0，指数 e=阶码-127=1000 0010-127=130-127=3。

注意，根据阶码求指数时，可以像上面直接通过 "阶码-127"求得指数e，也可以将$阶码+1=移码$，再通过移码求其真值便是指数 e。比如上面阶码 $10000010+1=10000011_{[移码]}=>00000011_{[补]}=3(指数e)$。

包括尾数域最左边的隐藏位 1，那么尾数 1.M=1.011 0110 0000 0000 0000 0000=1.011011。

于是有：
$$x=(-1{)}^S\times 1.M\times 2^e=+(1.011011)\times 2^3=+1011.011=(11.375{)}_{10}$$

通过代码同样可以验证上面的推算：

#include 
using namespace std;

int main() {
	unsigned int hex=0x41360000;
	float* fp=(float*)&hex;
	cout<<"x="<<*fp<<endl;
	return 0;
}
1
2
3
4
5
6
7
8
9

输出结果：

x=11.375
1

验证正确。

5.浮点数的几种特殊情况

（1）0 的表示

对于阶码为 0 或 255 的情况，IEEE754 标准有特别的规定：
如果 阶码 E=0 并且尾数 M 是 0，则这个数的真值为 ±0（正负号和符号位有关）。

因此 +0 的机器码为：0 00000000 000 0000 0000 0000 0000 0000。
-0 的机器码为：1 00000000 000 0000 0000 0000 0000 0000。

需要注意一点，浮点数不能精确表示 0，而是以很小的数来近似表示 0，因为浮点数的真值等于（以32bits单精度浮点数为例）：
$$x=(-1{)}^S\times (1.M)\times 2^e$$
$$e=E-127$$
那么 +0 的机器码对应的真值为$1.0\times 2^{-127}$。同理，-0 机器码真值为$-1.0\times 2^{-127}$。

（2）$+\infty$ 和 $-\infty$ 的表示

如果阶码 E=255 并且尾数 M 全是0，则这个数的真值为 ±∞（同样和符号位有关）。因此$+\infty$的机器码为：0 11111111 000 0000 0000 0000 0000 0000。$-\infty$的机器吗为：1 11111111 000 0000 0000 0000 0000 0000。

（3）NaN（Not a Number）

如果 E = 255 并且 M 不是0，则这不是一个数（NaN）。

6.浮点数的精度和数值范围

6.1 浮点数的数值范围

根据上面的探讨，浮点数可以表示-∞到+∞，这只是一种特殊情况，显然不是我们想要的数值范围。

以 32 位单精度浮点数为例，阶码 E 由 8 位表示，取值范围为 0-255，去除 0 和 255 这两种特殊情况，那么指数 e 的取值范围就是 1-127=-126 到 254-127=127。

（1）最大正数
因此单精度浮点数最大正数值的符号位S=0，阶码 E=254，指数e=254-127=127，尾数M=111 1111 1111 1111 1111 1111，其机器码为：0 11111110 111 1111 1111 1111 1111 1111。

那么最大正数值:
$$PosMax=(-1{)}^S\times 1.M\times 2^e=+(1.11111111111111111111111)\times 2^{127}\approx 3.402823e+38$$
这是一个很大的数。

（2）最小正数
最小正数符号位 S=0，阶码 E=1，指数 e=1-127=-126，尾数 M=0，其机器码为 0 00000001 000 0000 0000 0000 0000 0000。

那么最小正数为：
$$PosMin=(-1{)}^S\times 1.M\times 2^e=+(1.0)\times 2^{-126}\approx 1.175494e-38$$

这是一个相当小的数。几乎可以近似等于 0。当阶码 E=0，指数为 -127 时，IEEE754 就是这么规定$1.0\times 2^{-127}$近似为0的，事实上，它并不等于 0。

（3）最大负数
最大负数符号位S=1，阶码E=1，指数e=1-127==-126，尾数 M=0，机器码与最小正数的符号位相反，其他均相同，为：1 00000001 000 0000 0000 0000 0000 0000。

最大负数等于：
$$NegMax=(-1{)}^S\times 1.M\times 2^e=-(1.0)\times 2^{-126}\approx -1.175494e-38$$

（4）最小负数
符号位S=0，阶码E=254，指数e=254-127=127，尾数M=111 1111 1111 1111 1111 1111，其机器码为：1 11111110 111 1111 1111 1111 1111 1111。

计算得：
$$NegMin=(-1{)}^S\times 1.M\times 2^e=+(1.11111111111111111111111)\times 2^{127}=-3.402823e+38$$

6.2 浮点数的精度

说到浮点数的精度，先给精度下一个定义。浮点数的精度是指浮点数的有效数字的最大位数，从左边第一个不为 0 的数字开始的个数。

阶码的二进制位数决定浮点数的表示范围，尾数的二进制位数决定浮点数的精度。以 32 位浮点数为例，尾数域有 23 位，加上规格化后小数点前隐藏的一位 1，那么浮点数以二进制表示的话精度是 24 位，24 位所能表示的最大数是$2^{24}-1=16,777,215$，共 8 位，所以 float 最多能表示十进制有效数字 8 位，但绝对能保证的为 7 位，即 float 的十进制精度为 7~8 位。

下面代码验证一下：

#include 
#include 
using namespace std;

int main() {
	float a = 16777215; // 二进制原码 1111111 11111111 11111111 有效数字 24 位 => 机器码为 0 10010110 111111 11111111 11111111 = 0x4b7fffff
    float b = 16777215.5; // 二进制原码 1111111 11111111 11111111.1 有效数字超过 24 位，无法精确表示
    
	unsigned int *pa = NULL;
  	pa = (unsigned int *) &a;
  	unsigned int *pb = NULL;
  	pb = (unsigned int *) &b;

  	cout << hex << "a=0x" << *pa << endl;
  	cout << hex << "b=0x" << *pb << endl;

  	cout << setprecision (8) << a << endl;
  	cout << setprecision (8) << b << endl;

	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

运行输出：

a=0x4b7fffff
b=0x4b800000
16777215
16777216
1
2
3
4

因为 16777215.5 转换为二进制后，有效数字超过了 24 位，所以进行了四舍五入，变成了 16777216。

64 位双精度浮点数的尾数域 52 位，加上规格化后小数点前的 1 位 共 53 位，因 $2^{53}-1=9,007,199,254,740,991$，共 16 位，所以双精度浮点数的十进制精度最高为 16 位，绝对保证 15 位，所以 double 的十进制精度为 15~16 位。

7.小结

本文操之过急，难免出现编辑错误和不当说法，请网友批评指正。不明之处，欢迎留言交流。对浮点数的加减乘除运算还未涉及，后续可能会去学习并记录学习所得，与大家分享。

参考文献

百度百科.移码
百度知道.关于IEEE754标准浮点数阶码的移码
白中英.计算机组成原理第四版[M].科学出版社:P16-30
维基百科.浮点数
百度百科.有效位数