数据结构与算法分析（八）--- 如何实现并用好一个散列表？

文章目录

一、如何快速完成搜索

1.1 什么是索引

你可能会好奇，在谷歌或百度上搜索一个关键词，马上就能给出相关的结果，为何会这么快呢？搜索引擎怎样实现的结果查找过程呢？我们在windows系统中搜索某个关键词也没那么快啊。

要想实现在一个磁盘上查找某个文件的功能，最简单的就是顺序查找，挨个从头到尾遍历并比对一遍文件名。对比前面的几种排序算法，很显然顺序查找的效率比较低，大概是O(n)，windows系统中搜索某个关键词也正是使用了这种方式，所以看起来查找比较慢。

如果想进一步提高效率，我们可以先将所有文件按字典序排序，然后使用二分查找就能极大提高查找效率（O(logn)时间）。但二分查找需要先对数据排序，排序的代价比较高（高级排序算法也需要O(n*logn)时间），如果数据是静态的，增加、删除、修改元素比较少，先对数据排序，再使用二分查找效率还不错，我们平时查字典就是按照二分查找进行的。但网络上新增、删除、修改文件比较频繁，要时刻维持文件的有序，成本就比较高了。

搜索引擎是如何做到在很短时间内从数亿文件中找到与关键词相关的网页的呢？还记得我们阅读过的很多专业书籍后面都有索引页吗？借助索引页，可以通过某关键词迅速查找到该关键词出现的页码或页码范围，借助索引查找效率就比二分查找高多了（O(1)时间）。以《数据结构与算法分析—C语言描述》为例，分治算法出现在365-380处、归并排序出现在230-235处、快速排序出现在235-247处等。

搜索引擎也是使用了类似书籍中的索引页，比如谷歌为每个可能的搜索关键词建立索引，索引中记录了包含该关键词的网页的存储位置。我们搜索某个关键词时，根据索引可以迅速定位包含该关键词的相关网页的存储位置。假如同时搜索多个关键词，则可以将每个关键词在索引中记录的网页集合取交集，搜索引擎就可以返回同时包含多个关键词的网页。

1.2 如何在索引中迅速找到关键词

有了索引，我们不需要对网页文件进行排序，就可以使用O(1)时间快速查找到所需要的网页信息，对于不断变动的数据文件，我们只需要更新部分索引，省去了维持数据文件有序的成本开销。索引的建立和更新也比较简单，在一个数据文件创建、删除或修改时，将该数据文件中包含的所有关键词对应的索引项中新增或移除该数据文件的位置即可。但是，我们如何在索引表中快速查找到关键词条目呢？

书籍后面的索引页中，关键词是按照字典序排列的，可以使用二分查找快速找到某关键词在索引页中出现的位置。在计算机中，还有更快的查找方式吗？再回顾下索引是如何在O(1)时间内给出结果的，索引条目实际上相当于在关键词和数据文件之间建立了一个一对多的映射关系，我们在索引中找到了关键词key，就可以立即获得该关键词条目中记录的数据文件位置value。查找索引关键词是否也能借助这个映射技巧实现呢？

在计算机中，索引是存储在内存地址空间中的，我们之前了解过顺序表与链式表，顺序表能够实现O(1)时间的随机访问效率，在顺序表中我们可以将一个数组元素分为两部分：数组下标记录该数组元素在内存中的地址；数组元素值记录在该存储单元中存储的数据。通过数组下标可以在O(1)时间访问该数组元素值，相当于数组元素下标位置与数组元素值之间有一个一对一的映射关系。使用数组下标访问元素值，对计算机很方便，但对于我们并不方便（我们对数字编号不敏感，更习惯概念名称检索信息），我们更喜欢使用关键词访问对应的元素值，能否在数组下标与关键词之间建立一个一对一的映射关系呢？

在计算机中，数字、词汇、符号等都是使用二进制编码的，关键词与数组下标之间建议一对一的映射关系也是可能的。我们通过一个函数，将关键词映射为数组下标，在保存索引条目：关键字–元素值（key–value）时，通过映射函数在内存中存储为数组下标–元素值的形式；当需要使用关键字key访问其对应的元素值value时，再通过通用的映射函数，将关键词映射为索引数组中的下标，就可以使用数组O(1)时间的随机访问效率，快速查找到该索引数组下标存储的元素值value，也就间接实现了通过关键字key在O(1)时间访问其对应的元素值value的目的。
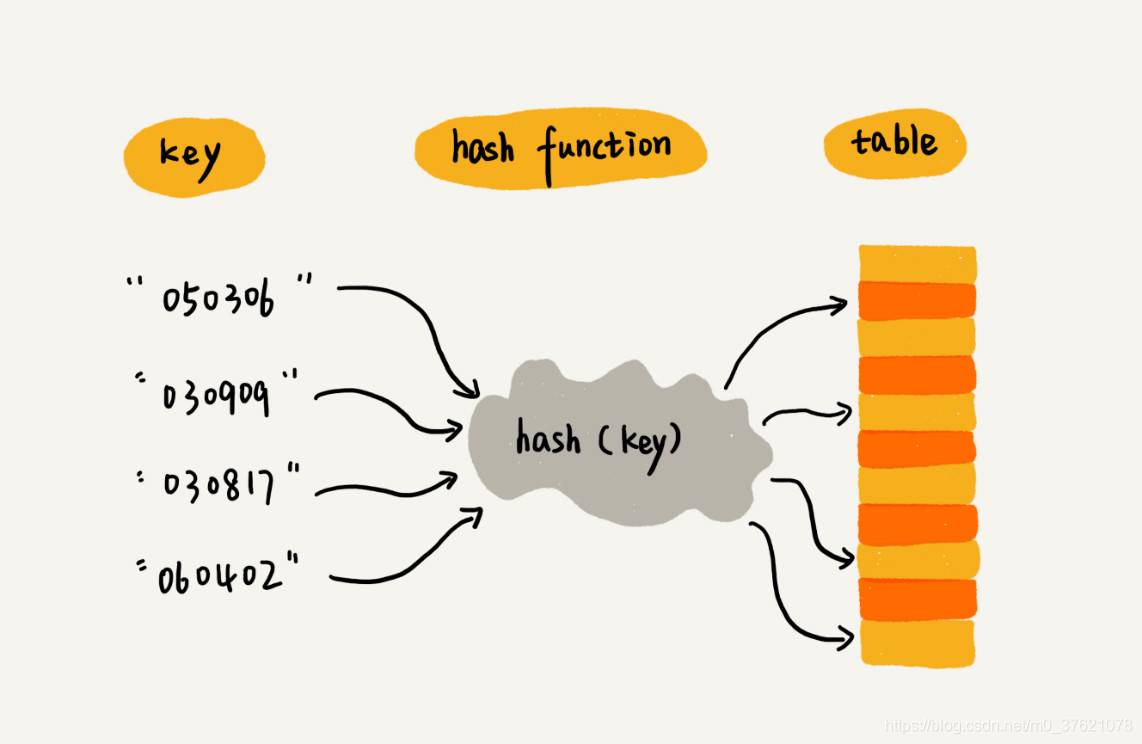
散列表逻辑结构
上面这种可以将关键词key映射为数组下标的函数称作散列（hash）函数，借助hash函数保存key–value索引条目的数组称为散列表（hash table）。散列表的插入、删除、查找或替换操作都需要两步：先通过hash函数将关键词key映射为数组下标，再通过数组下标访问关键字key对应的元素值value。

散列表的物理存储结构依然是数组，逻辑存储结构是key–value键值索引对儿，相比数组O(n)的插入与删除时间复杂度，散列表的插入、删除、访问或替换时间复杂度都是O(1)。看起来散列表集中了数组与链表的优点，既能高效的访问数据，又能高效的插入、删除数据，这是怎么做到的呢？

散列表继承了数组通过下标快速访问元素值的优点，数组插入、删除元素需要空出新位置或挤占空位置来保证数组元素间的邻接关系，散列表放弃了元素间的邻接关系，允许空位置的存在，因此可以达到链式表的元素插入、删除效率（时间复杂度O(1)）。由于散列表利用的是数组支持按照下标随机访问元素的特性，底层并不能通过链式表来实现散列表。

凡事有收益就有代价，散列表相比数组放弃了元素间的邻接关系，也没有存储类似链表的指向关系，因此散列表中的元素间没有关系，散列表并不是线性表（可以把散列表看作一个元素集合）。

二、如何实现一个散列表

2.1 什么是散列函数

散列函数在散列表中起着非常关键的作用，完成将关键字key映射为散列表元素下标的作用。我们可以把散列函数定义为hash(key)，其中key表示元素索引的关键词，hash(key)的值表示经过散列函数计算得到的散列值，也即散列表中关键词key映射到的数组下标。那么，该如何构造散列函数呢？

散列函数设计需要满足以下基本要求：

  • 散列函数计算得到的散列值是一个非负整数（数组下标非负）；
  • 如果key1 == key2，则hash(key1) == hash(key2)；
  • 如果key1 != key2，则hash(key1) != hash(key2)；

散列函数理想情况下需要实现关键词key与散列值hash(key)之间一对一的映射关系，相同的键值key具有相同的散列值hash(key)，不同的键值key具有不同的散列值hash(key)。但在真实情况下，要想找到一个不同的键值key对应的散列值都不一样的散列函数，几乎是不可能的，即便像业界著名的MD5、SHA、CRC等哈希算法，也无法完全避免这种散列冲突（即不同的键值key可能有相同的散列值）。

因为数组的存储空间有限，当元素数量接近数组容量的某个比值后，也会加大散列冲突的概率。我们几乎无法找到一个完美的无冲突的散列函数，即便能找到，付出的时间成本、计算成本也是很大的，所以针对散列冲突问题，我们需要通过其它方法来解决。

2.2 如何解决散列冲突

再好的散列函数也无法避免散列冲突。那究竟该如何解决散列冲突问题呢？我们常用的散列冲突解决方法有两类，开放寻址法（open addressing）和链表法（chaining）。

  • 开放寻址法

开放寻址法的核心思想是，如果出现了散列冲突，我们就重新探测一个空闲位置，将其插入。那如何重新探测新的位置呢？我先讲一个比较简单的探测方法，线性探测（Linear Probing）。

当我们往散列表中插入数据时，如果某个数据经过散列函数散列之后，存储位置已经被占用了，我们就从当前位置开始，依次往后查找，看是否有空闲位置，直到找到为止。举一个例子具体说明一下，下面黄色的色块表示空闲位置，橙色的色块表示已经存储了数据：
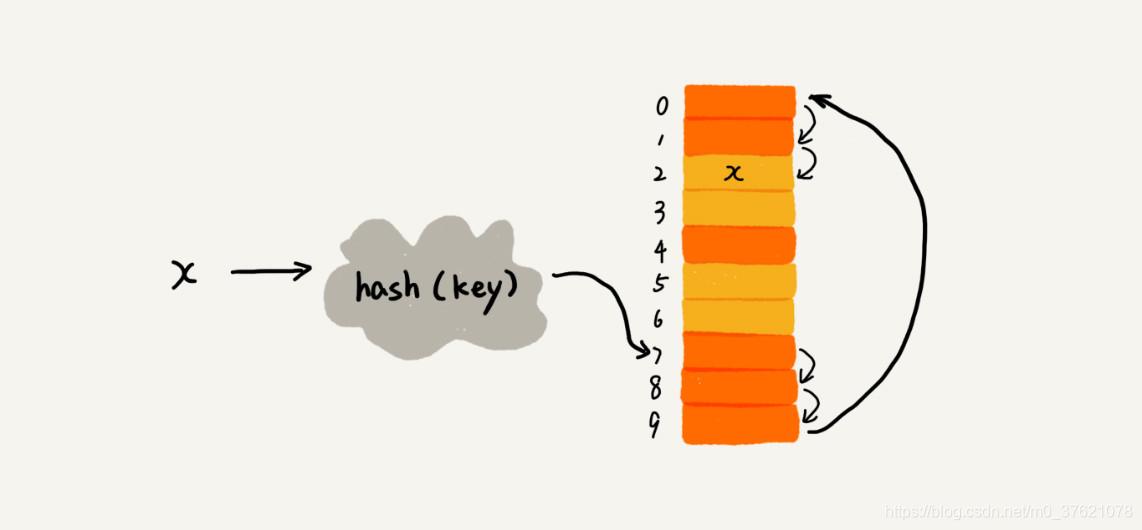
散列表线性探测示例
从图中可以看出，散列表的大小为 10，在元素 x 插入散列表之前，已经 6 个元素插入到散列表中。x 经过 Hash 算法之后，被散列到位置下标为 7 的位置，但是这个位置已经有数据了，所以就产生了冲突。于是我们就顺序地往后一个一个找，看有没有空闲的位置，遍历到尾部都没有找到空闲的位置，于是我们再从表头开始找，直到找到空闲位置 2，于是将其插入到这个位置。

在散列表中查找元素的过程有点儿类似插入过程。我们通过散列函数求出要查找元素的键值对应的散列值，然后比较数组中下标为散列值的元素和要查找的元素。如果相等，则说明就是我们要找的元素；否则就顺序往后依次查找。如果遍历到数组中的空闲位置，还没有找到，就说明要查找的元素并没有在散列表中。

散列表跟数组一样，不仅支持插入、查找操作，还支持删除操作。对于使用线性探测法解决冲突的散列表，删除操作稍微有些特别。我们不能单纯地把要删除的元素设置为空。这是为什么呢？

还记得我们刚讲的查找操作吗？在查找的时候，一旦我们通过线性探测方法，找到一个空闲位置，我们就可以认定散列表中不存在这个数据。但是，如果这个空闲位置是我们后来删除的，就会导致原来的查找算法失效。本来存在的数据，会被认定为不存在。这个问题如何解决呢？

我们可以将删除的元素，特殊标记为 deleted。当线性探测查找的时候，遇到标记为 deleted 的空间，并不是停下来，而是继续往下探测。
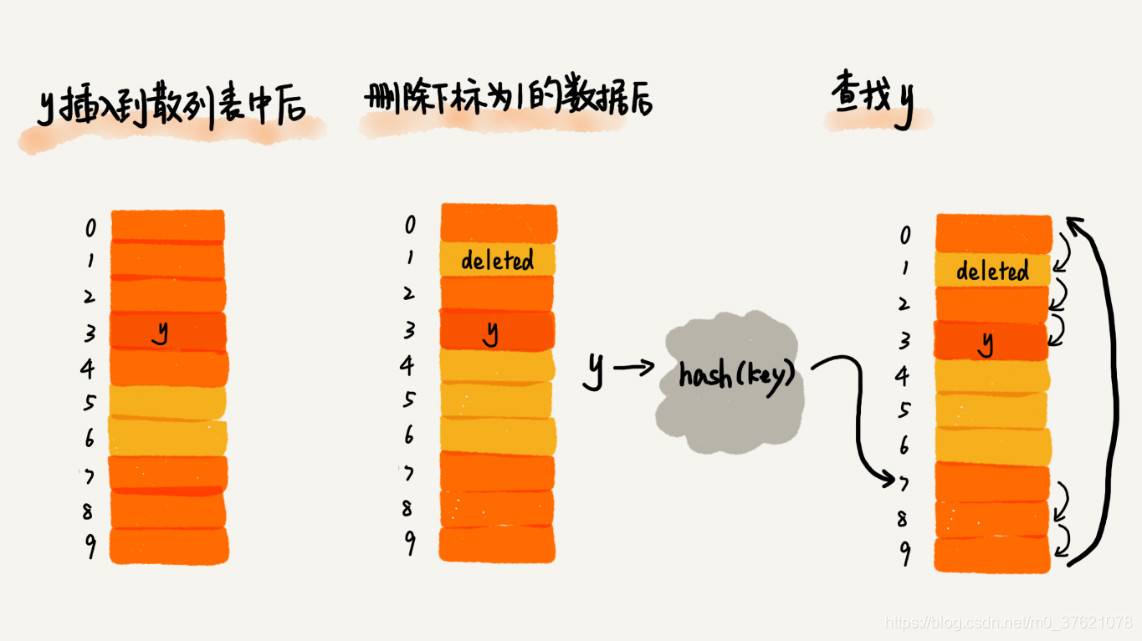
线性探测删除元素
你可能已经发现了，线性探测法其实存在很大问题。当散列表中插入的数据越来越多时，散列冲突发生的可能性就会越来越大，空闲位置会越来越少，线性探测的时间就会越来越久。极端情况下，我们可能需要探测整个散列表，所以最坏情况下的时间复杂度为 O(n)。同理，在删除和查找时，也有可能会线性探测整张散列表，才能找到要查找或者删除的数据。

对于开放寻址冲突解决方法，除了线性探测方法之外，还有另外两种比较经典的探测方法，二次探测（Quadratic probing）和双重散列（Double hashing）。

所谓二次探测，跟线性探测很像，线性探测每次探测的步长是 1，那它探测的下标序列就是 hash(key)+0，hash(key)+1，hash(key)+2……而二次探测探测的步长就变成了原来的“二次方”，也就是说，它探测的下标序列就是 hash(key)+0，hash(key)+12，hash(key)+22……

所谓双重散列，意思就是不只要使用一个散列函数。我们使用一组散列函数 hash1(key)，hash2(key)，hash3(key)……我们先用第一个散列函数，如果计算得到的存储位置已经被占用，再用第二个散列函数，依次类推，直到找到空闲的存储位置。

不管采用哪种探测方法，当散列表中空闲位置不多的时候，散列冲突的概率就会大大提高。为了尽可能保证散列表的操作效率，一般情况下，我们会尽可能保证散列表中有一定比例的空闲槽位。我们用装载因子（load factor）来表示空位的多少，装载因子的计算公式是：

散列表的装载因子 = 填入表中的元素个数 / 散列表的长度

装载因子越大，说明空闲位置越少，冲突越多，散列表的性能会下降。

  • 链表法

链表法是一种更加常用的散列冲突解决办法，相比开放寻址法，它要简单很多。在散列表中，每个“桶（bucket）”或者“槽（slot）”会对应一条链表，所有散列值相同的元素我们都放到相同槽位对应的链表中，如下图所示：
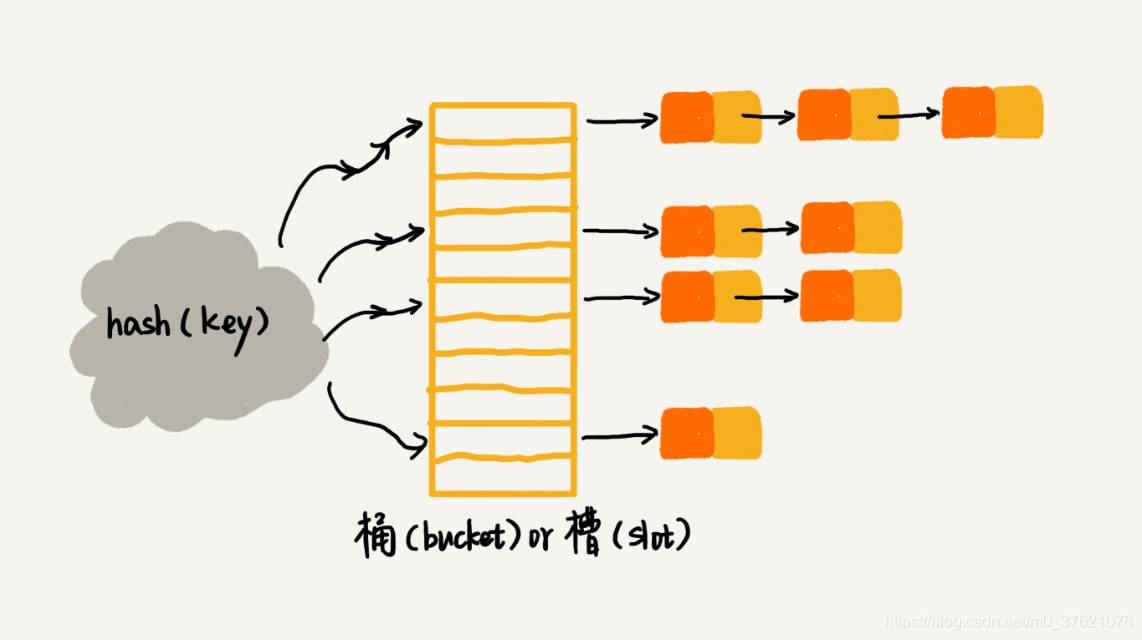
链表法图示
当插入的时候，我们只需要通过散列函数计算出对应的散列槽位，将其插入到对应链表中即可，所以插入的时间复杂度是 O(1)。当查找、删除一个元素时，我们同样通过散列函数计算出对应的槽，然后遍历链表查找或者删除。那查找或删除操作的时间复杂度是多少呢？

实际上，这两个操作的时间复杂度跟链表的长度 k 成正比，也就是 O(k)。对于散列比较均匀的散列函数来说，理论上讲，k=n/m，其中 n 表示散列中数据的个数，m 表示散列表中“槽”的个数。

2.3 如何设计散列函数

散列函数设计的好坏，决定了散列表冲突的概率大小，也直接决定了散列表的性能。那什么才是好的散列函数呢？

首先，散列函数的设计不能太复杂。过于复杂的散列函数，势必会消耗很多计算时间，也就间接的影响到散列表的性能。其次，散列函数生成的值要尽可能随机并且均匀分布，这样才能避免或者最小化散列冲突，而且即便出现冲突，散列到每个槽里的数据也会比较平均，不会出现某个槽内数据特别多的情况。

实际工作中，我们还需要综合考虑各种因素。这些因素有关键字的长度、特点、分布、还有散列表的大小等。散列函数各式各样，我举几个常用的、简单的散列函数的设计方法，让你有个直观的感受。

第一个例子，比如处理手机号码，因为手机号码前几位重复的可能性很大，但是后面几位就比较随机，我们可以取手机号的后四位作为散列值。这种散列函数的设计方法，我们一般叫作“数据分析法”。

第二个例子，如何实现 Word 拼写检查功能。这里面的散列函数，我们就可以这样设计：将单词中每个字母的ASCll 码值“进位”相加，然后再跟散列表的大小求余、取模，作为散列值。散列函数代码如下：

typedef unsigned int Index;

Index Hash(const char *key, int TableSize)
{
	unsigned int HashVal = 0;
	while(*key != '\0')
	{
		HashVal = HashVal * 26 + *key;
		key++;
	}
	return HashVal % TableSize;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12

上面的散列函数并没有采用直接将字符串中字符的ASCII码值相加的方法，主要是ASCII码值相加的范围较小，比如假设每个单词平均长度为8个字符长度，相加得到的散列值最大也才127 * 8 = 1016，远小于常用单词数目（假设TableSize为20000），这就会导致散列值集中在头部，分布很不均匀。因此采用了上面将单词中每个字母的ASCll 码值“进位”相加的方法，由于共有26个字母，故按26进制进位相加。如果想进一步提高计算效率，可以使用移位运算替代乘除运算，乘以26可以更改为左移5位。

实际上，散列函数的设计方法还有很多，比如直接寻址法、平方取中法、折叠法、随机数法等，这里就不再展开介绍了。重点就是前面介绍的散列函数设计原则：散列函数计算成本尽量比较低，散列函数生成的值要尽可能随机并且均匀分布。

2.4 如何进行动态扩容

前面说过，装载因子越大，说明散列表中的元素越多，空闲位置越少，散列冲突的概率就越大。不仅插入数据的过程要多次寻址或者拉很长的链，查找的过程也会因此变得很慢。

对于没有频繁插入和删除的静态数据集合来说，我们很容易根据数据的特点、分布等，设计出完美的、极少冲突的散列函数，因为毕竟之前数据都是已知的。

对于动态散列表来说，数据集合是频繁变动的，我们事先无法预估将要加入的数据个数，所以我们也无法事先申请一个足够大的散列表。随着数据慢慢加入，装载因子就会慢慢变大。当装载因子大到一定程度之后，散列冲突就会变得不可接受。这个时候，我们该如何处理呢？

还记得前面多次介绍的“动态扩容”吗？可以回想下，C++ STL Vector和Deque容器是如何做到动态扩容的。

针对散列表，当装载因子过大时，我们也可以进行动态扩容，重新申请一个更大的散列表，将数据搬移到这个新散列表中。假设每次扩容我们都申请一个原来散列表大小两倍的空间。如果原来散列表的装载因子是 0.8，那经过扩容之后，新散列表的装载因子就下降为原来的一半，变成了 0.4。

针对数组的扩容，数据搬移操作比较简单。但是，针对散列表的扩容，数据搬移操作要复杂很多。因为散列表的大小变了，数据的存储位置也变了，所以我们需要通过散列函数重新计算每个数据的存储位置。比如下图示例，在原来的散列表中，21 这个元素原来存储在下标为 0 的位置，搬移到新的散列表中，存储在下标为 7 的位置：
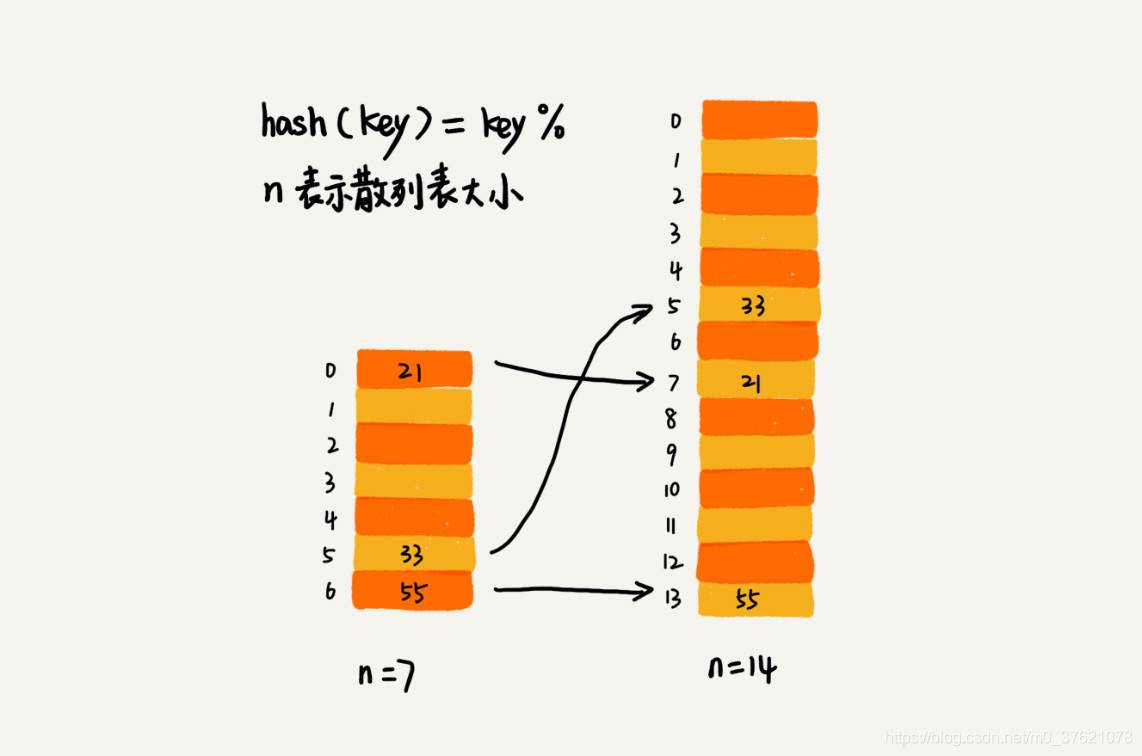
散列表扩容重散列
对于支持动态扩容的散列表，插入一个数据，最好情况下，不需要扩容，最好时间复杂度是 O(1)。最坏情况下，散列表装载因子过高，启动扩容，我们需要重新申请内存空间，重新计算哈希位置，并且搬移数据，所以时间复杂度是 O(n)。用摊还分析法，均摊情况下，时间复杂度接近最好情况，就是 O(1)。

实际上，对于动态散列表，随着数据的删除，散列表中的数据会越来越少，空闲空间会越来越多。如果我们对空间消耗非常敏感，我们可以在装载因子小于某个值之后，启动动态缩容。当然，如果我们更加在意执行效率，能够容忍多消耗一点内存空间，那就可以不用费劲来缩容了。

当散列表的装载因子超过某个阈值时，就需要进行扩容。装载因子阈值需要选择得当。如果太大，会导致冲突过多；如果太小，会导致内存浪费严重。装载因子阈值的设置要权衡时间、空间复杂度。如果内存空间不紧张，对执行效率要求很高，可以降低负载因子的阈值；相反，如果内存空间紧张，对执行效率要求又不高，可以增加负载因子的值，甚至可以大于 1。

大部分情况下，动态扩容的散列表插入一个数据都很快，但是在特殊情况下，当装载因子已经到达阈值，需要先进行扩容，再插入数据。这个时候，插入数据就会变得很慢，甚至会无法接受。

为了解决一次性扩容耗时过多的情况，我们可以将扩容操作穿插在插入操作的过程中，分批完成。当装载因子触达阈值之后，我们只申请新空间，但并不将老的数据搬移到新散列表中。当有新数据要插入时，我们将新数据插入新散列表中，并且从老的散列表中拿出一个数据放入到新散列表。每次插入一个数据到散列表，我们都重复上面的过程。经过多次插入操作之后，老的散列表中的数据就一点一点全部搬移到新散列表中了。这样没有了集中的一次性数据搬移，插入操作就都变得很快了。对于查询操作，为了兼容了新、老散列表中的数据，我们先从新散列表中查找，如果没有找到，再去老的散列表中查找。

通过这样均摊的方法，将一次性扩容的代价，均摊到多次插入操作中，就避免了一次性扩容耗时过多的情况。这种实现方式，任何情况下，插入一个数据的时间复杂度都是 O(1)。

2.5 如何选择散列冲突解决方法

前面介绍了两种主要的散列冲突的解决办法，开放寻址法和链表法。这两种冲突解决办法在实际的软件开发中都非常常用。比如，Java 中 LinkedHashMap 就采用了链表法解决冲突，ThreadLocalMap 是通过线性探测的开放寻址法来解决冲突。那你知道，这两种冲突解决方法各有什么优势和劣势，又各自适用哪些场景吗？

  • 开放寻址法

开放寻址法的优点：开放寻址法不像链表法，需要拉很多链表。散列表中的数据都存储在数组中，可以有效地利用 CPU 缓存加快查询速度。而且，这种方法实现的散列表，序列化起来比较简单。链表法包含指针，序列化起来就没那么容易。

开放寻址法的缺点：用开放寻址法解决冲突的散列表，删除数据的时候比较麻烦，需要特殊标记已经删除掉的数据。而且，在开放寻址法中，所有的数据都存储在一个数组中，比起链表法来说，冲突的代价更高。所以，使用开放寻址法解决冲突的散列表，装载因子的上限不能太大。这也导致这种方法比链表法更浪费内存空间。

总结一下，当数据量比较小、装载因子小的时候，适合采用开放寻址法。这也是 Java 中的ThreadLocalMap使用开放寻址法解决散列冲突的原因。

  • 链表法

首先，链表法对内存的利用率比开放寻址法要高。因为链表结点可以在需要的时候再创建，并不需要像开放寻址法那样事先申请好。实际上，这一点也是我们前面讲过的链表优于数组的地方。

链表法比起开放寻址法，对大装载因子的容忍度更高。开放寻址法只能适用装载因子小于 1 的情况。接近 1 时，就可能会有大量的散列冲突，导致大量的探测、再散列等，性能会下降很多。但是对于链表法来说，只要散列函数的值随机均匀，即便装载因子变成 10，也就是链表的长度变长了而已，虽然查找效率有所下降，但是比起顺序查找还是快很多。

链表因为要存储指针，所以对于比较小的对象的存储，是比较消耗内存的，还有可能会让内存的消耗翻倍。而且，因为链表中的结点是零散分布在内存中的，不是连续的，所以对 CPU 缓存是不友好的，这方面对于执行效率也有一定的影响。当然，如果我们存储的是大对象，也就是说要存储的对象的大小远远大于一个指针的大小（4 个字节或者 8 个字节），那链表中指针的内存消耗在大对象面前就可以忽略了。

实际上，我们对链表法稍加改造，可以实现一个更加高效的散列表。那就是，我们将链表法中的链表改造为其他高效的动态数据结构，比如跳表、红黑树。这样，即便出现散列冲突，极端情况下，所有的数据都散列到同一个桶内，那最终退化成的散列表的查找时间也只不过是 O(logn)。这样也就有效避免了前面讲到的散列碰撞攻击。
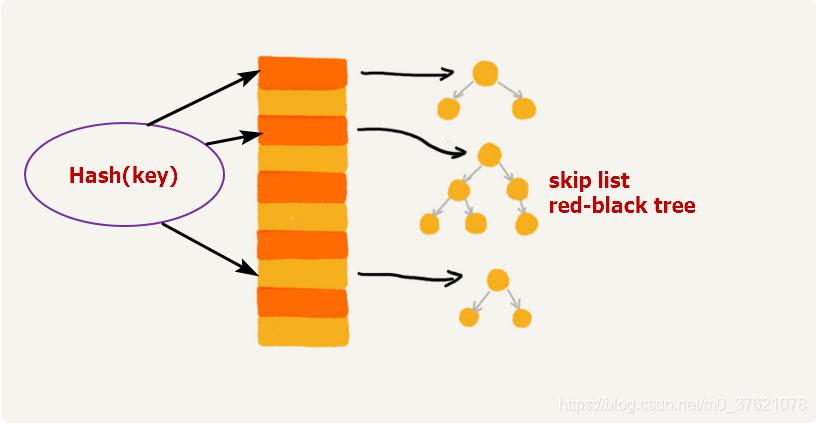
高级散列表
总结一下，基于链表的散列冲突处理方法比较适合存储大对象、大数据量的散列表，而且，比起开放寻址法，它更加灵活，支持更多的优化策略，比如用跳表或红黑树代替链表。

2.6 如何实现一个散列表

根据前面介绍的散列表知识，我们可以从三个方面来考虑设计思路：

  • 设计一个合适的散列函数；
  • 定义装载因子阈值，并且设计动态扩容策略；
  • 选择合适的散列冲突解决方法。

散列函数前面已经实现了一个，这里对其稍加改进，代码如下：

// datastruct\hash_table.c

typedef unsigned int Index;

Index Hash(const char *key, int TableSize)
{
	unsigned int HashVal = 0;
	while(*key != '\0')
	{
		HashVal = (HashVal << 5) + *key;
		key++;
	}
	return HashVal % TableSize;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14

像文章开头谈到的搜索引擎，关键词索引的数据规模比较大，我们采用链表法作为散列冲突解决方案。先看散列表的数据结构定义（包括散列表头，链表头，链表元素结点的定义）：

// datastruct\hash_table.c

struct ListNode {
    struct ListNode *next;		//指向下一个元素的地址
    KeyType key;                //当前元素结点索引关键词
    ElementType Element;	    //可以是数据集合或其它的数据结构
};
typedef struct ListNode *pNode;

struct ListHead {
    struct ListNode *next;      //指向当前链表首结点地址
    int size;                   //当前链表元素节点数量
};
typedef struct ListHead *List;

struct HashTbl
{
    int TableSize;          //散列表容量
    List *HashLists;        //散列表数组基地址指针，指向各链表头地址
    int NodeCount;          //散列表当前元素节点数量
};
typedef struct HashTbl *HashTable;

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22

给出散列表的创建，查找，插入，删除操作函数实现代码：

// datastruct\hash_table.c

HashTable HashInit(int TableSize)
{
    HashTable H;
    int i;
    // allocate hash table
    H = malloc(sizeof(struct HashTbl));
    if(H == NULL){
        printf("Out of space!");
        return NULL;
    }

    H->TableSize = TableSize;
    H->NodeCount = 0;
    // allocate array of lists
    H->HashLists = malloc((H->TableSize) * sizeof(List));
    if(H->HashLists == NULL){
        printf("Out of space!");
        return NULL;
    }
    // allocate list headers
    for(i = 0; i < H->TableSize; i++)
    {
        H->HashLists[i] = malloc(sizeof(struct ListHead));
        if(H->HashLists[i] == NULL){
            printf("Out of space!");
            return NULL;
        }

        H->HashLists[i]->size = 0;
        H->HashLists[i]->next = NULL;
    }
    return H;
}

pNode HashFind(HashTable H, KeyType key)
{
    List L = H->HashLists[Hash(key, H->TableSize)];
    pNode P = L->next;

    while (P != NULL && P->key != key)
        P = P->next;
    
    return P;
}

void HashInsert(HashTable H, KeyType key, ElementType data)
{
    pNode pos = HashFind(H, key);
    if(pos == NULL)
    {  
        pNode P = malloc(sizeof(struct ListNode));
        if(P == NULL){
            printf("Out of space!");
            return;
        }

        List L = H->HashLists[Hash(key, H->TableSize)];

        P->key = key;
        P->Element = data;
        P->next = L->next;
        L->next = P;

        L->size++;
        H->NodeCount++;
    }
}

void HashDelete(HashTable H, KeyType key)
{
    List L = H->HashLists[Hash(key, H->TableSize)];
    pNode prev = (pNode)L;
    while (prev->next != NULL && prev->next->key != key)
        prev = prev->next;
    
    if(prev->next != NULL)
    {
        List L = H->HashLists[Hash(key, H->TableSize)];
        pNode temp = prev->next;
        prev->next = temp->next;
        free(temp);
        
        L->size--;
        H->NodeCount--;
    }
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59
  • 60
  • 61
  • 62
  • 63
  • 64
  • 65
  • 66
  • 67
  • 68
  • 69
  • 70
  • 71
  • 72
  • 73
  • 74
  • 75
  • 76
  • 77
  • 78
  • 79
  • 80
  • 81
  • 82
  • 83
  • 84
  • 85
  • 86
  • 87
  • 88

链表法对散列冲突的容忍性较强，装载因子可以略大些，比如超过3，开放寻址法对散列冲突的容忍性较差，装载因子建议不超过0.5。上面选择链表法作为散列冲突解决方案，为方便示例，装载因子暂设为1。

散列表的动态扩容函数实现代码如下：

// datastruct\hash_table.c

HashTable ReHashDouble(HashTable H)
{
    HashTable OldHash = H;

    H = HashInit(2 * (OldHash->TableSize));

    int i;
    for(i = 0; i < OldHash->TableSize; i++)
    {
        List L = OldHash->HashLists[i];
        pNode P = L->next;
        while (P != NULL)
        {
            HashInsert(H, P->key, P->Element);
            pNode temp = P;
            P = P->next;
            free(temp);
        }
        free(L);
    }
    free(OldHash->HashLists);
    free(OldHash);

    return H;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27

到这里就实现了一个支持动态扩容的散列表，下面给出一个应用示例，验证一下我们实现的操作函数是否有明显bug，示例代码如下：

// datastruct\hash_table.c

#include 
#include 

#define ElementType int
typedef char *KeyType;
typedef unsigned int Index;

typedef struct ListNode *pNode;
typedef struct ListHead *List;
typedef struct HashTbl *HashTable;

HashTable HashInit(int TableSize);
Index Hash(const char *key, int TableSize);
pNode HashFind(HashTable H, KeyType key);
void HashInsert(HashTable H, KeyType key, ElementType data);
void HashDelete(HashTable H, KeyType key);
HashTable ReHashDouble(HashTable H);

void PrintHash(HashTable H)
{
    int i;
    printf("Hash table size: %d, base address: %X\n", H->TableSize, H->HashLists);
    for(i = 0; i < H->TableSize; i++)
    {
        List L = H->HashLists[i];
        pNode P = L->next;
        printf("HashTable[%d]: ", i);
        while (P != NULL)
        {
            if(P != L->next)
                printf("-->");
            printf("%d", P->Element);
            P = P->next;
        }
        printf("\n");
    }
}

int main(void)
{
    HashTable H = HashInit(3);
    
    HashInsert(H, "key1", 1);
    HashInsert(H, "key2", 2);
    HashInsert(H, "key3", 3);
    HashInsert(H, "key4", 4);
    HashInsert(H, "key5", 5);
    HashInsert(H, "key6", 6);
    PrintHash(H);

    if(H->NodeCount > H->TableSize)
        H = ReHashDouble(H);
    PrintHash(H);

    KeyType key = "key3";
    pNode ptr = HashFind(H, key);
    if(ptr != NULL)
        printf("find %s data: %d\n", key, ptr->Element);

    HashDelete(H, "key1");
    HashDelete(H, "key5");
    PrintHash(H);

    return 0;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59
  • 60
  • 61
  • 62
  • 63
  • 64
  • 65
  • 66
  • 67

上面的散列表示例程序运行结果如下：
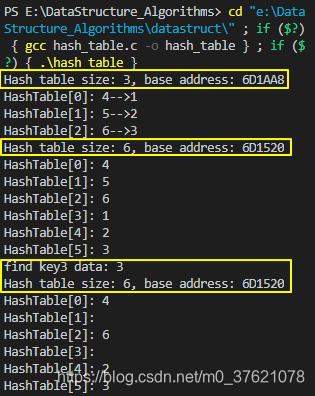
散列表示例程序运行结果

三、散列表与链表的组合应用

前面介绍过，散列表这种数据结构虽然支持非常高效的数据插入、删除、查找操作，但是散列表中的数据都是通过散列函数打乱之后无规律存储的。也就说，它无法支持按照某种顺序快速地遍历数据。如果希望按照顺序遍历散列表中的数据，那我们需要将散列表中的数据拷贝到数组中，然后排序，再遍历。

因为散列表是动态数据结构，不停地有数据的插入、删除，所以每当我们希望按顺序遍历散列表中的数据的时候，都需要先排序，那效率势必会很低。为了解决这个问题，我们可以将散列表和链表（或者跳表）结合在一起使用，通过散列表实现O(1)时间的数据插入、删除、查找操作，通过链表或跳表存储数据元素间的前后指向关系，就可以按照我们需要的某种顺序快速遍历散列表中的数据，充分发挥两种数据结构的优点，互相弥补自身的不足。

3.1 如何实现一个LRU 缓存淘汰算法

缓存是一种提高数据读取性能的技术，在硬件设计、软件开发中都有着非常广泛的应用，比如常见的 CPU 缓存、数据库缓存、浏览器缓存等等。缓存的大小有限，当缓存被用满时，哪些数据应该被清理出去，哪些数据应该被保留？这就需要缓存淘汰策略来决定。常见的策略有三种：先进先出策略 FIFO（First In，First Out）、最少使用策略 LFU（Least Frequently Used）、最近最少使用策略 LRU（Least Recently Used）。

如果我们想实现一个 LRU 缓存淘汰算法，该怎么做呢？先考虑使用链表如何实现？我们需要维护一个按照访问时间从早到晚有序排列的链表结构，越靠近链表头部的结点是越早之前访问的。因为缓存大小有限，当缓存空间不够，需要淘汰一个数据的时候，我们就直接将链表头部的结点删除。

当要缓存某个数据的时候，先在链表中查找这个数据。如果没有找到，则直接将数据放到链表的尾部；如果找到了，我们就把它移动到链表的尾部。因为查找数据需要遍历链表，所以单纯用链表实现的 LRU 缓存淘汰算法的时间复杂很高，是 O(n)。

总结一下，一个缓存（cache）系统主要包含下面这几个操作：

  • 往缓存中添加一个数据；
  • 从缓存中删除一个数据；
  • 在缓存中查找一个数据。

这三个操作都要涉及“查找”操作，如果单纯地采用链表的话，时间复杂度只能是 O(n)。如果我们将散列表和链表两种数据结构组合使用，可以将这三个操作的时间复杂度都降低到 O(1)。具体的结构就是下面这个样子：
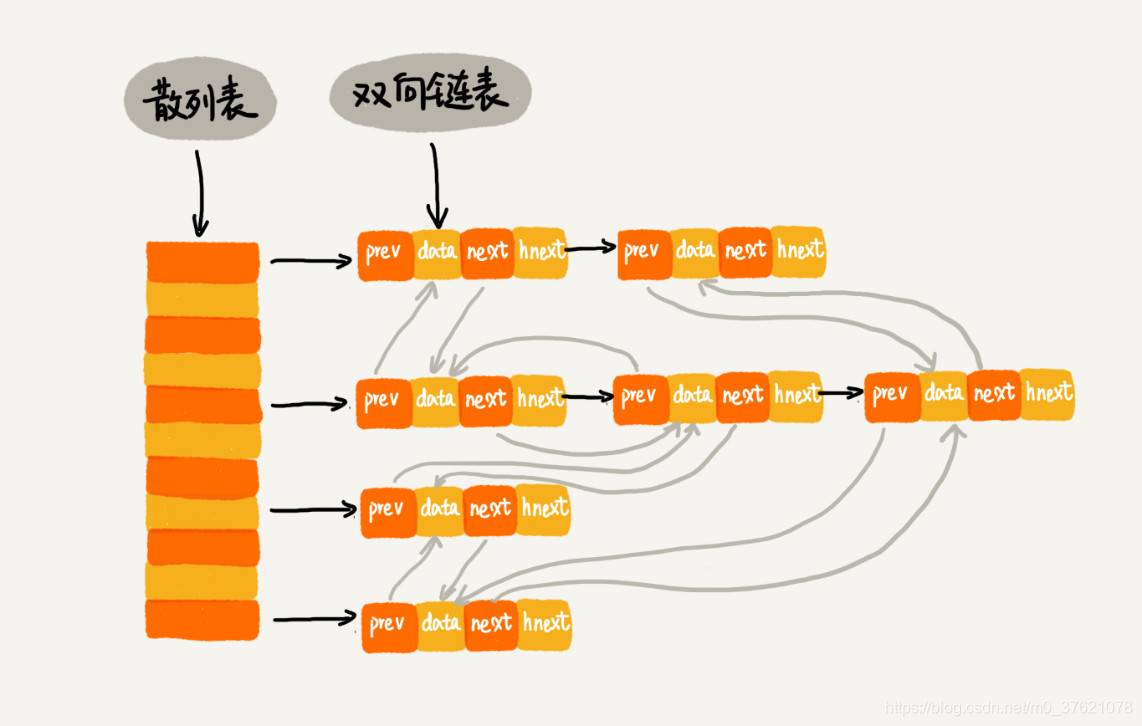
散列表与双向链表结合应用之LRU缓存淘汰算法
我们使用双向链表存储数据，链表中的每个结点处理存储数据（data）、前驱指针（prev）、后继指针（next）之外，还新增了一个特殊的字段 hnext。这个 hnext 有什么作用呢？

因为我们的散列表是通过链表法解决散列冲突的，所以每个结点会在两条链中。一个链是刚刚我们提到的双向链表，另一个链是散列表中的拉链。前驱和后继指针是为了将结点串在双向链表中，hnext 指针是为了将结点串在散列表的拉链中。

了解了这个散列表和双向链表的组合存储结构之后，我们再来看，前面讲到的缓存的三个操作，是如何做到时间复杂度是 O(1) 的？

首先，我们来看如何查找一个数据。我们前面讲过，散列表中查找数据的时间复杂度接近 O(1)，所以通过散列表，我们可以很快地在缓存中找到一个数据。当找到数据之后，我们还需要将它移动到双向链表的尾部。

其次，我们来看如何删除一个数据。我们需要找到数据所在的结点，然后将结点删除。借助散列表，我们可以在 O(1) 时间复杂度里找到要删除的结点。因为我们的链表是双向链表，双向链表可以通过前驱指针 O(1) 时间复杂度获取前驱结点，所以在双向链表中，删除结点只需要 O(1) 的时间复杂度。

最后，我们来看如何添加一个数据。添加数据到缓存稍微有点麻烦，我们需要先看这个数据是否已经在缓存中。如果已经在其中，需要将其移动到双向链表的尾部；如果不在其中，还要看缓存有没有满。如果满了，则将双向链表头部的结点删除，然后再将数据放到链表的尾部；如果没有满，就直接将数据放到链表的尾部。

这整个过程涉及的查找操作都可以通过散列表来完成。其他的操作，比如删除头结点、链表尾部插入数据等，都可以在 O(1) 的时间复杂度内完成。所以，这三个操作的时间复杂度都是 O(1)。至此，我们就通过散列表和双向链表的组合使用，实现了一个高效的、支持 LRU 缓存淘汰算法的缓存系统原型。

3.2 Redis有序集合是如何实现的

Redis（全称：Remote Dictionary Server 远程字典服务）是一个开源的使用ANSI C语言编写、支持网络、可基于内存亦可持久化的日志型、Key-Value数据库，并提供多种语言的API。它通常被称为数据结构服务器，因为值（value）可以是 字符串(String)、哈希(Hash)、列表(list)、集合(sets) 和 有序集合(sorted sets)等类型。

在Redis有序集合中，每个成员对象有两个重要的属性：key（键值）和 score（分值）。我们不仅会通过 score 来查找数据，还会通过 key 来查找数据。举个例子，比如用户积分排行榜有这样一个功能：我们可以通过用户的 ID 来查找积分信息，也可以通过积分区间来查找用户 ID 或者姓名信息。这里包含 ID、姓名和积分的用户信息，就是成员对象，用户 ID 就是 key，积分就是 score。

如果我们细化一下 Redis 有序集合的操作，那就是下面这样：

  • 添加一个成员对象；
  • 按照键值来删除一个成员对象；
  • 按照键值来查找一个成员对象；
  • 按照分值区间查找数据，比如查找积分在 [100, 356] 之间的成员对象；
  • 按照分值从小到大排序成员变量；

前面三种操作使用散列表就可以实现，而且时间复杂度为O(1)，但后两个操作散列表就无能为力了。我们该用什么数据结构来保存成员对象按照分值从小到大的排序信息呢？由于Redis是动态的，需要频繁插入、删除和查找，我们首先会想到链表，但链表的查找时间复杂度为O(n)，效率太低，还有更高效的方法吗？

还记得前面介绍过的跳表吗？跳表很适合在有序链表中实现二分查找的高效率，时间复杂度为O(logn)。而且在跳表中也很适合按照分值区间查找数据，使用O(logn)时间找到分值区间的起始分值，然后从起始分值处按顺序往后遍历跳表，直到遍历到分值区间的末尾分值即可。

Redis每个成员对象的两个属性：key（键值）和 score（分值），键值key属性使用散列表组织起来，分值score属性使用跳表组织起来，能充分发挥散列表与跳表的优势，同时互相弥补自身的不足。

本章数据结构实现源码下载地址：https://github.com/StreamAI/ADT-and-Algorithm-in-C/tree/master/datastruct

更多文章：

注：本文转载自blog.csdn.net的流云IoT的文章"https://blog.csdn.net/m0_37621078/article/details/103724492"。版权归原作者所有，此博客不拥有其著作权，亦不承担相应法律责任。如有侵权，请联系我们删除。
复制链接
相关推荐
发表评论

评论记录：

未查询到任何数据！