树状数组（Binary Indexed Tree, BIT）

• 本质上是按照二分对数组进行分组，维护和查询都是O(lgn)的复杂度

• 树状数组与线段树：树状数组和线段树很像，但能用树状数组解决的问题，基本上都能用线段树解决，而线段树能解决的树状数组不一定能解决。相比较而言，树状数组效率要高很多。

• lowbit

  • lowbit = x & (-x)
  • lowbit(x)也可以理解为能整除x的最大的2的幂次

• c[i]存放的是在i号之前（包括i号）lowbit(i)个整数的和（即：c[i]的覆盖长度是lowbit(i) ）

• 树状数组的下标必须从1开始
  

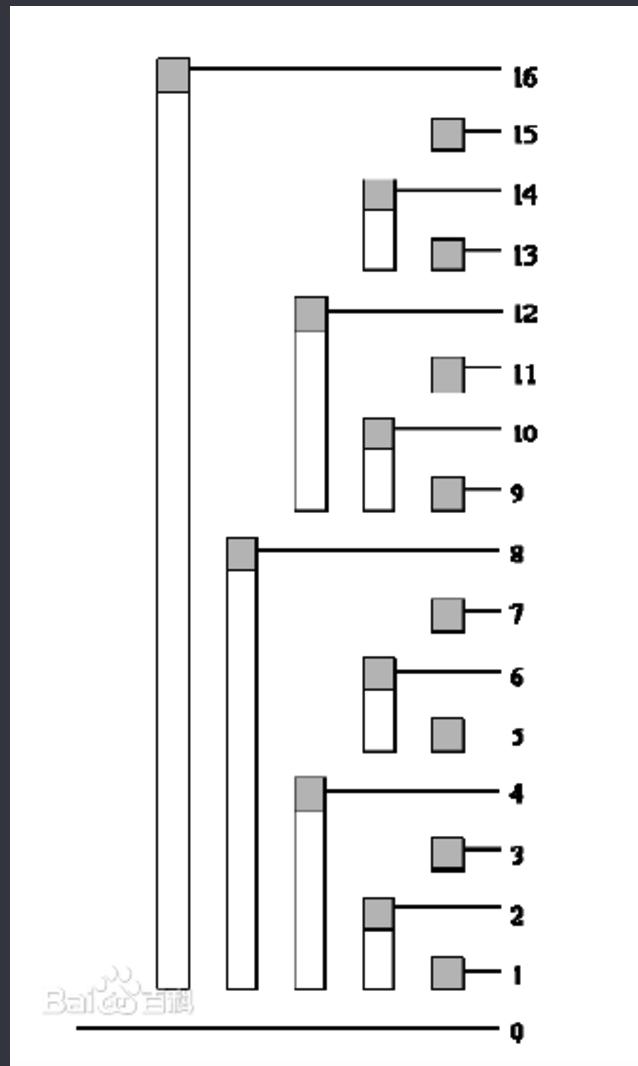
单点更新，区间查询

int getsum(int x)函数：返回前x个整数之和

int getsum(int x) {
  int sum = 0;
  for(int i = x; i >= 1; i -= lowbit(x))
    sum += c[i];
  return sum;
}
1
2
3
4
5
6

• 如果要求[x, y]之内的数的和，可以转换成getsum(y) - getsum(x - 1)来解决

void update(x, v)函数：将第x个数加上一个数v

void update(int x, int v) {
  for(int i = x; i <= n; i += lowbit(x))
    c[i] += v;
}
1
2
3
4

经典应用：统计序列中在元素左边比该元素小的元素个数

#include 
#include 
const int maxn = 10010;
#define lowbit(i) ((i) & (-i))
int c[maxn];
void update(int x, int v) {
  for(int i = x; i < maxn; i += lowbit(i))
    c[i] += v;
}
int getsum(int x) {
  int sum = 0;
  for(int i = x; i >= 1; i -= lowbit(i))
    sum += c[i];
  return sum;
}
int main() {
  int n, x;
  scanf("%d", &n);
  for(int i = 0; i < n; i++) {
    scanf("%d", &x);
    update(x, 1);
    printf("%d\n", getsum(x - 1));
  }
  return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

如果是求序列第k大的问题：

可以用二分法查询第一个满足getsum(i) >= k的i

int findKthElement(int k) {
  int l = 1, r = maxn; mid;
  while(l < r) {
    mid = (l + r) / 2;
    if(getsum(mid) >= K)
      r = mid;
    else
      l = mid + 1;
  }
  return l;
}
1
2
3
4
5
6
7
8
9
10
11

如果给定一个二维整数矩阵A，求A[1][1]~A[x][y]这个子矩阵中所有元素之和，以及给单点A[x][y]加上整数v：

只需把getsum和update函数中的for循环改为两重

int c[maxn][maxn];
void update(int x, int y, int v) {
  for(int i = x; i < maxn; i += lowbit(i)) {
    for(int j = y; j < maxn; j += lowbit(j)) {
      c[i][j] += v;
    }
  }
}

int getsum(int x, int y) {
  int sum = 0;
  for(int i = x; i >= 1; i -= lowbit(i)) {
    for(int j = y; j >= 1; j -= lowbit(j))
      sum += c[i][j];
  }
  return sum;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

区间更新，单点查询

• 将getsum改为沿着i增大lowbit(i)的方向
• 将update改为沿着i减小的lowbit(i)的方向
• c[i]不再表示这段区间的元素之和，而是表示这段区间每个数被加了多少
• int getsum(int x)返回第x个整数的值（就是从小块到大块累加一共被增加了多少）

int getsum(int x) {
  int sum = 0;
  for(int i = x; i < maxn; i += lowbit(i))
    sum += c[i];
  return sum;
}
1
2
3
4
5
6

• void update(int x, int v)是将前x个整数都加上v

void update(int x, int v) {
  for(int i = x; i >= 0; i -= lowbit(i))
    c[i] += v;
}
1
2
3
4

• 所以，~~i从x往后是从小块更新到大块c[i]，i从x往前是累加前面的覆盖块的值~

1057. Stack (30)-PAT甲级真题（树状数组）

• 求栈内所有元素的中位数：用排序查询的方法会超时~~~用树状数组，即求第k = (s.size() + 1) / 2大的数。查询小于等于x的数的个数是否等于k的时候用二分法更快~

#include 
#include 
#define lowbit(i) ((i) & (-i))
const int maxn = 100010;
using namespace std;
int c[maxn];
stack s;
void update(int x, int v) {
    for(int i = x; i < maxn; i += lowbit(i))
        c[i] += v;
}
int getsum(int x) {
    int sum = 0;
    for(int i = x; i >= 1; i -= lowbit(i))
        sum += c[i];
    return sum;
}
void PeekMedian() {
    int left = 1, right = maxn, mid, k = (s.size() + 1) / 2;
    while(left < right) {
        mid = (left + right) / 2;
        if(getsum(mid) >= k)
            right = mid;
        else
            left = mid + 1;
    }
    printf("%d\n", left);
}
int main() {
    int n, temp;
    scanf("%d", &n);
    char str[15];
    for(int i = 0; i < n; i++) {
        scanf("%s", str);
        if(str[1] == 'u') {
            scanf("%d", &temp);
            s.push(temp);
            update(temp, 1);
        } else if(str[1] == 'o') {
            if(!s.empty()) {
                update(s.top(), -1);
                printf("%d\n", s.top());
                s.pop();
            } else {
                printf("Invalid\n");
            }
        } else {
            if(!s.empty())
                PeekMedian();
            else
                printf("Invalid\n");
        }
    }
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55