树状数组解决的问题：

假如有这样一种情景，先输入一个长度为n的数组，然后我们有如下两种操作：

1. 输入一个数m，输出数组中下标1~m的前缀和
2. 对某个指定下标的数进行值的修改

多次执行上述两种操作；

常规方法

对于一个的数组，如果需要求1~m的前缀和我们可以将其从下标1开始对m个数进行求和，对于值的修改，我们可以直接通过下标找到要修改的数，然后更新前缀和，对于一次操作显然没什么问题，但对于$n$次操作，时间复杂度就达到了$O(n^2)$和$O(n)$，这样的方法就显得不适用了。

树状数组

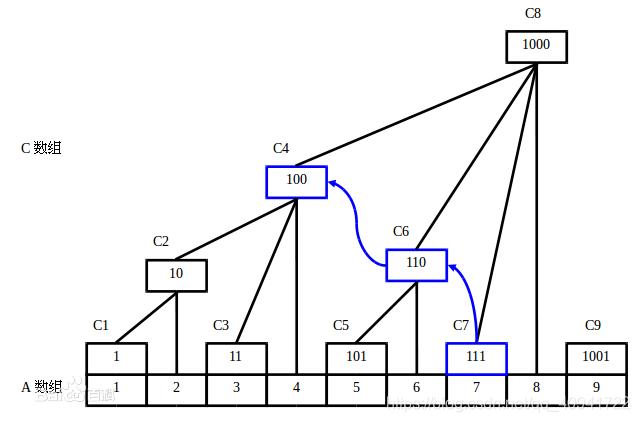
如图，对于一个长度为n的数组，A数组存放的是数组的初始值，引入一个辅助数组C；

C1 = A1
C2 = C1 + A2 = A1 + A2
C3 = A3
C4 = C2 + C3 + A4 = A1 + A2 + A3 + A4
C5 = A5
C6 = C5 + A6 = A5 + A6
C7 = A7
C8 = C4 + C6 + C7 + A8 = A1 + A2 + A3 + A4 + A5 + A6 + A7 + A8

我们称C[i]的值为下标为i的数所管辖的数的和，下标为i的数所管辖的元素的个数为$2^k$个（k为i的二进制的末尾0的个数），例如：

• i = 8 = 1000，末尾3个0，故k = 3，所管辖的个数为$2^3=8$，C8是8个数的和；
• i = 5 = 0101，末尾没有0，故k = 0，所管辖的个数为$2^0=1$，C5是一个数的和；

而对于输入的数m，我们要求编号为m的数的前缀和$A_1\cdots A_m$，按照上面说的，$su{m}_m=C_{}$