给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。

你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。

返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。

示例 1：

输入：[7,1,5,3,6,4]
输出：5
解释：在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
     注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格；同时，你不能在买入前卖出股票。

示例 2：

输入：prices = [7,6,4,3,1]
输出：0
解释：在这种情况下, 没有交易完成, 所以最大利润为 0。

提示：

• 1 <= prices.length <= 105
• 0 <= prices[i] <= 104

我们这题用动态规划进行求解，一系列的买卖股票问题都是可以用动态规划来解决，我们从买卖股票的最佳时机1开始理解，后面的就好写多了。动规五部曲（dp含义、递推公式、初始化、遍历顺序、打印数组）

那我们买卖股票的有两种状态，一种是持有一种不持有，所以我们定义二维数组dp[i][0]、和dp[i][1]，dp[i][0]表示第i天持有股票时手上所得的最大现金，dp[i][1]表示第i天不持有股票手上所得的最多现金。我们特别要注意一个点是，这里说到“持有”，不代表买入，我们dp[i][0]记录的是注意只是记录，记录第i天持有股票时手上所得的最大现金，而买入是一种结果，买入的话是不是会扣钱，买入某一天的股票则是-prices[i]，而是否真正的要买入则要比较，是不是最低价格的买入，以便后续最高利润卖出。

那我们来思考递推公式，如果第i天持有股票即dp[i][0]， 那么可以由两个状态推出来。
1.如果第i-1天就已经持有股票，持有股票就相当于买入，但只是相当于记录记录！并不是真正的买入，因为买入要最低价格的时候买入，我们每个dp[i][0]记录的是持有股票时最低价格，推导是最后dp[pricesSize-1][0]这个值就是真正买入的最低价格。dp[i-1][0]跟如果第i天买入（-prices[i]）进行比较，买入的之后手上的现金就肯定为负，这时候进行比较最大值（手上最大的现金），如果保持现状，所得现金就是昨天持有股票的所得现金 即：dp[i - 1][0]
2.如果第i天买入股票，所得现金就是买入今天的股票后所得现金即：-prices[i]

如果第i天不持有股票即dp[i][1],那么也是可以由两个状态推出来
1.第i-1天就不持有股票，那么就保持现状，所得现金就是昨天不持有股票的所得现金 即：dp[i - 1][1]
2.第i天卖出股票，所得现金就是按照今天股票价格卖出后所得现金利润即：prices[i] + dp[i - 1][0](卖出的是在前一天持有股票（dp[i-1][0]）前提下再加上今天股票的金额)

最后返回的是dp[pricesSize-1][1]而不是dp[pricesSize-1][0]，是为什么呢，因为最后不持有股票则是卖出了得到了利润。我们动态规划每一步缓存的都是手上得到的最大现金，一步步进行比较得出手上最大金钱延续到最后，最后的dp[pricesSize-1][0]得出的是真正买入时的最低价格是多少。dp[pricesSize-1][1]得出买入卖出的最大利润。



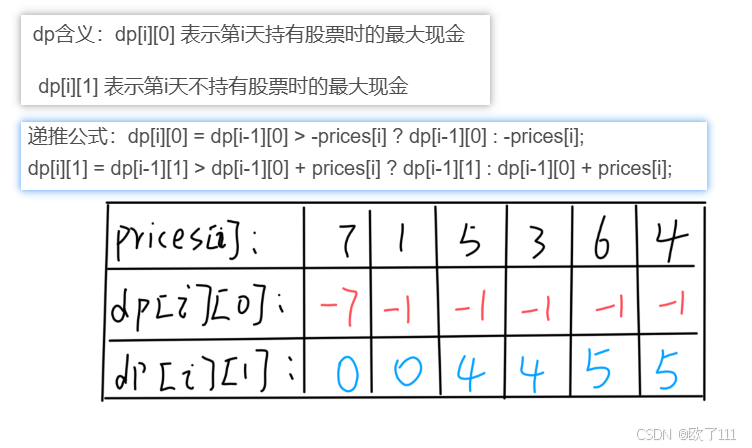
dp含义：dp[i][0] 表示第i天持有股票时的最大现金

 dp[i][1] 表示第i天不持有股票时的最大现金

初始化：我们持有股票是记录记录，所以第0天持有，记录下来的应该就是dp[0][0]= -prices[0]。
第0天不能卖出，即dp[0][1]=0，后面的就可以从前面的推导得出。

递推公式：dp[i][0] = dp[i-1][0] > -prices[i] ? dp[i-1][0] : -prices[i];
dp[i][1] = dp[i-1][1] > dp[i-1][0] + prices[i] ? dp[i-1][1] : dp[i-1][0] + prices[i];

遍历顺序：从前往后

打印数组：当遇到疑惑或者提交错误时，打印数组出来比较快速的看看哪一步有错。

以下是我在力扣c语言提交的代码，仅供参考：

int maxProfit(int* prices, int pricesSize) {
    // dp[i][0] 表示第i天持有股票时的最大现金
    // dp[i][1] 表示第i天不持有股票时的最大现金
    int dp[pricesSize+1][2];
 
    //初始化
    //记录第一天持有，现金为-prices[0]
    dp[0][0] = -prices[0];
    //第一天无法卖出，利润为0
    dp[0][1] = 0;
 
    for(int i = 1;i<pricesSize;i++)
    {
        // 第i天持有股票：要么之前已持有，要么当天买入（取较大值）
        dp[i][0] = dp[i-1][0] > -prices[i] ? dp[i-1][0] : -prices[i];
 
        // 第i天不持有股票：要么之前已卖出，要么当天卖出（利润为当天价格+前一天持有现金）
        dp[i][1] = dp[i-1][1] > dp[i-1][0] + prices[i] ? dp[i-1][1] : dp[i-1][0] + prices[i];
    }
 
    // 最大利润即为最后一天不持有股票的状态
    return dp[pricesSize-1][1];
}