一套图 搞懂“时间复杂度”

id="article_content" class="article_content clearfix"> id="content_views" class="htmledit_views">

写在前面：

这篇文章是在公众号： 程序员小灰 中发布的。是我到目前为止所看到的关于时间复杂度介绍的最好的文章，清晰明了。

所以拿来po出来 仅供学习交流，如侵则删。

现已将此文收录至： 《数据结构》C语言版 (清华严蔚敏考研版） 全书知识梳理

同类好文： 8种方法优雅地利用C++编程从1乘到20

                   从B站 (哔哩哔哩) 泄露的源码里发现了B站视频推荐的秘密

                   Facebook前身 哈佛“选美”网站 核心算法 --- ELO等级分制度(附源码)

正文： 

640?wx_fmt=jpeg

640?wx_fmt=jpeg

640?wx_fmt=jpeg

640?wx_fmt=jpeg

640?wx_fmt=jpeg

640?wx_fmt=jpeg

 

640?wx_fmt=png

时间复杂度的意义

 

究竟什么是时间复杂度呢？让我们来想象一个场景：某一天，小灰和大黄同时加入了一个公司......

640?wx_fmt=jpeg

一天过后，小灰和大黄各自交付了代码，两端代码实现的功能都差不多。大黄的代码运行一次要花100毫秒，内存占用5MB。小灰的代码运行一次要花100秒，内存占用500MB。于是......

640?wx_fmt=jpeg

640?wx_fmt=jpeg

由此可见，衡量代码的好坏，包括两个非常重要的指标：

1.运行时间；

2.占用空间。

640?wx_fmt=jpeg

640?wx_fmt=jpeg

 

640?wx_fmt=png

基本操作执行次数

 

关于代码的基本操作执行次数，我们用四个生活中的场景，来做一下比喻：

场景1：给小灰一条长10寸的面包，小灰每3天吃掉1寸，那么吃掉整个面包需要几天？

640?wx_fmt=jpeg

答案自然是 3 X 10 = 30天。

如果面包的长度是 N 寸呢？

此时吃掉整个面包，需要 3 X n = 3n 天。

如果用一个函数来表达这个相对时间，可以记作 T（n） = 3n。

场景2：给小灰一条长16寸的面包，小灰每5天吃掉面包剩余长度的一半，第一次吃掉8寸，第二次吃掉4寸，第三次吃掉2寸......那么小灰把面包吃得只剩下1寸，需要多少天呢？

这个问题翻译一下，就是数字16不断地除以2，除几次以后的结果等于1？这里要涉及到数学当中的对数，以2位底，16的对数，可以简写为log16。

因此，把面包吃得只剩下1寸，需要 5 X log16 = 5 X 4 = 20 天。

如果面包的长度是 N 寸呢？

需要 5 X logn = 5logn天，记作 T（n） = 5logn。

场景3：给小灰一条长10寸的面包和一个鸡腿，小灰每2天吃掉一个鸡腿。那么小灰吃掉整个鸡腿需要多少天呢？

640?wx_fmt=jpeg

答案自然是2天。因为只说是吃掉鸡腿，和10寸的面包没有关系 。

如果面包的长度是 N 寸呢？

无论面包有多长，吃掉鸡腿的时间仍然是2天，记作 T（n） = 2。

场景4：给小灰一条长10寸的面包，小灰吃掉第一个一寸需要1天时间，吃掉第二个一寸需要2天时间，吃掉第三个一寸需要3天时间.....每多吃一寸，所花的时间也多一天。那么小灰吃掉整个面包需要多少天呢？

答案是从1累加到10的总和，也就是55天。

如果面包的长度是 N 寸呢？

此时吃掉整个面包，需要 1+2+3+......+ n-1 + n = (1+n)*n/2 = 0.5n^2 + 0.5n。

记作 T（n） = 0.5n^2 + 0.5n。

640?wx_fmt=jpeg

上面所讲的是吃东西所花费的相对时间，这一思想同样适用于对程序基本操作执行次数的统计。刚才的四个场景，分别对应了程序中最常见的四种执行方式：

场景1：T（n） = 3n，执行次数是线性的。

  1.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="1">
class="hljs-ln-code"> class="hljs-ln-line">void eat1(int n){
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="2">
    • class="hljs-ln-code"> class="hljs-ln-line">    for(int i=0; i
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="3"> class="hljs-ln-code"> class="hljs-ln-line">        System.out.println("等待一天");
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="4"> class="hljs-ln-code"> class="hljs-ln-line">        System.out.println("等待一天");
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="5"> class="hljs-ln-code"> class="hljs-ln-line">        System.out.println("吃一寸面包");
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="6"> class="hljs-ln-code"> class="hljs-ln-line">    }
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="7"> class="hljs-ln-code"> class="hljs-ln-line">}
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="8"> class="hljs-ln-code"> class="hljs-ln-line">vo
    •  class="hljs-button signin active" data-title="登录复制" data-report-click="{"spm":"1001.2101.3001.4334"}" onclick="hljs.signin(event)">

    场景2：T（n） = 5logn，执行次数是对数的。

    1.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="1"> class="hljs-ln-code"> class="hljs-ln-line">void eat2(int n){
    2.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="2"> class="hljs-ln-code"> class="hljs-ln-line">   for(int i=1; i2){
    3.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="3"> class="hljs-ln-code"> class="hljs-ln-line">       System.out.println("等待一天");
    4.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="4"> class="hljs-ln-code"> class="hljs-ln-line">       System.out.println("等待一天");
    5.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="5"> class="hljs-ln-code"> class="hljs-ln-line">       System.out.println("等待一天");
    6.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="6"> class="hljs-ln-code"> class="hljs-ln-line">       System.out.println("等待一天");
    7.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="7"> class="hljs-ln-code"> class="hljs-ln-line">       System.out.println("吃一半面包");
    8.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="8"> class="hljs-ln-code"> class="hljs-ln-line">   }
    9.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="9"> class="hljs-ln-code"> class="hljs-ln-line">}
     class="hljs-button signin active" data-title="登录复制" data-report-click="{"spm":"1001.2101.3001.4334"}" onclick="hljs.signin(event)">

    场景3：T（n） = 2，执行次数是常量的。

    1.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="1"> class="hljs-ln-code"> class="hljs-ln-line">void eat3(int n){
    2.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="2"> class="hljs-ln-code"> class="hljs-ln-line">   System.out.println("等待一天");
    3.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="3"> class="hljs-ln-code"> class="hljs-ln-line">   System.out.println("吃一个鸡腿");
    4.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="4"> class="hljs-ln-code"> class="hljs-ln-line">}
     class="hljs-button signin active" data-title="登录复制" data-report-click="{"spm":"1001.2101.3001.4334"}" onclick="hljs.signin(event)">

    场景4：T（n） = 0.5n^2 + 0.5n，执行次数是一个多项式。

    1.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="1"> class="hljs-ln-code"> class="hljs-ln-line">void eat4(int n){
    2.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="2"> class="hljs-ln-code"> class="hljs-ln-line">   for(int i=0; i<n; i++){
    3.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="3"> class="hljs-ln-code"> class="hljs-ln-line">       for(int j=0; j<i; j++){
    4.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="4"> class="hljs-ln-code"> class="hljs-ln-line">           System.out.println("等待一天");
    5.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="5"> class="hljs-ln-code"> class="hljs-ln-line">       }
    6.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="6"> class="hljs-ln-code"> class="hljs-ln-line">       System.out.println("吃一寸面包");
    7.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="7"> class="hljs-ln-code"> class="hljs-ln-line">   }
    8.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="8"> class="hljs-ln-code"> class="hljs-ln-line">}
     class="hljs-button signin active" data-title="登录复制" data-report-click="{"spm":"1001.2101.3001.4334"}" onclick="hljs.signin(event)">

     

    640?wx_fmt=png

    渐进时间复杂度

     

    有了基本操作执行次数的函数 T（n），是否就可以分析和比较一段代码的运行时间了呢？还是有一定的困难。

    比如算法A的相对时间是T（n）= 100n，算法B的相对时间是T（n）= 5n^2，这两个到底谁的运行时间更长一些？这就要看n的取值了。

    所以，这时候有了渐进时间复杂度（asymptotic time complexity）的概念，官方的定义如下：

    若存在函数 f（n），使得当n趋近于无穷大时，T（n）/ f（n）的极限值为不等于零的常数，则称 f（n）是T（n）的同数量级函数。

    记作 T（n）= O（f（n）），称O（f（n）） 为算法的渐进时间复杂度，简称时间复杂度。

    渐进时间复杂度用大写O来表示，所以也被称为大O表示法。

    640?wx_fmt=jpeg

    640?wx_fmt=jpeg

    如何推导出时间复杂度呢？有如下几个原则：

    1. 如果运行时间是常数量级，用常数1表示；

    2. 只保留时间函数中的最高阶项；

    3. 如果最高阶项存在，则省去最高阶项前面的系数。

    让我们回头看看刚才的四个场景。

    场景1：

    T（n） = 3n 

    最高阶项为3n，省去系数3，转化的时间复杂度为：

    T（n） =  O（n）

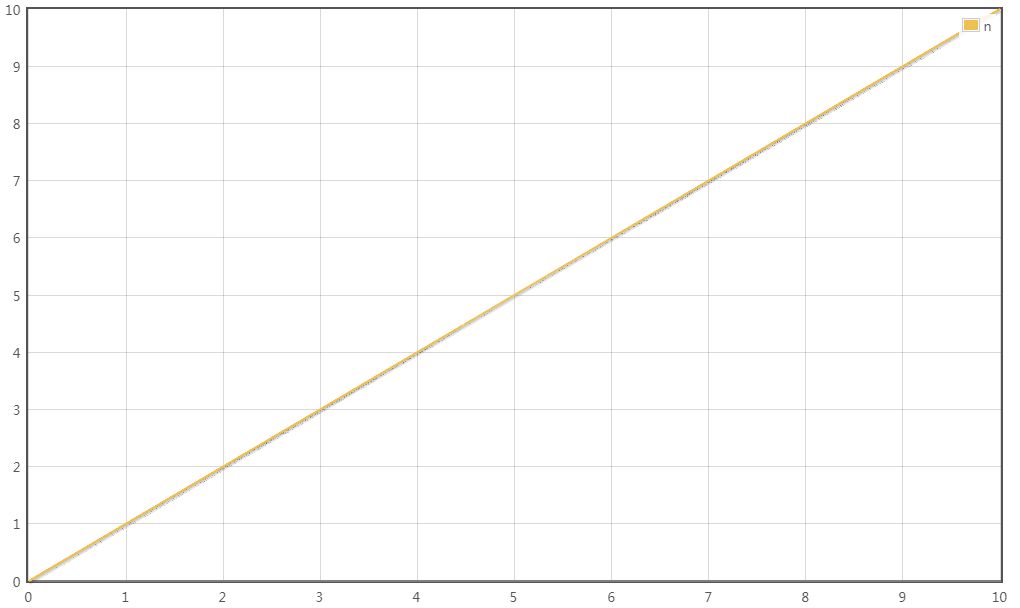
    640?wx_fmt=png

    场景2：

    T（n） = 5logn 

    最高阶项为5logn，省去系数5，转化的时间复杂度为：

    T（n） =  O（logn）

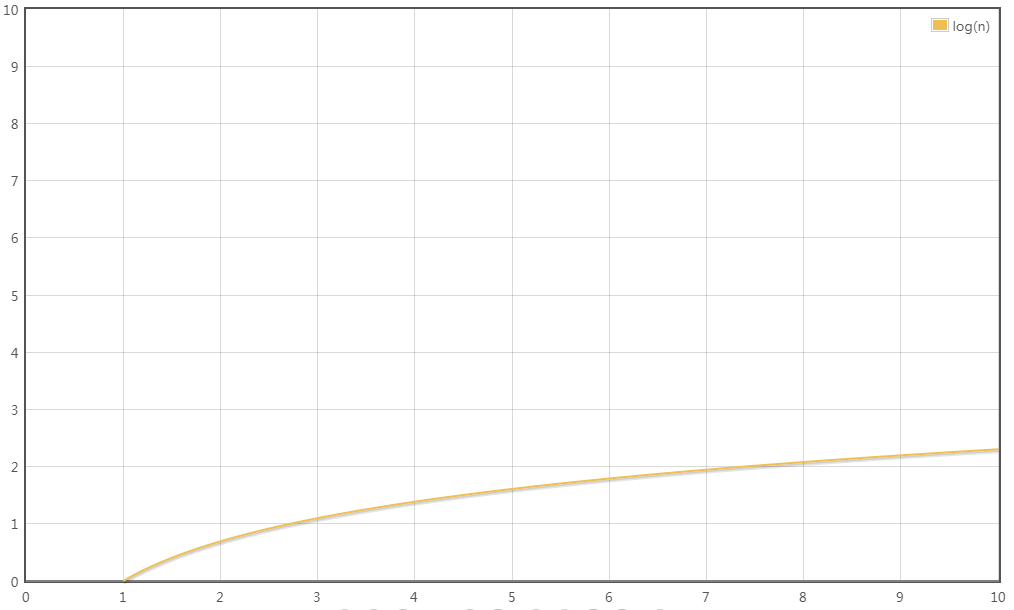
    640?wx_fmt=png

    场景3：

    T（n） = 2

    只有常数量级，转化的时间复杂度为：

    T（n） =  O（1）

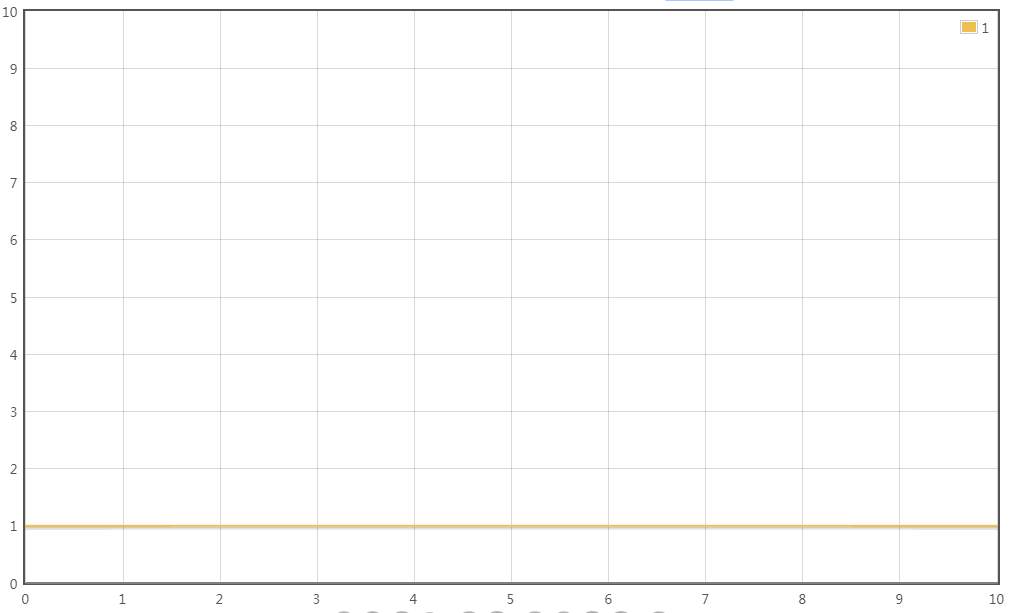
    640?wx_fmt=png

    场景4：

    T（n） = 0.5n^2 + 0.5n

    最高阶项为0.5n^2，省去系数0.5，转化的时间复杂度为：

    T（n） =  O（n^2）

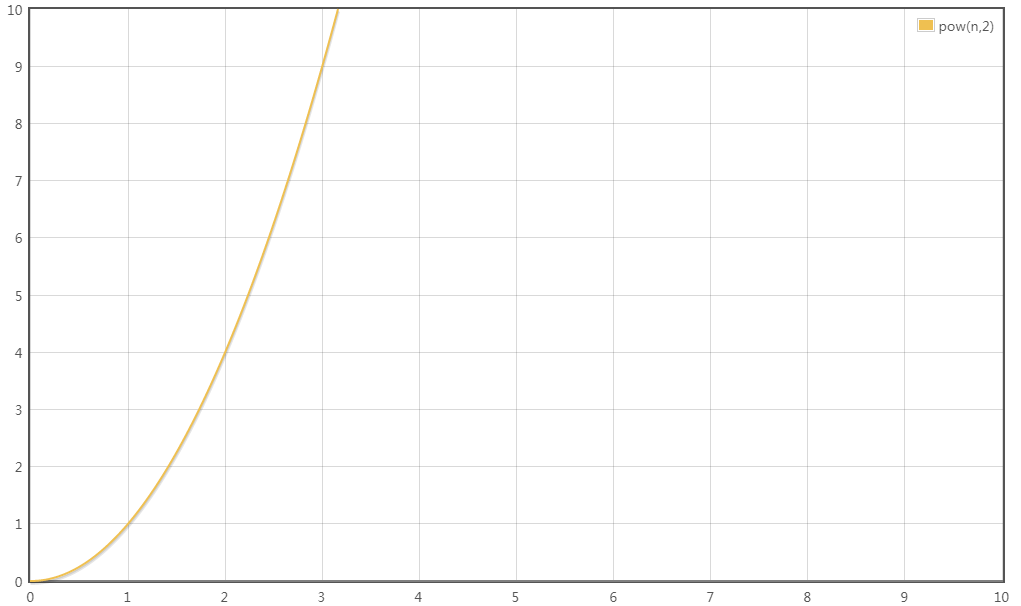
    640?wx_fmt=png

    这四种时间复杂度究竟谁用时更长，谁节省时间呢？稍微思考一下就可以得出结论：

    O（1）< O（logn）< O（n）< O（n^2）

    在编程的世界中有着各种各样的算法，除了上述的四个场景，还有许多不同形式的时间复杂度，比如：

    O（nlogn）, O（n^3）, O（m*n），O（2^n），O（n！）

    今后遨游在代码的海洋里，我们会陆续遇到上述时间复杂度的算法。

    640?wx_fmt=png

     

    640?wx_fmt=png

    时间复杂度的巨大差异

     

     

    640?wx_fmt=jpeg

    640?wx_fmt=jpeg

    我们来举过一个栗子：

    算法A的相对时间规模是T（n）= 100n，时间复杂度是O(n)

    算法B的相对时间规模是T（n）= 5n^2，时间复杂度是O(n^2)

    算法A运行在小灰家里的老旧电脑上，算法B运行在某台超级计算机上，运行速度是老旧电脑的100倍。

    那么，随着输入规模 n 的增长，两种算法谁运行更快呢？

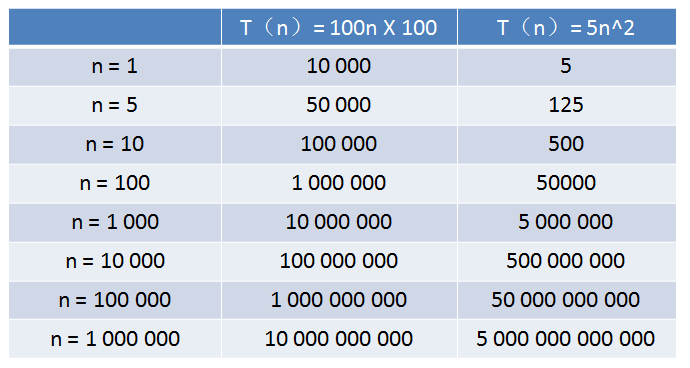
    640?wx_fmt=png

    从表格中可以看出，当n的值很小的时候，算法A的运行用时要远大于算法B；当n的值达到1000左右，算法A和算法B的运行时间已经接近；当n的值越来越大，达到十万、百万时，算法A的优势开始显现，算法B则越来越慢，差距越来越明显。

    这就是不同时间复杂度带来的差距。

    640?wx_fmt=jpeg

    如果感觉还不错，点个赞↗ 支持一下吧 ~

    随后还会不定期更新同类型文章，欢迎订阅关注我的博客 ~

    下一篇：400+条实用C/C++框架、库、工具整理 ，你能想到的都在这里了

    上一篇： Facebook前身 哈佛大学"选美"网站核心算法 -- ELO等级分制度(附源码)

    >>
    注：本文转载自blog.csdn.net的12 26 25的文章"https://blog.csdn.net/qq_41523096/article/details/82142747#comments"。版权归原作者所有，此博客不拥有其著作权，亦不承担相应法律责任。如有侵权，请联系我们删除。
    复制链接
    复制链接
    相关推荐
    发表评论

    评论记录：

    未查询到任何数据！