【数据结构】最大连续子序列和（四种算法逐级优化）

25-03-07 21:01

2655

7075

blog.csdn.net

id="article_content" class="article_content clearfix"> id="content_views" class="htmledit_views">

题目：

01-复杂度1 最大子列和问题（20 分）

给定K个整数组成的序列{ N1, N2, ..., NK }，“连续子列”被定义为{ Ni, Ni+1, ..., Nj }，其中 1≤i≤j≤K。“最大子列和”则被定义为所有连续子列元素的和中最大者。例如给定序列{ -2, 11, -4, 13, -5, -2 }，其连续子列{ 11, -4, 13 }有最大的和20。现要求你编写程序，计算给定整数序列的最大子列和。

本题旨在测试各种不同的算法在各种数据情况下的表现。各组测试数据特点如下：

数据1：与样例等价，测试基本正确性；
数据2：102个随机整数；
数据3：103个随机整数；
数据4：104个随机整数；
数据5：105个随机整数；

输入格式:

输入第1行给出正整数K (≤100000)；第2行给出K个整数，其间以空格分隔。

输出格式:

在一行中输出最大子列和。如果序列中所有整数皆为负数，则输出0。

输入样例:

 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="1">

class="hljs-ln-code"> class="hljs-ln-line">6

class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="2">

class="hljs-ln-code"> class="hljs-ln-line">-2 11 -4 13 -5 -2 class="hljs-button signin" data-title="登录后复制" data-report-click="{"spm":"1001.2101.3001.4334"}" onclick="hljs.signin(event)">

输出样例:

20 class="hljs-button signin" data-title="登录后复制" data-report-click="{"spm":"1001.2101.3001.4334"}" onclick="hljs.signin(event)">

作者: DS课程组

单位: 浙江大学

时间限制: 50000 ms

内存限制: 64 MB

代码长度限制: 16 KB

问题分析：

这道问题就是找出一个已给出的数列中最大的子列的和。如果当每个子列都为负数时输出为0（即最大子列和为负数时）。

解法一：穷举法（复杂度 O(N^3) )

把输入的数组，所有的子列都历遍，并从中找出最大

 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="1"> class="hljs-ln-code"> class="hljs-ln-line">#include 
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="2"> class="hljs-ln-code"> class="hljs-ln-line"> 
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="3"> class="hljs-ln-code"> class="hljs-ln-line">int main(){
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="4"> class="hljs-ln-code"> class="hljs-ln-line">	int K;//	输入K个数
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="5"> class="hljs-ln-code"> class="hljs-ln-line">	scanf("%d",&K);
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="6"> class="hljs-ln-code"> class="hljs-ln-line">	int max = 0;
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="7"> class="hljs-ln-code"> class="hljs-ln-line">	int a[K] = {0};
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="8"> class="hljs-ln-code"> class="hljs-ln-line">	for(int x = 0;x
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="9"> class="hljs-ln-code"> class="hljs-ln-line">	{
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="10"> class="hljs-ln-code"> class="hljs-ln-line">		scanf("%d",&a[x]);
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="11"> class="hljs-ln-code"> class="hljs-ln-line">	}
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="12"> class="hljs-ln-code"> class="hljs-ln-line">	
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="13"> class="hljs-ln-code"> class="hljs-ln-line">	for(int i=0;i
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="14"> class="hljs-ln-code"> class="hljs-ln-line">		for(int j=i;j
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="15"> class="hljs-ln-code"> class="hljs-ln-line">			int sum=0;//	求和 
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="16"> class="hljs-ln-code"> class="hljs-ln-line">		 	for(int m=i;m<=j;m++){
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="17"> class="hljs-ln-code"> class="hljs-ln-line">		 		sum += a[m];
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="18"> class="hljs-ln-code"> class="hljs-ln-line">			}
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="19"> class="hljs-ln-code"> class="hljs-ln-line">			if(sum > max){
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="20"> class="hljs-ln-code"> class="hljs-ln-line">				max = sum;
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="21"> class="hljs-ln-code"> class="hljs-ln-line">			}
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="22"> class="hljs-ln-code"> class="hljs-ln-line">		}
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="23"> class="hljs-ln-code"> class="hljs-ln-line">	}
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="24"> class="hljs-ln-code"> class="hljs-ln-line">	if(max < 0) {
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="25"> class="hljs-ln-code"> class="hljs-ln-line">		printf("0\n"); 
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="26"> class="hljs-ln-code"> class="hljs-ln-line">	}else{
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="27"> class="hljs-ln-code"> class="hljs-ln-line">		printf("%d\n",max); 
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="28"> class="hljs-ln-code"> class="hljs-ln-line">	}	
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="29"> class="hljs-ln-code"> class="hljs-ln-line">	
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="30"> class="hljs-ln-code"> class="hljs-ln-line">	return 0;
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="31"> class="hljs-ln-code"> class="hljs-ln-line">} class="hide-preCode-box"> class="hljs-button signin" data-title="登录后复制" data-report-click="{"spm":"1001.2101.3001.4334"}" onclick="hljs.signin(event)">

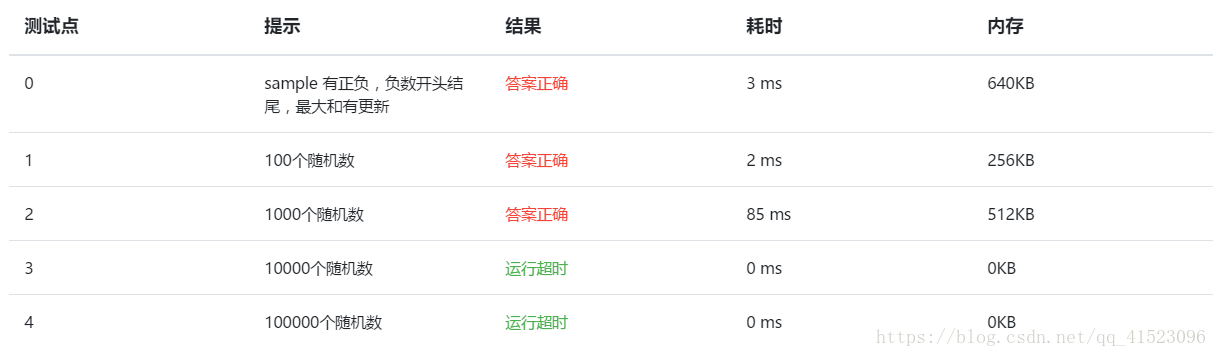
代码思路虽然简单，但是复杂度太大。当样例量级为10000时就超时了。

解法二：优化穷举（复杂度O(N^2) )

第一个算法的第三个for循环中有大量不必要的重复计算，如：计算i到j的和，然而i到j-1的和在前一次的循环中已经计算过，无需重复计算，故该for循环可以去掉

 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="1"> class="hljs-ln-code"> class="hljs-ln-line">#include 
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="2"> class="hljs-ln-code"> class="hljs-ln-line"> 
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="3"> class="hljs-ln-code"> class="hljs-ln-line">int main(){
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="4"> class="hljs-ln-code"> class="hljs-ln-line">	int K;//	输入K个数
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="5"> class="hljs-ln-code"> class="hljs-ln-line">	scanf("%d",&K);
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="6"> class="hljs-ln-code"> class="hljs-ln-line">	int max = 0;
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="7"> class="hljs-ln-code"> class="hljs-ln-line">	int a[K] = {0};
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="8"> class="hljs-ln-code"> class="hljs-ln-line">	for(int x = 0;x
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="9"> class="hljs-ln-code"> class="hljs-ln-line">	{
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="10"> class="hljs-ln-code"> class="hljs-ln-line">		scanf("%d",&a[x]);
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="11"> class="hljs-ln-code"> class="hljs-ln-line">	}
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="12"> class="hljs-ln-code"> class="hljs-ln-line">	
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="13"> class="hljs-ln-code"> class="hljs-ln-line">	for(int i=0;i
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="14"> class="hljs-ln-code"> class="hljs-ln-line">        int sum=0;
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="15"> class="hljs-ln-code"> class="hljs-ln-line">		for(int j=i;j
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="16"> class="hljs-ln-code"> class="hljs-ln-line">		 	sum += a[m];
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="17"> class="hljs-ln-code"> class="hljs-ln-line">			if(sum > max){
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="18"> class="hljs-ln-code"> class="hljs-ln-line">				max = sum;
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="19"> class="hljs-ln-code"> class="hljs-ln-line">			}
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="20"> class="hljs-ln-code"> class="hljs-ln-line">		}
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="21"> class="hljs-ln-code"> class="hljs-ln-line">	}
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="22"> class="hljs-ln-code"> class="hljs-ln-line">	if(max < 0) {
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="23"> class="hljs-ln-code"> class="hljs-ln-line">		printf("0\n"); 
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="24"> class="hljs-ln-code"> class="hljs-ln-line">	}else{
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="25"> class="hljs-ln-code"> class="hljs-ln-line">		printf("%d\n",max); 
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="26"> class="hljs-ln-code"> class="hljs-ln-line">	}	
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="27"> class="hljs-ln-code"> class="hljs-ln-line">	
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="28"> class="hljs-ln-code"> class="hljs-ln-line">	return 0;
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="29"> class="hljs-ln-code"> class="hljs-ln-line">} class="hide-preCode-box"> class="hljs-button signin" data-title="登录后复制" data-report-click="{"spm":"1001.2101.3001.4334"}" onclick="hljs.signin(event)">

虽然能够满足题目要求，但是N^2的复杂度依旧称不上是个好算法。所以还有没有更好的算法呢？

解法三：分治算法 (复杂度O(N*logN))

当遇到N^2 的算法时，应当考虑其能否化成O(N*logN)。

算法思想：把问题分成两个大致相等的子问题，然后递归地对它们求解，这是“分”的部分。“治”阶段将两个子问题的解修补到一起并可能再做些少量的附加工作，最后得到整个问题的解。

在该问题中，如果把序列从中间分为两部分，那么最大子序列和可能在三处出现，要么整个出现在输入数据的左半部，要么整个出现在右半部，要么跨越分界线。

前两种情况可以递归求解，第三种情况的最大和可以通过求出前半部分（包括前半部分的最后一个元素）的最大和以及后半部分（包含后半部分的第一个元素）的最大和而得到，此时将两个和相加。

//具体实现比较麻烦。

解法四：最优解法 --- 在线处理（复杂度 O（N））

深入问题的本质：极端化

其实，我们注意到，
当子列和sum 后一个项ai 相加时，只有当sum大于0时，此项加上sum之后才能增大，即才会有扩大子列和的可能。

反之当sum小于零时，可以直接舍弃，将sum变为零。(同时在这里隐含一个条件，就是当所有的项都是负数时，那么sum总是会为0，那么到最后的输出时可以直接输出sum）

 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="1"> class="hljs-ln-code"> class="hljs-ln-line">#include 
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="2"> class="hljs-ln-code"> class="hljs-ln-line"> 
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="3"> class="hljs-ln-code"> class="hljs-ln-line">int main(){
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="4"> class="hljs-ln-code"> class="hljs-ln-line">	int K;
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="5"> class="hljs-ln-code"> class="hljs-ln-line">	scanf("%d",&K);
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="6"> class="hljs-ln-code"> class="hljs-ln-line">	int max = 0;
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="7"> class="hljs-ln-code"> class="hljs-ln-line">	int a[K] = {0};
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="8"> class="hljs-ln-code"> class="hljs-ln-line">	for(int x = 0;x
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="9"> class="hljs-ln-code"> class="hljs-ln-line">	{
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="10"> class="hljs-ln-code"> class="hljs-ln-line">		scanf("%d",&a[x]);
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="11"> class="hljs-ln-code"> class="hljs-ln-line">	}
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="12"> class="hljs-ln-code"> class="hljs-ln-line">	int sum = 0;
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="13"> class="hljs-ln-code"> class="hljs-ln-line">	for(int i = 0;i < K;i++){
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="14"> class="hljs-ln-code"> class="hljs-ln-line">		sum += a[i];
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="15"> class="hljs-ln-code"> class="hljs-ln-line">		if(sum > max){
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="16"> class="hljs-ln-code"> class="hljs-ln-line">			max = sum; 
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="17"> class="hljs-ln-code"> class="hljs-ln-line">		}else if(sum < 0){
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="18"> class="hljs-ln-code"> class="hljs-ln-line">			sum = 0;
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="19"> class="hljs-ln-code"> class="hljs-ln-line">		}
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="20"> class="hljs-ln-code"> class="hljs-ln-line">	}
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="21"> class="hljs-ln-code"> class="hljs-ln-line">		printf("%d\n",max); 
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="22"> class="hljs-ln-code"> class="hljs-ln-line">	
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="23"> class="hljs-ln-code"> class="hljs-ln-line">	return 0;
 class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="24"> class="hljs-ln-code"> class="hljs-ln-line">} class="hide-preCode-box"> class="hljs-button signin" data-title="登录后复制" data-report-click="{"spm":"1001.2101.3001.4334"}" onclick="hljs.signin(event)">

>>

注：本文转载自blog.csdn.net的12 26 25的文章"https://iamlzy.blog.csdn.net/article/details/83032032"。版权归原作者所有，此博客不拥有其著作权，亦不承担相应法律责任。如有侵权，请联系我们删除。

复制链接

发表评论

注册

评论记录：

未查询到任何数据！