该篇博客为课程学习的笔记,含一个例子可以帮助理解蚁群算法,主要为理论知识的总结。
蚁群算法详解
1.算法简介
1991年意大利米兰理学院M. Dorigo提出Ant System, 用于求解TSP等组合优化问题,这是一种模拟蚂蚁觅食行为的优化算法。
蚂蚁在运动过程中, 能够在它所经过的路径上留下外激素,而且蚂蚁在运动过程中能够感知外激素的存在及其强度,并以此指导自己的运动方向, 蚂蚁倾向于朝着外激素强度高的方向移动.由大量蚂蚁组成的蚁群的集体行为便表现出一种信息正反馈现象: 某一路径上走过的蚂蚁越多,则后来者选择该路径的概率就越大. 蚂蚁个体之间就是通过这种信息的交流达到搜索食物的目的。
举一个例子来进行说明:
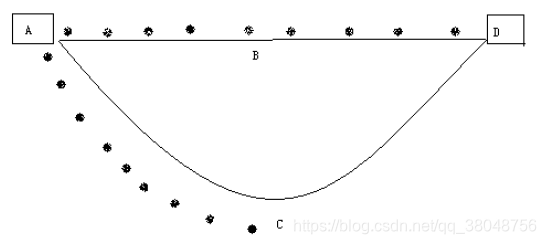
蚂蚁从A点出发,速度相同,食物在D点,可能随机选择路线ABD或ACD。假设初始时每条分配路线一只蚂蚁,每个时间单位行走一步,本图为经过9个时间单位时的情形:走ABD的蚂蚁到达终点,而走ACD的蚂蚁刚好走到C点,为一半路程。
经过18个时间单位时的情形:走ABD的蚂蚁到达终点后得到食物又返回了起点A,而走ACD的蚂蚁刚好走到D点。
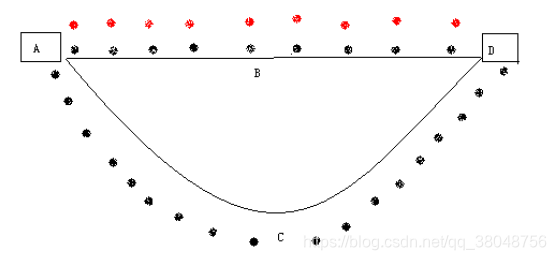
假设蚂蚁每经过一处所留下的信息素为一个单位,则经过36个时间单位后,所有开始一起出发的蚂蚁都经过不同路径从D点取得了食物,此时ABD的路线往返了2趟,每一处的信息素为4个单位,而ACD的路线往返了一趟,每一处的信息素为2个单位,其比值为2:1
寻找食物的过程继续进行,则按信息素的指导,蚁群在ABD路线上增派一只蚂蚁(共2只),而ACD路线上仍然为一只蚂蚁。再经过36个时间单位后,两条线路上的信息素单位积累为12和4,比值为3:1。
若按以上规则继续,蚁群在ABD路线上再增派一只蚂蚁(共3只),而ACD路线上仍然为一只蚂蚁。再经过36个时间单位后,两条线路上的信息素单位积累为24和6,比值为4:1。
若继续进行,则按信息素的指导,最终所有的蚂蚁会放弃ACD路线,而都选择ABD路线。这也就是前面所提到的正反馈效应。
基于以上蚁群寻找食物时的最优路径选择问题,可以构造人工蚁群,来解决最优化问题,如TSP问题。
人工蚁群和自然蚁群的区别:
- 人工蚁群有一定的记忆能力,能够记忆已经访问过的节点;
- 人工蚁群选择下一条路径的时候是按一定算法规律有意识地寻找最短路径,而不是盲目的。例如在TSP问题中,可以预先知道当前城市到下一个目的地的距离。

2.Ant System(蚂蚁系统)
蚂蚁系统是以TSP作为应用实例提出的,是最基本的ACO(Ant Colony algorithm)算法,下面以AS求解TSP问题的基本流程为例描述蚁群优化算法的工作机制
首先对于TSP问题的数学模型如下:

AS算法求解TSP问题有两大步骤:路径构建与信息素更新方式。
2.1 路径构建
每个蚂蚁都随机选择一个城市作为其出发城市,并维护一个路径记忆向量,用来存放该蚂蚁依次经过的城市。 蚂蚁在构建路径的每一步中,按照一个随机比例规则选 择下一个要到达的城市。
随机比例规则如下:

2.2 信息素更新

此处的
C
n
n
C^{nn}
Cnn表示最短路径的长度。
为了模拟蚂蚁在较短路径上留下更多的信息素,当所有蚂蚁到达终点时,必须把各路径的信息素浓度重新更新一次,信息素的更新也分为两个部分:
首先,每一轮过后,问题空间中的所有路径上的信息素都会发生蒸发,然后,所有的蚂蚁根据自己构建的路径长度在它们本轮经过的边上释放信息素


信息素挥发(evaporation)信息素痕迹的挥发过程是每个连接上的信息素痕迹的浓度自动逐渐减弱的过程,这个挥发过程主要用于避免算法过快地向局部最优区域集中,有助于搜索区域的扩展。
信息素增强(reinforcement)增强过程是蚁群优化算法中可选的部分,称为离线更新方式(还有在线更新方式)。这种方式可以实现 由单个蚂蚁无法实现的集中行动。基本蚁群算法的离线更新方式是在蚁群中的m只蚂蚁全部完成n城市的访问后,统一对残留信息进行更新处理。
下面以一个例子进行说明:

其中矩阵D表示各城市间的距离





一般蚁群算法的框架和上述算法大致相同,有三个组成部分:蚁群的活动;信息素的挥发;信息素的增强;主要体现在转移概率公式和信息素更新公式的不同。
3. 改进的蚁群算法
上述基本的AS算法,在不大于75城市的TSP中,结果还是较为理想的,但是当问题规模扩展时, AS的解题能力大幅度下降。进而提出了一些改进版本的AS算法,这些AS改进版本的一个共同点就是增强了蚂蚁搜索过程中对最优解的探索能力,它们之间的差异仅在于搜索控制策略方面。
3.1 精英策略的蚂蚁系统(Elitist Ant System, EAS)
- AS算法中,蚂蚁在其爬过的边上释放与其构建路径长度成反比的信息素量,蚂蚁构建的路径越好,则属于路径的各个边上的所获得的信息素量就越多,这些边以后在迭代中被蚂蚁选择的概率也就越大。
- 我们可以想象,当城市的规模较大时,问题的复杂度呈指数级增长,仅仅靠这样一个基础单一的信息素更新机制引导搜索偏向,搜索效率有瓶颈。
因而精英策略(Elitist Strategy) 被提出,这是一种较早的改进方法,通过一种“额外的手段”强化某些最有可能成为最优路径的边,让蚂蚁的搜索范围更快、更正确的收敛。
- 在算法开始后即对所有已发现的最好路径给予额外的增强,并将随后与之对应的行程记为Tb(全局最优行程);
- 当进行信息素更新时,对这些行程予以加权,同时将经过这些行程的蚂蚁记为“精英”,从而增大较好行程的选择机会。
其信息素的更新方式如下:

3.2 基于排列的蚂蚁系统(Rank-based AS, ASrank )
精英策略被提出后,人们提出了在精英策略的基础上,对其余边的信息素更新机制加以改善

3.3 最大最小蚂蚁系统(MAX-MIN Ant System, MMAS)
首先思考几个问题:
问题一:对于大规模的TSP,由于搜索蚂蚁的个数有限,而初始化时蚂蚁的分布是随机的,这会不会造成蚂蚁只搜索了所有路径 中的小部分就以为找到了最好的路径,所有的蚂蚁都很快聚集在 同一路径上,而真正优秀的路径并没有被搜索到呢?
问题二:当所有蚂蚁都重复构建着同一条路径的时候,意味着算法的已经进入停滞状态。此时不论是基本AS、EAS还是ASrank , 之后的迭代过程都不再可能有更优的路径出现。这些算法收敛的 效果虽然是“单纯而快速的”,但我们都懂得欲速而不达的道理, 我们有没有办法利用算法停滞后的迭代过程进一步搜索以保证找 到更接近真实目标的解呢?
对于MAX-MIN Ant System
1.该算法修改了AS的信息素更新方式,只允许迭代最优蚂蚁(在本次迭代构建出最短路径的蚂蚁),或者至今最优蚂蚁释放信息素;
2.路径上的信息素浓度被限制在[MAX,MIN ]范围内;
3.另外,信息素的初始值被设为其取值上限,这样有助于增加算法初始阶段的搜索能力。
4.为了避免搜索停滞,问题空间内所有边上的信息素都会被重新初始化。
改进1借鉴于精华蚂蚁系统,但又有细微的不同。
- 在EAS中,只允许至今最优的蚂蚁释放信息素,而在MMAS中,释放信息素的不仅有可能是至今最优蚂蚁,还有可能是迭代最优蚂蚁。
- 实际上,迭代最优更新规则和至今最优更新规则在MMAS中是交替使用的。
- 这两种规则使用的相对频率将会影响算法的搜索效果。
- 只使用至今最优更新规则进行信息素的更新,搜索的导向性很强,算法会很快的收敛到Tb附近;反之,如果只使用迭代最优更新规则,则算法的探索能力会得到增强,但搜索效率会下降。
改进2是为了避免某些边上的信息素浓度增长过快,出现算法早熟现象。
- 蚂蚁是根据启发式信息和信息素浓度选择下一个城市的。
- 启发式信息的取值范围是确定的。
- 当信息素浓度也被限定在一个范围内以后,位于城市i的蚂蚁k选择城市j作为下一个城市的概率pk(i,j)也将被限制在一个区间内。
改进3,使得算法在初始阶段,问题空间内所有边上的信息素均被初始化τmax的估计值,且信息素蒸发率非常小(在MMAS中,一般将蒸发率设为0.02)。
- 算法的初始阶段,不同边上的信息素浓度差异只会缓慢的增加,因此,MMAS在初始阶段有着较基本AS、EAS和ASrank更强搜索能力。
- 增强算法在初始阶段的探索能力有助于蚂蚁“视野开阔地”进行全局范围内的搜索,随后再逐渐缩小搜索范围,最后定格在一条全局最优路径上。
之前的蚁群算法,包括AS、EAS以及ASrank,都属于“一次性探索”,即随着算法的执行,某些边上的信息素量越来越小,某些路径被选择的概率也越来越小,系统的探索范围不断减小直至陷入停滞状态。
- MMAS中改进4,当算法接近或者是进入停滞状态时,问题空间内所有边上的信息素浓度都将被初始化,从而有效的利用系统进入停滞状态后的迭代周期继续进行搜索,使算法具有更强的全局寻优能力。
4.蚁群系统(Ant Colony System)
上述EAS、ASrank 以及MMAS都是对AS进行了少量的修改而获得了更好的性能。1997年,蚁群算法的创始人Dorigo在Ant colony system:a cooperative learning approach to the traveling salesman problem一文中提出了一种新的具有全新机制的ACO 算法——蚁群系统,是蚁群算法发展史上的又一里程碑。
ACS与AS之间存在三方面的主要差异:
1.使用一种伪随机比例规则选择下一个城市节点, 建立开发当前路径与探索新路径之间的平衡。
2.信息素全局更新规则只在属于至今最优路径的边上蒸发和释放信息素。
3.新增信息素局部更新规则,蚂蚁每次经过空间内的某条边,他都会去除该边上的一定量的信息素,以增加后续蚂蚁探索其余路径的可能性。



5.算法应用

背包问题





系数的确定:

蚁群大小:
一般情况下蚁群中蚂蚁的个数不超过TSP图中节点的个数。
终止条件:
1 给定一个外循环的最大数目,表明已经有足够的蚂蚁工作;
2 当前最优解连续K次相同而停止,其中K是一个给定的整数,表示算法已经收敛,不再需要继续;
3 目标值控制规则,给定优化问题(目标最小化)的一个下界和一个误差值,当算法得到的目标值同下界之差小于给定的误差值时,算法 终止。
信息素的更新分为离线和在线两种方式。
离线方式(同步更新方式):在若干只蚂蚁完成n个城市的访问后,统一对残留信息进行更新处理。
信息素的在线更新(异步更新方式):蚂蚁每行走一步,立即回溯并且更新行走路径上的信息素。


EAS算法是典型的离线信息素更新方式。该算法中,蚁群中蚂蚁的先后出行顺序没有相关性,但是每次循环需要记忆m只蚂蚁的行走路径,以进行比较选择最优路径。相对而言,单蚂蚁离线更 新方式记忆信息少,只需要记忆第s只蚂蚁的路径,并通过信息素更新后,释放该蚂蚁的所有记录信息。实际上这种方式等价于蚁 群离线方式中只有一只蚂蚁。


小结:
随着群智能理论和应用算法研究的不断发展,研究者已尝试着将其用于各种工程优化问题,并取得了意想不到的收获。多种研究表明,群智能在离散求解空间和连续求解空间中均表现出良好的搜索效果,并在组合优化问题中表现突出。
蚁群优化算法并不是旅行商问题的最佳解决方法,但是它却为解决组合优化问题提供了新思路,并很快被应用到其它组合优化问题中。比较典型的应用研究包括:网络路由优化、数据挖掘以及一些经典的组合优化问题。
附:蚁群算法的应用场景
蚁群算法在电信路由优化中的应用:
蚁群算法在电信路由优化中已取得了一定的应用成果。HP公司和英国电信公司在90年代中后期都开展了这方面的研究,设计了蚁群路由算法(Ant Colony Routing, ACR)。每只蚂蚁就像蚁群优化算法中一样,根据它在网络上的经验与性能,动态更新路由表项。如果一只蚂蚁因为经过了网络中堵塞的路 由而导致了比较大的延迟,那么就对该表项做较大的增强。同时根 据信息素挥发机制实现系统的信息更新,从而抛弃过期的路由信息。 这样,在当前最优路由出现拥堵现象时,ACR算法就能迅速的搜寻另一条可替代的最优路径,从而提高网络的均衡性、负荷量和利用 率。目前这方面的应用研究仍在升温,因为通信网络的分布式信息 结构、非稳定随机动态特性以及网络状态的异步演化与ACO的算法本质和特性非常相似。
蚁群算法聚类问题的应用:
基于群智能的聚类算法起源于对蚁群蚁卵的分类研究。Lumer和Faieta将Deneubourg提出将蚁巢分类模型应用于数据聚类分析。其基本思想是将待聚类数据随机地散布到一个二维平面内,然后 将虚拟蚂蚁分布到这个空间内,并以随机方式移动,当一只蚂蚁 遇到一个待聚类数据时即将之拾起并继续随机运动,若运动路径 附近的数据与背负的数据相似性高于设置的标准则将其放置在该 位置,然后继续移动,重复上述数据搬运过程。按照这样的方法 可实现对相似数据的聚类。
蚁群算法在组合优化问题中的应用:
ACO还在许多经典组合优化问题中获得了成功的应用,如二次规划问题(QAP)、机器人路径规划、作业流程规划、图着色(Graph Coloring)等问题。 经过多年的发展,ACO已成为能够有效解决实际二次规划问题的几种重要算法之一。AS在作业流程计划(Job-shop Scheduling)问题中的应用实例已经出现,这说明了AS在此领域的应用潜力。利用MAX-MIN AS解决QAP也取得了比较理想的效果,并通过实验中的计算数据证明采用该方法处理QAP比较早的SA算法更好,且与禁忌搜索算法性能相当。利用ACO实现对生产流程和特料管理的综合优化,并通过与遗传、模拟退火和禁忌搜索算法的比较证明了ACO的工程应用价值。
其他应用方面:
武器攻击目标分配和优化问题
车辆运行路径规划
区域性无线电频率自动分配
Bayesian networks的训练
集合覆盖
Costa和Herz还提出了一种AS在规划问题方面的扩展应用——图着色问题,取得了与其他启发式算法相似的效果。
推荐:
蚁群算法其他优秀博客
https://blog.csdn.net/qq_33829154/article/details/85258615

评论记录:
回复评论: