一、题目

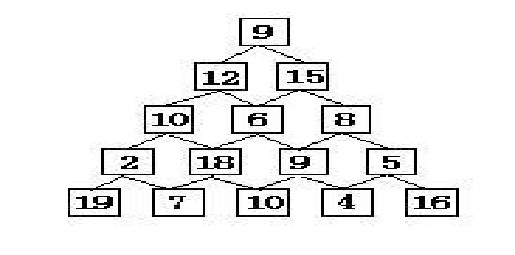
数塔问题 ：要求从顶层走到底层，若每一步只能走到相邻的结点，则经过的结点的数字之和最大是多少？

二、解题思路

     动态规划解题思路可详见另一篇文章。数塔中元素用二维数组a[][]表示

①定义状态

由题意可设dp[i][j]为第i层的第j个顶点到底层经过的最大数字和。

②定义状态转移方程

大家知道动态规划满足无后向性，即：每个阶段的决策仅受之前决策的影响，但是不影响之后各阶段的决策。所以我们可以从后往前推出状态转移方程（逆向思维），dp[0][0]等于第1层第1个数字到底层经过的最大数字和，它等于dp[1][0] + a[0][0]或dp[1][1] + a[0][0]中的最大的数值。我们可以公式化，得到如下状态转换方程：

         dp[i][j] = max( dp[i+1][j] + dp[i+1][j+1] ) + a[i][j]

③确定边界

由状态定义我们可以得出当数字在最底层时，它到最底层就是数字本身，即可得出dp[i][j] = a[i][j] (0≤i,j≤N)

三、代码编写

#include 
#include 
 
#define N 5
#define max(a,b) ((a>b)?a:b)
 
int main()
{
    //保存数塔元素
    int a[N][N] = { {9,0,0,0,0},
                    {12,15,0,0,0},
                    {10,6,8,0,0},
                    {2,18,9,5,0},
                    {19,7,10,4,16}};
    //dp[i][j]为第i层的第j个顶点到底层经过的最大数字和
    int dp[N][N] = {0};
    //确定边界数值
    int i,j;
    for(i=0;i < N;i++){
        dp[N-1][i] = a[N-1][i];
    }
    //核心算法
    for(i=N-2;i >= 0;i--){
        for(j=0; j < i+1 ;j++){
            dp[i][j] = max(dp[i+1][j],dp[i+1][j+1]) + a[i][j];
        }
    }
 
    printf("DP矩阵为：\n");
    for(i=0;i < N;i++){
        for(j=0; j <= i ;j++){
             printf("%d ",dp[i][j]);
        }
        printf("\n");
    }
    printf("顶层到底层的经过的最大数字和为：%d",dp[0][0]);
    return 0;
}

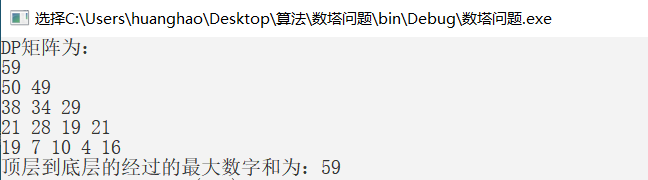
四、运行结果

五、总结

动态规划需要满足无后向性，可用逆向思维推出状态转化方程，动态规划解题方法可详见另一篇文章。