一、引言

  视频图像缩放技术在数字图像处理领域中有着广泛的应用。现在各种液晶设备的分辨率不同，视频图像输入的分辨率也各不相同，想要在显示器上正确的显示出相应图像画面，就必须对输入的图像大小进行缩放调整到显示屏支持的分辨率。
图像缩放算法有很多种，常见的包括：

1. 最近邻插值（Nearest Neighbor Interpolation）：

   • 优点：简单快速，计算量小。
   • 缺点：放大时会出现锯齿现象，质量较差。

2. 双线性插值（Bilinear Interpolation）：

   • 优点：较为简单，质量较高，图像平滑。
   • 缺点：计算量较大，处理边缘时可能出现模糊。

3. 双三次插值（Bicubic Interpolation）：

   • 优点：质量较高，图像平滑，边缘保持较好。
   • 缺点：计算量更大，可能引入一些伪影。

4. Lanczos插值（Lanczos Resampling）：

   • 优点：质量较高，抗锯齿能力强。
   • 缺点：计算量大，处理速度较慢。

5. Lanczos插值的变种，如Lanczos-2、Lanczos-3等：

   • 优点：在一定程度上平衡了计算量和质量。
   • 缺点：可能有些许伪影。

  主流使用的缩放算法通常是双线性插值和双三次插值。双线性插值在实现简单的同时质量较高，适合一般性的图像缩放需求；双三次插值在质量上更为优秀，能够更好地保持图像细节，但计算量较大，适合对图像质量要求较高的场景。

二、双线性插值缩放算法原理

2.1 线性插值推导

  在学习双线性之前，我们先来想一下：什么是线性？从中学时代大家都接触过一元一次方程，线性方程等等。老师解释的是：线性指量与量之间按比例、成直线的关系，在数学上可以理解为一阶导数为常数的函数；非线性则指不按比例、不成直线的关系，一阶导数不为常数。

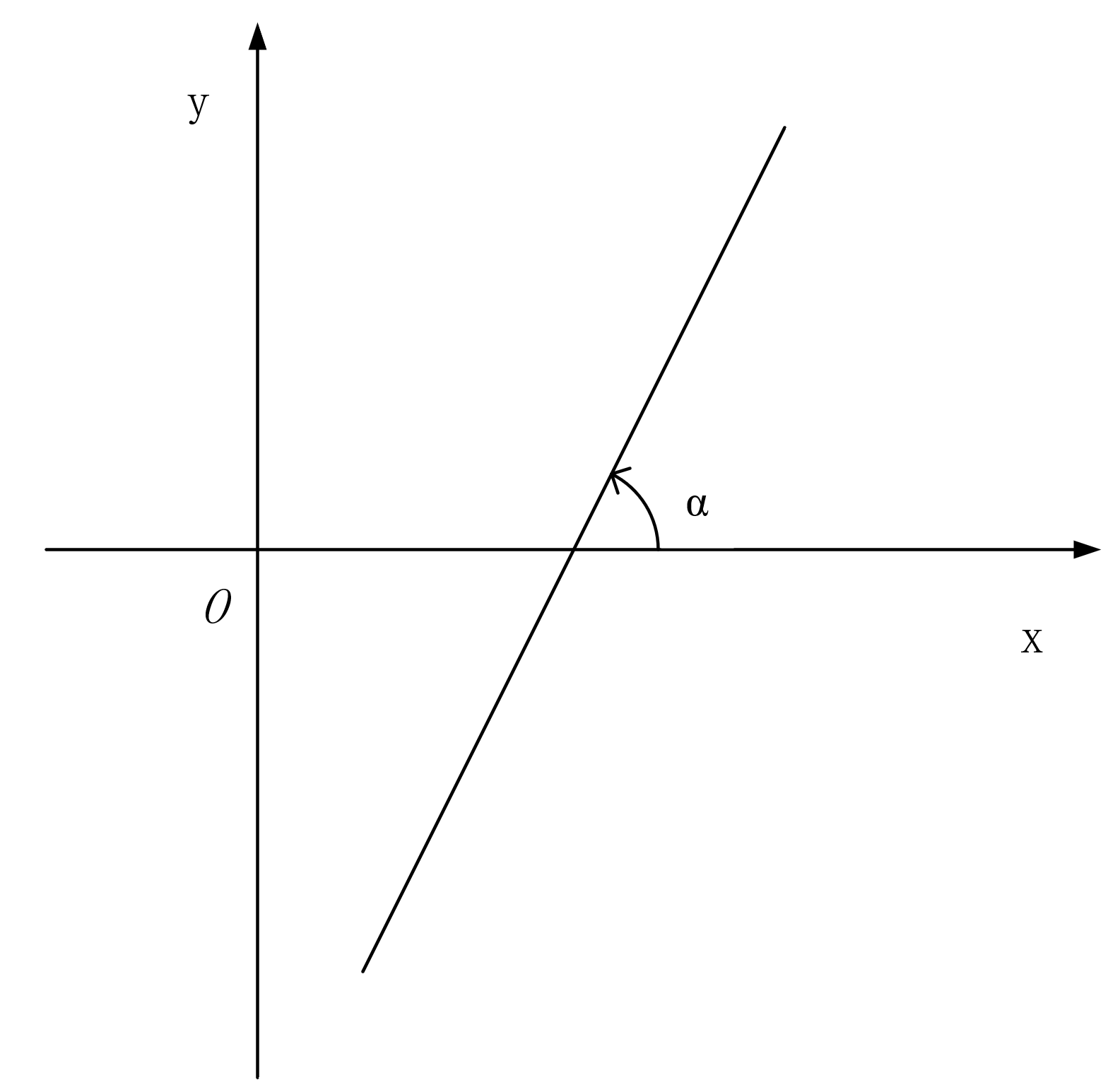
  如上图所示，就是线性的函数。已知一个线性的函数方程，我们就能求出该直线上任意一点的值。比如已知直线方程 y=2x，我们就能求出x=1时，y=2、x=2时，y=4等等。
中学时候学过两点式直线方程，已知两点坐标就可以确定一条直线，公式为：

$$\frac{x-x_1}{x_2-x_1}+\frac{y-y_1}{y_2-y_1}$$
  因此，我们就能通过已经知道的两个点，求出在该直线上的所有点的值，比如已知A的坐标(x1，y1)，B的坐标(x2，y2)，求出 [x1, x2] 区间内某一位置 x 在直线上的y值

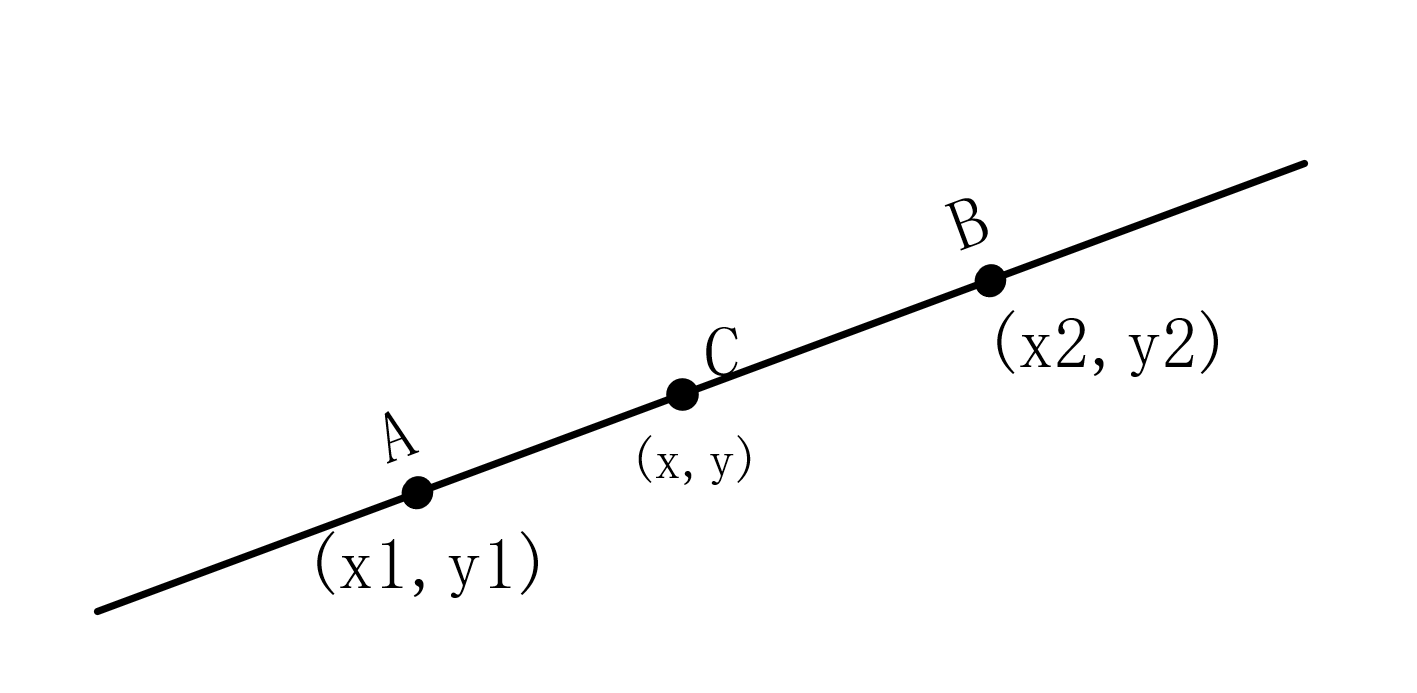
  公式变换一下就得到：
$$\frac{y-y_1}{y_2-y_1}=\frac{x-x_1}{x_2-x_1}$$
  化简可得：
$$y=\frac{x_2-x}{x_2-x_1}{y}_1+\frac{x-x_1}{x_2-x_1}{y}_2$$
  就能通过两点的坐标，求出 x 所在位置的值y，这就是线性插值

2.2 双线性插值推导

  双线性插值的意思就是：在两个方向上都进行线性插值。

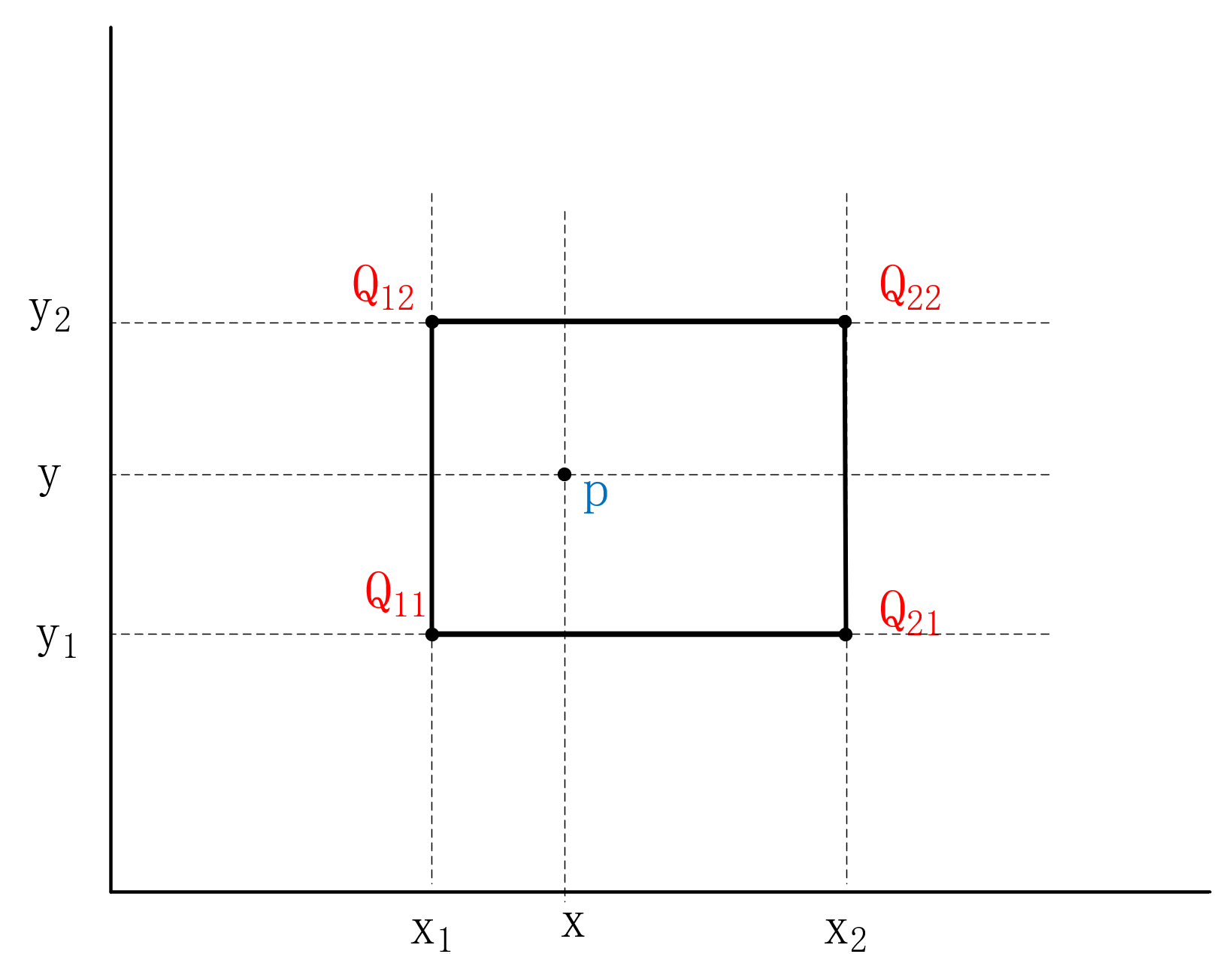
  已知四个点 Q11、Q12、Q21、Q22四个点的坐标所在的值，如何求P点坐标(x,y)的值。P点既不在Q11与Q22连线上，也不在Q12与Q21连线上，所以只用一次线性插值是不行的。我们可以在X方向，Y方向都使用一次线性插值，如下图所示：

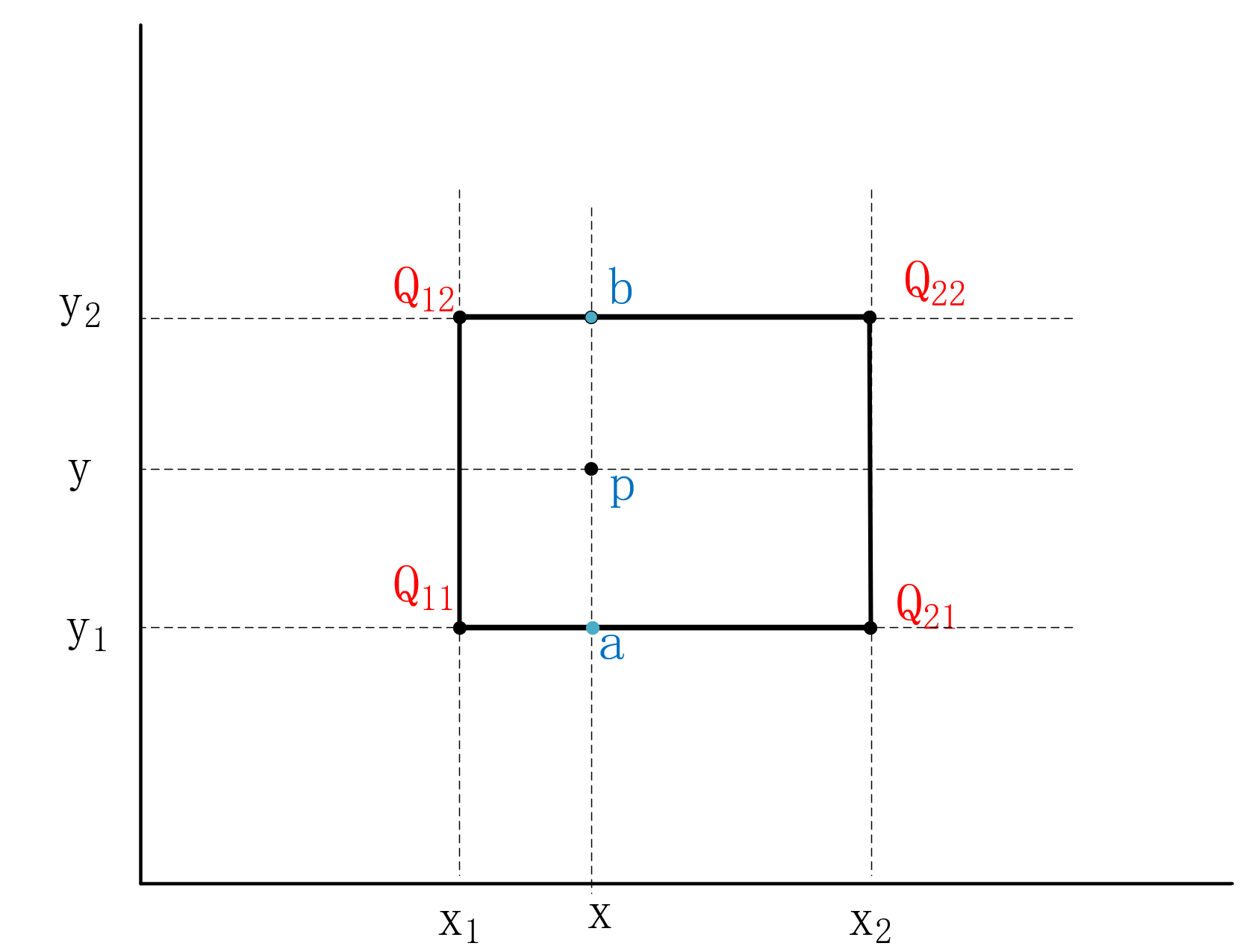
1. 第一步，在横向（X轴方向）在Q11与Q21直线之间用一次线性插值，求出x位置所在的a点的值。
2. 第二步，在横向（X轴方向）在Q12与Q22直线之间用一次线性插值，求出x位置所在的b点的值。
3. 第三步，在纵向（Y轴方向）在a与b直线之间用一次线性插值，求出y位置所在的p点的值。

公式如下：
  假如我们想得到未知函数 $f$ 在点P= (x，y)的值，假设我们已知函数 在Q11 (x1,y1)，Q12 (x1, y2), Q21 (x2,y1),及Q22 (x2,y2)四个点的值

• 首先在x方向进行线性插值，得到：
  $$f(a)=\frac{x_2-x}{x_2-x_1}f(Q_{11})+\frac{x-x_1}{x_2-x_1}f(Q_{21})$$
  $$f(b)=\frac{x_2-x}{x_2-x_1}f(Q_{12})+\frac{x-x_1}{x_2-x_1}f(Q_{22})$$
• 再在y方向进行线性插值，得到：

$$f(p)=\frac{y_2-y}{y_2-y_1}f(a)+\frac{y-y_1}{y_2-y_1}f(b)$$

• 最后，将$f(a)$与$f(b)$带入可得到：
  $$f(p)=f(x,y)=\frac{f(Q_{11})}{(x_2-x_1)(y_2-y_1)}(x_2-x)(y_2-y)+\frac{f(Q_{21})}{(x_2-x_1)(y_2-y_1)}(x-x_1)(y_2-y)$$
  $$+\frac{f(Q_{12})}{(x_2-x_1)(y_2-y_1)}(x_2-x)(y-y_1)+\frac{f(Q_{22})}{(x_2-x_1)(y_2-y_1)}(x-x_1)(y-y_1)$$

  公式看起来有些复杂，我们先来分析一下，因为图像的像素间隔之间都是1，所以$(x_2-x_1)$与$(y_2-y_1)=1$，所以原式变为：
$$f(x,y)=f(Q_{11})(x_2-x)(y_2-y)+f(Q_{21})(x-x_1)(y_2-y)+f(Q_{12})(x_2-x)(y-y_1)+f(Q_{22})(x-x_1)(y-y_1)$$
再由下图可知：

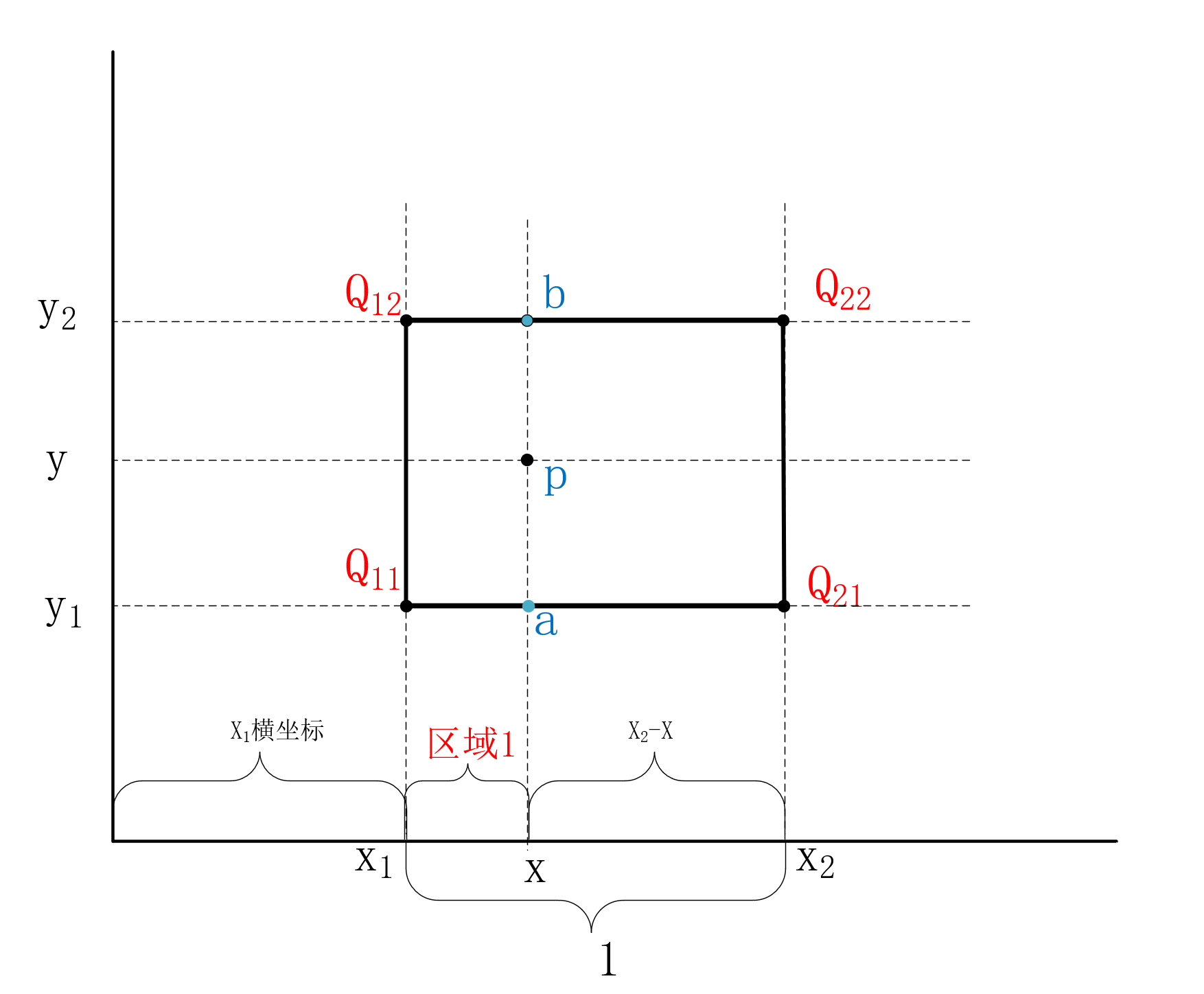
  由上图可以看出，像素点x${}_1$与x${}_2$的距离是1，那么x的坐标只比x${}_1$多零点几，则x的值向下取整 [x] =x${}_1$ 所以区域1的值$=x-[x_1]$记为$u$，所以$x_2-x=1-(x-[x])$为$1-u$。同理$y-[y_1]$记为$v$，所以$y_2-y=1-(y-[y_1])$为$1-v$。
最终图示如下：

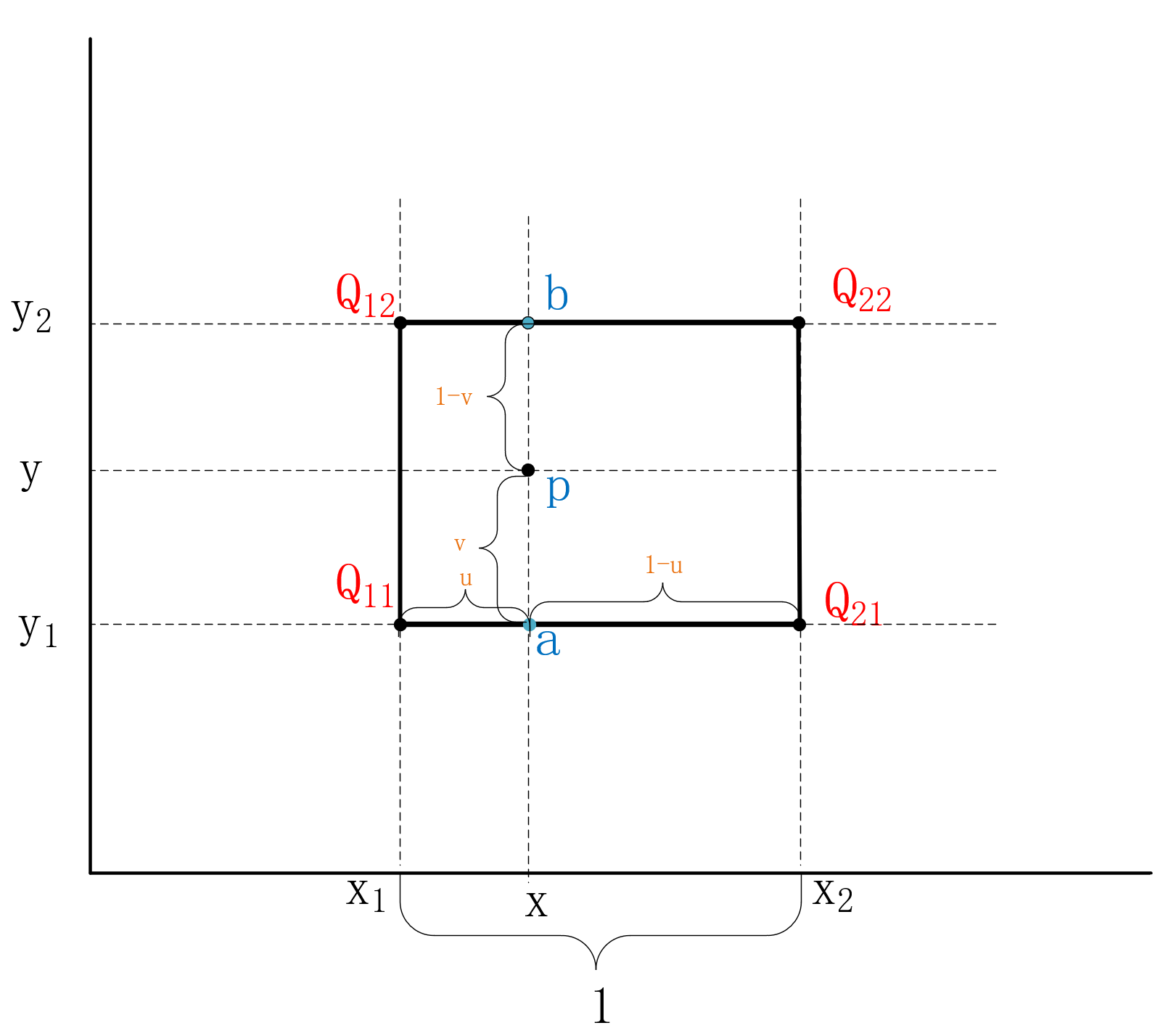
所示公式最终化简为：
$$f(x,y)=f(Q_{11})(1-u)(1-v)+f(Q_{21})u(1-v)+f(Q_{12})(1-u)v+f(Q_{22})uv$$
  这就是双线性插值缩放算法的公式。

三、matlab实现双线性插值算法

1. 首先准备一张图片，我保存了一张分辨率112*103大小的图片
   
   这是我局部截图的QQ图标，保存下来的。
2. 打开matlab，执行对该图片进行双线性缩放，然后看结果，代码如下

% 读取图像
originalImage = imread('C:\Users\Administrator\Desktop\qq.jpg'); % 请替换为您自己的图像文件路径

% 设置缩放因子
scaleFactor = 2.2; % 缩放因子，大于1表示放大，小于1表示缩小

% 使用双线性插值进行图像缩放
scaledImage = imresize(originalImage, scaleFactor, 'bilinear');

% 显示原始图像和缩放后的图像

% 获取图像尺寸
[rows1, cols1, ~] = size(originalImage);

% 设置图像显示的实际大小
figure;
imshow(originalImage, 'InitialMagnification', 'fit'); % 图像自适应窗口大小
axis on; % 显示坐标轴
title('原始图像');

% 设置图像显示的尺寸和分辨率
set(gcf, 'Position', [100, 100, cols1, rows1]); % 设置图像窗口大小
set(gca, 'Units', 'pixels'); % 设置坐标轴单位为像素
set(gca, 'Position', [1080, 1080, cols1, rows1]); % 设置坐标轴位置和大小

% 获取图像尺寸
[rows, cols, ~] = size(scaledImage);

% 设置图像显示的实际大小
figure;
imshow(scaledImage, 'InitialMagnification', 'fit'); % 图像自适应窗口大小
axis on; % 显示坐标轴
title('缩放后的图像');

% 设置图像显示的尺寸和分辨率
set(gcf, 'Position', [100, 100, cols, rows]); % 设置图像窗口大小
set(gca, 'Units', 'pixels'); % 设置坐标轴单位为像素
set(gca, 'Position', [1080, 1080, cols, rows]); % 设置坐标轴位置和大小
 class="hljs-button signin active" data-title="登录复制" data-report-click="{"spm":"1001.2101.3001.4334"}">