因子分析是一种数据简化技术,是一种数据的降维方法。
因子分子可以从原始高维数据中,挖掘出仍然能表现众多原始变量主要信息的低维数据。此低维数据可以通过高斯分布、线性变换、误差扰动生成原始数据。
因子分析基于一种概率模型,使用EM算法来估计参数。
主成分分析(PCA)也是一种特征降维的方法。
学习理论中,特征选择是要剔除与标签无关的特征,比如“汽车的颜色”与“汽车的速度”无关;
PCA中要处理与标签有关、但是存在噪声或者冗余的特征,比如在一个汽车样本中,“千米/小时”与“英里/小时”中有一个冗余了。
PCA的方法比较直接,只要计算特征向量就可以降维了。
独立成分分析(ICA)是一种主元分解的方法。
其基本思想是从一组混合的观测信号中分离出独立信号。比如在一个大房间里,很多人同时在说话,样本是这个房间里各个位置的一段录音,ICA可以从这些混合的录音中分离出每个人独立的说话的声音。
ICA认为观测信号是若干个统计独立的分量的线性组合,ICA要做的是一个解混过程。
因为因子分析、PCA、ICA都是对数据的处理方法,就放在这同一份总结里了。
1、因子分析(Factor analysis)
1.1、因子分析的直观理解
因子分析认为高维样本点实际上是由低维样本点经过高斯分布、线性变换、误差扰动生成的。让我们来看一个简单例子,对低维数据如何生成高维数据有一个直观理解。
假设我们有m=5个2维原始样本点如下:
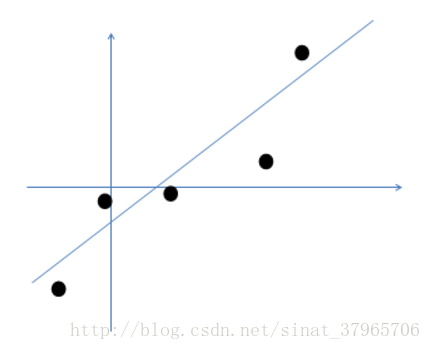
图一
那么按照因子分析的做法,原始数据可以由以下过程生成:
①在一个低维空间(此处是1维)中,存在着由高斯分布生成的m

图二
②使用某个 Λ=(a,bT)
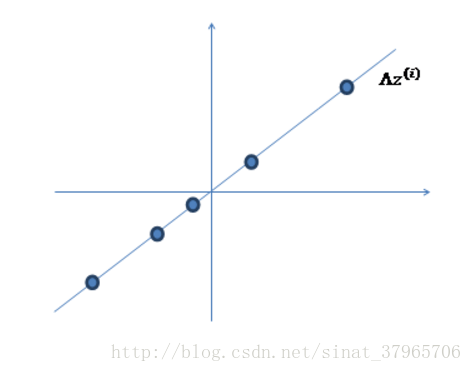
图三
③加上 μ(μ1,μ2)T,让直线过 μ——实际上是将样本点横坐标加 μ1,纵坐标加 μ2:
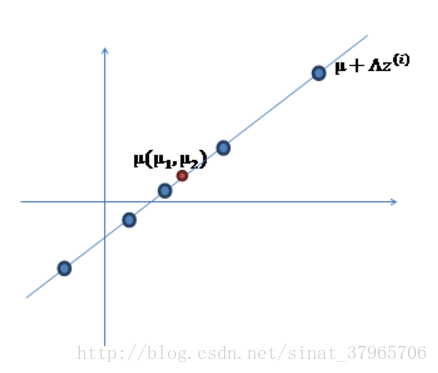
图四
④对直线上的点做一定的扰动,其扰动为 ε~ N(0,ψ):

图五
黑点就是图一中的原始数据。
1.2、因子分析的一般过程
因子分析认为m个n维特征的训练样例(x(1),x(2),⋯,x(m))的产生过程如下:
①在一个k维空间中,按照多元高斯分布生成m个z(i)(k维向量,k<n),即
z(i)~N(0,I)
②存在一个变换矩阵Λ∈Rn∗k,将z(i)映射到n维空间中,即
Λz(i)
③将Λz(i)(n维)加上一个均值μ(n维),即
μ+Λz(i)
④对每个点加上符合多元高斯分布的扰动ε~N(0,ψ)(n维向量),即
x(i)=μ+Λz(i)+ε
1.3、因子分析模型
模型与参数概述
由上面的分析,我们定义因子分析的模型为:
ε~ N(0,ψ)
x=μ+Λz+ε
其中 z和 ε是相互独立的。并且由上面的分析过程,我们可以直观地感受到我们的 参数是μ∈Rn、Λ∈Rn∗k、ψ∈Rn∗n。
另一个等价的假设是,(x,z)联合分布如下,其中z∈Rk是一个隐藏随机变量:
这个假设会在使用EM算法求解因子分析参数,E步中迭代 Q分布的时候用到。
接下来的课程,是使用高斯模型的矩阵表示法来对模型进行分析。矩阵表示法认为z与 x 联合符合多元高斯分布,即:
多元高斯分布的原始模型是:
其中 x是 k维向量, μ是 k维向量, Σ是 k∗k协方差矩阵。
很明显在多元高斯分布模型下,参数是 μzx,Σ——它们是由 x,z的联合分布生成的,所以我们可以用我们的原始参数 μ,Λ,ψ来表示 μzx,Σ,求得 x的边缘分布,再把相关参数带入式(3),这就得到了关于我们参数的概率分布,然后就可以通过最大似然估计来求取我们的参数。
求取μzx μzx是x,z联合分布的期望值(期望的定义:所有结果*相应概率的总和):
μzx=E[zx]=[E(z)E(x)] 由z~N(0,I)我们可以简单获得E(z)=0。
类似地由ε~N(0,ψ),x=μ+Λz+ε,μ是一个常数,我们有:
E[x]=E[μ+Λz+ε]=E[μ]+ΛE[z]+E[ε]=μ+0+0=μ
所以:
μzx=[→0μ] 求取Σ
Σ是x,z联合分布的协方差矩阵。
方差,度量随机变量与期望之间的偏离程度,定义如下:
Var(X)=E((X−E(X))2)=E(X2)−(E(X)2)
协方差,两个变量总体误差的期望,定义如下:
Cov(X,Y)=E((X−E(X))(Y−E(Y)))
协方差、方差、期望之间的一些相互关系如下:
Cov(X,X)=Cov(X)=Var(X)=E(XXT)=σ2 下面开始求取Σ。
Σ=Cov[zx]=[ΣzzΣzxΣxzΣxx]=E[(z−E(z))(z−E(z))T(z−E(z))(x−E(x))T(x−E(x))(z−E(z))T(x−E(x))(x−E(x))T] 由z~N(0,I),可以简单得到:
Σzz=Cov(z)=σ2=I
由 ε ~ N(0,ψ) , x=μ+Λz+ε , E(x)=μ ,并且 z 和ε是相互独立,有:
Σzx=E[(z−E(z))(x−E(x))T]=E[(z−0)(μ+Λz+ε−μ)T]=E[zzT]ΛT+E[zεT]=IΛT+0=ΛT
类似地,我们可以得到:
Σxx=E[(x−E(x))(x−E(x))T]=E[(μ+Λz+ε−μ)(μ+Λz+ε−μ)T]=ΛE[zzT]ΛT+E[εεT]=ΛIΛT+ψ=ΛΛT+ψ 用最大似然估计法求解参数
经过上面的步骤,我们就把μzx,Σ用我们的参数μ,Λ,ψ表示出来了:
[zx]
~
N(μzx,Σ)
~
N([→0μ],[IΛTΛΛΛT+ψ])
然后我们可以求得 x 的边缘分布:
x
~
N(μ,ΛΛT+ψ)
因此,给定一个训练集
{x(i);i=1,2,⋯,m}
,把参数带入式(3),我们可以写出下面的似然函数:
类似地由ε~N(0,ψ),x=μ+Λz+ε,μ是一个常数,我们有:
方差,度量随机变量与期望之间的偏离程度,定义如下:
因此,给定一个训练集 {x(i);i=1,2,⋯,m} ,把参数带入式(3),我们可以写出下面的似然函数:

评论记录:
回复评论: