一、核心思想
区别于普通神经网络,循环神经网络Recurrent neural network (RNN)不仅仅单独的取处理一个个的输入,前一个输入和后一个输入不是完全没有关系的。在某些任务中,需要能够更好的处理序列的信息,即前面的输入和后面的输入是有关系的。
二、结构
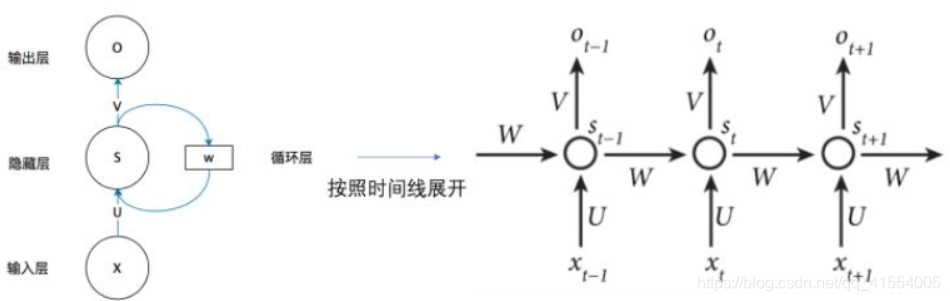
最简单的循环神经网络由输入层、一个隐藏层和一个输出层组成:
O
t
=
f
o
(
V
∗
S
+
b
o
)
S
t
=
f
s
(
U
∗
X
t
+
W
∗
S
t
−
1
+
b
s
)
O_t = f_o(V*S+b_o)\\ S_t = f_s(U*X_t+W*S_{t-1}+b_s)
Ot=fo(V∗S+bo)St=fs(U∗Xt+W∗St−1+bs)
如果把上面左图有
W
W
W的那个带箭头的圈去掉,它就变成了最普通的全连接神经网络。
X X X是输入向量,表示输入的值
S S S是状态向量,表示隐藏层的值(这里隐藏层面画了一个节点,但可以想象这一层其实是多个节点,节点数与向量 S S S的维度相同,同时也可以有很多层)
O O O是输出向量,表示输出层的值
U U U是输入层到隐藏层的权重矩阵
V是隐藏层到输出层的权重矩阵
W W W是状态之间传递的权重矩阵
f o , b o , f s , b s f_o,b_o,f_s,b_s fo,bo,fs,bs都是对应的激活函数和偏移
达到的效果:就是循环神经网络的隐藏层的状态 S t S_{t} St不仅仅取决于当前这次的输入 X t X_{t} Xt,还取决于上一次隐藏层的值 S t − 1 S_{t-1} St−1。
三、为什么需要反馈?
卷积神经网络(CNN)更关注局部特征的提取,大部分情况下也确实是卷积网络比递归网络和循环网络更容易引领state-of-arts。然而,还有一些任务的labels之间会有很强的相关性。
举个例子,当有依据较长的句子时,CNN如果需要理解这句话的意思时,就需要有一定长的的滤波器长度才有较大的可能性正确标注这个句子的labels。而对更长的输入类似于文章,那代价就会更大,无限增长滤波器的长度是不现实的。所以想法就是让模型在当前位置的输出再反馈给模型,来帮助模型做下一位置的决策!
这样的有反馈单元的模型在做当前位置的决策的时候,会同时考虑前面所有位置/时间点的情况(直接考虑上一时间点,又由于上一时间点也考虑了上上时间点,因此间接考虑了上一时间点前面所有的时间点),从而可以最大可能的完成正确决策。
相比之下,在卷积网络中,由于它视野有限,不瞻前顾后,所以它更可能觉得短时间内(滤波器长度范围可见范围内出现)的这种情况应该做出某种决策,但是实际上判断出现了问题,因为在训练集中可能有了基于更长时间尺度更宽滤波器可见范围内的诠释或规律。
四、RNN的问题
首先,从单个的RNN节点前向过程看,可以认为它只有一次权重矩阵 W W W(可以是很多层去拟合不同时间之间的传递关系,但我们将他概括为一个传递矩阵矩阵)(另外先不管 V V V)。由此可见从长时间的序列的角度去看RNN的前向过程,就可以认为RNN是一个通过多个相同传递矩阵相连接的深层网络。忽略 V V V和激活函数后,就可以近似的认为网络一共有 T T T层( T T T等于序列的长度),那么第 t t t层的输出就是输入连续经过 t t t次权重 W W W的权重相乘(当然同时里面还有激活只不过我们先不考量),也就是 W t W^t Wt!
矩阵论中得知,矩阵可以用它的特征值矩阵和特征向量矩阵去近似,即
W
≈
V
d
i
a
g
(
λ
)
V
−
1
W
t
=
{
V
d
i
a
g
(
λ
)
V
−
1
}
t
=
V
d
i
a
g
(
λ
)
t
V
−
1
W ≈ Vdiag(λ)V^{-1}\\ W^t = \{Vdiag(λ)V^{-1}\}^t = Vdiag(λ)^tV^{-1}
W≈Vdiag(λ)V−1Wt={Vdiag(λ)V−1}t=Vdiag(λ)tV−1
**特征值矩阵中的每个特征值对结果的影响都会随着t的增大发生指数级变化!**所以某个特征值大于1时,就容易导致这个序列初始的输入和状态会对之后的状态有很大的影响(指数级别增长);当特征值小于1时,会就会这个序列初始的输入和状态会对之后的状态有很小的影响(指数级别衰减到0)。
就前向过程看是如此,同时就误差反向传播的过程也是如此。即使近输出层与label的误差很小,但是计算倒数 t t t层的梯度时,会乘以 W t W^t Wt来得到,然而由于刚才讲的由序列长度所带来的影响不是随着 t t t指数级减小就是随着 t t t指数级增长。所以当更新RNN的靠前的层的时候(即离着输出层较远的那些层,或者说与序列末端离得远的位置的权重梯度时候),计算出的梯度要么非常大,要么小的忽略。小的可以忽略的梯度不会对 W W W的更新有任何指导作用,大的值更新步长过大,就会把 W W W中的某些值更新过度,很难达到局部最优。这个现象叫做梯度消失和梯度爆炸。
五、解决方法呢?
简单的想法是进行梯度截断,在优化RNN的参数的时候,给剃度值设置一个上限,免得发生爆炸摧毁我们之前积累的结果。但是这样显然就会导致模型难以再顾及很靠前的历史信息了(梯度都被大幅阉割或者自己消失了),因此理论上RNN可以保存任意长的历史信息来辅助当前时间点的决策,然而由于在优化时(训练RNN时),梯度无法准确合理的传到很靠前的时间点,因此RNN实际上只能记住并不长的序列信息(在NLP中,经验上认为序列大于30的时候,RNN基本记不住多于30的部分,而从多于10的位置开始就变得记性很差了),因此RNN相比一般前馈网络,可以记住的历史信息要长一些,但是无法记住长距离的信息(比如段落级的序列甚至篇章级的序列,用RNN就鸡肋了)。
使用梯度截断的trick可以减轻参数矩阵连乘带来的问题。如前所述,由于前向过程也会对参数矩阵进行连乘,显然乘的次数多了,就会容易产生很大的值(包括很大的正值与很小的负值),这是矩阵相乘的结果就会趋近于很大的或者很小,从而进入激活函数的计算,在反向传播时会因为激活函数出现一些问题。
对于sigmoid的导数
σ
′
(
z
)
=
σ
(
z
)
(
1
−
σ
(
z
)
)
σ′(z) = σ(z)(1-σ(z))
σ′(z)=σ(z)(1−σ(z))
来说,显然无论输入的z是超大正值也好,超小负值也好,都会导致其导数接近0!因此直接导致梯度传到这里后就消失了!而ELU 的导数和ReLU的导数则不会有这个问题。因此在RNN中,更要注意一般情况下不要使用sigmoid作为激活函数。
六、总结
RNN的想法很简单,直接引入了反馈单元来记忆历史信息。然而由于训练时的梯度爆炸与消失,导致其难以学习远距离历史信息(或者说与当前时间点的远距离依赖关系),因此要注意使用梯度截断的trick来处理优化过程,同时要避开sigmoid这类容易带来梯度饱和的激活函数。

评论记录:
回复评论: