推荐|详解欧拉角与四元数

一、欧拉角

1.1 静态的定义

对于在三维空间里的一个参考系，任何坐标系的取向，都可以用三个欧拉角来表现。参考系又称为实验室参考系，是静止不动的。而坐标系则固定于刚体，随着刚体的旋转而旋转。

如图所示。设定xyz-轴为参考系的参考轴。称xy-平面与XY-平面的相交为交点线，用英文字母（N）代表。zxz顺规的欧拉角可以静态地这样定义：

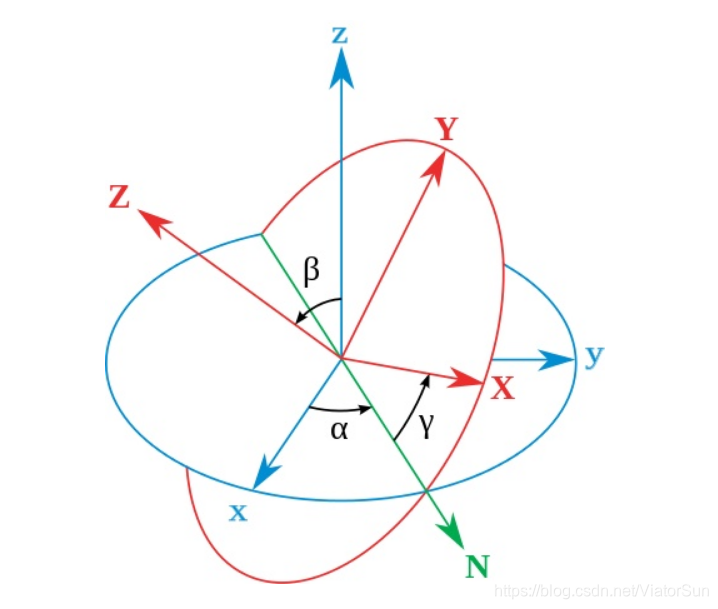
在这里插入图片描述

$\alpha$ 是 x-轴与交点线的夹角，
$\beta$ 是z-轴与Z-轴的夹角，
$\gamma$ 是交点线与X-轴的夹角。

很可惜地，对于夹角的顺序和标记，夹角的两个轴的指定，并没有任何常规。科学家对此从未达成共识。每当用到欧拉角时，我们必须明确的表示出夹角的顺序，指定其参考轴。

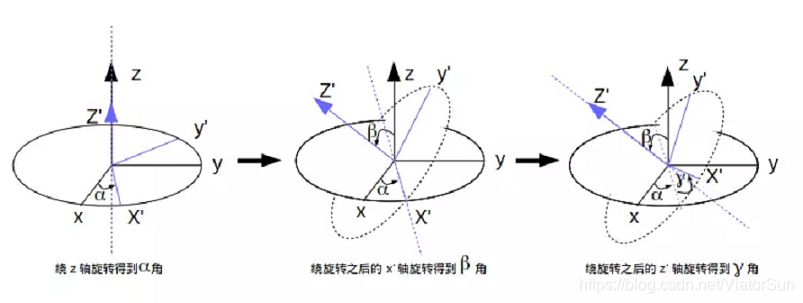
下面我们通过图例来看看欧拉角是如何产生的，并且分别对应哪个角度。

1.2 欧拉角的表示

在这里插入图片描述

1.3 作用

欧拉角Eulerian angles用来确定定点转动刚体位置的3个一组独立角参量，由章动角 θ、旋进角（即进动角）ψ和自转角j组成。

欧拉角包括3个旋转，根据这3个旋转来指定一个刚体的朝向。这3个旋转分别绕x轴，y轴和z轴，分别称为 Roll（翻滚），Pitch（俯仰）和 Yow（偏航），如下图所示。旋转的遵循右手坐标系，欧拉角可以表示成z-x-z，x-y-x，z-y-z等形式，旋转的顺序影响结果。

欧拉角

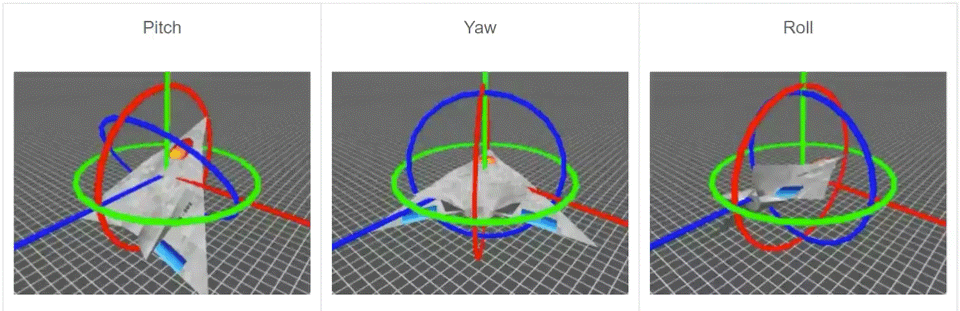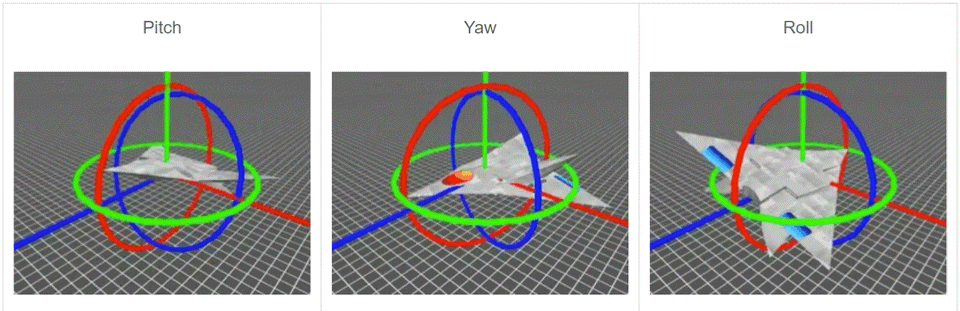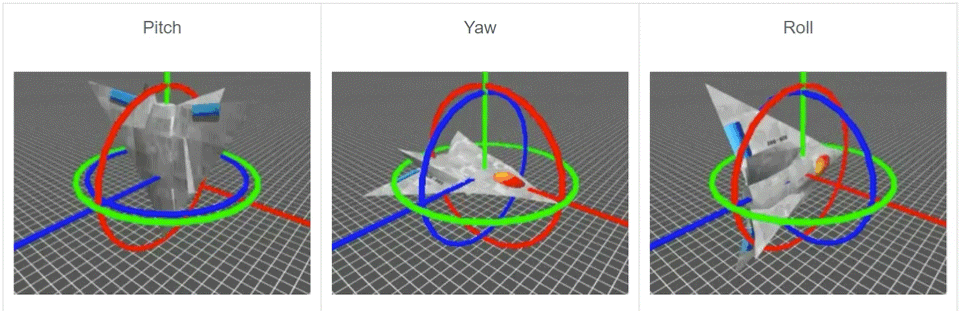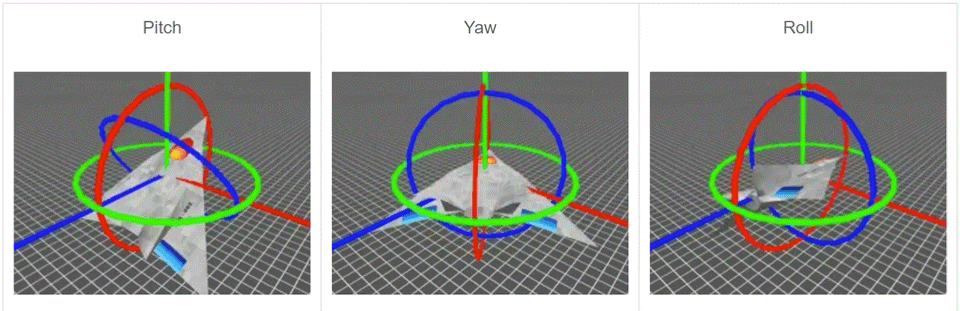
欧拉角很重要的一个优点就是直观，容易理解。

欧拉角的优缺点

优点：

三个角度组成，直观，容易理解。
可以进行从一个方向到另一个方向旋转大于180度的角度。

缺点：

欧拉角是不可传递的，旋转的顺序影响旋转的结果，不同的应用又可能使用不同的旋转顺序，旋转顺序无法统一；
3个旋转的角度可以不受限制，即可以是10000度，也可以是-1500度；
可能造成万向节死锁（Gimbal Lock）

1.4 万向锁问题

对于动态欧拉角，即绕物体坐标系旋转。（静态不存在万向锁的问题）无论heading和bank为多少度，只要pitch为±90°（即绕第二个轴的旋转），就会出现万向锁现象。

为了对这一现象有一个感性的认识，请拿起自己的手机（没有？不会吧）和一支笔（用作旋转轴），
亲手做如下的几个旋转。

首先确定手机的物体坐标系朝向，为了方便记忆，我们假设z轴与手机屏幕垂直（手机平放于桌面）指向上方，手机较短的一条边为x轴，较长的一条边为y轴（方向由手机尾部指向头部），物体坐标系的原点是手机左下角的顶点。（注意旋转顺序为zyx）绕z轴旋转任意角度（注意x和y轴也跟着一起旋转），再绕y轴旋转90°，再绕x轴旋转任意角度。通过多次尝试，你会发现一个共同点：z轴永远是水平的，通俗的说，手机永远也不会立起来！本来我们以为手机会指向任何方向，但实际上手机好像是被锁在桌面上，只能指向水平的某个方向，这个现象就称为万向锁。而如果绕y轴旋转不等于90°（1°也好89°也好），只要选择适当的绕x和z的角度，就可以让手机指向三维空间中的任何一个方向，手机是自由的，也就不会遇到万向锁现象。

万向锁的避免问题：限制旋转的角度范围

heading-pitch-bank
heading 绕Y轴限制范围在±180°
pitch 绕X轴限制范围在±90°
bank 绕Z轴

二、四元数

什么是四元数？

在计算机图形学中，四元数用于物体的旋转，是一种较为复杂，但是效率较高的旋转方式。在三种坐标变换：旋转，平移，缩放当中，旋转应该算是比较复杂的存在。平常我们接触的比较多的是矩阵变换和欧拉变换。对于一个物体的旋转，其实我们只需要知道四个值：一个旋转的向量 + 一个旋转的角度。而四元数也正是这样的设计：

其中x,y,z 代表的是向量的三维坐标，w代表的是角度；同时我们也可以写成以下的形式方便我们计算和分析： $q = (x, y, z, w)$

其实，四元数本质上是一个超复数， $\space \space \space, \space \space \space i^2 = j^ 2 = k^2 = -1$

$\begin{bmatrix} \vec{v} & w \end{bmatrix}$

四元数的优缺点

内部由四个数字（在Unity中称为x，y，z和w）组成，然而这些数字不表示角度或轴，并且通常不需要直接访问它们。除非你特别有兴趣深入了解四元数学，你只需要知道四元数表示三维空间中的旋转，你通常不需要知道或修改x，y和z属性。

优点：

存储空间小，计算效率高。
四元旋转不存在万向节锁问题。

缺点：

四元数的数字表示不直观。
单个四元数不能表示在任何方向上超过180度的旋转。

参考链接

https://www.jianshu.com/p/21ab3e1d3422
http://mini.eastday.com/mobile/180306210610472.html
https://blog.csdn.net/wwlcsdn000/article/details/79421612