一、下载QEMU
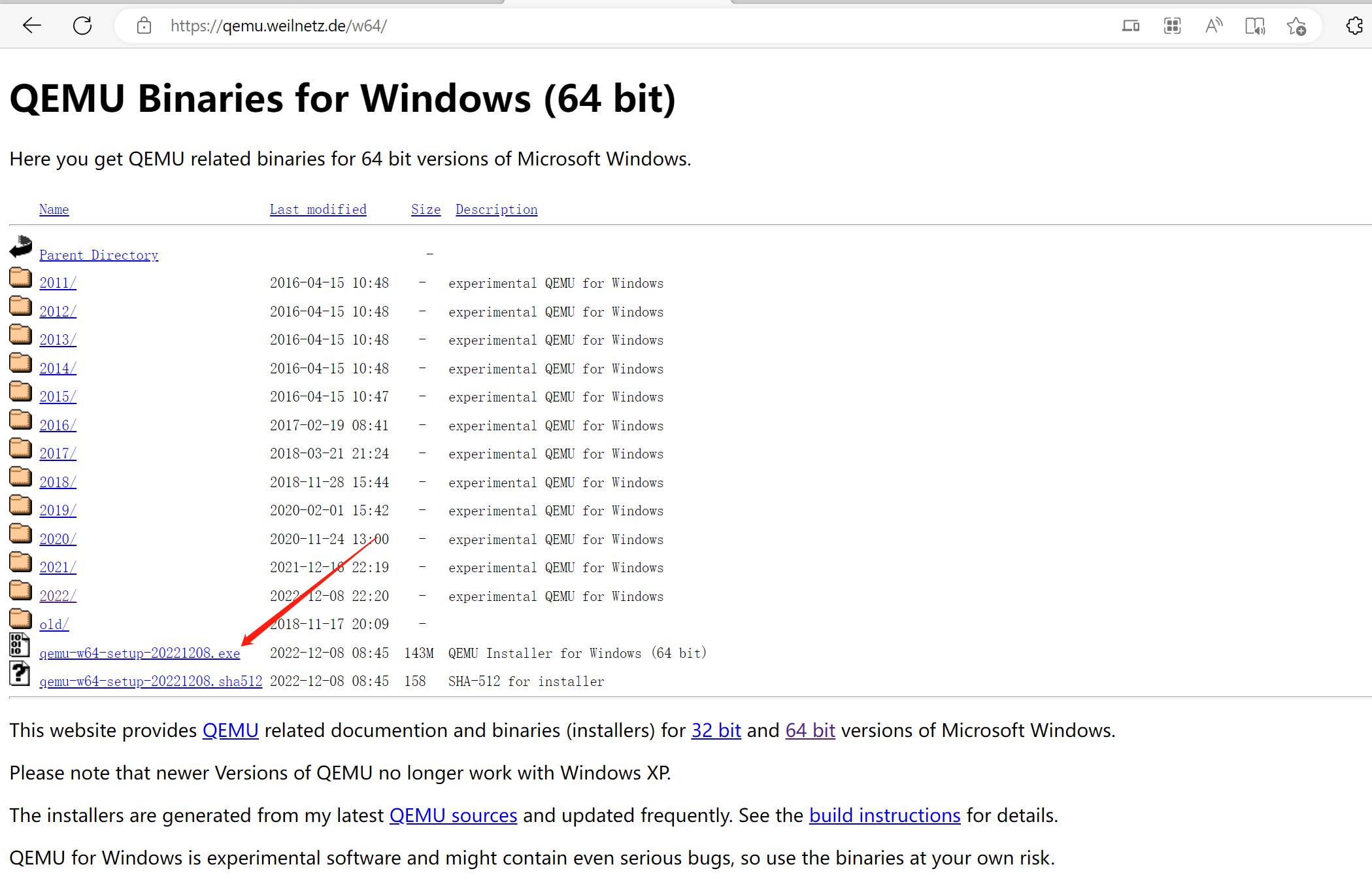
二、下载 QEMU UEFI 固件文件
https://releases.linaro.org/components/kernel/uefi-linaro/latest/release/qemu64/QEMU_EFI.fd
这里下载的是16.02的版本,放在了 F:\QEMU 根目录。
网上还能找到一些其它版本,但是推荐使用这个,兼容性比较好。
三、aarch64 的光盘镜像文件
openEuer官网镜像下载:https://www.openeuler.org/zh/download/

本文使用的是一个 openEuler-20.03-LTS-SP3 镜像文件。
https://mirrors.tuna.tsinghua.edu.cn/openeuler/openEuler-20.03-LTS-SP3/ISO/aarch64/openEuler-20.03-LTS-SP3-aarch64-dvd.iso
四、安装设置 QEMU
QEMU下载好后,直接双击安装,路径根据自身喜好选择即可。
这里是安装在默认路径:D:\Program Files\qemu
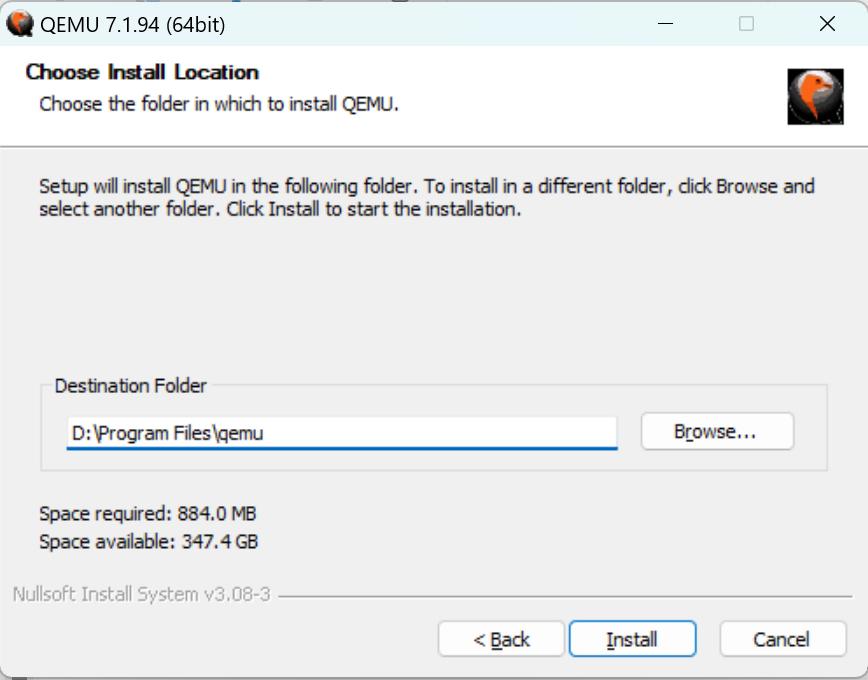
安装完成后,在Path环境变量中添加QEMU路径
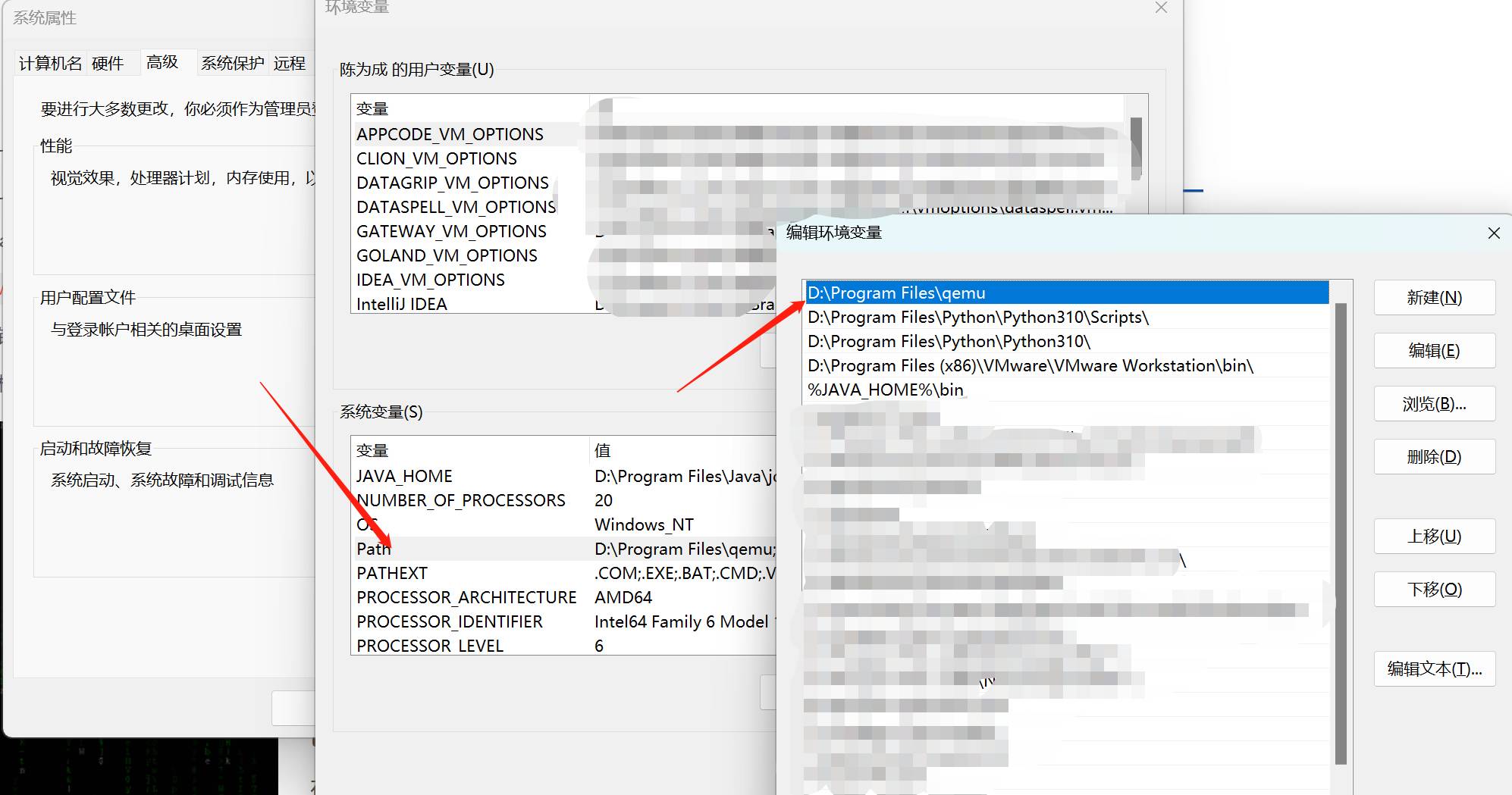
五、创建虚拟网卡
1、安装 tap-windows
下载地址:https://build.openvpn.net/downloads/releases/
Win10版本的:https://build.openvpn.net/downloads/releases/tap-windows-9.24.7-I601-Win10.exe
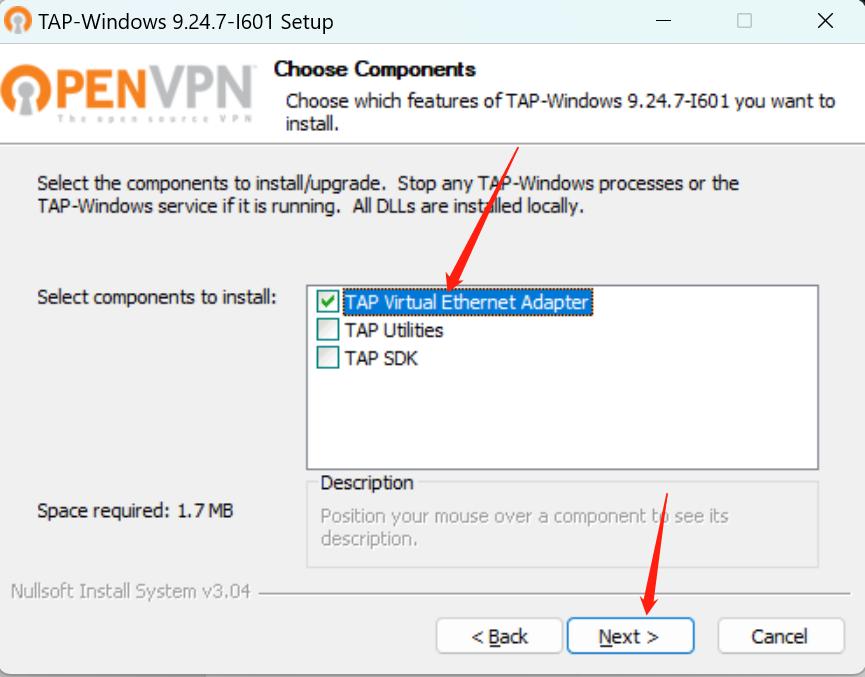
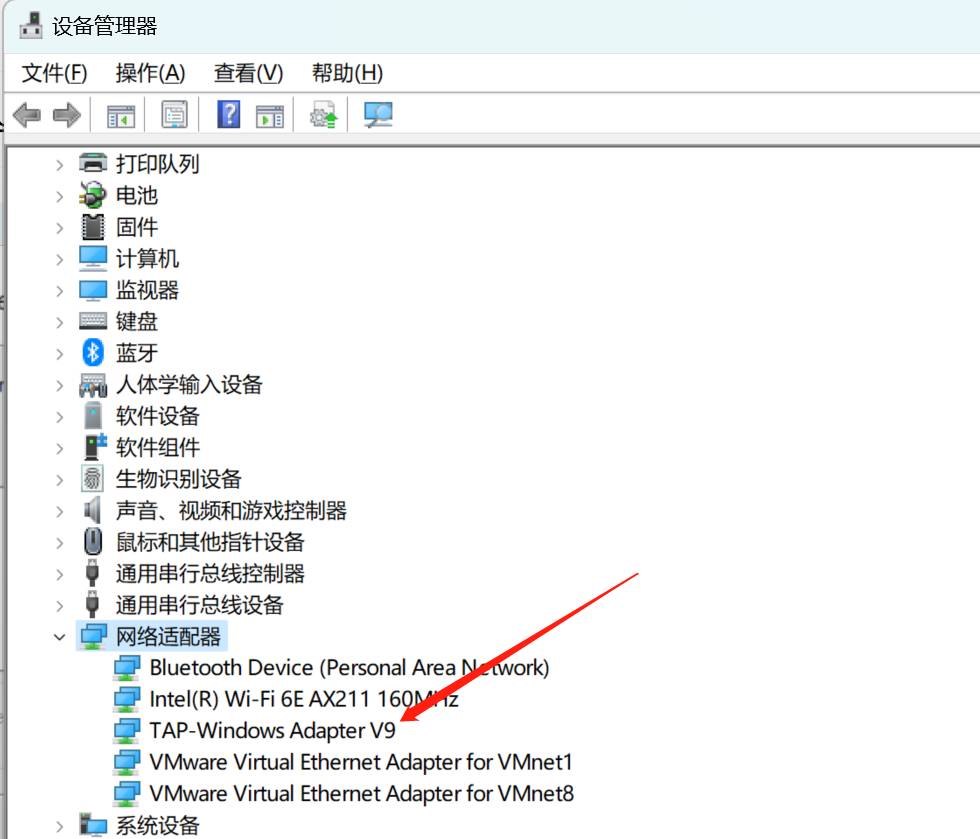
2、重命名新网卡
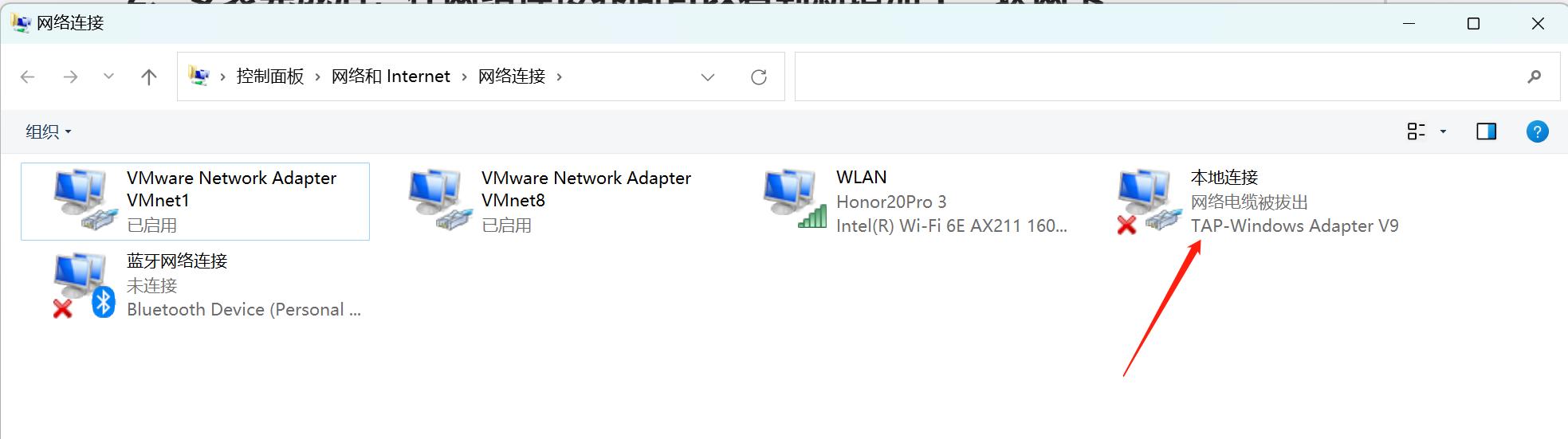
右键单击新增加的网卡,重命名该网卡
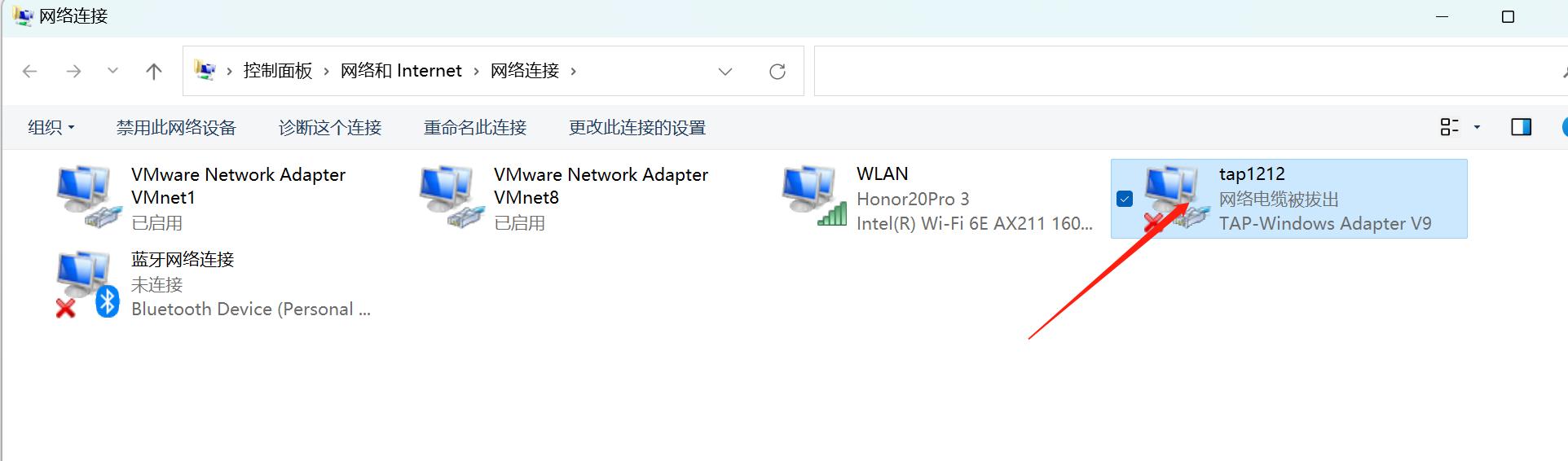
3、共享物理网卡的网络
右键单击本机物理网卡,点击“属性”按钮,在弹出的界面中选择“共享”选项
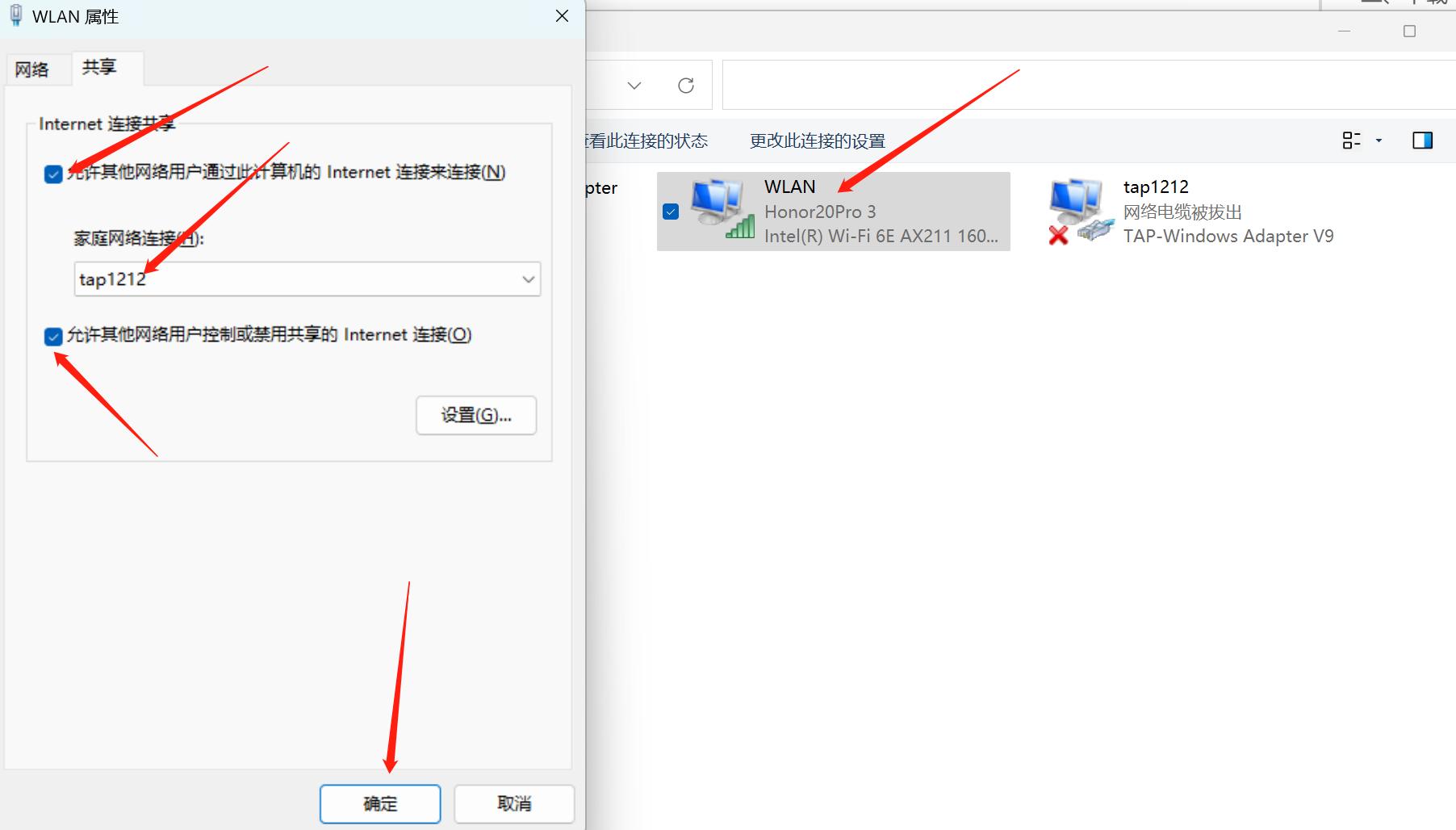
选中“允许其它网络通过此计算机的Internet连接来连接”复选框,“家庭网络连接”项选择刚才新增加的网卡(且是修改过名字后的名称),选中“允许其它网络用户控制或禁用共享的Internet连接”,确定即可。
六、创建硬盘镜像
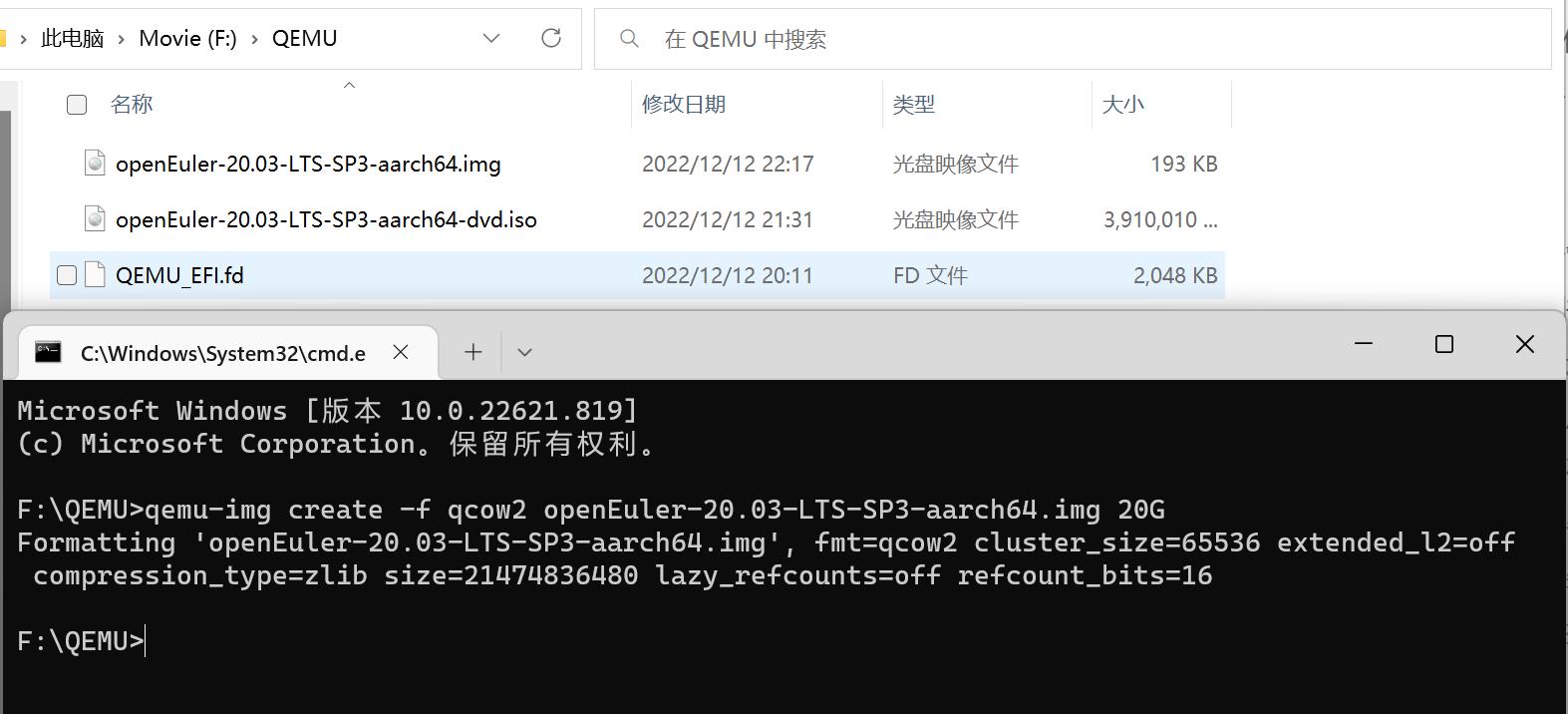
在 PowerShell 或者 CMD 中输入
qemu-img create -f qcow2 openEuler-20.03-LTS-SP3-aarch64.img 20G
- 1
指定硬盘镜像名,大小为 20G
七、安装镜像
qemu-system-aarch64 -m 4000 -cpu cortex-a72 -smp 4,cores=4,threads=1,sockets=1 -M virt -bios F:\QEMU\QEMU_EFI.fd -net nic -net tap,ifname=tap1212 -device nec-usb-xhci -device usb-kbd -device usb-mouse -device VGA -drive if=none,file=F:\QEMU\openEuler-20.03-LTS-SP3-aarch64-dvd.iso,id=cdrom,media=cdrom -device virtio-scsi-device -device scsi-cd,drive=cdrom -drive if=none,file=F:\QEMU\openEuler-20.03-LTS-SP3-aarch64.img,id=hd0 -device virtio-blk-device,drive=hd0
- 1
- -m 4000 表示分配给虚拟机的内存最大4000MB,可以直接使用 -m 4G
- -cpu cortex-a72 指定CPU类型,还可以选择cortex-a53、cortex-a57等
- -smp 4,cores=4,threads=1,sockets=1 指定虚拟机最大使用的CPU核心数等
- -M virt 指定虚拟机类型为virt,具体支持的类型可以使用 qemu-system-aarch64 -M help 查看
- -bios F:\QEMU\QEMU_EFI.fd 指定UEFI固件文件
- -net tap,ifname=tap1212 启用网络功能(ifname=tap1212中的tap1212请修改为前面步骤中自己修改后的网卡名称)
- -device nec-usb-xhci -device usb-kbd -device usb-mouse 启用USB鼠标等设备
- -device VGA 启用VGA视图,对于图形化的Linux这条很重要!
- -drive if=none,file=F:\QEMU\openEuler-20.03-LTS-SP3-aarch64-dvd.iso,id=cdrom,media=cdrom 指定光驱使用镜像文件
- -device virtio-scsi-device -device scsi-cd,drive=cdrom 指定光驱硬件类型
- -drive if=none,file=F:\QEMU\openEuler-20.03-LTS-SP3-aarch64.img 指定硬盘镜像文件
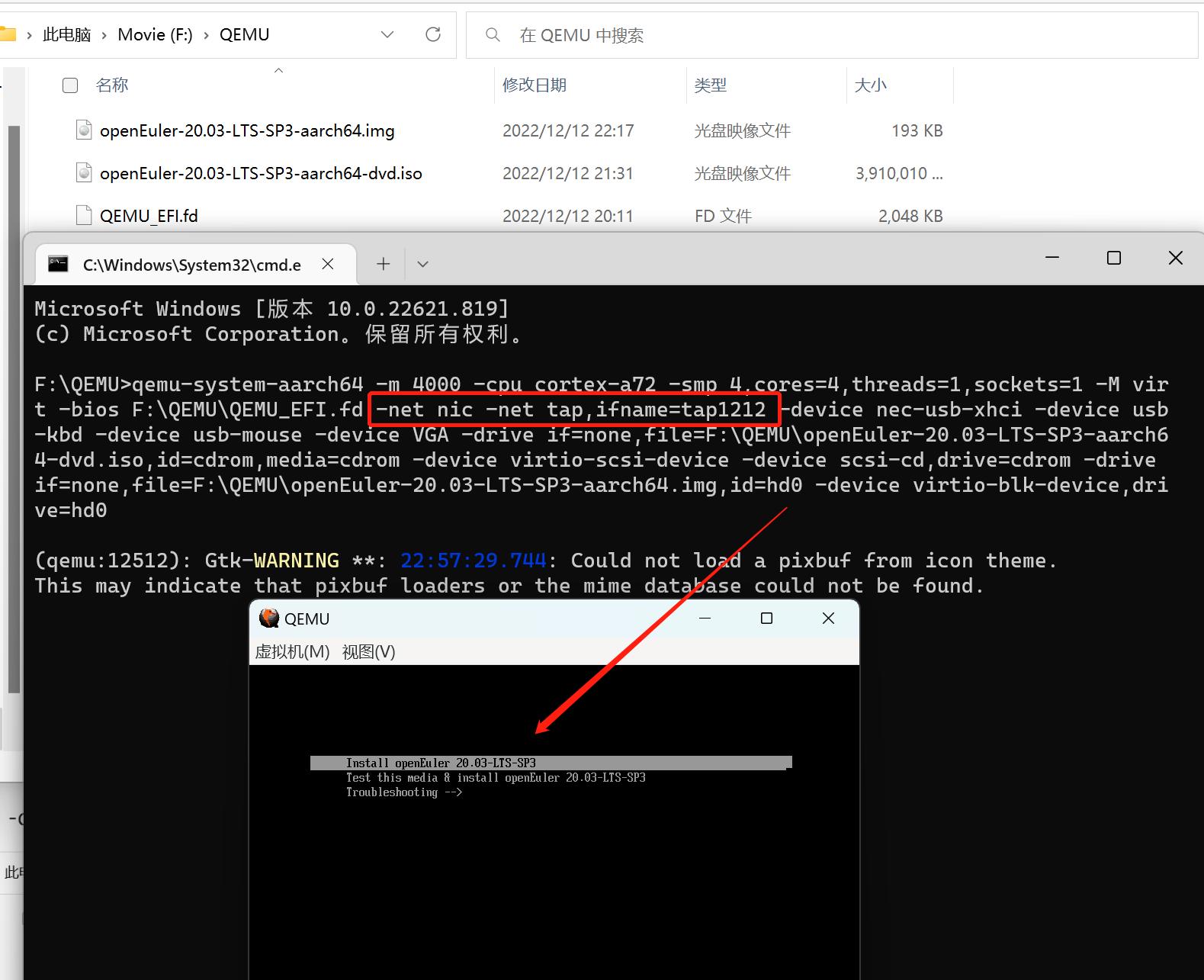
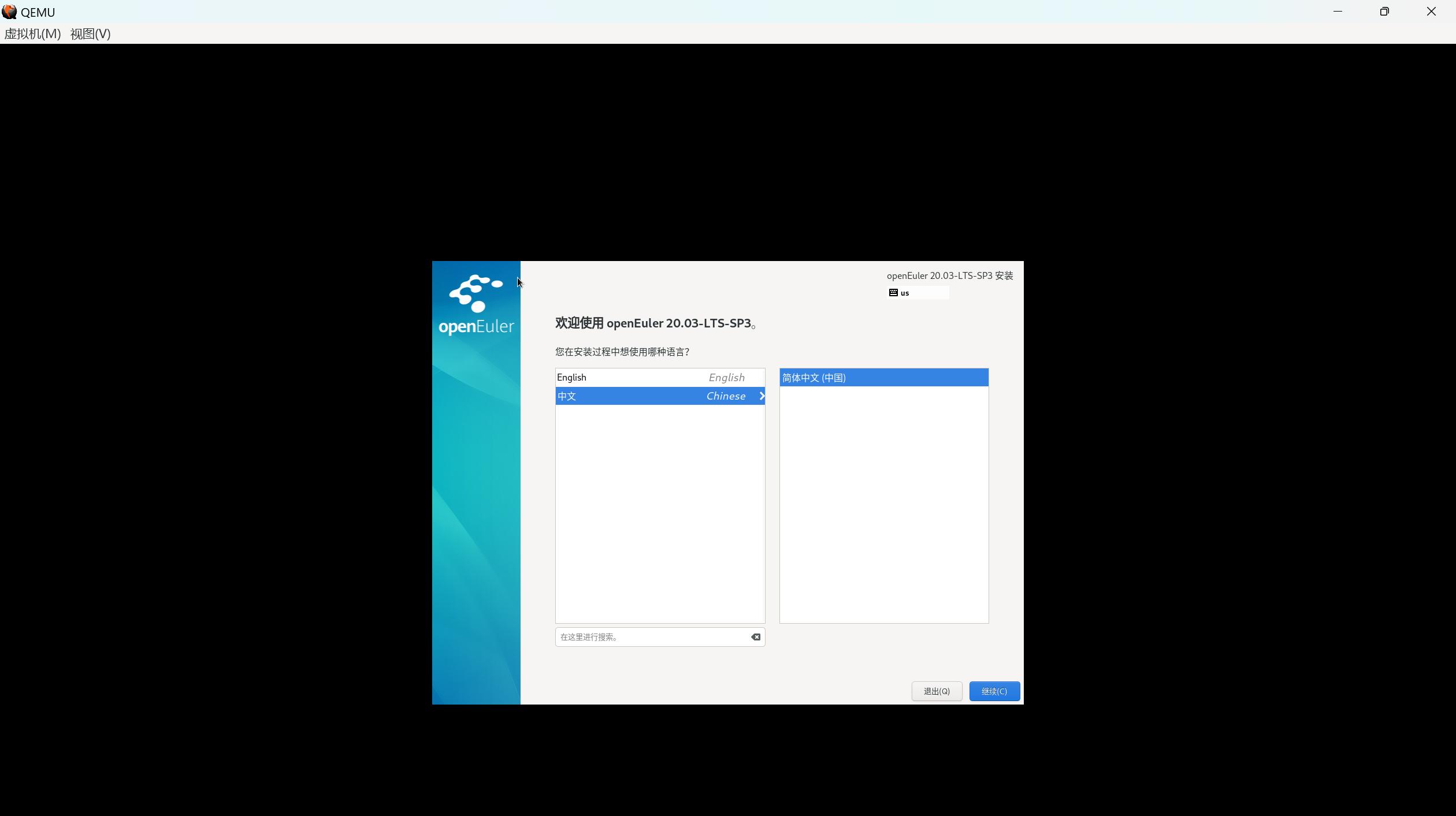
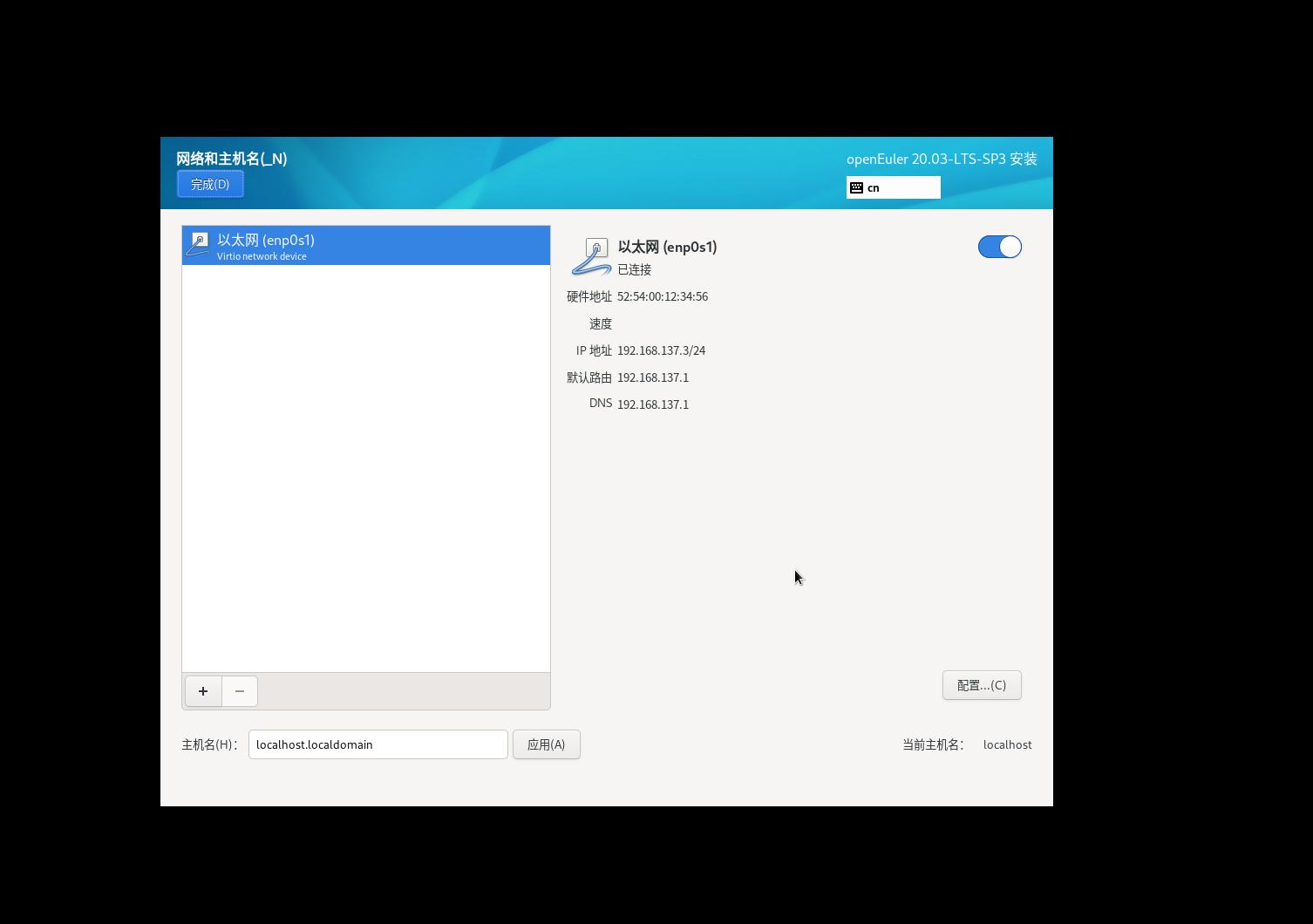
只有上面创建了虚拟网卡,这里才会有网卡显示(注意,手动配置网络的时候网关不能配置错误,否则虚拟机连不上外网)
安装非常慢!!!!一般半小时起步!!!!!!!
八、启动镜像
qemu-system-aarch64 -m 4000 -cpu cortex-a72 -smp 4,cores=4,threads=1,sockets=1 -M virt -bios F:\QEMU\QEMU_EFI.fd -net nic -net tap,ifname=tap1212 -device nec-usb-xhci -device usb-kbd -device usb-mouse -device VGA -drive if=none,file=F:\QEMU\openEuler-20.03-LTS-SP3-aarch64.img,id=hd0 -device virtio-blk-device,drive=hd0
- 1
九、连接 ssh
登录后启用网卡
cd /etc/sysconfig/network-scripts/
vi ifcfg-enp0s1
- 1
- 2
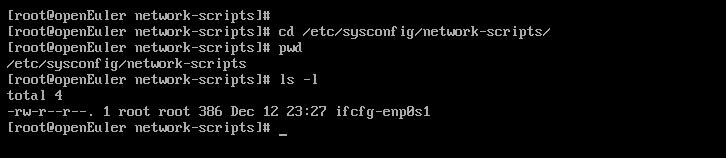
ONBOOT改为yes,保存退出
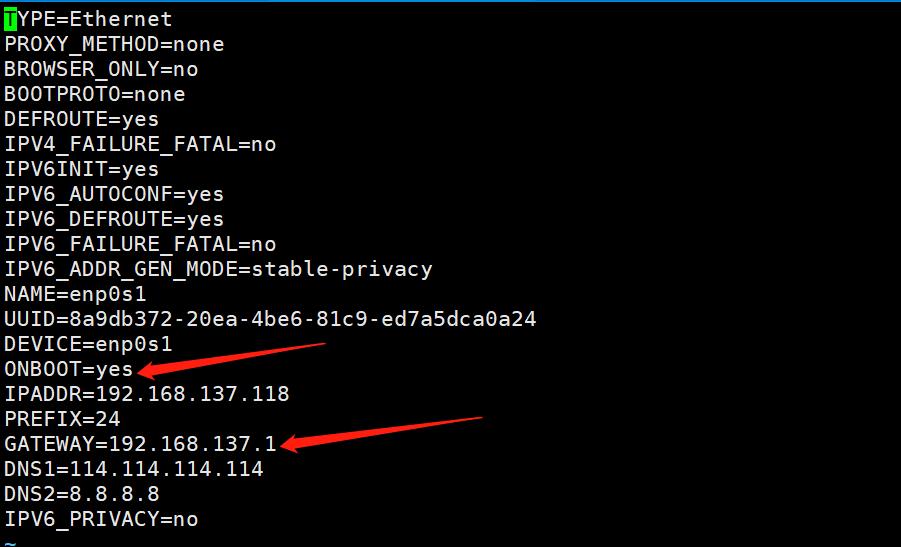
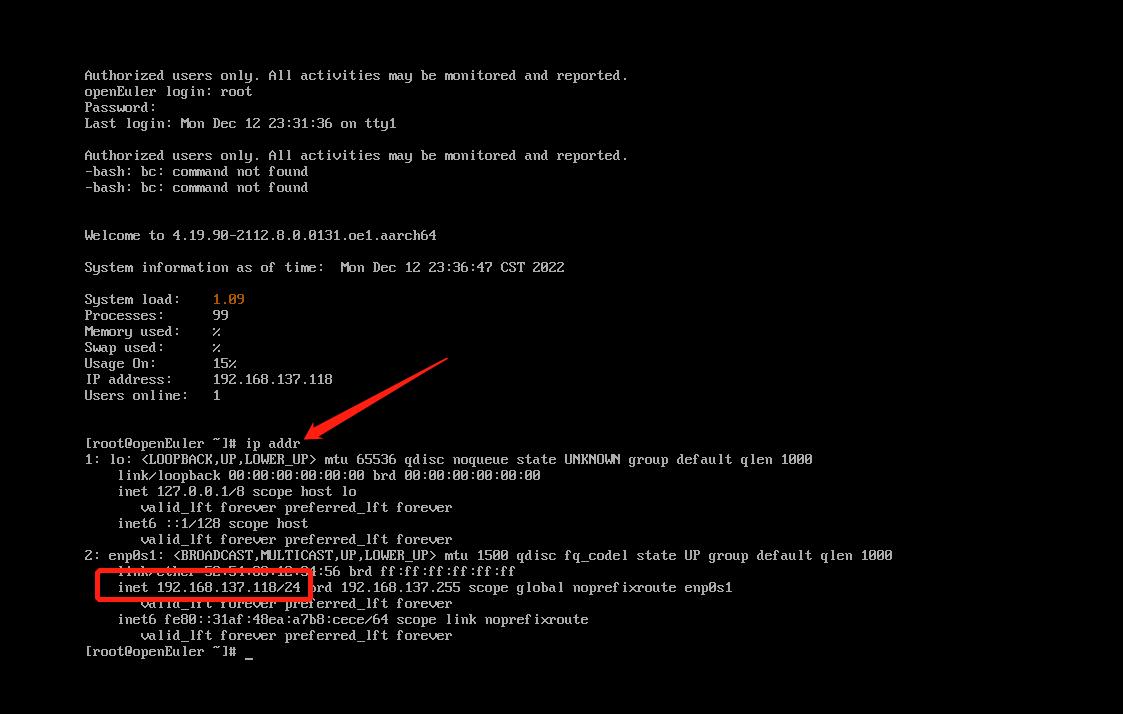
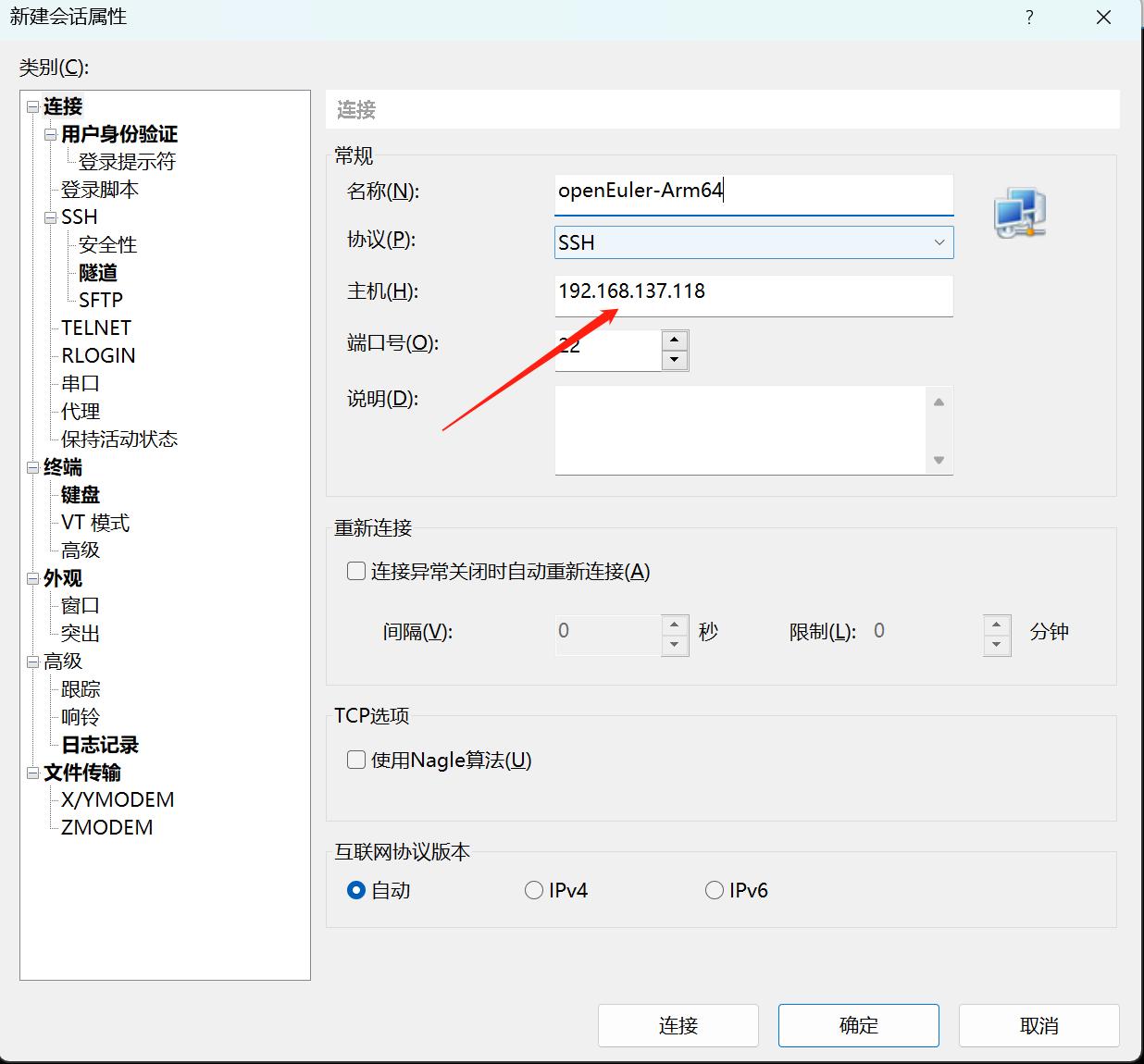
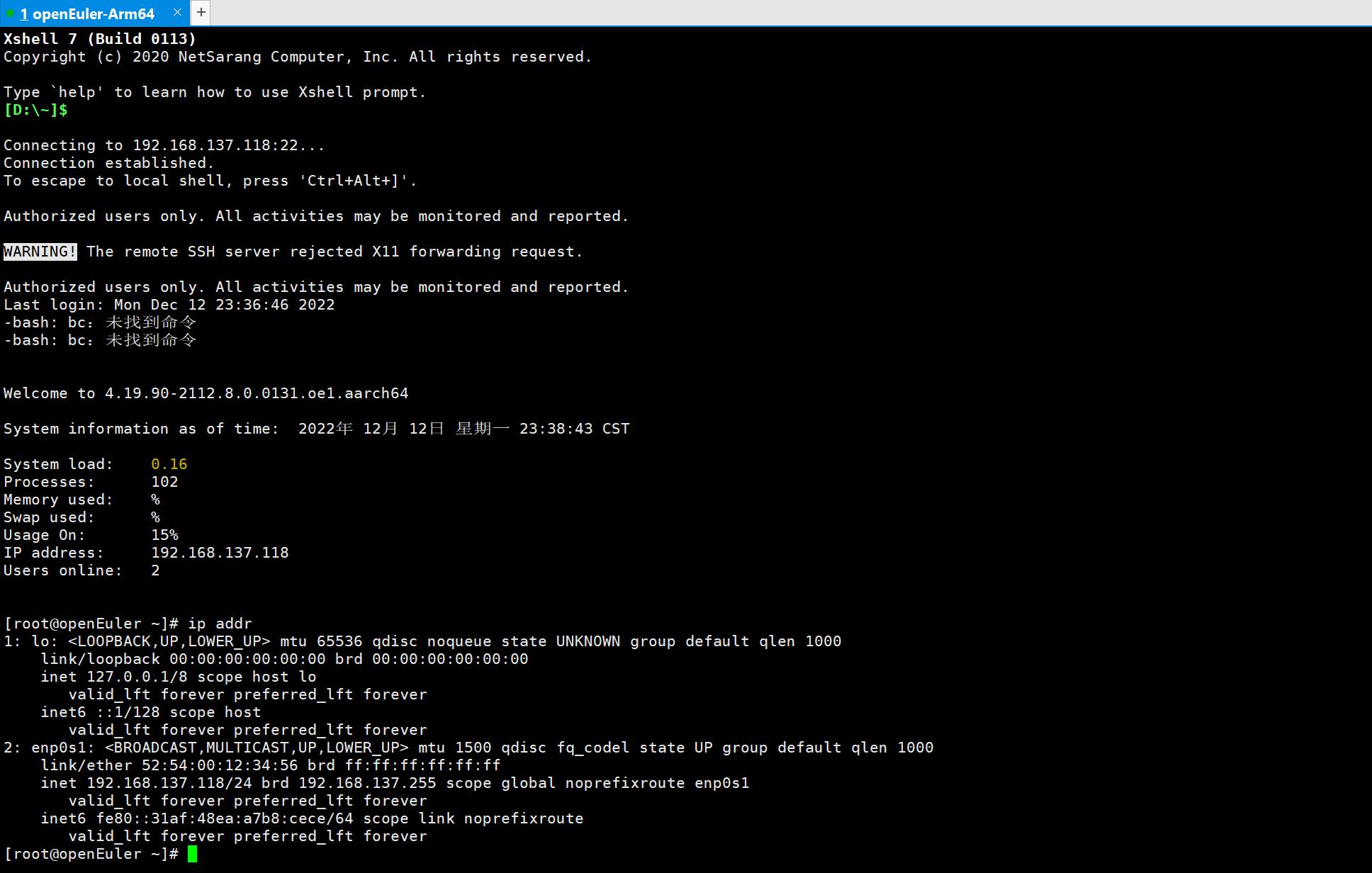
然后重启系统,查看 ip 地址后使用 Xshell 登录系统

一、引言
在当今数字化时代,图像处理已渗透到我们生活的方方面面,从日常使用的智能手机拍照美化,到医学领域的精准诊断,再到自动驾驶中的环境感知,其重要性不言而喻。在图像处理领域中,OpenCV 和频域分析,成为众多开发者和研究者不可或缺的强大工具。
OpenCV 作为一个开源且功能强大的计算机视觉库,提供了丰富的图像处理算法和工具,涵盖图像滤波、特征提取、目标检测等众多领域。其简单易用的接口,使得开发者能够快速搭建图像处理应用,大大降低了开发门槛。无论是刚入门的新手,还是经验丰富的专家,都能在 OpenCV 中找到解决问题的方法。
而频域分析则从另一个维度揭示了图像的奥秘。通过傅里叶变换等数学工具,将图像从空间域转换到频率域,我们可以深入了解图像的频率特性。低频部分代表着图像的平滑区域和大致轮廓,高频部分则对应着图像的细节、边缘和纹理。这种全新的视角为图像处理带来了更多的可能性,如频域滤波可以有效地去除噪声、增强图像的特定频率成分,从而实现图像的去噪、锐化等操作 。
接下来,让我们一同深入探索 OpenCV 和 频域分析技术。
二、OpenCV:图像处理的基石
2.1 OpenCV 简介
OpenCV(Open Source Computer Vision Library)是一个开源的计算机视觉库,最初由英特尔公司于 1999 年创建,后逐渐发展成为全球开发者广泛使用的重要工具 。它具有跨平台的特性,能够在 Windows、Linux、macOS、Android 和 iOS 等多种操作系统上稳定运行,为不同平台的开发者提供了一致的开发体验。同时,OpenCV 支持 C++、Python、Java 等多种编程语言,开发者可以根据自身的技术栈和项目需求选择熟悉的语言进行开发,极大地降低了学习成本和开发门槛。
OpenCV 拥有超过 2500 个优化算法和函数,涵盖了图像处理、特征检测与提取、物体识别与跟踪、摄像机标定、深度估计等众多计算机视觉领域。从简单的图像滤波、边缘检测,到复杂的目标检测、人脸识别,OpenCV 都提供了丰富且高效的解决方案。其广泛应用于安防监控、自动驾驶、医学影像分析、工业检测、娱乐等多个领域,在安防监控中,利用 OpenCV 可以实现实时的目标检测与跟踪,保障公共安全;在自动驾驶领域,它助力车辆实现环境感知,识别道路、行人与障碍物,为自动驾驶的安全性和可靠性提供支持。
2.2 核心功能
-
图像读取、显示与保存:
cv2.imread()函数可以从文件中读取图像,支持多种常见的图像格式,如 JPEG、PNG、BMP 等。cv2.imshow()函数用于在窗口中显示图像,方便开发者直观地查看处理结果。cv2.imwrite()函数则能够将处理后的图像保存到指定路径,保存格式也可根据文件扩展名自动识别 。
在图像预处理阶段,读取图像是第一步操作,通过读取图像,后续才能进行各种处理,而显示图像可以帮助开发者实时查看处理效果,保存图像则是将最终结果留存。 -
色彩空间转换:现实生活中,不同的场景和需求需要使用不同的色彩空间来表示图像。OpenCV 提供了
cv2.cvtColor()函数,能够实现多种色彩空间之间的转换,如将常见的 BGR(Blue, Green, Red)颜色空间转换为灰度图、HSV(Hue, Saturation, Value)颜色空间等。在图像识别中,将彩色图像转换为灰度图可以简化计算,提高处理效率;而在基于颜色的目标检测中,HSV 颜色空间更有利于对特定颜色的物体进行检测。 -
几何变换:
cv2.resize()函数可对图像进行缩放操作,调整图像的大小,以适应不同的应用场景,如在图像压缩或适配不同分辨率的显示设备时经常用到。cv2.rotate()函数用于图像的旋转,能够按照指定的角度或方向旋转图像,这在图像矫正、图像增强等方面有重要应用。cv2.warpAffine()函数实现了仿射变换,通过对图像进行平移、旋转、缩放等组合操作,可实现图像的几何变换,常用于图像配准、目标定位等任务。
-
滤波:在图像采集和传输过程中,图像常常会受到噪声的干扰,影响图像的质量和后续处理。OpenCV 提供了多种滤波函数,如:
- 均值滤波
cv2.blur(): 通过计算邻域像素的平均值来平滑图像,去除噪声; - 高斯滤波
cv2.GaussianBlur(): 根据高斯分布对邻域像素进行加权平均,在去除高斯噪声方面效果显著; - 中值滤波
cv2.medianBlur(): 用邻域像素的中值代替中心像素的值,对于椒盐噪声有很好的抑制作用。
这些滤波操作在图像去噪、平滑处理中发挥着关键作用,能够提高图像的清晰度和可用性。
- 均值滤波
-
边缘检测:边缘是图像中重要的特征之一,它反映了图像中物体的轮廓和结构信息。OpenCV 中的
cv2.Canny()函数是常用的边缘检测算法,它通过计算图像的梯度幅值和方向,结合双阈值检测和边缘跟踪,能够准确地检测出图像的边缘。在目标识别、图像分割等应用中,边缘检测是提取目标特征的重要步骤,为后续的分析和处理提供基础。
2.3 关键函数实战使用
- 图像读取、显示与保存:
import cv2
# 读取图像,'./resource/image.jpg'为图像路径,cv2.IMREAD_COLOR表示以彩色模式读取
image = cv2.imread('./resource/image.jpg', cv2.IMREAD_COLOR)
# 显示图像,窗口标题为'Original Image'
cv2.imshow('Original Image', image)
# 等待按键,0表示无限期等待,直到有按键按下
cv2.waitKey(0)
# 保存图像为'./resource/new_image.jpg'
cv2.imwrite('./resource/new_image.jpg', image)
# 关闭所有窗口
cv2.destroyAllWindows()
class="hljs-button signin active" data-title="登录复制" data-report-click="{"spm":"1001.2101.3001.4334"}">






评论记录:
回复评论: