推荐|【欧拉回路】【图论】【并集查找】765. 情侣牵手

作者推荐

本文涉及知识点

欧拉回路图论并集查找

LeetCoce 765 情侣牵手

n 对情侣坐在连续排列的 2n 个座位上，想要牵到对方的手。
人和座位由一个整数数组 row 表示，其中 row[i] 是坐在第 i 个座位上的人的 ID。情侣们按顺序编号，第一对是 (0, 1)，第二对是 (2, 3)，以此类推，最后一对是 (2n-2, 2n-1)。
返回最少交换座位的次数，以便每对情侣可以并肩坐在一起。每次交换可选择任意两人，让他们站起来交换座位。
示例 1:
输入: row = [0,2,1,3]
输出: 1
解释: 只需要交换row[1]和row[2]的位置即可。
示例 2:
输入: row = [3,2,0,1]
输出: 0
解释: 无需交换座位，所有的情侣都已经可以手牵手了。
提示:
2n == row.length
2 <= n <= 30
n 是偶数
0 <= row[i] < 2n
row 中所有元素均无重复

欧拉回路

座位A坐着a1和b1，假设他们属于第a对情侣和第b队情侣。
b2左在座位C，如果a2也做在C，则b1和a2互换。A={a1,a2} C = {b1,b2}。交换一次a $\leftrightarrow$ b
如果a2不在座位C，则C={b2,c1} 则交换b1 c1 。变成A={a1,c1} {b1,b2}。
如果a2,c2都在D，则c1 $\leftrightarrow$ a2，变成A={a1,a2} B={b1,b2} C={c1,c2} 交换两次a $\leftrightarrow$ b a $\leftrightarrow$ c。
$\vdots$
这是一个解，下来来证明是最优解。
{a1,b1} {b2,c1},{c2,a2}
解法一： b $\rightarrow$ a $\rightarrow$ c
解法二： b $\rightarrow$ c $\rightarrow$ a 交换的结果： {a1,c1}{b1,b2}{c2,a1} $\rightarrow$ {a1,a2}{b1,b2}{c1,c2}
解法三：a $\rightarrow$ b $\rightarrow$ c 交换的结果：{a1,a2} { b2,c1 } {c2,b1} $\rightarrow$ {b1,b2}{a1,a2}{c1,c2}
解法四：a $\rightarrow$ c $\rightarrow$ b 交换的结果：{c2 b1} {b2 c1} {a1 a2} $\rightarrow$ {a1,a2}{b1,b2}{c1,c2}
解法五：c $\rightarrow$ a $\rightarrow$ b
解法六：c $\rightarrow$ b $\rightarrow$ a
把某对情侣看成无向图的顶点，如果两对情侣有人挨在一起（有必要调整)，则有边连接两者。如果同一对情侣挨着一起，则连接自己。所有顶点度数为2。 $\iff$ 若干欧拉回路。
每个回路的边数（定点数）减一就是需要调整次数。自环也符合此算法。
用并集查找计算各连通区域（欧拉回路）的数量。返回：n - 区域数量。
a $\rightarrow$ b 表示第a队情侣已经搞定，现在需要处理第b对情侣。
本题的解决过程就是：欧拉回路减去最后一条边。显然欧拉回路的边数不受起点和边影响。
选定起点和起点方向后，结果是确定的：
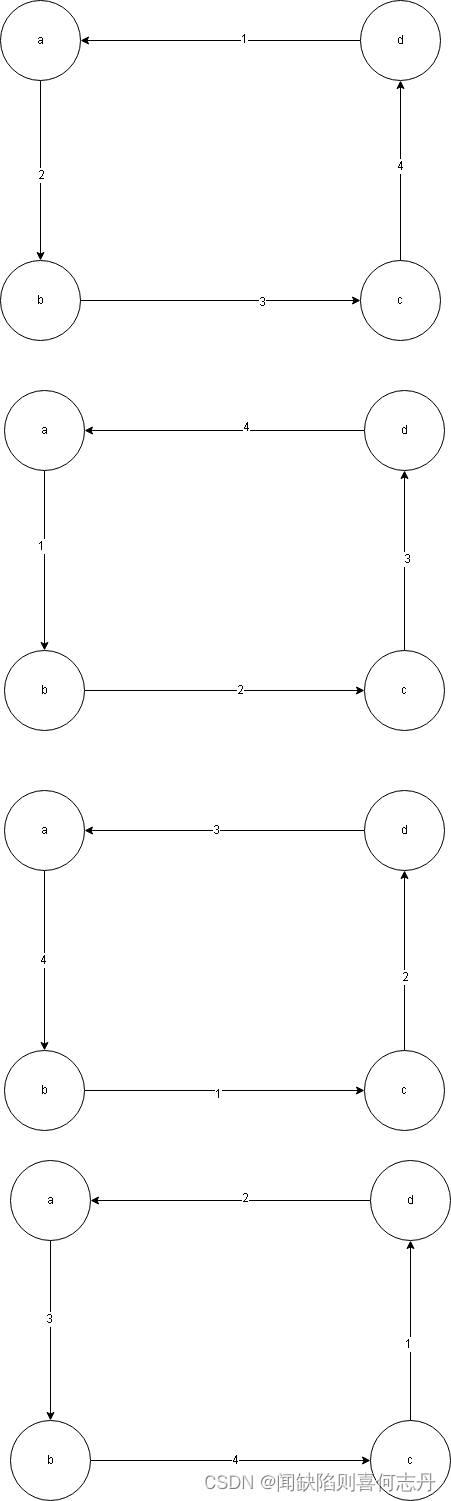
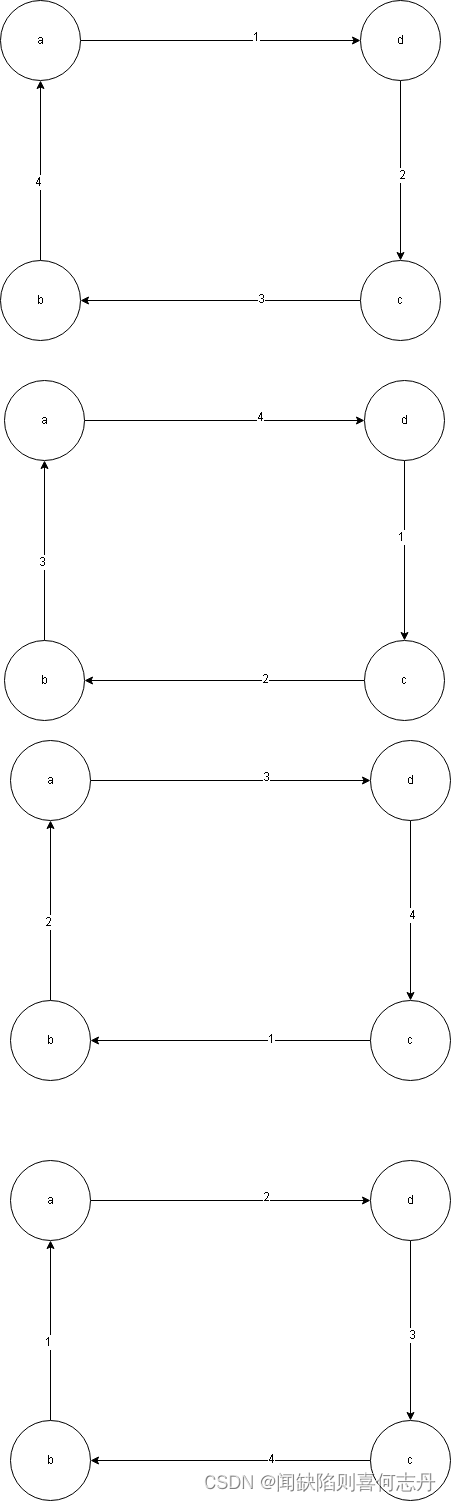
在这里插入图片描述

不失一般性，我们假定a $\rightarrow$ b 是第一条边。
初始：当前座位对{a,b}
a $\rightarrow$ b后：当前座位{b,d}
b $\rightarrow$ c后：当前座位{c,d}
c $\rightarrow$ d后:{d,d}
{d,d}无需处理。

代码

核心代码

class CUnionFind
{
public:
	CUnionFind(int iSize) :m_vNodeToRegion(iSize)
	{
		for (int i = 0; i < iSize; i++)
		{
			m_vNodeToRegion[i] = i;
		}
		m_iConnetRegionCount = iSize;
	}
	int GetConnectRegionIndex(int iNode)
	{
		int& iConnectNO = m_vNodeToRegion[iNode];
		if (iNode == iConnectNO)
		{
			return iNode;
		}
		return iConnectNO = GetConnectRegionIndex(iConnectNO);
	}
	void Union(int iNode1, int iNode2)
	{
		const int iConnectNO1 = GetConnectRegionIndex(iNode1);
		const int iConnectNO2 = GetConnectRegionIndex(iNode2);
		if (iConnectNO1 == iConnectNO2)
		{
			return;
		}
		m_iConnetRegionCount--;
		if (iConnectNO1 > iConnectNO2)
		{
			UnionConnect(iConnectNO1, iConnectNO2);
		}
		else
		{
			UnionConnect(iConnectNO2, iConnectNO1);
		}
	}

	bool IsConnect(int iNode1, int iNode2)
	{
		return GetConnectRegionIndex(iNode1) == GetConnectRegionIndex(iNode2);
	}
	int GetConnetRegionCount()const
	{
		return m_iConnetRegionCount;
	}
	vector<int> GetNodeCountOfRegion()//各联通区域的节点数量
	{
		const int iNodeSize = m_vNodeToRegion.size();
		vector<int> vRet(iNodeSize);
		for (int i = 0; i < iNodeSize; i++)
		{
			vRet[GetConnectRegionIndex(i)]++;
		}
		return vRet;
	}
	std::unordered_map<int, vector<int>> GetNodeOfRegion()
	{
		std::unordered_map<int, vector<int>> ret;
		const int iNodeSize = m_vNodeToRegion.size();
		for (int i = 0; i < iNodeSize; i++)
		{
			ret[GetConnectRegionIndex(i)].emplace_back(i);
		}
		return ret;
	}
private:
	void UnionConnect(int iFrom, int iTo)
	{
		m_vNodeToRegion[iFrom] = iTo;
	}
	vector<int> m_vNodeToRegion;//各点所在联通区域的索引,本联通区域任意一点的索引，为了增加可理解性，用最小索引
	int m_iConnetRegionCount;
};

class Solution {
public:
	int minSwapsCouples(vector<int>& row) {
		const int n = row.size() / 2;
		CUnionFind uf(n);
		for (int i = 0; i < n; i++)
		{
			uf.Union(row[i * 2] / 2, row[i * 2 + 1] / 2);
		}
		return n - uf.GetConnetRegionCount();
	}
};

测试用例

template<class T,class T2>
void Assert(const T& t1, const T2& t2)
{
	assert(t1 == t2);
}

template<class T>
void Assert(const vector<T>& v1, const vector<T>& v2)
{
	if (v1.size() != v2.size())
	{
		assert(false);
		return;
	}
	for (int i = 0; i < v1.size(); i++)
	{
		Assert(v1[i], v2[i]);
	}

}

int main()
{
	vector<int> row;
	{
		Solution sln;
		row = { 0, 2, 1, 3 };
		auto res = sln.minSwapsCouples(row);
		Assert(1, res);
	}
	{
		Solution sln;
		row = { 3,2,0,1 };
		auto res = sln.minSwapsCouples(row);
		Assert(0, res);
	}
}

2023年4月

//并集查找
class CUnionFind
{
public:
CUnionFind(int iSize)
{
for (int i = 0; i < iSize; i++)
{
m_vTop.emplace_back(i);
}
m_iSize = m_vTop.size();
}
void Add(int iFrom, int iTo)
{
const int iRoot1 = GetTop(iFrom);
const int iRoot2 = GetTop(iTo);
if (iRoot1 == iRoot2)
{
return;
}
m_vTop[iRoot1] = GetTop(iRoot2);
m_iSize–;
}
int GetTop(int iNode)
{
if (iNode == m_vTop[iNode])
{
return iNode;
}
return m_vTop[iNode] = GetTop(m_vTop[iNode]);
}
int Size()const
{
return m_iSize;
}
private:
vector m_vParent,m_vTop;
int m_iSize;
};

class Solution {
public:
int minSwapsCouples(vector& row) {
CUnionFind un(row.size()/2);
for (int i = 0; i < row.size(); i+=2)
{
un.Add(row[i] / 2, row[i + 1] / 2);
}
return row.size() / 2 - un.Size();
}
};

扩展阅读

视频课程

有效学习：明确的目标及时的反馈拉伸区（难度合适），可以先学简单的课程，请移步CSDN学院，听白银讲师（也就是鄙人）的讲解。
https://edu.csdn.net/course/detail/38771

如何你想快

速形成战斗了，为老板分忧，请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176

我想对大家说的话
闻缺陷则喜是一个美好的愿望，早发现问题，早修改问题，给老板节约钱。
子墨子言之：事无终始，无务多业。也就是我们常说的专业的人做专业的事。
如果程序是一条龙，那算法就是他的是睛

测试环境

操作系统：win7 开发环境： VS2019 C++17
或者操作系统：win10 开发环境： VS2022 C++17
如无特殊说明，本算法用**C++**实现。

文章知识点与官方知识档案匹配，可进一步学习相关知识

算法技能树首页概览60496 人正在系统学习中

群中有博文配套源码

QQ群名片

【欧拉回路】【图论】【并集查找】765. 情侣牵手