目录
一.光源种类
unity中的灯光主要有四种,合理使用可以实现任何灯光效果。
1.Directional Light(方向光,平行光)
Directional Light 是使用最多的一种光源,效果相当于现实世界中的太阳光。光源的位置和大小都不会影响物体的渲染效果,但是光方向会有影响。同时也是最省资源的一种光。
2.Point Light(点光源)
Point Light类似于灯泡,从一点向四面八方发射光线。影响该范围内的所有物体。但是比较耗资源。实际使用中大多采取烘焙的方式。
3.Spotlight(聚光灯)
Spotlight从一点向某个方向发出光线,按照圆锥体范围照射,类似于手电筒。
4.Area Light(区域光,面光源)
Area Light 使用较少,不能用于实时光照,通常用于光照烘焙。
二.光源属性
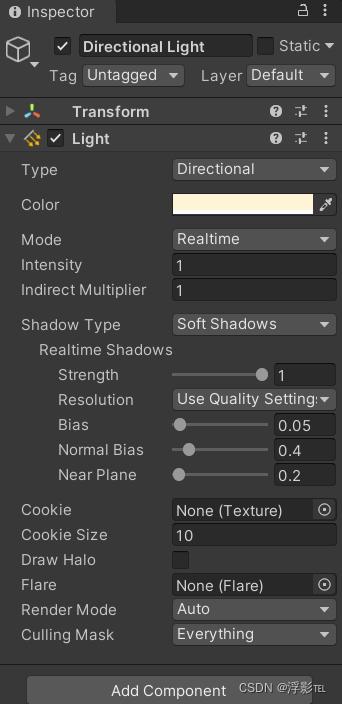
在light组件中有很多属性,下面介绍一些重要的属性。
1.Type 可以选择光的类型,也就是上面介绍的那四种。
2.Color 光的颜色。
3. Range 范围,控制点光源和聚光灯照射的范围距离,平行光没有这个属性。
4.Spot Angle 角度,控制聚光灯圆锥张角的大小,只有聚光灯有这个属性。
5.Intensity 强度 ,控制光照的强度。
6.Cookie 用于指定拥有alpha通道的纹理,意思是光线在不同的地方有着不同的亮度。如果光源是聚光灯或者方向光的话,就可以指定一个2D纹理,如果是点光源的话,必须指定一个cubemap纹理。Cookie的效果就类似于星光灯。通过调节不同位置灯光的亮度可以使光照射出指定的图案。
7.CookieSize 控制缩放Cookie投影。
8.Shadow Type 阴影类型, 一共有三种。
No Shadows(无阴影)
Hard Shadows(硬阴影)边缘锯齿比较明显,耗费资源较少。
Soft Shadows(软阴影)锯齿处理较好,阴影柔和真实,但是耗费资源较多。
Shadow下的参数介绍(No Shadows没有这些参数)
Strength 阴影强度,取值0-1,0代表没有阴影,1代表全黑。
Resolution 分辨率,控制阴影的质量
Bias 偏移量 阴影与物体之间的距离,取值0-0.5。
Normal Bias 微调阴影边缘。
Near Plane 近平面的值,当光源与物体的距离小于该值,则不会产生阴影。
9.Draw Halo 绘制光晕,开启光晕效果。
10.Flare 耀斑,指定耀斑镜头光晕的效果。
11.Render Mode 渲染模式
Auto 自动, 根据光源亮度和运行时质量设置来选择important还是not important
Important 重要, 光源进行逐像素渲染
Not Important 不重要, 光源以最快的速度渲染
12.Culling Mask,剔除遮蔽图,选中的层所关联的对象会受到光源照射的影响。在制作过程中需要剔除掉烘焙或者自发光的物体。
通常在一个场景中,往往不止有一个光,需要多种灯光相互配合才能达到我们想要的效果。比如在方向光方向相反再加上一个强度小一点的方向光来补光使物体背面不会显得特别暗。在黄昏的时候就需要光的颜色偏黄一点。
本文涉及的基础知识点
题目
得到 K 个半回文串的最少修改次数
给你一个字符串 s 和一个整数 k ,请你将 s 分成 k 个 子字符串 ,使得每个 子字符串 变成 半回文串 需要修改的字符数目最少。
请你返回一个整数,表示需要修改的 最少 字符数目。
注意:
如果一个字符串从左往右和从右往左读是一样的,那么它是一个 回文串 。
如果长度为 len 的字符串存在一个满足 1 <= d < len 的正整数 d ,len % d == 0 成立且所有对 d 做除法余数相同的下标对应的字符连起来得到的字符串都是 回文串 ,那么我们说这个字符串是 半回文串 。比方说 “aa” ,“aba” ,“adbgad” 和 “abab” 都是 半回文串 ,而 “a” ,“ab” 和 “abca” 不是。
子字符串 指的是一个字符串中一段连续的字符序列。
示例 1:
输入:s = “abcac”, k = 2
输出:1
解释:我们可以将 s 分成子字符串 “ab” 和 “cac” 。子字符串 “cac” 已经是半回文串。如果我们将 “ab” 变成 “aa” ,它也会变成一个 d = 1 的半回文串。
该方案是将 s 分成 2 个子字符串的前提下,得到 2 个半回文子字符串需要的最少修改次数。所以答案为 1 。
示例 2:
输入:s = “abcdef”, k = 2
输出:2
解释:我们可以将 s 分成子字符串 “abc” 和 “def” 。子字符串 “abc” 和 “def” 都需要修改一个字符得到半回文串,所以我们总共需要 2 次字符修改使所有子字符串变成半回文串。
该方案是将 s 分成 2 个子字符串的前提下,得到 2 个半回文子字符串需要的最少修改次数。所以答案为 2 。
示例 3:
输入:s = “aabbaa”, k = 3
输出:0
解释:我们可以将 s 分成子字符串 “aa” ,“bb” 和 “aa” 。
字符串 “aa” 和 “bb” 都已经是半回文串了。所以答案为 0 。
参数范围:
2 <= s.length <= 200
1 <= k <= s.length / 2
s 只包含小写英文字母。
分析
第一轮:vector
第二轮:int m_vNeedNum[200][201] 记录s[left,r)变成半回文需要改变的次数。
第三轮:三层循环,第一层循环:枚举k,第二层循环枚举s[0,j]。第三轮循环枚举m,[0,m]和(m,j]。
三轮时间复杂度都是:O(nnn);
核心代码
class Solution {
public:
int minimumChanges(string s, int k) {
m_c = s.length();
Init(s);
Init2(s);
vector pre(m_c);//pre[j]将s[0,j]拆分成i-1个子字符串,这些子串全部半回文的需要改变的字符数
for (int j = 0; j < m_c; j++)
{
pre[j] = m_vNeedNum[0][j + 1];
}
for (int i = 2; i <= k; i++)
{
vector dp(m_c);
for (int j = i - 1; j < m_c; j++)
{//拆分成[0,m]和(m,j]([m+1,j+1)),前者i-1个子串,后者一个子串
int iMin = INT_MAX;
for (int m = max(0,i-2); m < j; m++)
{
const int cur = pre[m] + m_vNeedNum[m + 1][j + 1];
iMin = min(iMin, cur);
}
dp[j] = iMin;
}
pre.swap(dp);
}
return pre.back();
}
void Init(std::string& s)
{
for(int i = 0 ; i < 2 ; i++ )
for (int j = 0; j <= m_c / 2; j++)
{
m_aDCenger[i][j].assign(m_c+1, vector((m_c+1)/2+1));
}
for (int d = 1; d <= m_c/2; d++)
{
for (int center = 0; center < m_c; center++)
{
int halfLen = 1;
while ((center + d* (halfLen-1) < m_c) && (center - d* (halfLen - 1) >= 0) )
{
m_aDCenger[1][d][center][halfLen] = m_aDCenger[1][d][center][halfLen - 1] +(s[center + d * (halfLen - 1)] != s[center - d * (halfLen - 1)]) ;
halfLen++;
}
}
for (int center = 0; center < m_c; center++)
{//偶数半回文
int halfLen = 1;
while ((center + d * halfLen < m_c) && (center - d * (halfLen - 1) >= 0) )
{
m_aDCenger[0][d][center][halfLen] = m_aDCenger[0][d][center][halfLen - 1] + (s[center + d * halfLen] != s[center - d * (halfLen - 1)]);
halfLen++;
}
}
}
}
void Init2(std::string& s)
{
memset(m_vNeedNum, sizeof(m_vNeedNum), 0);
for (int left = 0; left < m_c; left++)
{
for (int r = left + 1; r <= m_c; r++)
{
const int subLen = r - left;
int iNeed = 1000*1000;
for (int d = 1; (d * d <= subLen)&&(subLen >1); d++)
{
if (0 != subLen % d)
{
continue;
}
{
const int iCurNeed = DoLeftRightD(left, r, d);
iNeed = min(iNeed, iCurNeed);
}
if(d >1 )
{
const int iCurNeed = DoLeftRightD(left, r, subLen/d);
iNeed = min(iNeed, iCurNeed);
}
}
m_vNeedNum[left][r] = iNeed;
}
}
}
int DoLeftRightD(int left,int r,int d)
{
const int subLen = r - left;
const int len = subLen / d;
const auto& arr = m_aDCenger[len % 2];
const int midIndex = (len-1)/2;
int iCurNeed = 0;
for (int begin = 0; begin < d; begin++)
{
const int center = left + begin + midIndex * d;
iCurNeed += arr[d][center][(len + 1) / 2];
}
return iCurNeed;
}
int m_c;
vector
int m_vNeedNum[200][201];
};
测试用例
template
void Assert(const vector& v1, const vector& v2)
{
if (v1.size() != v2.size())
{
assert(false);
return;
}
for (int i = 0; i < v1.size(); i++)
{
assert(v1[i] == v2[i]);
}
}
template
void Assert(const T& t1, const T& t2)
{
assert(t1 == t2);
}
int main()
{
//string s = “bbacccbbaabbddddddddddddddddddddddddddddddddddddddddddddbbacccbbaabbdddddddddddddddddddddddddddddddddddddddddddddbbbacccbbaabbddddddddddddddddddddbbacccbbaabbdddddddddddddddddddddddddddddddddddddddddd”;
string s = “abcac”;
int k = 2;
Solution slu;
auto res = slu.minimumChanges(s,k);
Assert(1, res);
//CConsole::Out(res);
class="hljs-button signin active" data-title="登录复制" data-report-click="{"spm":"1001.2101.3001.4334"}">

 class="blog_extension_card_cont">
class="blog_extension_card_cont">


评论记录:
回复评论: