如何识别图像中“有什么”以及“是什么”？
计算机对图像的保存都是以像素值的方式，而且一个像素由红绿蓝三个值构成，也就是说比如某张图的大小是–100*100，那么它将会有100x100x3万个值，那么在这样的一堆数据中，谁才是我们需要的？什么决定了这幅图“是什么”“有什么”“表达什么”呢？

受哺乳动物视觉系统的结构启发，人们引入了一个处理图片的强大模型结构，后来发展成了现代卷积网络的基础。所谓卷积引自数学中的卷积运算：
$$S(t)=\int x(t-a)w(a)da$$
它的意义在于，处理信号或图像领域内的互相关（cross-correlation），比如有一段时间内的股票或者其他的测量数据，显然时间离当下越近的数据与结果越相关，作用越大，所以在处理数据时可以采用一种局部加权平均的方法，这就叫卷积，其离散形式为：
$$S(t)=\sum _{a}x(t-a)w(a)$$
公式中的第一个参数x是输入的数据，第二参数w叫核函数，a表示时间t的时间间隔（滑动），而函数的输出可以被叫做特征映射（feature map）。也就是说完成特征映射的过程叫卷积，不过是某一个东西和另一个东西在时间维度上的“叠加”作用。而使用卷积运算的重要作用就是，通过卷积运算，可以使原信号特征增强，并且降低噪音。

• 关于“卷”和“积”，卷是指函数的翻转，即x(a)变成了x(-a)，然后为了对齐时间线将平移n；“积”是与w的乘。之所以要这样就是为了局部的加权平均，信号增强。

卷积神经网络里的卷积层为：
按卷积原本的定义，互相关是两个函数之间的滑动点积或内积，先卷（翻转，平移），再积（相乘）。所以直观来说，就是将卷积核（已有翻转的处理）在输入的矩阵中进行“滑动”，并且两两相乘得到一个代替的值。如下图3x4的输入在2x2的卷积后，变成了2x3的结果。

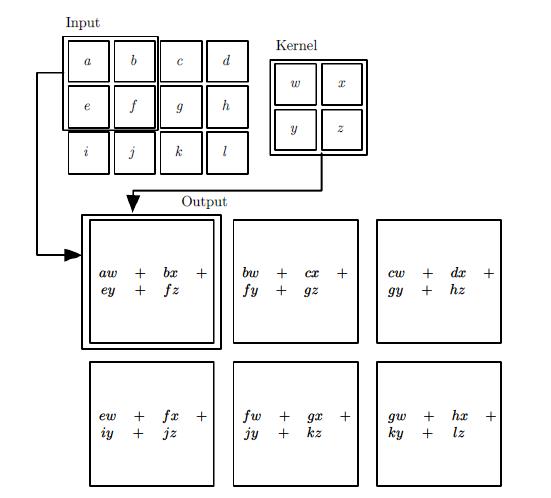
卷积过程采用了稀疏交互（Sparse interactions），参数共享（parameter sharing），等变表示（equivariant representations） 三大思想。稀疏交互是利用了局部感受野（local receptive fields，即输入仅仅至于感受野比如3x3=9，这9个数有关），限制了空间的大小，参数共享就是权值共享（即如果过滤器适合了输入图像矩阵某一部分，理论上它也同样适合其他特征的检测，于是整个都使用一个卷积核）不但能减少参数数量（特别是相比普通的神经网络，节省了大量的参数），还能控制模型规模，增强模型的泛化能力。

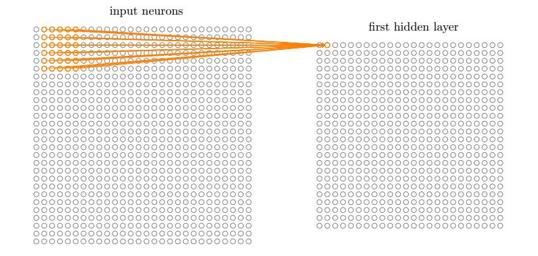
而卷积为什么有效？

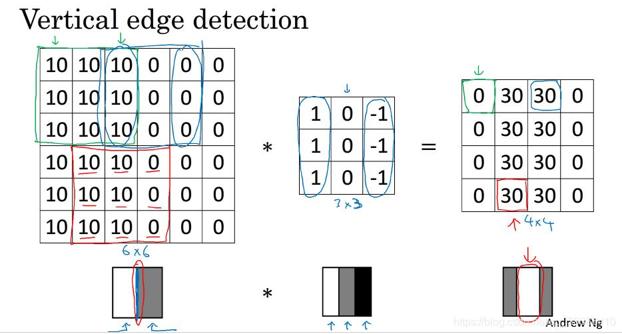
显然如果10代表明亮的图，0是灰色，那么经过卷积核的处理后，将会出现最右的明亮分割线。而这样的卷积核实际上可以理解为左边的1和右边-1有着明显的差距，而我们需要找出这个差距，所以利用这样的卷积核可以很容易的发现一些特征。

卷积的傅里叶变换视角
傅里叶变换可以看作是把数据从空间域转变为频率域的形式，而且可以有十分清晰的划分（特别是对高频和低频）。卷积定理中提到，两个矩阵的卷积结果等于两个矩阵经过傅里叶变换后，进行元素级别的乘法，再进行反向的傅里叶变换处理。

经过卷积层的学习输出会是：
$$Sigmoid(\sum S(t)+b)$$

卷积神经网络里的池化层为：
池化层也称亚采样层（Subsampling Layer），简单来说，就是利用其局部相关性，在“采样”数据的同时还保留了有用信息。巧妙的采样还具备局部线性转换不变性（translation invariant），即如果选用连续范围作为池化区域，并且只是池化相同的隐藏单元产生的特征，那么池化单元就具有平移不变性，这意味着即使图像有一个小平移，依然会产生相同的池化特征，这种网络结构对于平移，比例缩放，倾斜，或者共他形式的变形具有高度不变性。而且使用池化可以看作是增加了一个无限强的先验，卷积层学得的函数必须具有对少量平移的不变性，从而增强卷积神经网络的泛化处理能力，预防网络过拟合。而且这样聚合的最直接目的是可以大大降低下一层待处理的数据量，降低了网络的复杂度，减少了参数数量。
池化函数使用某一位置的相邻输出的总计特征来代替网络在该位置的输出，常见的统计特性有最大值、均值、累加和及L2范数等。

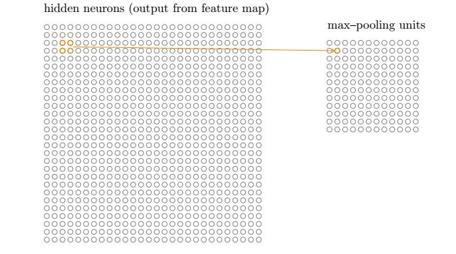
如图所示，池化层的输出是：$$Sigmoid(aW+b)$$
不过在实践中，有时可能会希望跳过核的一些位置来降低计算开销，由此产生了步幅（stride）。
零填充（zero-padding）以获取低维度：此操作通常用于边界处理。因为有时候卷积核的大小并不一定刚好就被输入数据矩阵的维度大小乘除。因此就可能会出现卷积核不能完全覆盖边界元素的情况，逼迫我们“二选一”，另外按照卷积的方法，越中间的将会被使用的最后，相比之下边缘部分使用的太少了，会损失相应的一些边缘信息。所以这时候就需要在输入矩阵的边缘使用零值进行填充来解决这个问题。而且通过pad操作可以更好的控制特征图的大小。使用零填充的卷积叫做泛卷积（wide convolution），不适用零填充的叫做严格卷积（narrow convolution）。

卷积神经网络里的全连接层为：

全连接层（Fully Connected Layer，简称FC）。“全连接”意味着，前层网络中的所有神经元都与下一层的所有神经元连接。全连接层设计目的在于，它将前面各个层学习到的“分布式特征表示”，映射到样本标记空间，然后利用损失函数来调控学习过程，最后给出对象的分类预测。不同于BP全连接网络的是，卷积神经网络在输出层使用的激活函数不同，比如说它可能会使用Softmax函数，ReLU函数等）。

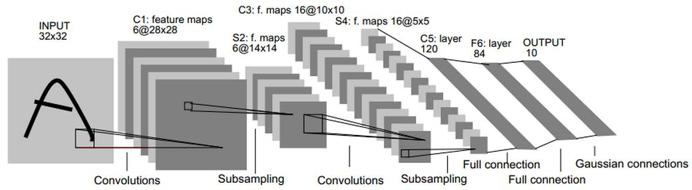
比如上图网络的具体步骤是：

输入为32×32的原图像。
第一层是卷积层C1，经过5×5的的感受野，有6个卷积核，形成6个28×28的特征映射。这层的参数个数为5*5*6+6（偏置项的个数）
第二层是池化层S2，用于实现抽样和池化平均，经过2×2的的感受野，形成6个14×14的特征映射。这层的参数个数为[1（训练得到的参数）+1（训练得到的偏置项）]×6=12
第三层是卷积层C3，与第一层一样，形成16个10×10的特征映射。参数个数为5*5*16+16=416
第四层是池化层S4，与第二层一样，形成16个5×5的特征映射。参数个数为（1+1）*16=32
之后就是120个神经元，64个神经元全连接而成的全连接层，最后得到径向基函数输出结果。
1
2
3
4
5
6

正向传播完成后，将结果与真实值做比较，然后极小化误差反向调整权值矩阵。

TF应用：
CIFAR-10 数据集的分类。
参数说明：
conv2d(input, filter, strides, padding, use_cudnn_on_gpu=None,data_format=None, name=None)

input：输入的数据。格式为张量。[batch, in_height, in_width, in_channels]。
批次，高度，宽度，输入通道数。 
filter：卷积核。格式为[filter_height, filter_width, in_channels, out_channels]。
高度，宽度，输入通道数，输出通道数。 
strides：步幅 [1，水平步长，垂直步长，1]，前后必须为1
padding：如果是SAME，则保留图像周圈不完全卷积的部分，即会补0。VALID相反。
use_cudnn_on_gpu：是否使用cudnn加速
1
2
3
4
5
6
7

max_pool(value, ksize, strides, padding, data_format=“NHWC”, name=None)

value：张量，格式为[batch, height, width, channels]。
批次，高度，宽度，输入通道数。
ksize：窗口大小
strides：步幅 [1，水平步长，垂直步长，1]，前后必须为1
padding：如果是SAME，则保留图像周圈不完全卷积的部分。VALID相反。
1
2
3
4
5

import tensorflow as tf 
import tensorflow.examples.tutorials.mnist.input_data as input_data

mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)#下载mnist数据集
x = tf.placeholder(tf.float32, [None, 784])#28X28的图像大小
#one-hot编码，10位数。[0,0,1,0,0,0,0,0,0,0,0,]表示数字2.
y_actual = tf.placeholder(tf.float32, shape=[None, 10])

#初始化权值 W
def weight_variable(shape):
  initial = tf.truncated_normal(shape, stddev=0.1)#正太分布，标准差0.1
  return tf.Variable(initial)

#初始化偏置项 b
def bias_variable(shape):
  initial = tf.constant(0.1, shape=shape)
  return tf.Variable(initial)
  
#卷积层，参数见前文
def conv2d(x, W):
  return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding='SAME')

#池化层，参数见前文
def max_pool(x):
  return tf.nn.max_pool(x, ksize=[1, 2, 2, 1],strides=[1, 2, 2, 1], padding='SAME')

#搭建CNN
x_image = tf.reshape(x, [-1,28,28,1])#转换输入数据shape，-1指自动确定，最后的1表示颜色通道数
W_conv1 = weight_variable([5, 5, 1, 32])#卷积核大小
b_conv1 = bias_variable([32]) #偏置项
h_conv1 = tf.nn.relu(conv2d(x_image, W_conv1) + b_conv1)#第一个卷积层，relu激活函数
h_pool1 = max_pool(h_conv1)#第一个池化层，最大池化

W_conv2 = weight_variable([5, 5, 32, 64])
b_conv2 = bias_variable([64])
h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2) + b_conv2)#第二个卷积层
h_pool2 = max_pool(h_conv2)#第二个池化层

W_fc1 = weight_variable([7 * 7 * 64, 1024])
b_fc1 = bias_variable([1024])
h_pool2_flat = tf.reshape(h_pool2, [-1, 7*7*64])
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)#第一个全连接层，matmul是矩阵乘法。而tf.multiply是点乘

keep_prob = tf.placeholder("float") #dropout保留概率
h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob)#dropout层，减少过拟合

#将1024为变成10维，即输出0~9的分类
W_fc2 = weight_variable([1024, 10])
b_fc2 = bias_variable([10])
y_predict=tf.nn.softmax(tf.matmul(h_fc1_drop, W_fc2) + b_fc2)#softmax激活函数

cross_entropy = -tf.reduce_sum(y_actual*tf.log(y_predict))#交叉熵损失函数，reduce_sum用于求和
train_step = tf.train.GradientDescentOptimizer(1e-3).minimize(cross_entropy)#梯度下降
correct_prediction = tf.equal(tf.argmax(y_predict,1), tf.argmax(y_actual,1)) #argmax取最大值的下标，返回true or false
accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))#计算准确度，mean计算平均值，cast用于转换类型，true会变为1

sess=tf.InteractiveSession()#初始化          
sess.run(tf.global_variables_initializer())
for i in range(20000):#内存小的请谨慎设定迭代次数
  batch = mnist.train.next_batch(50)
  if i%100 == 0:#每100次查看进程
    train_acc = accuracy.eval(feed_dict={x:batch[0], y_actual: batch[1], keep_prob: 1.0})#eval是tf.Tensor的Session.run()，启动计算
    print ('step %d, training accuracy %g'%(i,train_acc))
    train_step.run(feed_dict={x: batch[0], y_actual: batch[1], keep_prob: 0.5})

test_acc=accuracy.eval(feed_dict={x: mnist.test.images, y_actual: mnist.test.labels, keep_prob: 1.0})
print ("test accuracy %g"%test_acc)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68

如果用keras实现则是：

from keras import layers
from keras.models import Model

def lenet_5(in_shape=(32,32,1), n_classes=10, opt='sgd'):
   in_layer = layers.Input(in_shape)
   conv1 = layers.Conv2D(filters=20, kernel_size=5,
                         padding='same', activation='relu')(in_layer)
   pool1 = layers.MaxPool2D()(conv1)
   conv2 = layers.Conv2D(filters=50, kernel_size=5,
                         padding='same', activation='relu')(pool1)
   pool2 = layers.MaxPool2D()(conv2)
   flatten = layers.Flatten()(pool2)#flatten后好输入到全连接层
   dense1 = layers.Dense(500, activation='relu')(flatten)
   preds = layers.Dense(n_classes, activation='softmax')(dense1)

   model = Model(in_layer, preds)
   model.compile(loss="categorical_crossentropy", optimizer=opt,
               metrics=["accuracy"]) #直接定义损失函数，优化器，计算值
   return model

if __name__ == '__main__':
   model = lenet_5()
   print(model.summary())
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

卷积到底抽象了些什么？

从上图的过程可视化，可以看到每一层都完成了一定程度特征组合和抽象，最后映射到确定的某类。同最后的输入one-hot可以看到，数字3的地方最亮，便就是最后的结果。

CNN在图像中应用广泛的原因是什么？

• 局部连。捕获局部相关性，类似滤波器，得到不同形态的feature map。
• 权值共享、减少参数量
• 池化，增大感受野。减少参数个数，控制过拟合，增加鲁棒性，到达尺度不变性（即不论物体在图像中的哪个方位都可以被检测到。）
• 多层次，同时提取low-level 和 high-level信息

平均池化与最大池化

• 最大池化会倾向捕捉边缘这种尖锐突出的关键特征，平均倾向保留背景信息，而且其实能有减少结果方差的效果
• 两者在反向梯度的时候计算也不一样，所以速度上存在差异
• 为什么没有最小池化？图片最小像素可能为0，最小将完全提取不到特征
• 两者的反向传播差别：mean的前向是取了平均，那么反向也是把梯度给平均分配，这样来保证池化前后的梯度残差不变；max在前向是传了最大值，那么反向也只是把梯度传给最大的像素，其他像素不接受梯度，即为0.

为什么卷积核一般是奇数

• 方便存在中心做滑动时的定位参考点
• 方便在padding的时候，能够分配给两边。（如保持维度不变，只有池化才减少维度的卷积时，$\frac{n-f+2p}{s}+1=n$，s为1，$p=\frac{f-1}{2}$，所以如果卷积核是偶数了，那么padding会变成奇数，不足够分给两边形成对称）

什么时候不适合用CNN？

• 数据集太小，样本不足（深度学习在这里没有任何优势，提取特征非常容易过拟合，没有泛化能力）
• 数据集没有局部相关性（图像，语音，文字都是具有局部相关性的）

CNN发展变体集合：

卷积只能在同一组进行吗？– Group convolution

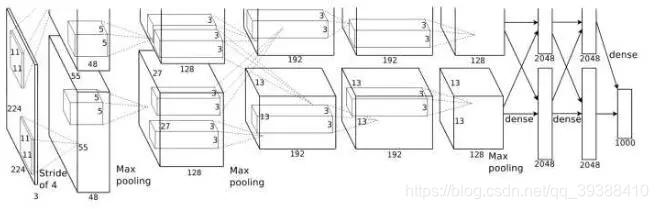
分组卷积最早在AlexNet中出现，由于当时的硬件资源有限，训练AlexNet时卷积操作不能全部放在同一个GPU处理，因此作者把feature maps分给多个GPU分别进行处理，具体架构包括5个卷积层和3个全连接层。这八层也都采用了当时的两个新概念——最大池化和Relu激活（以往更喜欢平均池化和Sigmoid等，如lenet）来为模型提供优势，最后把多个GPU的结果进行融合。
Alexnet：引入了dropout，ReLU，数据增强+池化可覆盖，3卷积1池化+3全连接层的套路。

from keras import layers
from keras.models import Model

def alexnet(in_shape=(227,227,3), n_classes=1000, opt='sgd'):
   in_layer = layers.Input(in_shape)
   conv1 = layers.Conv2D(96, 11, strides=4, activation='relu')(in_layer)
   pool1 = layers.MaxPool2D(3, 2)(conv1)
   conv2 = layers.Conv2D(256, 5, strides=1, padding='same', activation='relu')(pool1)
   pool2 = layers.MaxPool2D(3, 2)(conv2)
   conv3 = layers.Conv2D(384, 3, strides=1, padding='same', activation='relu')(pool2)
   conv4 = layers.Conv2D(256, 3, strides=1, padding='same', activation='relu')(conv3)
   pool3 = layers.MaxPool2D(3, 2)(conv4)
   flattened = layers.Flatten()(pool3)
   dense1 = layers.Dense(4096, activation='relu')(flattened)
   drop1 = layers.Dropout(0.5)(dense1)
   dense2 = layers.Dense(4096, activation='relu')(drop1)
   drop2 = layers.Dropout(0.5)(dense2)
   preds = layers.Dense(n_classes, activation='softmax')(drop2)

   model = Model(in_layer, preds)
   model.compile(loss="categorical_crossentropy", optimizer=opt,
               metrics=["accuracy"])
   return model

if __name__ == '__main__':
   model = alexnet()
   print(model.summary())
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

卷积核一定越大越好？– 3×3卷积核
AlexNet中用到了一些非常大的卷积核，比如11×11、5×5卷积核，之前人们的观念是，卷积核越大，receptive field（感受野）越大，看到的图片信息越多，因此获得的特征越好。但是大的卷积核会导致计算量的暴增，不利于模型深度的增加，计算性能也会降低。于是在VGG（最早使用，代码如下）、Inception网络中，利用2个3×3卷积核的组合比1个5×5卷积核的效果更佳，同时参数量（3×3×2+1 VS 5×5×1+1）被降低，因此后来3×3卷积核被广泛应用在各种模型中。
VGG：1 * 1卷积 和 3 * 3卷积，2 * 2池化使网络变深。常用VGG16和VGG19.

from keras import layers
from keras.models import Model, Sequential

from functools import partial

conv3 = partial(layers.Conv2D,
               kernel_size=3,
               strides=1,
               padding='same',
               activation='relu')

def block(in_tensor, filters, n_convs):
   conv_block = in_tensor
   for _ in range(n_convs):
       conv_block = conv3(filters=filters)(conv_block)
   return conv_block

def _vgg(in_shape=(227,227,3),
        n_classes=1000,
        opt='sgd',
        n_stages_per_blocks=[2, 2, 3, 3, 3]):
   in_layer = layers.Input(in_shape)

   block1 = block(in_layer, 64, n_stages_per_blocks[0])
   pool1 = layers.MaxPool2D()(block1)
   block2 = block(pool1, 128, n_stages_per_blocks[1])
   pool2 = layers.MaxPool2D()(block2)
   block3 = block(pool2, 256, n_stages_per_blocks[2])
   pool3 = layers.MaxPool2D()(block3)
   block4 = block(pool3, 512, n_stages_per_blocks[3])
   pool4 = layers.MaxPool2D()(block4)
   block5 = block(pool4, 512, n_stages_per_blocks[4])
   pool5 = layers.MaxPool2D()(block5)
   flattened = layers.GlobalAvgPool2D()(pool5)

   dense1 = layers.Dense(4096, activation='relu')(flattened)
   dense2 = layers.Dense(4096, activation='relu')(dense1)
   preds = layers.Dense(1000, activation='softmax')(dense2)

   model = Model(in_layer, preds)
   model.compile(loss="categorical_crossentropy", optimizer=opt,
               metrics=["accuracy"])
   return model

def vgg16(in_shape=(227,227,3), n_classes=1000, opt='sgd'):
   return _vgg(in_shape, n_classes, opt)

def vgg19(in_shape=(227,227,3), n_classes=1000, opt='sgd'):
   return _vgg(in_shape, n_classes, opt, [2, 2, 4, 4, 4])

if __name__ == '__main__':
   model = vgg19()
   print(model.summary())
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53

每层卷积只能用一种尺寸的卷积核？– Inception结构
传统的层叠式网络，基本上都是一个个卷积层的堆叠，每层只用一个尺寸的卷积核，例如VGG结构中使用了大量的3×3卷积层。事实上，同一层feature map可以分别使用多个不同尺寸的卷积核，以获得不同尺度的特征，再把这些特征结合起来 （如1x1，3x3，5x5等，然后让网络自己学习如何形成一个最合适的过滤器！这在一开始不知道如何选择卷积核时是很好的选择。），得到的特征往往比使用单一卷积核的要好，谷歌的GoogleNet。但是同样的，参数量加大，计算量会暴增。

怎样才能减少卷积层参数量？– Bottleneck
Inception结构中加入了一些1×1的卷积核降维！如下图，按照inception的特点，融合了1x1，3x3，5x5，为了减少参数分别在他们前面加入了一个1x1（当然它自己就不需要了）。至于最右部分是它的最大池化，因为最大池化后的通道会变很多，我们不喜欢最后的拼接它占大部分，所以再加入1x1进行降维。

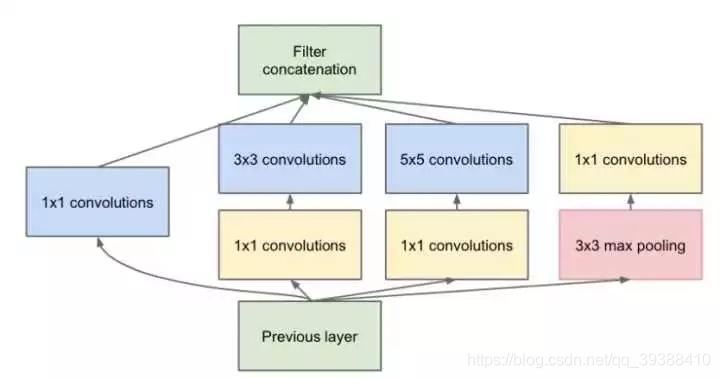
至于为什么能减少参数：如果一个n维的直接进过3x3卷积，将会有nx3x3xn的参数(若输出也为n维)，如果在前后各加一层1x1,则会有n×1×1×(n/4) + (n/4)×3×3×(n/4) + (n/4)×1×1×n，将会大大减少参数。所以1×1卷积核也被认为是影响深远的操作，往后大型的网络为了降低参数量都会应用上1×1卷积核。

1x1的作用

• 实现升维或者降维，减少参数
• 对不同特征进行归一化
• 在不同的channel上进行特征融合

GoogLeNet/Inception ：去掉全连接，全局平均池化来代替；inception结构；提出Batch Normalization。
架构实现如下：

from keras import layers
from keras.models import Model

from functools import partial

conv1x1 = partial(layers.Conv2D, kernel_size=1, activation='relu')
conv3x3 = partial(layers.Conv2D, kernel_size=3, padding='same', activation='relu')
conv5x5 = partial(layers.Conv2D, kernel_size=5, padding='same', activation='relu')

def inception_module(in_tensor, c1, c3_1, c3, c5_1, c5, pp):
   conv1 = conv1x1(c1)(in_tensor)

   conv3_1 = conv1x1(c3_1)(in_tensor)
   conv3 = conv3x3(c3)(conv3_1)

   conv5_1 = conv1x1(c5_1)(in_tensor)
   conv5 = conv5x5(c5)(conv5_1)

   pool_conv = conv1x1(pp)(in_tensor)
   pool = layers.MaxPool2D(3, strides=1, padding='same')(pool_conv)

   merged = layers.Concatenate(axis=-1)([conv1, conv3, conv5, pool])
   return merged

def aux_clf(in_tensor):
   avg_pool = layers.AvgPool2D(5, 3)(in_tensor)
   conv = conv1x1(128)(avg_pool)
   flattened = layers.Flatten()(conv)
   dense = layers.Dense(1024, activation='relu')(flattened)
   dropout = layers.Dropout(0.7)(dense)
   out = layers.Dense(1000, activation='softmax')(dropout)
   return out

def inception_net(in_shape=(224,224,3), n_classes=1000, opt='sgd'):
   in_layer = layers.Input(in_shape)

   conv1 = layers.Conv2D(64, 7, strides=2, activation='relu', padding='same')(in_layer)
   pad1 = layers.ZeroPadding2D()(conv1)
   pool1 = layers.MaxPool2D(3, 2)(pad1)
   conv2_1 = conv1x1(64)(pool1)
   conv2_2 = conv3x3(192)(conv2_1)
   pad2 = layers.ZeroPadding2D()(conv2_2)
   pool2 = layers.MaxPool2D(3, 2)(pad2)

   inception3a = inception_module(pool2, 64, 96, 128, 16, 32, 32)
   inception3b = inception_module(inception3a, 128, 128, 192, 32, 96, 64)
   pad3 = layers.ZeroPadding2D()(inception3b)
   pool3 = layers.MaxPool2D(3, 2)(pad3)

   inception4a = inception_module(pool3, 192, 96, 208, 16, 48, 64)
   inception4b = inception_module(inception4a, 160, 112, 224, 24, 64, 64)
   inception4c = inception_module(inception4b, 128, 128, 256, 24, 64, 64)
   inception4d = inception_module(inception4c, 112, 144, 288, 32, 48, 64)
   inception4e = inception_module(inception4d, 256, 160, 320, 32, 128, 128)
   pad4 = layers.ZeroPadding2D()(inception4e)
   pool4 = layers.MaxPool2D(3, 2)(pad4)

   aux_clf1 = aux_clf(inception4a)
   aux_clf2 = aux_clf(inception4d)

   inception5a = inception_module(pool4, 256, 160, 320, 32, 128, 128)
   inception5b = inception_module(inception5a, 384, 192, 384, 48, 128, 128)
   pad5 = layers.ZeroPadding2D()(inception5b)
   pool5 = layers.MaxPool2D(3, 2)(pad5)

   avg_pool = layers.GlobalAvgPool2D()(pool5)
   dropout = layers.Dropout(0.4)(avg_pool)
   preds = layers.Dense(1000, activation='softmax')(dropout)

   model = Model(in_layer, [preds, aux_clf1, aux_clf2])
   model.compile(loss="categorical_crossentropy", optimizer=opt,
               metrics=["accuracy"])
   return model

if __name__ == '__main__':
   model = inception_net()
   print(model.summary())
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77

越深的网络就越难训练吗？– Resnet残差网络
paper: https://arxiv.org/abs/1512.03385

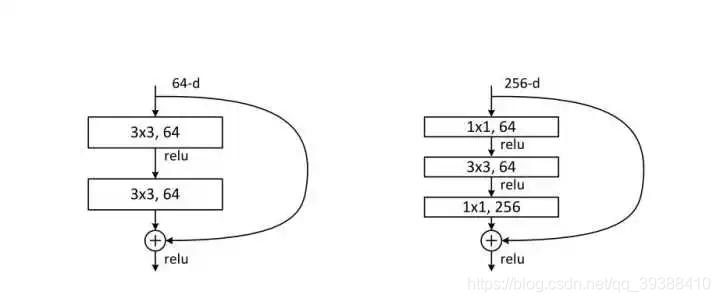
传统的卷积层层叠网络会遇到一个问题，当层数加深时，网络的表现越来越差，很大程度上的原因是因为当层数加深时，梯度消失得越来越严重，以至于反向传播很难训练到浅层的网络。直接映射是很难学习的，所以不去学习网络输出层与输入层间的映射，而是学习它们之间的差异——残差，即使信息可以跳过主路，直接传递。

• 实际使用时往往会在激活函数前使用BN，使用BN后可以不用去理会过拟合中drop out、L2正则项参数的选择问题，甚至可以移除这两项参数，或者可以选择更小的L2正则约束参数了，因为BN具有提高网络泛化能力的特性。
• 但是之所以BN放在激活函数之前，作者认为是Wx+b具有更加一致和非稀疏的分布。
• 但是一样研究证明放后面效果也不错。。。所以，还是看效果，虽然主流还是放前面。

下面是残差网络的实现：

from keras import layers
from keras.models import Model

def _after_conv(in_tensor):
   norm = layers.BatchNormalization()(in_tensor)
   return layers.Activation('relu')(norm)

def conv1(in_tensor, filters):
   conv = layers.Conv2D(filters, kernel_size=1, strides=1)(in_tensor)
   return _after_conv(conv)

def conv1_downsample(in_tensor, filters):
   conv = layers.Conv2D(filters, kernel_size=1, strides=2)(in_tensor)
   return _after_conv(conv)

def conv3(in_tensor, filters):
   conv = layers.Conv2D(filters, kernel_size=3, strides=1, padding='same')(in_tensor)
   return _after_conv(conv)

def conv3_downsample(in_tensor, filters):
   conv = layers.Conv2D(filters, kernel_size=3, strides=2, padding='same')(in_tensor)
   return _after_conv(conv)

def resnet_block_wo_bottlneck(in_tensor, filters, downsample=False):
   if downsample:
       conv1_rb = conv3_downsample(in_tensor, filters)
   else:
       conv1_rb = conv3(in_tensor, filters)
   conv2_rb = conv3(conv1_rb, filters)

   if downsample:
       in_tensor = conv1_downsample(in_tensor, filters)
   result = layers.Add()([conv2_rb, in_tensor])

   return layers.Activation('relu')(result)

def resnet_block_w_bottlneck(in_tensor,
                            filters,
                            downsample=False,
                            change_channels=False):
   if downsample:
       conv1_rb = conv1_downsample(in_tensor, int(filters/4))
   else:
       conv1_rb = conv1(in_tensor, int(filters/4))
   conv2_rb = conv3(conv1_rb, int(filters/4))
   conv3_rb = conv1(conv2_rb, filters)

   if downsample:
       in_tensor = conv1_downsample(in_tensor, filters)
   elif change_channels:
       in_tensor = conv1(in_tensor, filters)
   result = layers.Add()([conv3_rb, in_tensor])

   return result

def _pre_res_blocks(in_tensor):
   conv = layers.Conv2D(64, 7, strides=2, padding='same')(in_tensor)
   conv = _after_conv(conv)
   pool = layers.MaxPool2D(3, 2, padding='same')(conv)
   return pool

def _post_res_blocks(in_tensor, n_classes):
   pool = layers.GlobalAvgPool2D()(in_tensor)
   preds = layers.Dense(n_classes, activation='softmax')(pool)
   return preds

def convx_wo_bottleneck(in_tensor, filters, n_times, downsample_1=False):
   res = in_tensor
   for i in range(n_times):
       if i == 0:
           res = resnet_block_wo_bottlneck(res, filters, downsample_1)
       else:
           res = resnet_block_wo_bottlneck(res, filters)
   return res

def convx_w_bottleneck(in_tensor, filters, n_times, downsample_1=False):
   res = in_tensor
   for i in range(n_times):
       if i == 0:
           res = resnet_block_w_bottlneck(res, filters, downsample_1, not downsample_1)
       else:
           res = resnet_block_w_bottlneck(res, filters)
   return res

def _resnet(in_shape=(224,224,3),
           n_classes=1000,
           opt='sgd',
           convx=[64, 128, 256, 512],
           n_convx=[2, 2, 2, 2],
           convx_fn=convx_wo_bottleneck):
   in_layer = layers.Input(in_shape)

   downsampled = _pre_res_blocks(in_layer)

   conv2x = convx_fn(downsampled, convx[0], n_convx[0])
   conv3x = convx_fn(conv2x, convx[1], n_convx[1], True)
   conv4x = convx_fn(conv3x, convx[2], n_convx[2], True)
   conv5x = convx_fn(conv4x, convx[3], n_convx[3], True)

   preds = _post_res_blocks(conv5x, n_classes)

   model = Model(in_layer, preds)
   model.compile(loss="categorical_crossentropy", optimizer=opt,
               metrics=["accuracy"])
   return model

def resnet18(in_shape=(224,224,3), n_classes=1000, opt='sgd'):
   return _resnet(in_shape, n_classes, opt)

def resnet34(in_shape=(224,224,3), n_classes=1000, opt='sgd'):
   return _resnet(in_shape,
                 n_classes,
                 opt,
                 n_convx=[3, 4, 6, 3])

def resnet50(in_shape=(224,224,3), n_classes=1000, opt='sgd'):
   return _resnet(in_shape,
                 n_classes,
                 opt,
                 [256, 512, 1024, 2048],
                 [3, 4, 6, 3],
                 convx_w_bottleneck)

def resnet101(in_shape=(224,224,3), n_classes=1000, opt='sgd'):
   return _resnet(in_shape,
                 n_classes,
                 opt,
                 [256, 512, 1024, 2048],
                 [3, 4, 23, 3],
                 convx_w_bottleneck)

def resnet152(in_shape=(224,224,3), n_classes=1000, opt='sgd'):
   return _resnet(in_shape,
                 n_classes,
                 opt,
                 [256, 512, 1024, 2048],
                 [3, 8, 36, 3],
                 convx_w_bottleneck)

if __name__ == '__main__':
   model = resnet50()
   print(model.summary())
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142

卷积操作时必须同时考虑通道和区域吗？– DepthWise操作

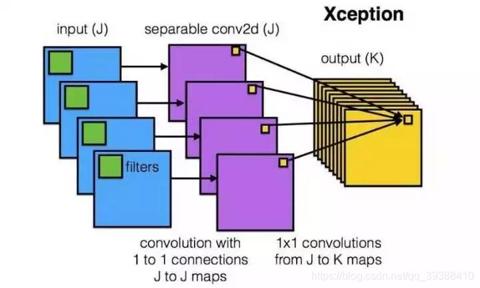
DW：首先对每一个通道进行各自的卷积操作，有多少个通道就有多少个过滤器。得到新的通道feature maps之后，这时再对这批新的通道feature maps进行标准的1×1跨通道卷积操作。
如果直接一个3×3×256的卷积核，参数量为：3×3×3×256（通道数为3，输出为256），DW的参数量为：3×3×3 + 3×1×1×256，又再次大大减少了参数量。快。

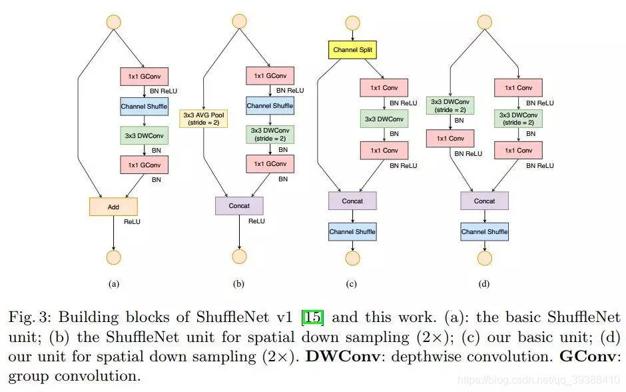
分组卷积能否对通道进行随机分组？– ShuffleNet
上图是shufflenet v1和v2的示意图，与前一个的DepthWise一样其实都是为了减少网络功耗，加快网络性能的方法。一般来说分组卷积的组别是固定的，即特征的通道被平均分到不同组里面，只到了最后才再通过两个全连接层来融合特征，作者认为这会减少模型的泛化能力。所以shufflenet会多一个channel shuffle操作，重新洗牌通道和特征。在加上和moblienet一样的可分离卷积，尽可能大的提升网络性能。
另外作者认为高效CNN网络设计应该注意的点：

• 当输入、输出channels数目相同时，conv计算所需的MAC(memory access cost)最为节省。
• 过多的Group convolution会加大MAC开销。
• 网络结构整体的碎片化会减少其可并行优化的程序。
• Element-wise操作会消耗较多的时间，不可小视。
  

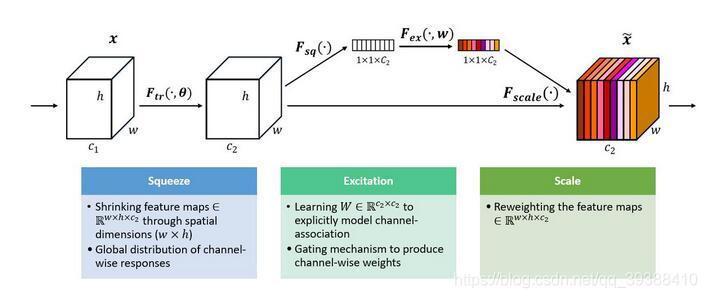
通道间的特征都是平等的吗？ – SEnet
一般网络中往往都是默认所有的通道都是独立的，平等的，也自然没有加入任何的权重，但它们为什么非要平等呢？上图是ImageNet 2017 竞赛 Image Classification 任务的冠军方案SEnet。整个模型是以squeeze-and-excitation为核心， Squeeze 是顺着空间维度来进行特征压缩，它将每个二维的特征通道变成一个实数；Excitation 是一个类似于循环神经网络中门的机制，通过参数 w 来为每个特征通道生成权重。即将Excitation 的输出的权重看做是进过特征选择后的每个特征通道的重要性，然后通过乘法逐通道加权到先前的特征上，完成在通道维度上的对原始特征的重标定。

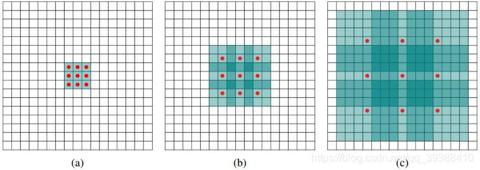
能否让固定大小的卷积核看到更大范围的区域？– Dilated convolution
空洞卷积如上图，卷积核大小依然是3×3，但是每个卷积点之间有1个空洞，也就是在绿色7×7区域里面，只有9个红色点位置作了卷积处理，其余点权重为0。这样即使卷积核大小不变，不做pooling损失信息的情况下，加大了感受野（如果加大卷积核则会增加参数），使它看到的区域变得更大了。
paper: https://arxiv.org/abs/1511.07122v3

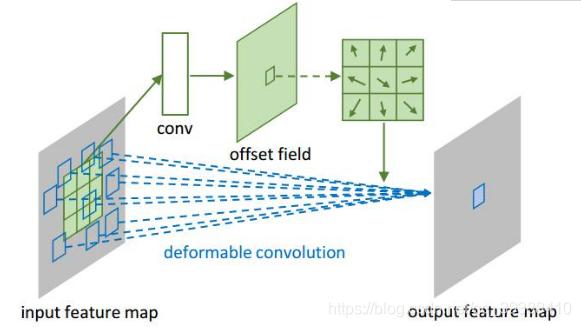
卷积核形状一定是矩形吗？– Deformable convolution 可变形卷积核
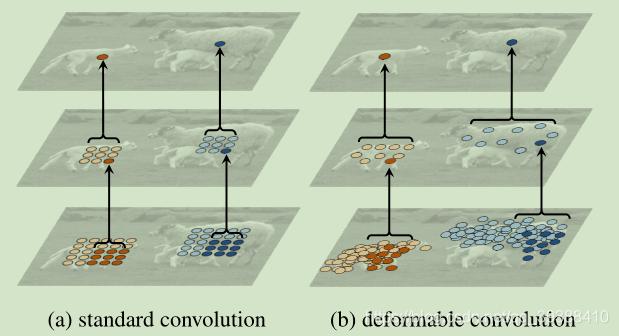
既然空洞卷积可以放缩卷积核大小了，那是否可以变形？不再是以往的矩形状？示意图如上。图中矩形的箭头是值偏移量，通过学习偏移来达到变形卷积核的目的。故模型会直接在原来的过滤器前面再加一层过滤器，这层过滤器学习的是下一层卷积核的位置偏移量（offset）。变形的卷积核能让它只看感兴趣的图像区域 ，这样识别出来的特征更佳。效果对比如下图。

卷积前后有因果关系怎么办？–causal convolution 因果卷积

神经网络可视化Crad-CAM：https:arxiv.org/pdf/1610.02391.pdf

参数过多怎么办？
由于模型的参数往往很多，需要的算力比较大，由此也衍生了一个研究热点：模型压缩。
另外现在有很多需要在嵌入式设备搭载的深度学习模型，需要更加轻量化的结构，但是深度学习模型参数很多，存在冗余，但这个冗余又是如此的必要：深度学习往往解决的是一个很复杂的非凸优化的问题，参数上的冗余保证了网络能够收敛到比较好的最优值。但是办法还是有的：

• 知识蒸馏
• 紧凑的网络设计。一般现有的网络，深度和宽度上都很大，于是出现了如SqueezeNet、MobileNet等模型的设计，使用更加细致、高效的模型设计来尝试解决。
• 卷积核的重要性和剪枝。另外还可以对卷积核的对权重更新进行诱导，使其更加稀疏，对于稀疏矩阵，可以使用更加紧致的存储方式，如CSC
• 低秩近似。也叫Low-rank分解，将稠密矩阵变成若干低秩小矩阵的近似。
• 未加限制的剪枝。对于已训练好的模型网络，可以寻找一种有效的评判手段，将不重要的connection或者filter进行裁剪来减少模型的冗余。
• 参数量化。使用聚类中心的权重代替原有权重或使用哈希
• 二值网络。参数量化的极端情况，直接二值化权重。

主要参考：
bengio deep learning
深度思考·DeepThinking
Faisal Shahbaz Five Powerful CNN Architectures