推荐|【PCL自学：Feature7】基于转动惯量和偏心量的描述符 (持续更新)

一、基于转动惯量和偏心度的描述符介绍

在这篇文章中，我们将学习如何使用pcl:: momenttofinertiaestimate类来获得基于转动惯量和偏心度的描述符。这个类还允许提取点云的轴对齐和定向的边界框(不一定是最小边框)。

【理论基础】：
特征提取方法的思想如下:
首先计算点云的协方差矩阵，提取点云的特征值和向量（可以理解特征向量就是整篇点云的主轴方向，特征值是在特征向量上的伸缩量）。可以认为合成的特征向量是标准化的，总是形成右手坐标系(主特征向量代表x轴，次特征向量代表z轴)。
然后进行迭代过程。在每次迭代中，主特征向量被旋转。旋转顺序总是相同的，并围绕其他特征向量执行，这提供了点云旋转的不变性。今后，我们将把这个旋转后的主矢量称为当前轴。
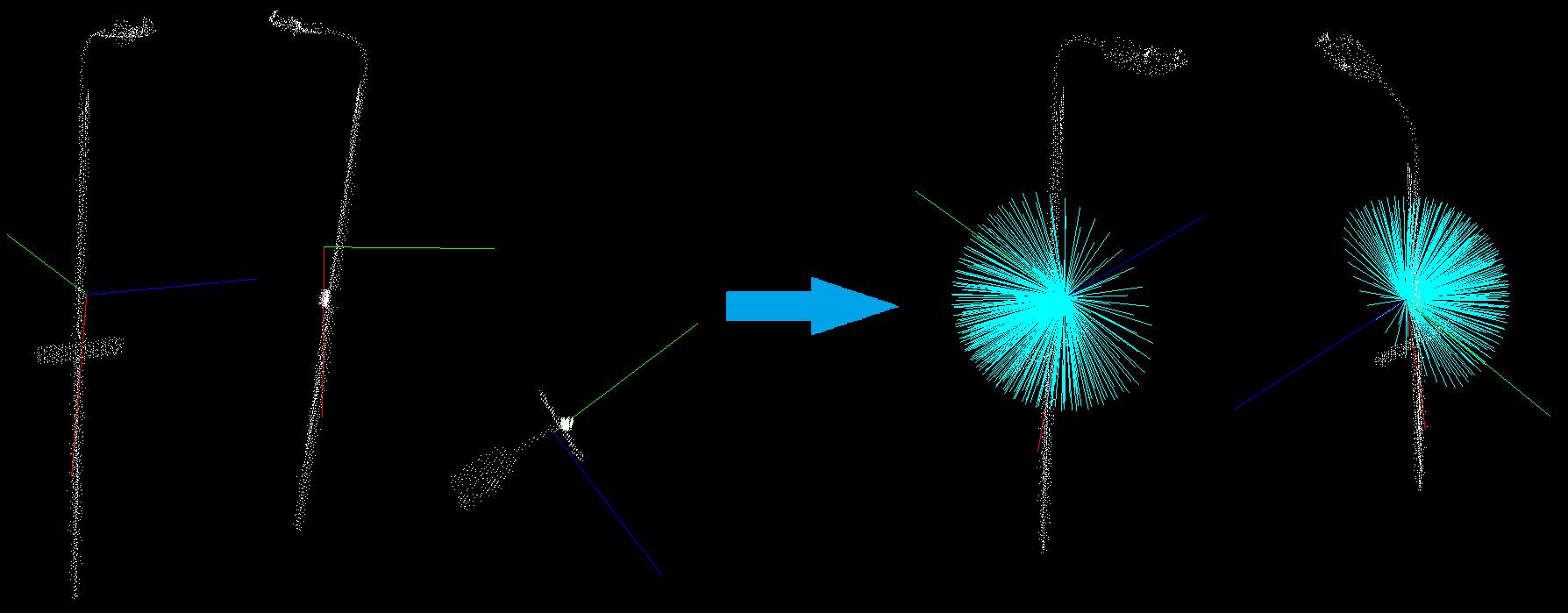
在这里插入图片描述
计算每次当前轴的转动惯量并利用当前轴进行偏心距计算。由于这个原因，当前轴矢量方向被视为平面的法向量，输入的点云可以投影到它上面。然后计算得到的投影的离心率。

PCL的momenttofinertiaestimate类还提供了获取AABB和OBB包围盒的方法。定向包围盒计算为沿着特征向量的AABB。

AABB：Axis-Aligned Bounding Box，轴对齐包围盒;
OBB：Oriented Bounding Box，有向包围盒；
OBB比包围球和AABB更加逼近物体，能显著减少包围体的个数
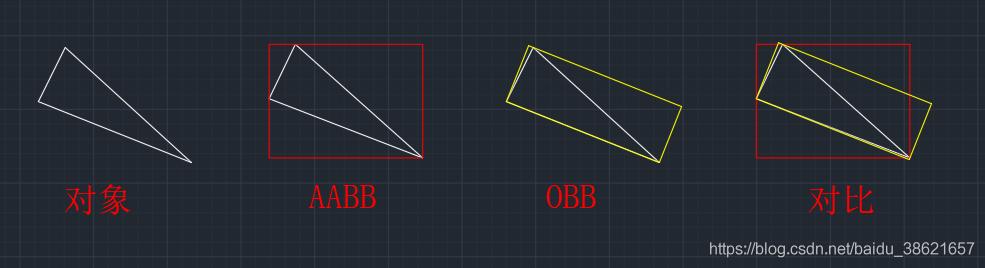
在这里插入图片描述
如下图所示黄色为AABB，红色为OBB。

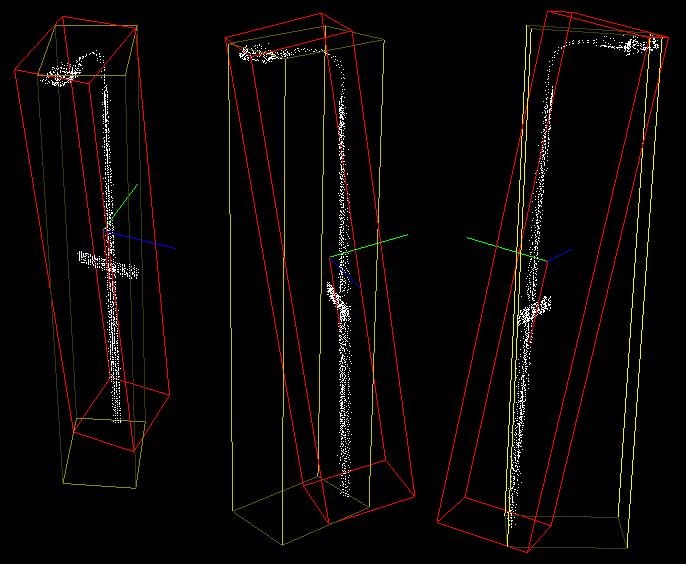
二、基于转动惯量和偏心度的描述符示例程序分析

开始之前，需要在github上下载示例的点云文件，点击这里可以下载。接下来在VS编辑器中创建一个文件moment_of_inertia.cpp，并在其中复制以下代码。

#include 
#include 
 
#include 
 #include 
 #include 
 #include 
 
 using namespace std::chrono_literals;

int main (int argc, char** argv)
{
  if (argc != 2)
    return (0);

  pcl::PointCloud<pcl::PointXYZ>::Ptr cloud (new pcl::PointCloud<pcl::PointXYZ> ());
  if (pcl::io::loadPCDFile (argv[1], *cloud) == -1)
    return (-1);

  pcl::MomentOfInertiaEstimation <pcl::PointXYZ> feature_extractor;
  feature_extractor.setInputCloud (cloud);
  feature_extractor.compute ();

  std::vector <float> moment_of_inertia;// 转动惯量
  std::vector <float> eccentricity;     // 偏心量
  pcl::PointXYZ min_point_AABB;
  pcl::PointXYZ max_point_AABB;
  pcl::PointXYZ min_point_OBB;
  pcl::PointXYZ max_point_OBB;
  pcl::PointXYZ position_OBB;
  Eigen::Matrix3f rotational_matrix_OBB;
  float major_value, middle_value, minor_value;
  Eigen::Vector3f major_vector, middle_vector, minor_vector;
  Eigen::Vector3f mass_center;

  feature_extractor.getMomentOfInertia (moment_of_inertia);
  feature_extractor.getEccentricity (eccentricity);
  feature_extractor.getAABB (min_point_AABB, max_point_AABB);
  feature_extractor.getOBB (min_point_OBB, max_point_OBB, position_OBB, rotational_matrix_OBB);
  feature_extractor.getEigenValues (major_value, middle_value, minor_value);
  feature_extractor.getEigenVectors (major_vector, middle_vector, minor_vector);
  feature_extractor.getMassCenter (mass_center);

  pcl::visualization::PCLVisualizer::Ptr viewer (new pcl::visualization::PCLVisualizer ("3D Viewer"));
  viewer->setBackgroundColor (0, 0, 0);
  viewer->addCoordinateSystem (1.0);
  viewer->initCameraParameters ();
  viewer->addPointCloud<pcl::PointXYZ> (cloud, "sample cloud");
  viewer->addCube (min_point_AABB.x, max_point_AABB.x, min_point_AABB.y, max_point_AABB.y, min_point_AABB.z, max_point_AABB.z, 1.0, 1.0, 0.0, "AABB");
  viewer->setShapeRenderingProperties(pcl::visualization::PCL_VISUALIZER_REPRESENTATION, pcl::visualization::PCL_VISUALIZER_REPRESENTATION_WIREFRAME, "AABB");

  Eigen::Vector3f position (position_OBB.x, position_OBB.y, position_OBB.z);
  Eigen::Quaternionf quat (rotational_matrix_OBB);
  viewer->addCube (position, quat, max_point_OBB.x - min_point_OBB.x, max_point_OBB.y - min_point_OBB.y, max_point_OBB.z - min_point_OBB.z, "OBB");
  viewer->setShapeRenderingProperties(pcl::visualization::PCL_VISUALIZER_REPRESENTATION, pcl::visualization::PCL_VISUALIZER_REPRESENTATION_WIREFRAME, "OBB");

  pcl::PointXYZ center (mass_center (0), mass_center (1), mass_center (2));
  pcl::PointXYZ x_axis (major_vector (0) + mass_center (0), major_vector (1) + mass_center (1), major_vector (2) + mass_center (2));
  pcl::PointXYZ y_axis (middle_vector (0) + mass_center (0), middle_vector (1) + mass_center (1), middle_vector (2) + mass_center (2));
  pcl::PointXYZ z_axis (minor_vector (0) + mass_center (0), minor_vector (1) + mass_center (1), minor_vector (2) + mass_center (2));
  viewer->addLine (center, x_axis, 1.0f, 0.0f, 0.0f, "major eigen vector");
  viewer->addLine (center, y_axis, 0.0f, 1.0f, 0.0f, "middle eigen vector");
  viewer->addLine (center, z_axis, 0.0f, 0.0f, 1.0f, "minor eigen vector");

  while(!viewer->wasStopped())
  {
    viewer->spinOnce (100);
    std::this_thread::sleep_for(100ms);
  }

  return (0);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72

【代码分析】：
现在让我们研究一下这段代码的目的是什么。前几行将被省略，因为它们很容易理解。

以下语句声明所有需要存储的描述符和边界框的相关变量。

  std::vector <float> moment_of_inertia; // 转动惯量
  std::vector <float> eccentricity;      // 离心率
  pcl::PointXYZ min_point_AABB;          //AABB盒子最小点位置
  pcl::PointXYZ max_point_AABB;          //AABB盒子最大点未位置
  pcl::PointXYZ min_point_OBB;			 //OBB盒子最小点未位置
  pcl::PointXYZ max_point_OBB;  		 //OBB盒子最大点未位置
  pcl::PointXYZ position_OBB;            //OBB盒子中心位置
  Eigen::Matrix3f rotational_matrix_OBB; //OBB盒子旋转矩阵
  float major_value, middle_value, minor_value;
  Eigen::Vector3f major_vector, middle_vector, minor_vector;
  Eigen::Vector3f mass_center;           //块中心
 
1
2
3
4
5
6
7
8
9
10
11
12

以下语句说明了如何获取描述符的计算结果

 feature_extractor.getMomentOfInertia (moment_of_inertia);
  feature_extractor.getEccentricity (eccentricity);
  feature_extractor.getAABB (min_point_AABB, max_point_AABB);
  feature_extractor.getOBB (min_point_OBB, max_point_OBB, position_OBB, rotational_matrix_OBB);
  feature_extractor.getEigenValues (major_value, middle_value, minor_value);
  feature_extractor.getEigenVectors (major_vector, middle_vector, minor_vector);
  feature_extractor.getMassCenter (mass_center);
1
2
3
4
5
6
7

以下语句使用PCLVisualizer类将结果进行了可视化，使用线框显示立方体（默认使用实体立方体，这里用线框显示更清晰）。

OBB的可视化稍微复杂一点。首先从旋转矩阵创建一个四元数，设置obb的位置，并将其传递给可视化器。

  pcl::PointXYZ center (mass_center (0), mass_center (1), mass_center (2));
  pcl::PointXYZ x_axis (major_vector (0) + mass_center (0), major_vector (1) + mass_center (1), major_vector (2) + mass_center (2));
  pcl::PointXYZ y_axis (middle_vector (0) + mass_center (0), middle_vector (1) + mass_center (1), middle_vector (2) + mass_center (2));
  pcl::PointXYZ z_axis (minor_vector (0) + mass_center (0), minor_vector (1) + mass_center (1), minor_vector (2) + mass_center (2));
  viewer->addLine (center, x_axis, 1.0f, 0.0f, 0.0f, "major eigen vector");
  viewer->addLine (center, y_axis, 0.0f, 1.0f, 0.0f, "middle eigen vector");
  viewer->addLine (center, z_axis, 0.0f, 0.0f, 1.0f, "minor eigen vector");
1
2
3
4
5
6
7

总结：
这篇文章主要介绍了基于转动惯量和偏心量的描述符，并分析了示例程序以学习如何使用该类，我们所要掌握的内容是，当需要对点云画出边界盒时，可以采用这种方式。下篇文章将会介绍RoPs旋转投影特征。

【博主简介】
斯坦福的兔子，男，天津大学机械工程工学硕士。毕业至今从事光学三维成像及点云处理相关工作。因工作中使用的三维处理库为公司内部库，不具有普遍适用性，遂自学开源PCL库及其相关数学知识以备使用。谨此将自学过程与君共享。
博主才疏学浅，尚不具有指导能力，如有问题还请各位在评论处留言供大家共同讨论。
若前辈们有工作机会介绍欢迎私信。

id="article_content" class="article_content clearfix"> id="content_views" class="htmledit_views">

博主介绍：黄菊华老师《Vue.js入门与商城开发实战》《微信小程序商城开发》图书作者，CSDN博客专家，在线教育专家，CSDN钻石讲师；专注大学生毕业设计教育、辅导。
所有项目都配有从入门到精通的基础知识视频课程，学习后应对毕业设计答辩，提供核心代码讲解，答辩指导。
项目配有对应开发文档、开题报告、任务书、PPT等，提供毕业设计论文辅导。

项目都录了发布和功能操作演示视频；项目的界面和功能都可以定制，包安装运行！！！

如果需要联系我，可以在CSDN网站查询黄菊华老师的，在文章末尾可以获取联系方式

开发技术

开发环境：JDK1.8 + Tomcat8+
开发语言：Java
开发框架：springboot
模板引擎：Thymeleaf
开发工具：Idea2022
数据库：mysql8
数据库管理工具：navicat
其他开发语言：html + css +javascript

功能清单

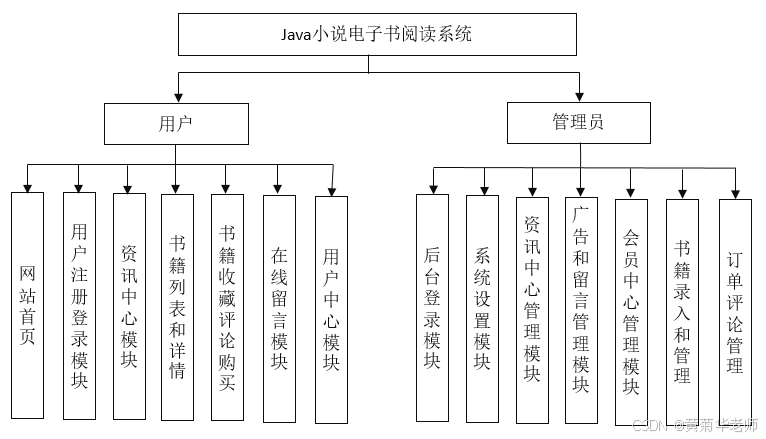
【后台功能】
系统设置：设置关于我们、联系我们、加入我们、法律声明
广告管理：设置小程序首页轮播图广告和链接
留言列表：所有用户留言信息列表，支持删除
会员列表：查看所有注册会员信息，支持删除
资讯分类：录入、修改、查看、删除资讯分类
录入资讯：录入资讯标题、内容等信息
管理资讯：查看已录入资讯列表，支持删除和修改
资讯评论列表：所有用户的评论信息列表
资讯评论管理：支持对评论信息审核，删除；审核后的信息用户才可见

图书分类设置：设置有哪些科目类型
录入图书：录入图书标题、选择分类、图书价格、上传图片、图书详细介绍
图书管理：列出所有图书信息、支持修改、删除
热门图书关键字：设置网站可以查询的热门图书关键字
图书目录管理：设置图书章节和对应内容，支持修改

图书订单列表：列出网站用户下单的所有订单信息
图书订单管理：支持删除操作
图书评论列表：列出用户对网站电影的评论信息
图书评论管理：支持修改审核操作、删除操作

【用户功能】
用户注册：填写手机账号和密码，注册新用户
登录功能：注册普通账号登录；登录后可以修改用户的基本信息，也可以退出。
关于我们：关于我们、联系我们、加入我们、法律声明
轮播广告：后台设置首页轮播广告图，可以连接到广告页面。
留言反馈：用户填写李哭咽的主题、联系人、电话、邮箱、留言内容；后台管理可以查看留言列表，可以删除留言。

图书列表：显示网站提供的所有图书信息；可以按图书的分类筛选。
图书查询：网站顶部可以输入图书关键字查询
图书详情：图书的介绍信息，包含封面，价格，介绍等
图书购买：在图书详情页面，点击“我要购买课程”，确认购买。
图书收藏：在图书详情页面，登录的用户，可以对当前图书进行收藏，收藏后的图书列表在用户中心可以查看，可以进行删除。
图书评论：在图书详情页面，登录的用户，可以填写评论内容，提交评论信息；提交的评论信息需要后台管理员审核后可见。
图书阅读：在线电子书阅读

我的图书列表：列出用户的所有购买的图书课程，可以点击图书课程名称，进入图书学习页面在线学习。
图书浏览、收藏、评论：列出用户浏览过的网站上的图书课程信息浏览记录；收藏过的图书课程信息列表，支持删除；评论过的信息列表和状态。
资讯浏览、收藏、评论：列出用户浏览过的网站上的资讯信息浏览记录；收藏过的资讯信息列表，支持删除；评论过的资讯信息列表和状态。

用户信息：姓名、联系方式、邮箱、头像、简介、介绍等，支持随时修改；用户注册的信息后台管理员可见；后台管理员可以删除。
密码修改：修改注册的密码。
退出登录：清除登录的cookie，返回到首页。