参考引用
1. RANSAC 概念及作用
-
RANSAC(Random Sample Consensus,随机采样一致性)是一种迭代方法,作用:从包含异常值的一组数据中估计数学模型的参数,RANSAC 算法假定要查看的所有数据均由内部值和异常值组成,可以用带有一组特定参数值的模型来解释离群值,而离群值在任何情况下都不适合该模型,其过程可以从数据中估计所选模型的最佳参数
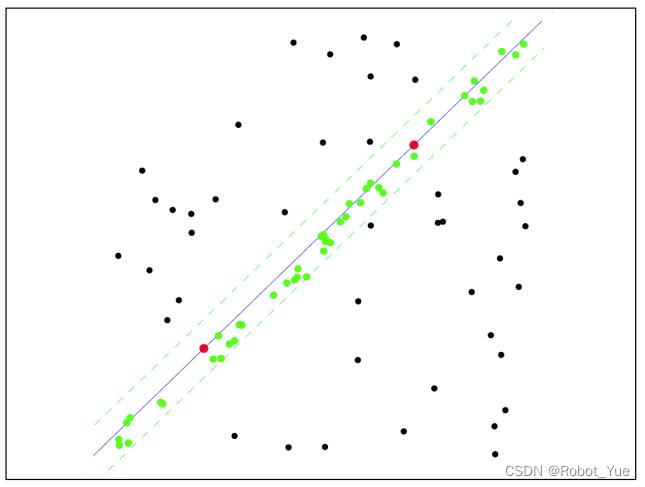
- 下面的左图和右图显示了 RANSAC 算法在二维数据集上的应用:左图是包含内部值和异常值的数据集的可视表示,右图以红色显示所有异常值,蓝色显示内部值,蓝线是 RANSAC 完成的工作结果
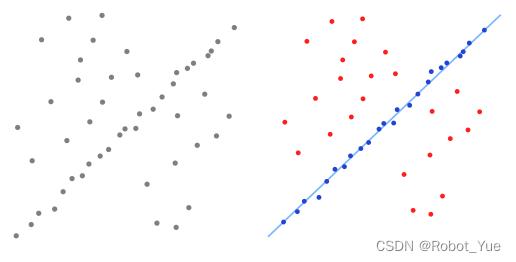
- 下面的左图和右图显示了 RANSAC 算法在二维数据集上的应用:左图是包含内部值和异常值的数据集的可视表示,右图以红色显示所有异常值,蓝色显示内部值,蓝线是 RANSAC 完成的工作结果
-
PCL 中以 RANSAC 算法为核心,实现了五种类似于 RANSAC 的随机参数估计算法,例如:随机采样一致性估计(RANSAC) 、最大似然一致性估计(MLESAC)、最小中值方差一致性估计(LMEDS)等,所有的估计参数算法都符合一致性准则
- 利用 RANSAC 可实现点云分割,PCL 中支持的几何模型分割有空间平面、直线、二维或三维圆、圆球、锥体等
- RANSAC 的另一应用就是点云配准对的剔除
2. RANSAC 算法简介
(1)RANSAC 从样本中随机抽选出一个样本子集,使用最小方差估计算法对这个子集计算模型参数,然后计算所有样本与该模型的偏差,再使用一个预先设定好的阈值与偏差比较,当偏差小于阈值时,该样本点属于模型内样本点(inliers),或称内部点、局内点或内点,否则为模型外样本点(outliers),或称外部点、局外点或外点,同时记录下当前的 inliers 的个数,然后重复这一过程
(2)每一次重复都记录当前最佳模型参数,所谓最佳即是 inliers 个数最多,对应的 inliers 个数为 best_ninliers
(3)每次迭代的末尾都会根据期望的误差率、best_ninliers、总样本个数、当前迭代次数,计算一个迭代结束评判因子,据此决定是否迭代结束,迭代结束后,最佳模型参数就是最终的模型参数估计值
- 换而言之,RANSAC 算法是从一组含有 “外点”(outliers) 的数据中正确估计数学模型参数的迭代算法。“外点” 一般指的数据中的噪声,比如说:匹配中的误匹配和估计曲线中的离群点,最多可处理 50% 的外点情况
- 所以,RANSAC 也是一种 “外点” 检测算法,RANSAC 算法是一种不确定算法,它只能在一种概率下产生结果,并且这个概率会随着迭代次数的增加而加大。对于 RANSAC 算法来说,一个基本的假设就是数据是由 “内点” 和 “外点” 组成的,“内点” 就是组成模型参数的数据,“外点” 就是不适合模型的数据
3. RANSAC 实现流程
3.1 具体流程
-
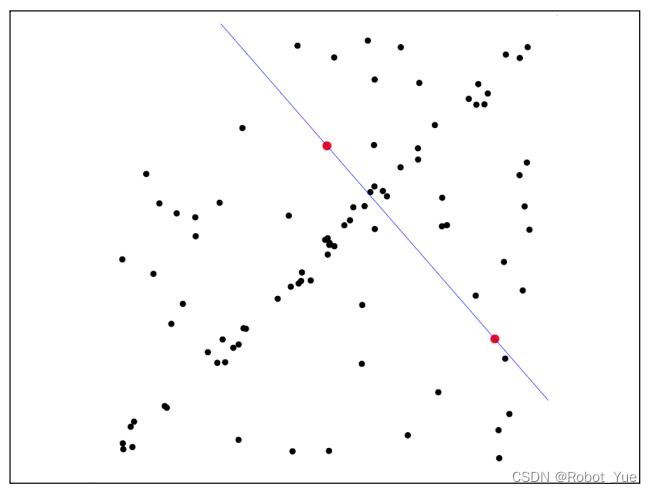
1、选定一个 sample 即对于直线模型来说只需随机选取两个点 p 0 = ( x 0 , y 0 ) , p 1 = ( x 1 , y 1 ) \mathrm{p_0}=(x_0,y_0),\mathrm{p_1}=(x_1,y_1) p0=(x0,y0),p1=(x1,y1)
-
2、求解模型(直线)方程
x 1 = x 0 + a t y 1 = y 0 + b tx1=x0+aty1=y0+btx 1 = x 0 + a t y 1 = y 0 + b t - p 0 = [ x 0 , y 0 ] T , n = [ a , b ] T \text{p}_0=[x_0,y_0]^T,\text{n}=[a,b]^T p0=[x0,y0]T,n=[a,b]T
-
Δ
x
=
x
1
−
x
0
=
a
t
,
Δ
y
=
y
1
−
y
0
=
b
t
→
Δ
x
Δ
y
=
a
b
\Delta x=x_1-x_0=at,\Delta y=y_1-y_0=bt\to\dfrac{\Delta x}{\Delta y}=\dfrac{a}{b}
Δx=x1−x0=at,Δy=y1−y0=bt→ΔyΔx=ba
- a = Δ x Δ x 2 + Δ y 2 , b = Δ y Δ x 2 + Δ y 2 a=\frac{\Delta x}{\Delta x^2+\Delta y^2},b=\frac{\Delta y}{\Delta x^2+\Delta y^2} a=Δx2+Δy2Δx,b=Δx2+Δy2Δy
-
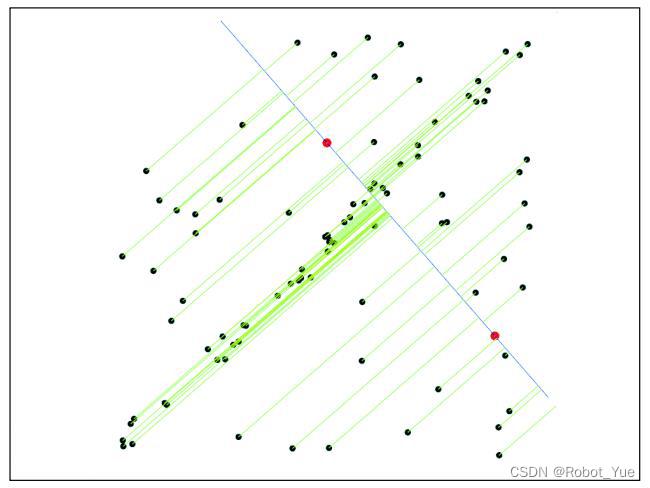
3、计算每个点 p i = ( x i , y i ) p_i=(x_i,y_i) pi=(xi,yi) 的误差函数
d i = n T ( p i − p 0 ) ∥ n ∥ 2 d_i=\dfrac{n^T(\mathrm p_i-\mathrm p_0)}{\|n\|_2} di=∥n∥2nT(pi−p0)
-
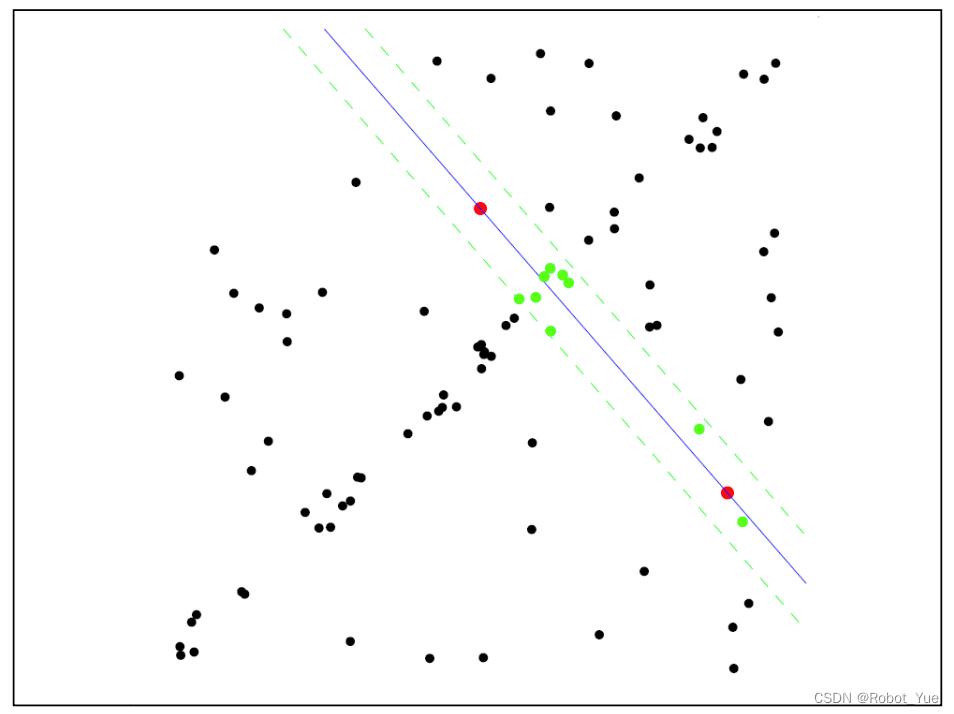
4、统计与模型(直线)一致的点,即小于设定阈值 τ \tau τ 的内点 d i d_i di(inliers)
-
5、重复上述 4 个步骤并迭代 N 次,选择拥有最多内点(inliers)的模型(直线)
3.2 两个参数选定
- 距离阈值
τ
\tau
τ
- 通常根据经验来选定(一般不用卡方分布试验来选,因为实际情况下模型标准差未知)
- 迭代次数
N
N
N
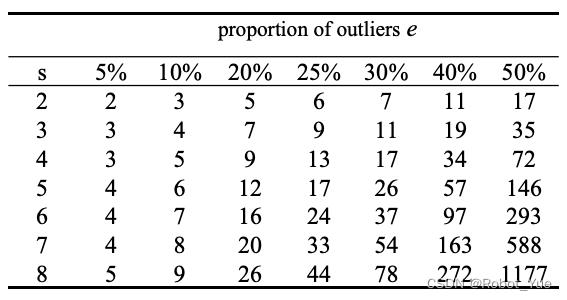
- e e e:采样点是外点的概率(见下表)
- s s s:采样点的数量(直线拟合中为 2)
- N N N:采样次数(RANSAC 迭代次数)
- p p p:至少得到一个好样本(没有外点)的置信度(人为给定,比如 0.9)
( 1 − ( 1 − e ) s ) N = 1 − p \left(1-(1-e)^s\right)^N=1-p (1−(1−e)s)N=1−p
N = l o g ( 1 − p ) l o g ( 1 − ( 1 − e ) s ) N=\dfrac{log(1-p)}{log(1-(1-e)^s)} N=log(1−(1−e)s)log(1−p)
3.3 两个实践技巧
-
找到一条达到预期的模型/直线(内点的概率达到期望值)后就可以提前终止迭代,节省计算时间
T = ( 1 − e ) ⋅ ( t o t a l n u m o f d a t a p o i n t s ) T=(1-e)·(total num of data points) T=(1−e)⋅(total num of data points) -
当最终的模型/直线选出来之后,使用 LSQ(最小二乘)法重新优化一下,所得数据更加准确
4. RANSAC 存在的问题
- RANSAC 理论上可剔除 outliers 的影响,并得到全局最优的参数估计,但存在两个问题
- 首先,在每次迭代中都要区分 inliers 和 outlieres,因此需要事先设定阈值,当模型具有明显的物理意义时,这个阈值还比较容易设定,但是若模型比较抽象时,阈值就不那么容易设定了,而且固定阈值不适用于样本动态变化的应用
- 其次,RANSAC 的迭代次数是运行期决定的,不能预知迭代的确切次数(当然迭代次数的范围是可以预测的)。除此之外,RANSAC 只能从一个特定数据集中估计一个模型,当两个(或者更多个)模型存在时,RANSAC 不能找到别的模型
5. RANSAC 代码实现(C++)
-
random_sample_consensus.cpp
#include#include #include #include #include #include #include #include #include #include // chrono_literals 是一个时间单位后缀,它可以让我们在编写 C++ 代码时更方便地定义时间常量 // 通过使用这个后缀,我们可以直接在数字后面添加特定的后缀表示不同的时间单位 // 例如:ns(纳秒)、us(微秒)、ms(毫秒)、s(秒)、min(分钟)、h(小时)、d(天)等 using namespace std::chrono_literals; // final 参数是可选的,如果它被提供,则将其作为另一个点云添加到可视化器中 pcl::visualization::PCLVisualizer::Ptr simpleVis(pcl::PointCloud<pcl::PointXYZ>::ConstPtr cloud, pcl::PointCloud<pcl::PointXYZ>::ConstPtr final = nullptr) { // 3D Viewer 表示可视化窗口的标题 pcl::visualization::PCLVisualizer::Ptr viewer(new pcl::visualization::PCLVisualizer ("3D Viewer")); viewer->addPointCloud<pcl::PointXYZ> (cloud, "sample cloud"); // 将点云数据添加到可视化器中,并命名为 "sample cloud" // 设置点云的大小为 2 viewer->setPointCloudRenderingProperties (pcl::visualization::PCL_VISUALIZER_POINT_SIZE, 2, "sample cloud"); // 将点云 final 显示为红色的点,点的大小为 4,以便进行可视化和调试 if (final != nullptr) { viewer->addPointCloud<pcl::PointXYZ> (final, "final"); // 将第二个点云数据添加到可视化器中,并命名为 "final" viewer->setPointCloudRenderingProperties (pcl::visualization::PCL_VISUALIZER_COLOR, 1.0, 0.0, 0.0, "final"); // 设置点云的颜色为红色 viewer->setPointCloudRenderingProperties (pcl::visualization::PCL_VISUALIZER_POINT_SIZE, 4, "final"); // 设置点云的大小为 4 } viewer->addCoordinateSystem (1.0, "global"); viewer->initCameraParameters (); return (viewer); } int main(int argc, char *argv[]) { // 定义并实例化两个共享的 Point Cloud 结构 pcl::PointCloud<pcl::PointXYZ>::Ptr cloud(new pcl::PointCloud<pcl::PointXYZ>); pcl::PointCloud<pcl::PointXYZ>::Ptr final(new pcl::PointCloud<pcl::PointXYZ>); // 用点填充上面其中一个 Point Cloud cloud->width = 500; cloud->height = 1; cloud->is_dense = false; cloud->points.resize(cloud->width * cloud->height); for (std::size_t i = 0; i < cloud->points.size(); ++i) { // 检查程序启动时是否有 -s 或 -sf 参数传入(分别得到不同结果,平面或球体) if (pcl::console::find_argument(argc, argv, "-s") >= 0 || pcl::console::find_argument(argc, argv, "-sf") >= 0) { cloud->points[i].x = 1024 * rand() / (RAND_MAX + 1.0); cloud->points[i].y = 1024 * rand() / (RAND_MAX + 1.0); if (i % 5 == 0) { // 可能会散落在球体外 cloud->points[i].z = 1024 * rand() / (RAND_MAX + 1.0); } else if (i % 2 == 0) { // 在球体正方向内 cloud->points[i].z = sqrt(1 - (cloud->points[i].x * cloud->points[i].x) - (cloud->points[i].y * cloud->points[i].y)); } else { // 在球体负方向内 cloud->points[i].z = -sqrt(1 - (cloud->points[i].x * cloud->points[i].x) - (cloud->points[i].y * cloud->points[i].y)); } } else { cloud->points[i].x = 1024 * rand() / (RAND_MAX + 1.0); cloud->points[i].y = 1024 * rand() / (RAND_MAX + 1.0); if (i % 2 == 0) { cloud->points[i].z = 1024 * rand() / (RAND_MAX + 1.0); } else { cloud->points[i].z = -1 * (cloud->points[i].x + cloud->points[i].y); } } } std::vector<int> inliers; // 使用 RANSAC 算法估计平面(-f)或球体(-sf)模型,并得到内点集合(inliers) pcl::SampleConsensusModelSphere<pcl::PointXYZ>::Ptr model_s(new pcl::SampleConsensusModelSphere<pcl::PointXYZ>(cloud)); pcl::SampleConsensusModelPlane<pcl::PointXYZ>::Ptr model_p(new pcl::SampleConsensusModelPlane<pcl::PointXYZ>(cloud)); if (pcl::console::find_argument(argc, argv, "-f") >= 0) { // 创建一个随机采样一致性对象,并将上面创建的模型对象作为参数传入 pcl::RandomSampleConsensus<pcl::PointXYZ> ransac(model_p); // 这个距离阈值 0.01 是用来判断一个点是否属于模型的,如果某个点与模型的 // 距离小于等于该阈值,则被认为是内点(inlier),否则被认为是外点(outlier) ransac.setDistanceThreshold(.01); // 执行随机采样一致性算法,并得到内点的索引集合(inliers) ransac.computeModel(); ransac.getInliers(inliers); } else if (pcl::console::find_argument(argc, argv, "-sf") >= 0) { pcl::RandomSampleConsensus<pcl::PointXYZ> ransac(model_s); ransac.setDistanceThreshold(.01); ransac.computeModel(); ransac.getInliers(inliers); } /* 作用:将提取原始点云中索引列表中列出的点,并将它们复制到指向 final 的目标点云中 结果点云仅包含所选的点子集,而不是整个原始点云 1.*cloud:指向包含所有点的原始点云的指针 2.inliers:一组索引,表示要从原始点云中提取的点的子集 这些索引通常来自某种过滤操作,例如:平面分割或异常值去除 3.*final:指向目标点云的指针,提取的点的子集将存储在其中 */ pcl::copyPointCloud(*cloud, inliers, *final); pcl::visualization::PCLVisualizer::Ptr viewer; if (pcl::console::find_argument(argc, argv, "-f") >= 0 || pcl::console::find_argument(argc, argv, "-sf") >= 0) { // 同时显示原始点云和计算后的点云 viewer = simpleVis(cloud, final); } else { viewer = simpleVis(cloud); // 只显示原始点云 } while (!viewer->wasStopped()) { viewer->spinOnce(100); // C++11 引入的线程库函数,其作用是使当前线程休眠一段时间 // 接受一个时间参数,可以是任何表示时间段的类型,比如 // std::chrono::milliseconds 表示毫秒,因此 100ms 表示休眠 100 毫秒 std::this_thread::sleep_for(100ms); // 调用时,当前线程将被挂起,直到过了指定的时间后再继续执行 } return 0; } - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
-
配置文件 CMakeLists.txt
cmake_minimum_required(VERSION 3.5 FATAL_ERROR) project(random_sample_consensus) set(CMAKE_CXX_STANDARD 14) # std::chrono_literals 为 C++14 标准 find_package(PCL 1.2 REQUIRED) include_directories(${PCL_INCLUDE_DIRS}) link_directories(${PCL_LIBRARY_DIRS}) add_definitions(${PCL_DEFINITIONS}) add_executable (random_sample_consensus random_sample_consensus.cpp) target_link_libraries (random_sample_consensus ${PCL_LIBRARIES})- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
-
编译并执行
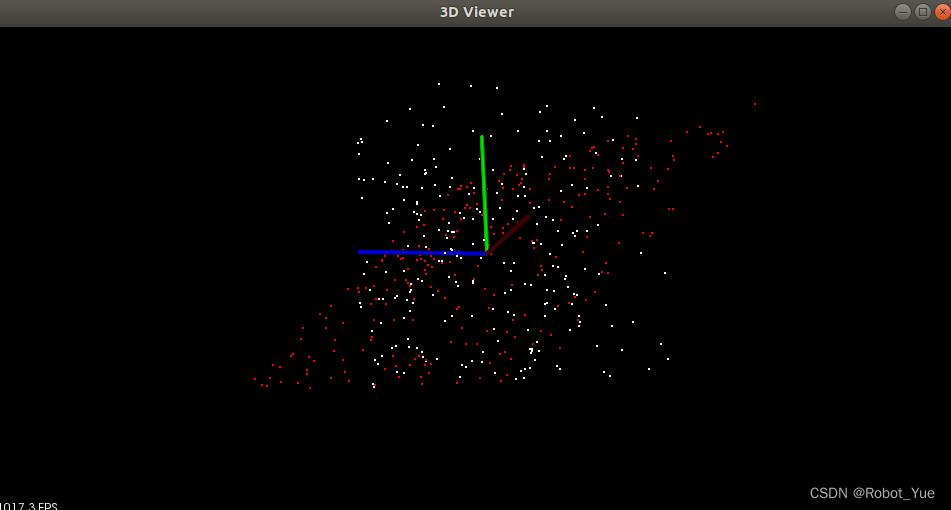
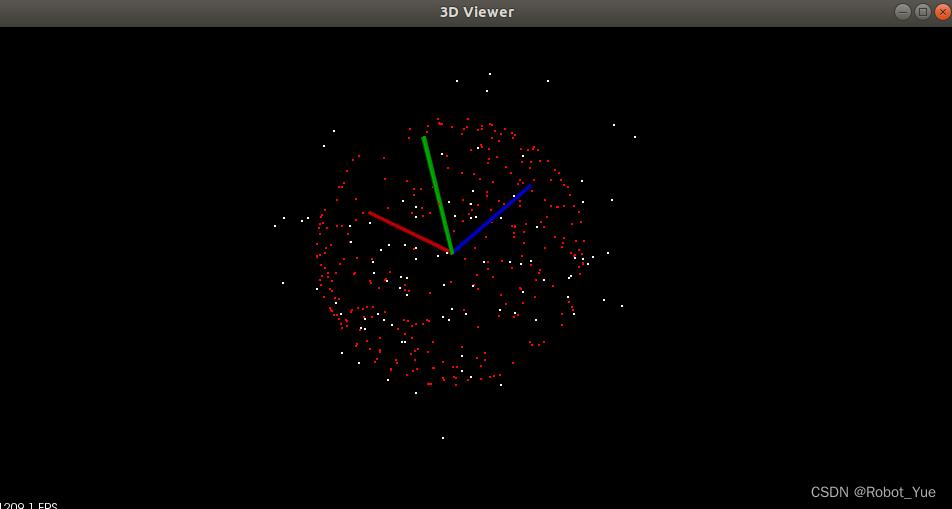
$ mkdir build $ cd build $ cmake .. $ make $ ./random_sample_consensus -f # 下图一:创建包含外部点的平面,并计算平面内部点 $ ./random_sample_consensus -sf # 下图二:创建包含外部点的球体,并计算球体内部点- 1
- 2
- 3
- 4
- 5
- 6
- 7

评论记录:
回复评论: