kd树

k-d树是一种点云划分方法，基本思路是，对方差最差的维度进行二分分割，从而得到两个子集，再对这两个子集进行相同的操作，直到所有子集的元素个数低于设定值，在opend3d中生成一个kd树的方法如下

import open3d as o3d

pcdPath = o3d.data.PCDPointCloud().path
pcd = o3d.io.read_point_cloud(pcdPath)
kdt = o3d.geometry.KDTreeFlann(pcd)

• 1
• 2
• 3
• 4
• 5

【KDtreeFlann】类，是open3d中最基础的kd树。这种数据结构，对数据索引来说十分便捷，能够将原本的$O(n^2)$复杂度降低到类似$O(\ln n)$的水平。KDTreeFlann针对索引半径、索引范围，主要提供了三种索引方式

# 通过距离和最大点数来索引
search_hybrid_vector_3d(query, radius, max_nn)
# 通过点数索引
search_knn_vector_3d(self, query, knn)
# 通过半径索引
search_radius_vector_3d(self, query, radius)
# 综合索引方法， search_param为专门为kd树提供的参数对象
search_vector_3d(self, query, search_param)

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8

对于这四种$3d$方法，都有一个与之对应的$xd$版本，可以用于更高或者更低维度的 kd-tree的索引。下图分别使用了基于点数和基于半径的方法进行索引，红色表示距离第70000号点最近的10个点；绿色表示距离70000号点距离小于0.2米的点。

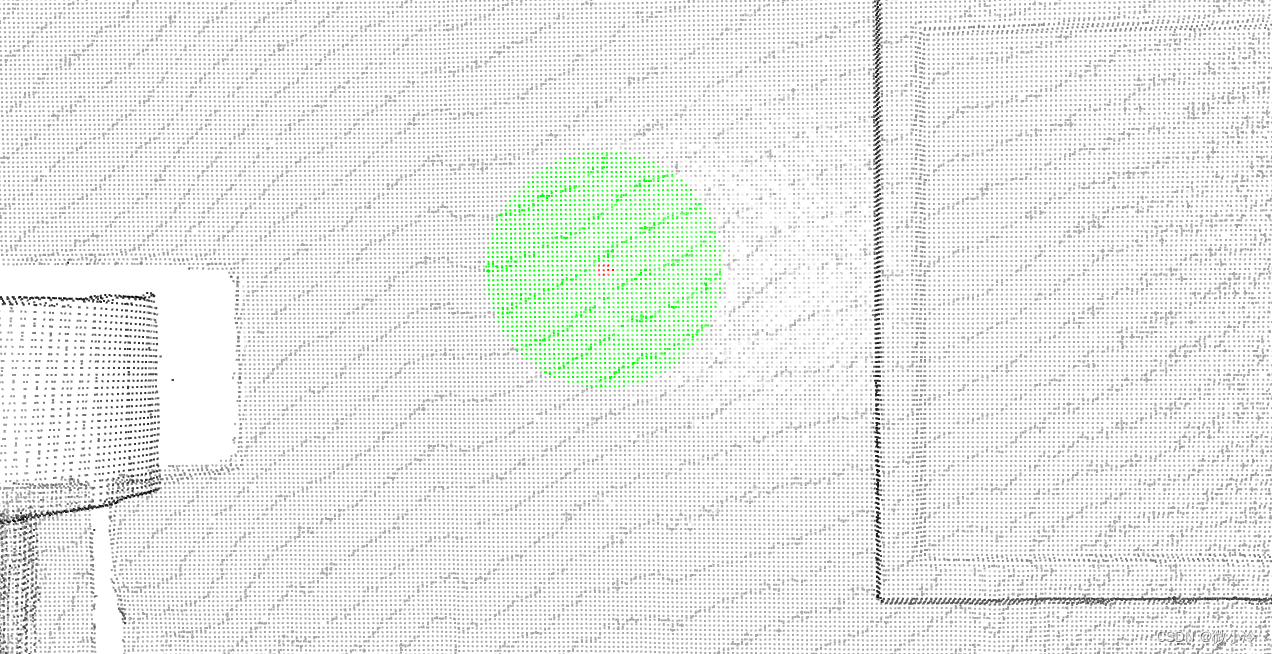
代码如下

from copy import deepcopy
kdPCD = deepcopy(pcd)
kdPCD.paint_uniform_color([0.5, 0.5, 0.5])
k, idx, _ = kdt.search_radius_vector_3d(kdPCD.points[70000], 0.2)
for i in idx: kdPCD.colors[i] = [0, 1, 0]

print(k)    # 2480

_, idx, _ = kdt.search_knn_vector_3d(kdPCD.points[70000], 10)
for i in idx: kdPCD.colors[i] = [1, 0, 0]

o3d.visualization.draw_geometries([kdPCD])

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12

八叉树

oc树是一种空间栅格化方法，其思路来自于二分法。

以一维空间举例，就是对一条线段不断地二分，得到一系列的子线段，如果子线段中包含的元素大于2，那么就继续分割，直到所有子线段中至多只有一个元素为止。

就一维而言是二分，二维空间是四分，三维空间就是八分了，故而是八叉树。

【Octree】是open3d中最简单的八叉树，其创建方法为先建立对象，再注入点云数据。

octree = o3d.geometry.Octree(max_depth=6)
octree.convert_from_point_cloud(pcd, size_expand=0.01)
o3d.visualization.draw_geometries([octree])

• 1
• 2
• 3

直观感受一下大致是这种

其中，参数max_depth可以理解为八分的最多次数。这个东西很微妙，如果不设置，当一个小区域内有大量点的时候，就会不断地分割下去，很浪费性能。size_expand是一个微小的膨胀系数，从而让每个方块把点包裹进去。

为了让这棵八叉树更加清晰，可以对点云上色

octree = o3d.geometry.Octree(max_depth=5)
octree.convert_from_point_cloud(pcd, size_expand=0.01)
o3d.visualization.draw_geometries([octree])

• 1
• 2
• 3

效果如下，有种我的世界的既视感。

除了通过点云生成八叉树，也可以通过体元生成八叉树

vxs = o3d.geometry.VoxelGrid.create_from_point_cloud(pcd, voxel_size=0.01)
octree = o3d.geometry.Octree(max_depth=6)
octree.create_from_voxel_grid(vxs)

• 1
• 2
• 3

其绘制结果和上面的图是一样的，故不再展示。

DBSCAN聚类

无论kd树还是oc树，都是通过临近点的点云分割方法，其主要目的是索引。相比之下，聚类则是十分常用的语义分割方式。

DBSCAN，即Density-Based Spatial Clustering of Applications with Noise，基于密度的噪声应用空间聚类。在DBSCAN算法中，将数据点分为三类：

1. 核心点：若样本$x_i$的$\epsilon$邻域内至少包含了$M$个点，则为核心点
2. 边界点：若样本$x_i$的$\epsilon$邻域内包含的点数小于$M$，但在其他核心点的$\epsilon$邻域内，则为边界点
3. 噪声：既非核心点也非边界点则为噪声

可见，DBSCAN算法需要两个参数，分别是邻域半径$\epsilon$和点数$M$。

令$\epsilon =0.1,M=50$，则其聚类效果如下，完美实现了语义分割。

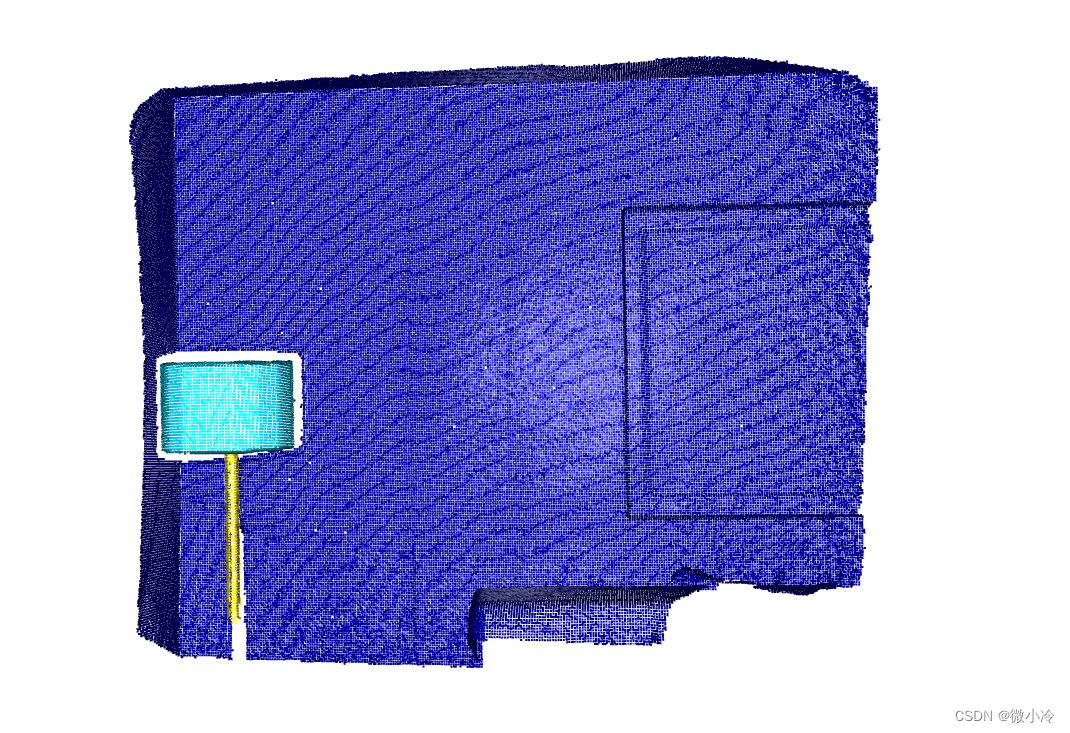
代码如下

import numpy as np
import matplotlib.pyplot as plt

pcdDB = deepcopy(pcd)
Labels = np.array(pcdDB.cluster_dbscan(0.1, 50))
print(np.max(Labels))                   # 得到结果为2
cs = plt.get_cmap("jet")(Labels/3)      # 伪彩映射
cs[labels < 0] = 0  # labels = -1 的簇为噪声，以黑色显示
pcdDB.colors = o3d.utility.Vector3dVector(cs[:, :3])
o3d.visualization.draw_geometries([pcdDB])

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10

其中，【cluster_dbscan】即为DBSCAN聚类方法，输入参数分别是$\epsilon$，表示同一聚类中最大点间距；$M$表示有效聚类的最小点数。

其聚类结果的最大值是$2$，说明分成了$0,1,2$总共三类，与图像显示的结果是一致。

RANSAC 平面分割

RANSAC，即 RANdom SAmple Consensus，随机抽样一致算法。

以平面上的点集举例，假设点集中有一条直线$L$，$L$外的点很少，均为噪声。

那么第一步，随机选取两个点连成一条直线$\hat{L}$，那么这条直线有可能就是$L$，也有可能是噪声连出来的莫名其妙的一条线。

接下来，随机抽取点集中的一些点，如果随机抽取的大部分点都落在$L$附近，那么就说明$\hat{L}$有很大的概率就是$L$；否则说明不太像是$L$。随着抽取出的直线越来越多，最后可以得到最接近$L$的直线，从而完成了对点集的分割。

【segment_plane】是open3d中基于RANSAC算法的平面分割方法，其主要输入参数为内点到平面模型的最大距离d，用于拟合平面的采样点数n，以及最大迭代次数nIter。

令$d=0.05,n=5$，最大迭代50次，其平面分割结果为

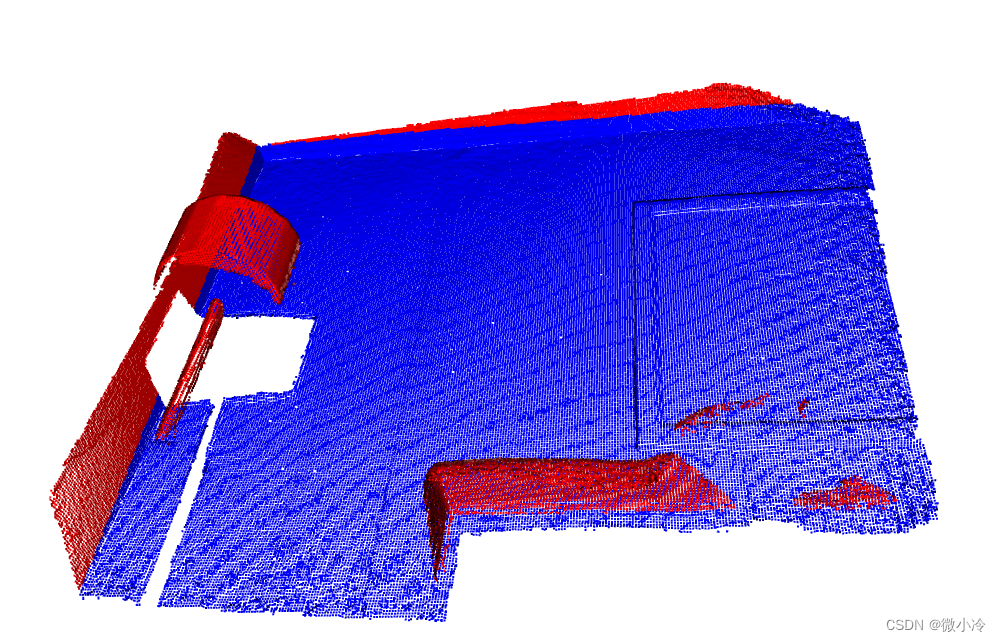
代码如下

plane, ids = pcd.segment_plane(0.05, 5, 50)

iCloud = pcd.select_by_index(ids)
iCloud.paint_uniform_color([0, 0, 1])

oCloud = pcd.select_by_index(ids, invert=True)
oCloud.paint_uniform_color([0.5, 0.5, 0.5])

o3d.visualization.draw_geometries([iCloud, oCloud])

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9

该方法有两个返回值，plane即为分割得到的平面方程的$ABCD$参数，ids即处于平面内的点。