Python-open3d点云配准

文章目录

ICP算法

ICP, 即Iterative Closest Point, 迭代点算法。

ICP算法有多种形式，其中最简单的思路就是比较点与点之间的距离，对于点云 P = { p i } , Q = { q i } P=\{p_i\}, Q=\{q_i\} P={pi​},Q={qi​}而言，如果二者是同一目标，通过旋转、平移等操作可以实现重合的话，那么只需要固定 Q Q Q而不断地旋转或平移 P P P，最终二者一定能最完美地重合。

设 R , t R, t R,t分别为旋转矩阵和平移矩阵，在完美匹配的情况下，必有 q i = R p i + t q_i = Rp_i + t qi​=Rpi​+t。但三维点云不具备栅格特征，故而很难保证 q i q_i qi​和 p i p_i pi​一一对应，所以求解问题变为优化问题，目标函数为

arg min ⁡ R , t 1 2 ∑ i = 1 n ∥ q i − R p i − t ∥ 2 \argmin_{R,t}\frac{1}{2}\sum^n_{i=1}\Vert q_i-Rp_i-t\Vert^2 R,targmin​21​i=1∑n​∥qi​−Rpi​−t∥2

1992年Chen和Medioni对此方案进行了改进，提出了点对面的预估方法，其目标函数为

arg min ⁡ R , t 1 2 ∑ i = 1 n [ ( q i − R p i ) ⋅ n p ] 2 \argmin_{R,t}\frac{1}{2}\sum^n_{i=1}[(q_i-Rp_i)\cdot n_p]^2 R,targmin​21​i=1∑n​[(qi​−Rpi​)⋅np​]2

其中 n p n_p np​是点 p p p的法线，这种方案显然效率更高。

在使用ICP算法前后，两个点云的叠加图像变化如下

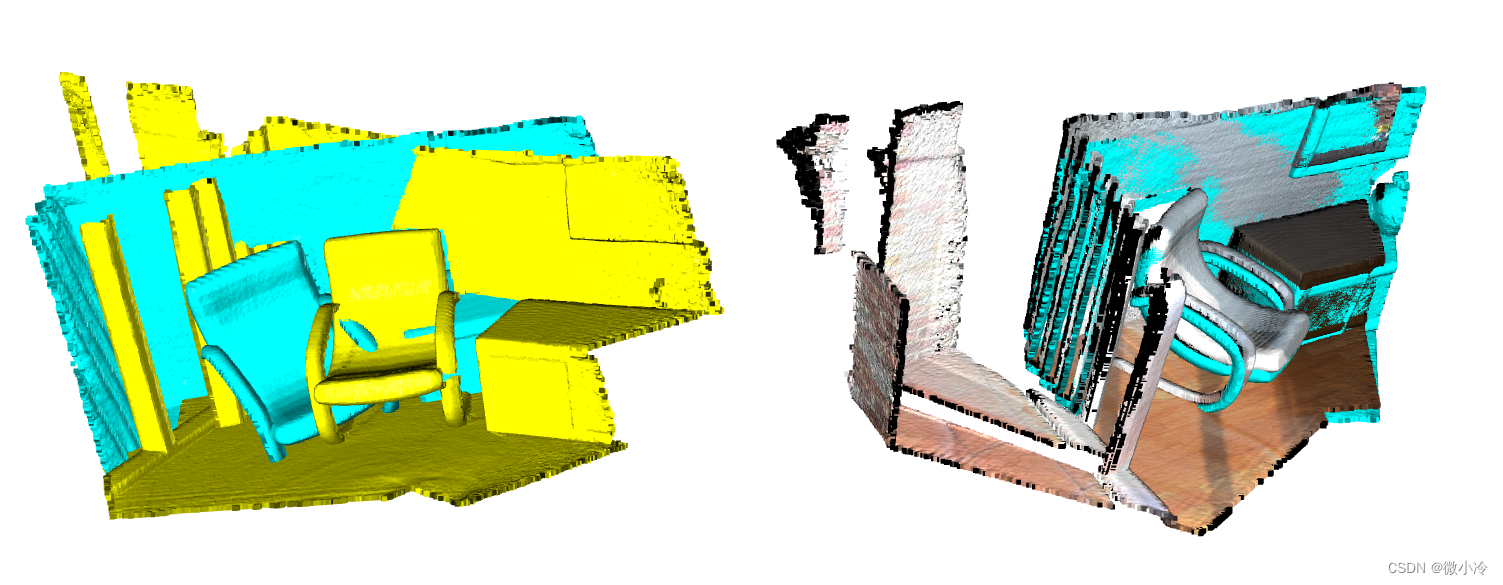
在这里插入图片描述

基于Open3d实现的代码如下

import numpy as np
import open3d as o3d

pipreg = o3d.pipelines.registration

pcd = o3d.data.DemoICPPointClouds()
src = o3d.io.read_point_cloud(pcd.paths[0])
tar = o3d.io.read_point_cloud(pcd.paths[1])
th = 0.02
trans_init = np.array([
    [0.862, 0.011, -0.507, 0.5], [-0.139, 0.967, -0.215, 0.7],
    [0.487, 0.255, 0.835, -1.4], [0.0, 0.0, 0.0, 1.0]])

reg = pipreg.registration_icp(
    src, tar, th, trans_init,
    pipreg.TransformationEstimationPointToPoint())

print(reg.transformation)   # 变换矩阵
print(reg)  # 表示点云配准的拟合程度
'''
fitness=3.724495e-01, inlier_rmse=7.760179e-03, and correspondence_set size of 74056 Access transformation to get result.
'''
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22

【registration_icp】即为open3d实现的点云配准函数，在示例中，输入的5个参数分别为点云 P P P、目标点云 Q Q Q、同名点未匹配时的最大距离、初始变化矩阵、变换方法。

【TransformationEstimationPointToPoint】即点对点的目标函数。

匹配完成后，打印的变换矩阵为

[ 0.83924644 0.01006041 − 0.54390867 0.64639961 − 0.15102344 0.96521988 − 0.21491604 0.75166079 0.52191123 0.2616952 0.81146378 − 1.50303533 0. 0. 0. 1. ] ] [0.839246440.01006041−0.543908670.64639961−0.151023440.96521988−0.214916040.751660790.521911230.26169520.81146378−1.503035330.0.0.1.]] ​0.83924644−0.151023440.521911230.​0.010060410.965219880.26169520.​−0.54390867−0.214916040.811463780.​0.646399610.75166079−1.503035331.]​ ​

绘图代码如下

from copy import deepcopy
srcDraw = deepcopy(src)
tarDraw = deepcopy(tar)
srcDraw.paint_uniform_color([1, 1, 0])
tarDraw.paint_uniform_color([0, 1, 1])

srcDrawICP = deepcopy(src)
tarDrawICP = deepcopy(tarDraw)
srcDrawICP.transform(reg.transformation)

geo = [srcDraw, tarDraw,
       srcDrawICP.translate((4.5, 0, 0)),
       tarDrawICP.translate((4.5, 0, 0))]

o3d.visualization.draw_geometries(geo)
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15

鲁棒核

现有点云 P , Q P,Q P,Q，若二者存在一一对应的点列 p i ∈ P , q i ∈ Q p_i\in P, q_i\in Q pi​∈P,qi​∈Q，通过对 Q Q Q进行矩阵变换 T T T，以期二者完全配准，那么对于第 i i i个点而言，记 r i ( T ) = ( p i − T q i ) ⋅ n p i r_i(T)=(p_i-Tq_i)\cdot n_{p_i} ri​(T)=(pi​−Tqi​)⋅npi​​， n p i n_{p_i} npi​​为点 p i p_i pi​的法向量，即 q i q_i qi​在经过矩阵变换后与 p i p_i pi​在其法向量方向的残差。

则点对面ICP的目的，就是让下面的函数取值最小

E ( T ) = ∑ i = 1 N r i ( T ) 2 E(T)=\sum_{i=1}^Nr_i(T)^2 E(T)=i=1∑N​ri​(T)2

在这个优化问题中， r i r_i ri​的作用举足轻重，任何对 r i r_i ri​的形式上的更改，都会直接影响优化结果，例如将这个优化问题改写成重复加权最小二乘法的形式

E ( T ) = ∑ i = 1 N w i r i ( T ) 2 E(T)=\sum_{i=1}^Nw_ir_i(T)^2 E(T)=i=1∑N​wi​ri​(T)2

让 r i r_i ri​乘上一个权重，那么在具体匹配的过程中，就可以降低某些特殊值的影响。如果这个权重本身就是 r i r_i ri​的函数，那么加权过程可以写成更加抽象的形式

E ( T ) = ∑ i = 1 N ρ [ r i ( T ) ] E(T)=\sum_{i=1}^N\rho[r_i(T)] E(T)=i=1∑N​ρ[ri​(T)]

ρ \rho ρ可称为Robust核函数，open3d中封装了如下和函数

核函数封装
L1损失L1Loss ω ( r ) = 1 ∣ r ∣ → ρ ( r ) = ∣ r ∣ \omega(r)=\frac1{\vert r\vert }\to\rho(r)=\vert r\vert ω(r)=∣r∣1​→ρ(r)=∣r∣
L2损失L2Loss ω ( r ) = 1 → ρ ( r ) = r 2 2 \omega(r)=1\to\rho(r)=\frac{r^2}2 ω(r)=1→ρ(r)=2r2​
柯西核CauchyLoss ω ( r ) = 1 1 + ( r k ) 2 → ρ ( r ) = k 2 2 log ⁡ ( 1 + ( r k ) 2 ) \omega(r)=\frac1{1+(\frac r k)^2}\to \rho(r)=\frac{k^2}{2}\log(1+(\frac r k)^2) ω(r)=1+(kr​)21​→ρ(r)=2k2​log(1+(kr​)2)
GM核GMLoss ω ( r ) = k ( k + r 2 ) 2 → ρ ( r ) = r 2 / 2 k + r 2 \omega(r)=\frac{k}{(k+r^2)^2}\to\rho(r)=\frac{r^2/2}{k+r^2} ω(r)=(k+r2)2k​→ρ(r)=k+r2r2/2​
Huber核HuberLoss
Tukey核TukeyLoss

Huber核以及Tukey核相对复杂，表示如下

  • Huber核

ω ( r ) = { 1 ∣ r ∣ ⩽ k k ∣ r ∣ otherwise ⁡ → ρ ( r ) = { r 2 2 ∣ r ∣ < k k ∣ r ∣ − k 2 2 otherwise ⁡ \omega(r)={1|r|⩽\to \rho(r)= ω(r)={1∣r∣k​​∣r∣⩽kotherwise​→ρ(r)={2r2​k∣r∣−2k2​​∣r∣<kotherwise​

  • Tukey核

ω ( r ) = { [ 1 − ( r k ) 2 ] 2 ∣ r ∣ ⩽ k 0 otherwise ⁡ → ρ ( r ) = { k 2 { 1 − [ 1 − ( e k ) 2 ] 3 } 2 ∣ r ∣ < k r 2 2 otherwise ⁡ \omega(r)=\to \rho(r)= ω(r)={[1−(kr​)2]20​∣r∣⩽kotherwise​→ρ(r)=⎩ ⎨ ⎧​2k2{1−[1−(ke​)2]3}​2r2​​∣r∣<kotherwise​

除了L1Loss和L2Loss之外，其他损失函数均有参数 k k k，当 k k k设为0.5时，这四个和函数的图像为

在这里插入图片描述

绘图代码如下

import numpy as np
import matplotlib.pyplot as plt
import open3d as o3d

pipreg = o3d.pipelines.registration

kerrDct = {
"cuchy" : pipreg.CauchyLoss,
"GM"    : pipreg.GMLoss,
"huber" : pipreg.HuberLoss,
"tukey" : pipreg.TukeyLoss
}

fig = plt.figure()
xs = np.linspace(-2,2,1000)
for i,key in enumerate(kerrDct):
    kerr = kerrDct[key](0.5)
    ys = [kerr.weight(x) for x in xs]
    ax = fig.add_subplot(221+i)
    ax.plot(xs, ys)
    plt.title(key)

plt.show()
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23

ICP测试

下面对鲁棒核的效果进行测试，首先打开测试点云，并添加一点噪声

demo = o3d.data.DemoICPPointClouds()
src = o3d.io.read_point_cloud(demo.paths[0])
tar = o3d.io.read_point_cloud(demo.paths[1])

pts = np.array(src.points)

# 添加正态分布的噪声
pts += np.random.normal(0, 0.1, size=pts.shape)
srcNoise = o3d.geometry.PointCloud()
srcNoise.points = o3d.utility.Vector3dVector(pts)

srcDraw = deepcopy(src)
o3d.visualization.draw_geometries([srcDraw.translate((-4.5,0,0)),
    srcNoise])
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14

加完噪声前后的点云图如下，几乎连轮廓都看不出来了

在这里插入图片描述

所以问题就是，右边那一坨五颜六色的东西真的可以和左边的图匹配到一起去吗？如果仍然使用传统的ICP算法，结果如下，可见完全没有配准

在这里插入图片描述

代码为

p2L = pipreg.TransformationEstimationPointToPlane()
regP2L = pipreg.registration_icp(srcNoise, tar, 0.5, trans_init, p2L)

srcP2L = deepcopy(src)
srcP2L.transform(regP2L.transformation)
srcP2L.paint_uniform_color([0, 1, 1])
o3d.visualization.draw_geometries([srcP2L, tar])
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7

接下来，则是见证奇迹的时刻，采用Turkey核来重新配准一下，考虑到核函数的权重会随着距离增大而减小，最后缩减至0，所以阈值在icp函数中显得就不那么重要了，下面随便选一个非常不靠谱的大数10，然后看一下配准结果

loss = o3d.pipelines.registration.TukeyLoss(k=0.1)
turkey = pipreg.TransformationEstimationPointToPlane(loss)
regTurkey = pipreg.registration_icp(srcNoise, tar, 10, trans_init, turkey)

srcTurkey = deepcopy(src)
srcTurkey.transform(regTurkey.transformation)
srcTurkey.paint_uniform_color([0, 1, 1])
o3d.visualization.draw_geometries([srcTurkey, tar])
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8

结果如下，可以说相当靠谱了。

在这里插入图片描述

注：本文转载自blog.csdn.net的微小冷的文章"https://tinycool.blog.csdn.net/article/details/136952562"。版权归原作者所有，此博客不拥有其著作权，亦不承担相应法律责任。如有侵权，请联系我们删除。
复制链接
相关推荐
发表评论

评论记录：

未查询到任何数据！