推荐|python-opencv 边缘检测、直线检测、圆检测

文章目录

Canny算法

除了将目标与背景分离开来，边缘检测也同样是一种图像分割方法，从分割结果来看，adaptiveThreshold函数显然就采取了类似边缘检测的划分方案。

Canny在1986年提出了一种边缘检测算法，因其卓越的性能和准确性而广泛应用于各种图像分析领域。opencv中提供了这种算法，其操作步骤如下

高斯滤波：采用 $5\times5$ 的高斯滤波，对图像进行平滑，以降低灰度波动，使边缘更加明显。
梯度计算：用Sobel核函数对图像滤波，得到两个方向的一阶导数 $G_x, G_y$ ，从而得到图像的梯度 $\sqrt{G_x^2+G_y^2}$ 以及辐角 $\tan^{-1}\frac{G_y}{G_x}$
非极大值抑制：即抑制那些不是局部最大值的梯度值，即一个像素点，只有其梯度幅度大于周围像素点时，才被认为是边缘点。
双阈值处理：通过高阈值 $t_2$ 和低阈值 $t_1$ 来进一步判断边缘，某点若梯度幅度大于 $t_2$ ，则被认为是边缘点；若处于 $t_2$ 和 $t_1$ 之间，则被认为是潜在的边缘点。
边缘跟踪和连接：最后，算法跟踪由边缘像素点组成的线，并连接它们以形成完整的边缘。

令 $t_1=100,t_2=200$ ，则Canny算法的边缘检测结果如下

在这里插入图片描述

实现代码如下。

imgs = {}
imgs['Original'] = ascent().astype(np.uint8)
imgs['edges'] = cv2.Canny(img,100,200)

for i,key in enumerate(imgs, 1):
    plt.subplot(1,2,i)
    plt.imshow(imgs[key],cmap = 'gray')
    plt.title(key)
    plt.axis('off')

plt.show()

【Canny】即为Canny边缘检测函数，其输入参数分别是待检测图像和阈值 $t_1, t_2$ 。

霍夫变换-直线检测

在获取图像边缘后，可能会对边缘的形状产生兴趣。1962年，Hough提出一种直线和圆的识别方案，思路是将图像中的点映射到一个参数空间，这个空间中涵盖了某个几何形状的所有参数，这个变换便被称作霍夫变换（Hough Transform, HT）。

Python中提供了基于HT的直线检测函数，可实现如下效果。

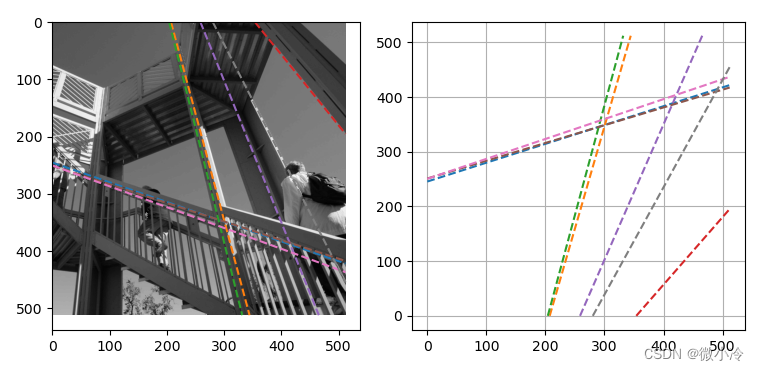
在这里插入图片描述

代码为

img = ascent().astype(np.uint8)
m, n = img.shape

edges = cv2.Canny(img, 50, 150, apertureSize = 3)
lines = cv2.HoughLines(edges,1.1,np.pi/180,200)

【HoughLines】就是HT直线检测函数，其输入的四个参数分别是待检测图像、以像素为单位的距离精度 $p_r$ 、以弧度为单位的角度精度 $p_\theta$ 以及累加平面的阈值参数。 $p_r, p_\theta$ 这两个值设得越大，则会检查出越多的直线。

其检测检测结果由 $(\rho, \theta)$ 来表示，其中 $\rho$ 表示直线与坐标原点 $(0, 0)$ 的距离， $\theta$ 是直线的垂线与 $x$ 轴的夹角。从而直线方程可表示为点法式

$x\cos\theta+y\sin\theta-\rho=0$

对于尺寸为 $m$ 行 $n$ 列的图像来说，四个边框分别是 $x = 0, x = n, y = 0, y = m$ ，记 $c=\cos\theta, s=\sin\theta$ ，则直线与四个边框的交点分别为

$\begin{matrix} (0, \frac{\rho}{s})&(n, \frac{\rho-nc}{s})\\ (\frac{\rho}{c}, 0)&(\frac{\rho-ms}{c}, m)\\ \end{matrix}$

从而绘图代码如下

fig, ax = plt.subplots(1,2)

ax[0].imshow(img, cmap='gray')
for line in lines:
    rho,theta = line[0]
    c = np.cos(theta)
    s = np.sin(theta)
    xs = [0, n, rho/c, (rho-m*s)/c]
    ys = [rho/s, (rho-n*c)/s, 0, m]
    i1, i2 = np.argsort(xs)[1:3]
    ax[0].plot([xs[i1], xs[i2]], [ys[i1], ys[i2]], ls='--')
    ax[1].plot([xs[i1], xs[i2]], [ys[i1], ys[i2]], ls='--')

plt.grid()
plt.show()

霍夫变换-圆形检测

opencv中提供了基于霍夫变换的圆形检测方法，可实现下图所示的检测结果。

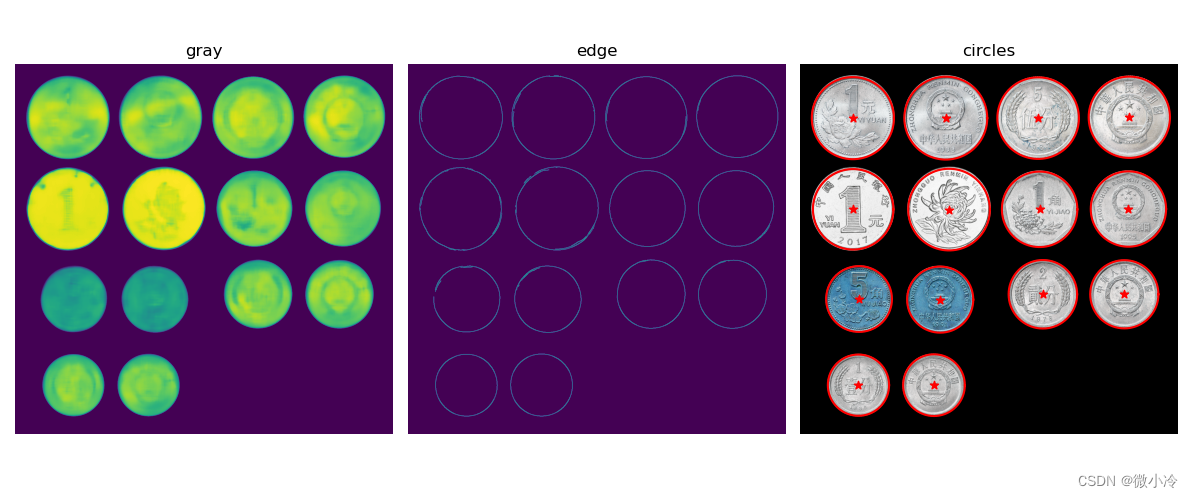
在这里插入图片描述

其实现代码如下。

path = 'coins.png'

coins = {}
img = cv2.imread(path, cv2.IMREAD_COLOR)
gray = cv2.cv2tColor(img, cv2.COLOR_BGR2GRAY)

coins['gray'] = cv2.medianBlur(gray, 25)
coins['edge'] = cv2.Canny(coins['gray'],100,200)

rows = gray.shape[0]
circles = cv2.HoughCircles(coins['gray'], cv2.HOUGH_GRADIENT,
        1, 150, param1=100, param2=30,
        minRadius=1, maxRadius=300)

【HoughCircles】是opencv提供的基于霍夫变换的圆形检测工具。

函数参数说明：

image: 待检测灰度图像。
method: 检测圆的方法。
dp: 霍夫变换的分辨率，值越大，检测的圆越少，但越准确。
minDist: 圆心之间的最小距离。
param1: 边缘检测时使用Canny算子的高阈值，低阈值是高阈值的一半。
param2: 用于圆心检测的参数。
minRadius, maxRadius: 圆半径的最小值和最大值。

其中，opencv通提供了四种检测圆的方法，其method参数可选值如下

【cv2.HOUGH_GRADIENT】霍夫梯度法，通过计算图像中的梯度来确定圆心的可能位置，然后对这些位置进行投票，以确定真实的圆心。这种方法的问题是对噪声敏感。
【cv2.HOUGH_GRADIENT_ALT】霍夫梯度法的另一种实现。
【cv2.HOUGH_PROBABILISTIC】概率霍夫变换，与霍夫梯度法的区别是，并不通过全局投票来确定圆心，而检查一些候选点是否符合圆的方程，它通常会产生较少的假阳性结果，但可能检测不到某些圆。
【cv2.HOUGH_MULTI_SCALE】多尺度霍夫变换，将在不同尺度上应用霍夫变换，对缩放、旋转和倾斜变化具有更好的鲁棒性。和其他方法相比，该方法可能会检测到更多的圆，但也更吃计算资源。

绘图代码如下。

coins['circles'] = img
for i,key in enumerate(coins,1):
    ax = plt.subplot(1,3,i)
    plt.title(key)
    plt.imshow(coins[key])
    plt.axis('off')

th = np.deg2rad(np.arange(361))
for x,y,r in circles[0]:
    xs = x + r*np.cos(th)
    ys = y + r*np.sin(th)
    plt.scatter(x, y, marker='*', color='red')
    plt.plot(xs, ys, color='red')

plt.show()

文章目录

Canny算法

霍夫变换-直线检测

霍夫变换-圆形检测

评论记录：