python图像处理教程：初步

图像变换

尽管numpy提供了一些矩阵函数，但图像处理是一个十分浩瀚的领域，numpy的体量显然有些不够。相比之下，【scipy】封装了【ndimage】模块，即专用的多维数组处理模块，自然也涵盖了二维图像的处理。

ndimage中提供了对数组进行平移、缩放以及旋转操作的函数，分别是shift, zoom, rotate，可以实现下面的变换效果

import numpy as np
import matplotlib.pyplot as plt
from scipy.ndimage import *
from scipy.misc import face
img = face()

imDct = {
    "original": img,
    "shift" : shift(img, [50, 50, 0]),
    "zoom" : zoom(img, [1.5, 2, 1]),
    "rotate" : rotate(img, 15, axes=(1,0))
}

fig = plt.figure()
for i, key in enumerate(imDct):
    fig.add_subplot(2,2,i+1)
    plt.imshow(imDct[key])
    plt.title(key)
    plt.axis('off')

plt.show()

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20
• 21

除了输入图像外，平移和缩放均有一个参数，表示图像数据的三个坐标轴宽、高、通道的平移与缩放情况；旋转有两个参数，分别表示旋转角度和旋转轴。

这些变换都是通过插值来实现的，通过参数order可以指定几何变换的插值次数，参数prefilter若设为为True，则会在插值前进行样条滤波。

从上图可知，当平移和旋转在对原数组进行操作后，空出来的区域会被填补为黑色，这由两个参数决定，参数mode用于指定填充方法，默认为constant模式，在此模式下，会用某个常数来填充空余区域，这个数值由参数cval指定。

填充模式

设数组中的值为a b c d，当mode参数取不同的模式时，其填充方法如下

• reflect/grid-mirror 反射取点【d c b a | a b c d | d c b a】
• mirror 反射取点，不包括边缘点 【d c b | a b c d | c b a】
• constant/grid-constant 添加常数k【k k k k | a b c d | k k k k】
• grid-constant 【k k k k | a b c d | k k k k】
• nearest 就近取点 【a a a a | a b c d | d d d d】
• grid-wrap 循环处理 【a b c d | a b c d | a b c d】
• wrap 循环处理，不包括边缘点【d b c d | a b c d | b c a b】

下面以旋转为例，进一步对比不同mode下的变换效果，旋转函数中有一个axes参数，表示旋转所在的坐标平面。

imDct = {
    "mirror" : rotate(img, 15, axes=(1,0), mode='mirror'),
    "reflect" : rotate(img, 30, axes=(1,0), mode='reflect'),
    "nearest" : rotate(img, 45, axes=(1,0), mode='nearest'),
}
fig = plt.figure()
for i, key in enumerate(imDct):
    fig.add_subplot(1,3,i+1)
    plt.imshow(imDct[key])
    plt.title(key)
    plt.axis('off')


plt.show()

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14

效果如下

图像插值

由于数组本身是格点化了的，所以对数组的旋转、平移和缩放，并不像实数空间中那么简单。以一维的平移为例，现有三个点，坐标为$0,1,2$，值对应为$a,b,c$，现在将这个数轴向右平移$0.5$，则这$a,b,c$三个点的坐标就变成了$0.5,1.5,2.5$，但数组中不允许出现非整数的坐标，所以显示的仍然是$0,1,2$位置处的值，所以就需要通过$0.5,1.5,2.5$位置处的值，来插值得到$0,1,2$位置处的值。

几何变换中所用到的插值方法，就是样条插值，而样条插值的核心步骤，是根据临近点做数据拟合，拟合时最重要的参数就是阶数，这也是旋转、缩放等操作中order参数的源头。

在【ndimage】中，提供了一维样条插值和多维样条插值函数，分别是spline_filter1d和spline_filter，这两个函数的参数也包括order和mode。而一维插值函数还有一个坐标轴选项，用以约定插值的方向，其差别如下。

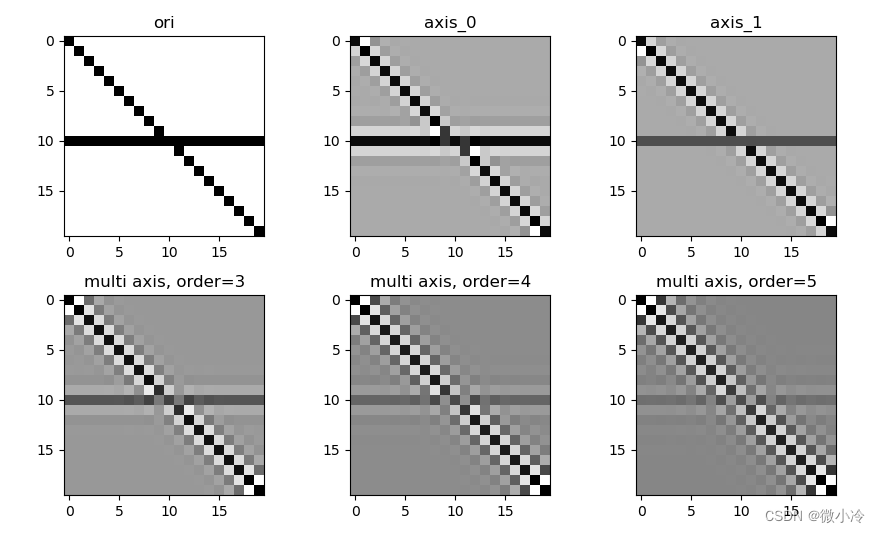
绘图代码为

import numpy as np
import matplotlib.pyplot as plt
from scipy.ndimage import *
ori = np.eye(20)
ori[10, :] = 1.0

fDct = {
    "ori" : ori,
    "axis_0" : spline_filter1d(ori, axis=0),
    "axis_1" : spline_filter1d(ori, axis=1),
    "multi axis, order=3" : spline_filter(ori, order=3),
    "multi axis, order=4" : spline_filter(ori, order=4),
    "multi axis, order=5" : spline_filter(ori, order=5)
}

fig = plt.figure()
for i, key in enumerate(fDct):
    fig.add_subplot(2, 3, i+1)
    plt.imshow(fDct[key], cmap='gray_r')
    plt.title(key)

plt.show()

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20
• 21
• 22