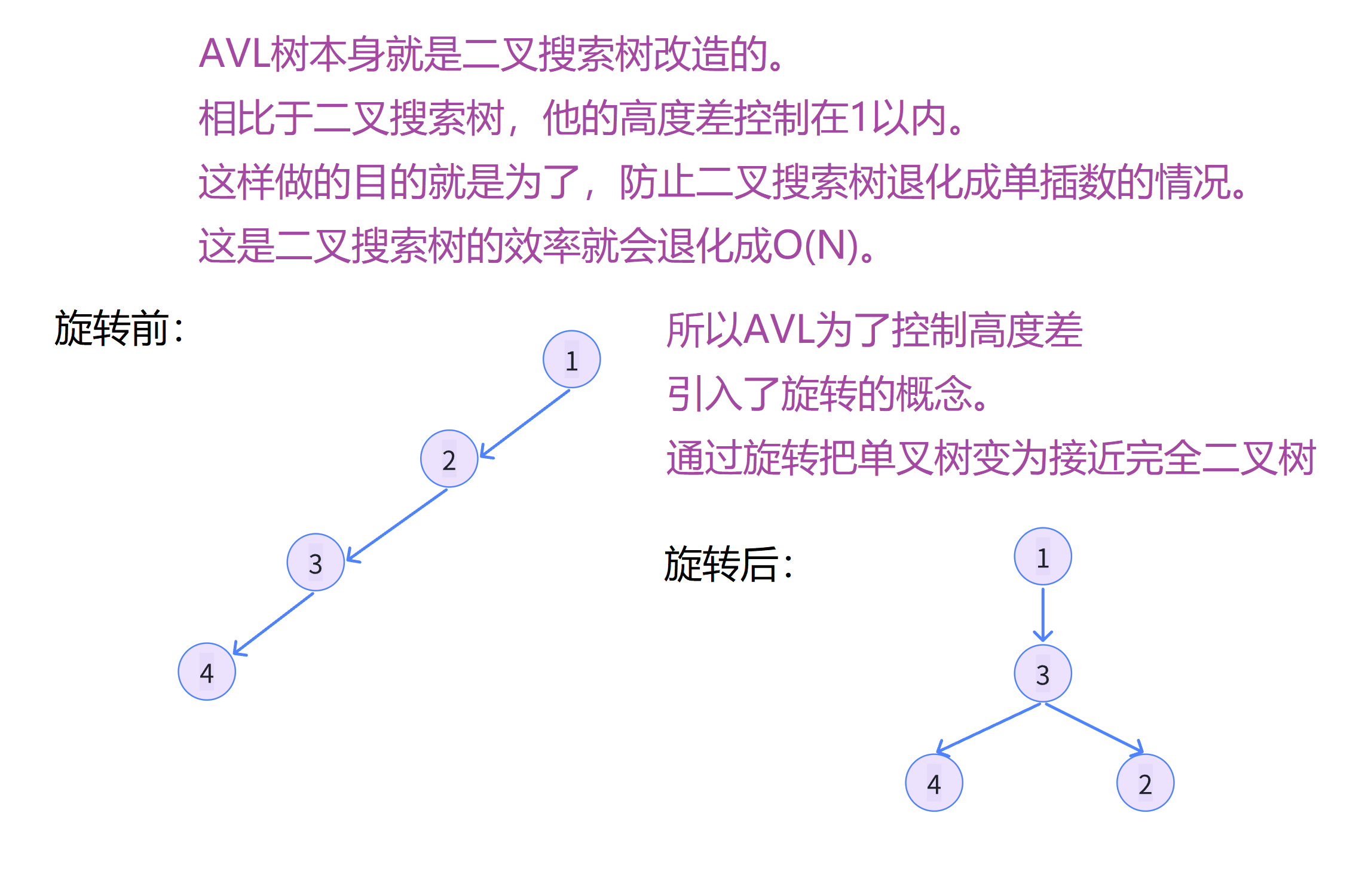
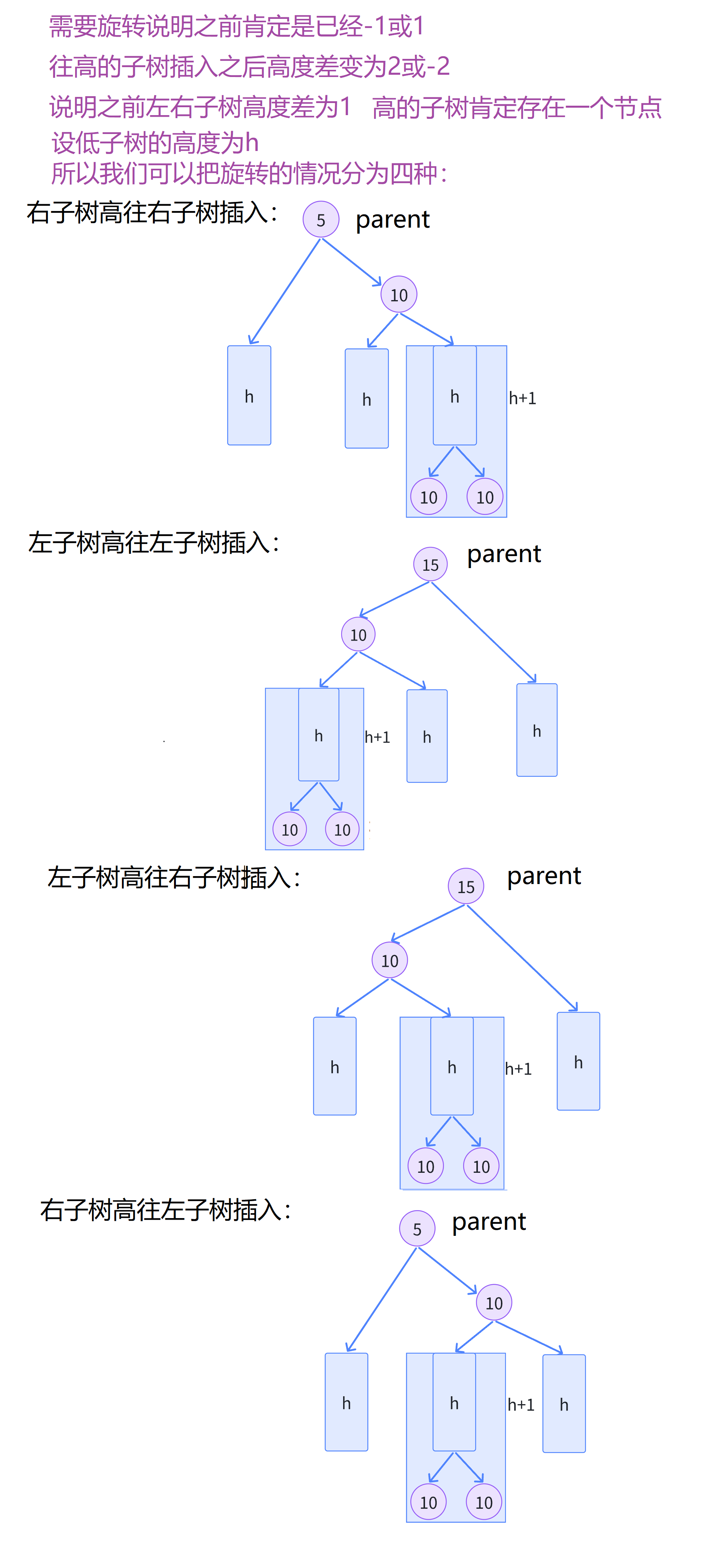
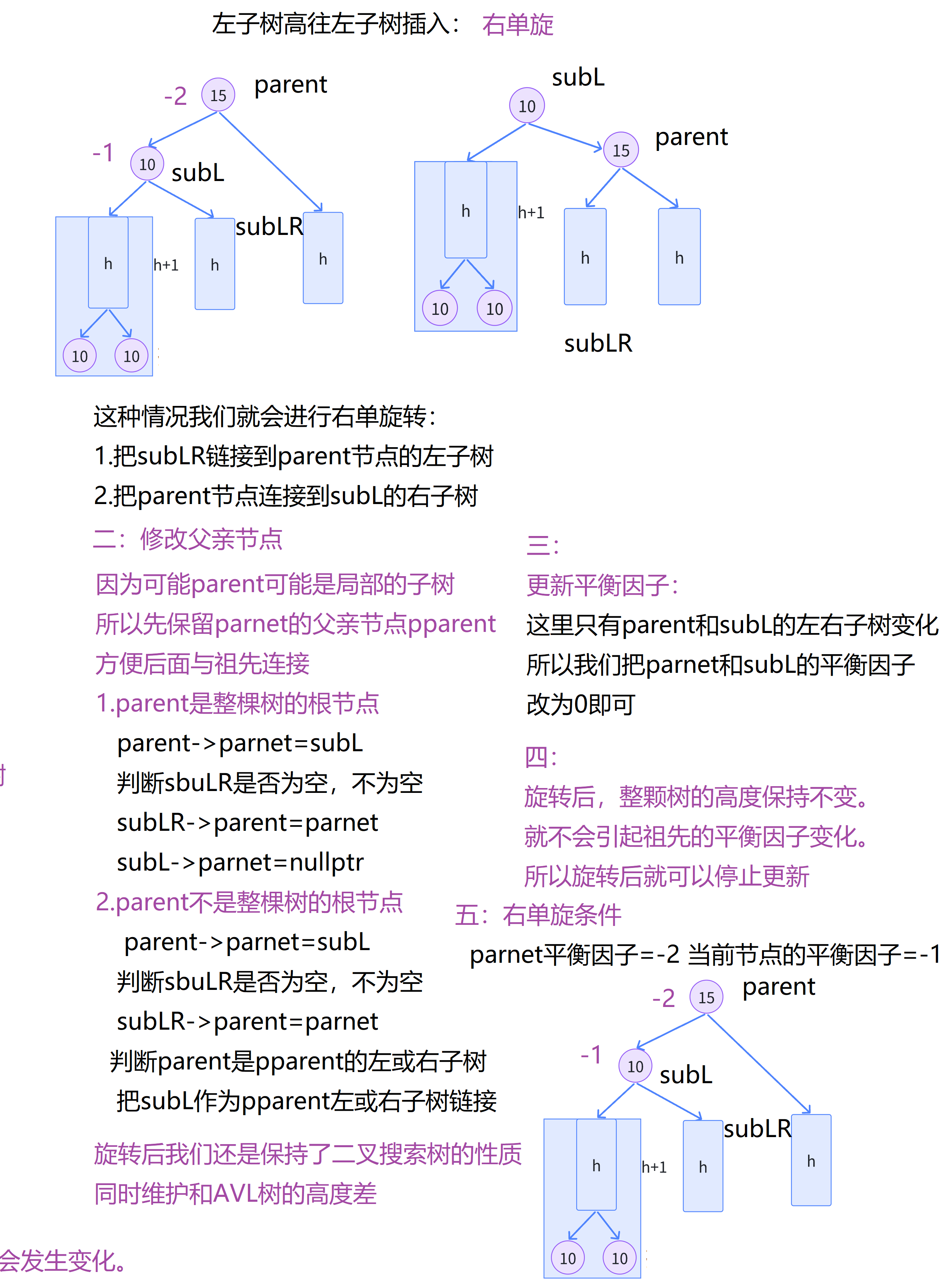
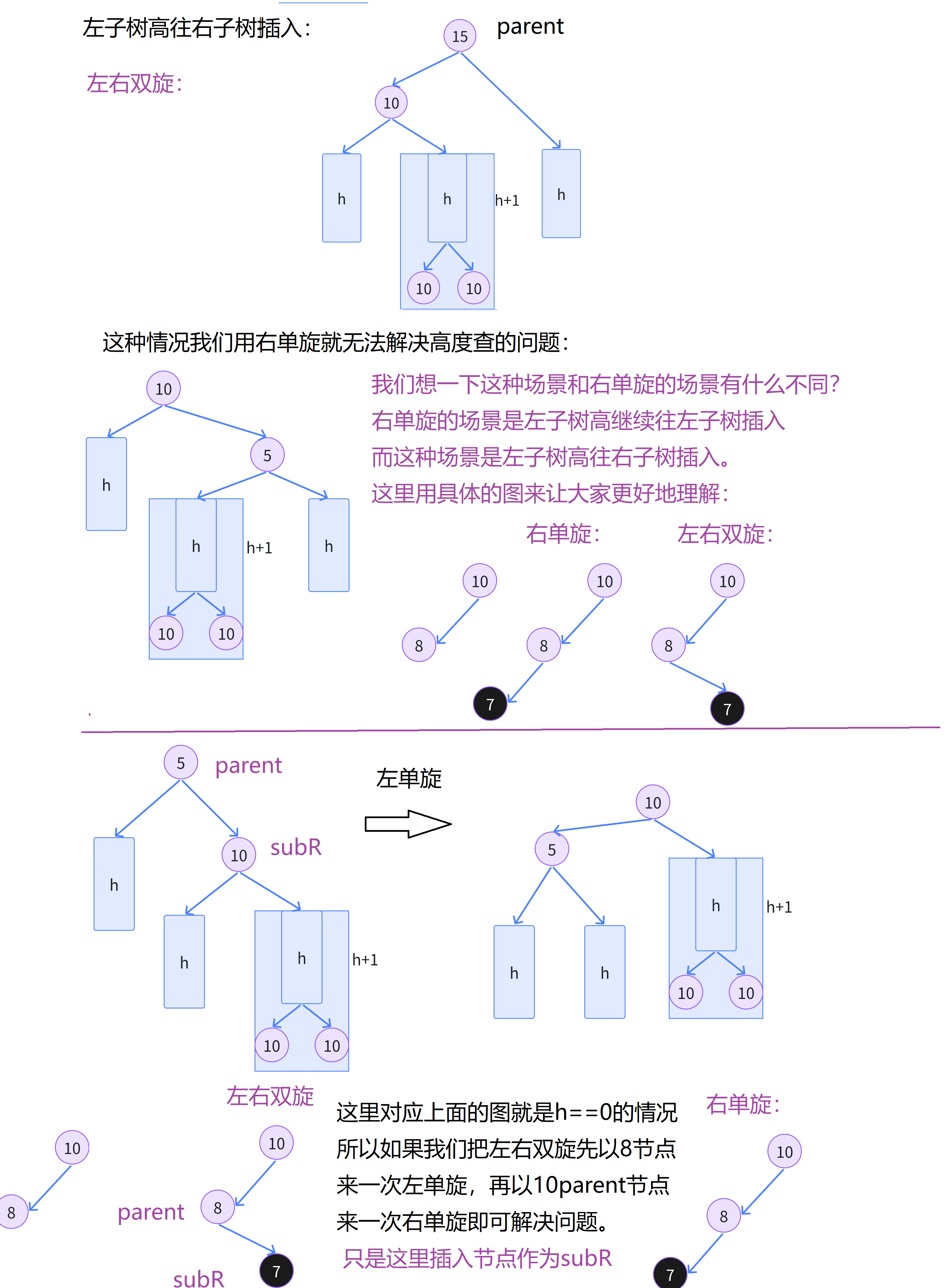
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 左单旋和右单旋类似。
void RoRateL ( node* parent)
{
node* subR = parent-> right;
node* subRL = subR-> left;
node* pparnet = parent-> parent;
parent-> right = subRL;
if ( subRL)
{
subRL-> parent = parent;
}
subR-> left = parent;
parent-> parent = subR;
if ( pparnet== nullptr )
{
_root = subR;
subR-> parent = nullptr ;
}
else
{
if ( pparnet-> left == parent)
{
pparnet-> left = subR;
}
else
{
pparnet-> right = subR;
}
subR-> parent = pparnet;
}
subR-> bf = parent-> bf = 0 ;
}
class="hljs-button signin active" data-title="登录复制" data-report-click="{"spm":"1001.2101.3001.4334"}"> class="hide-preCode-box">1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 左右双旋的就是先左单旋再右单旋。
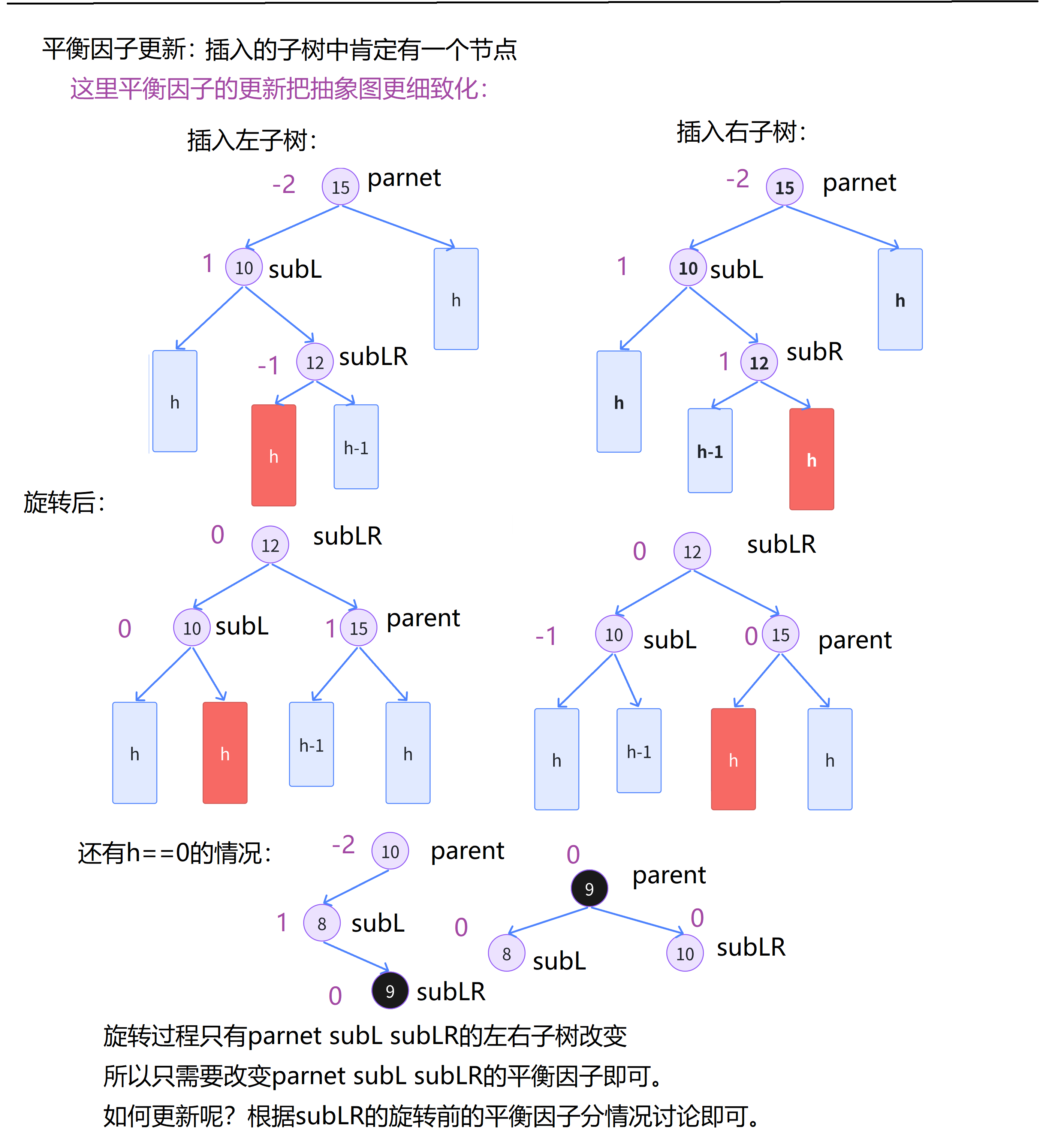
void RoRateLR ( node* parent)
{
node* subL = parent-> left;
node* subLR = subL-> right;
int bf = subLR-> bf;
RoRateL ( subL) ;
RoRateR ( parent) ;
if ( bf == 0 )
{
parent-> bf = 0 ;
subL-> bf = 0 ;
subLR-> bf = 0 ;
}
else if ( bf == 1 )
{
parent-> bf = 0 ;
subL-> bf = - 1 ;
subLR-> bf = 0 ;
}
else if ( bf == - 1 )
{
parent-> bf = 1 ;
subL-> bf = 0 ;
subLR-> bf = 0 ;
}
else
{
assert ( false ) ;
}
}
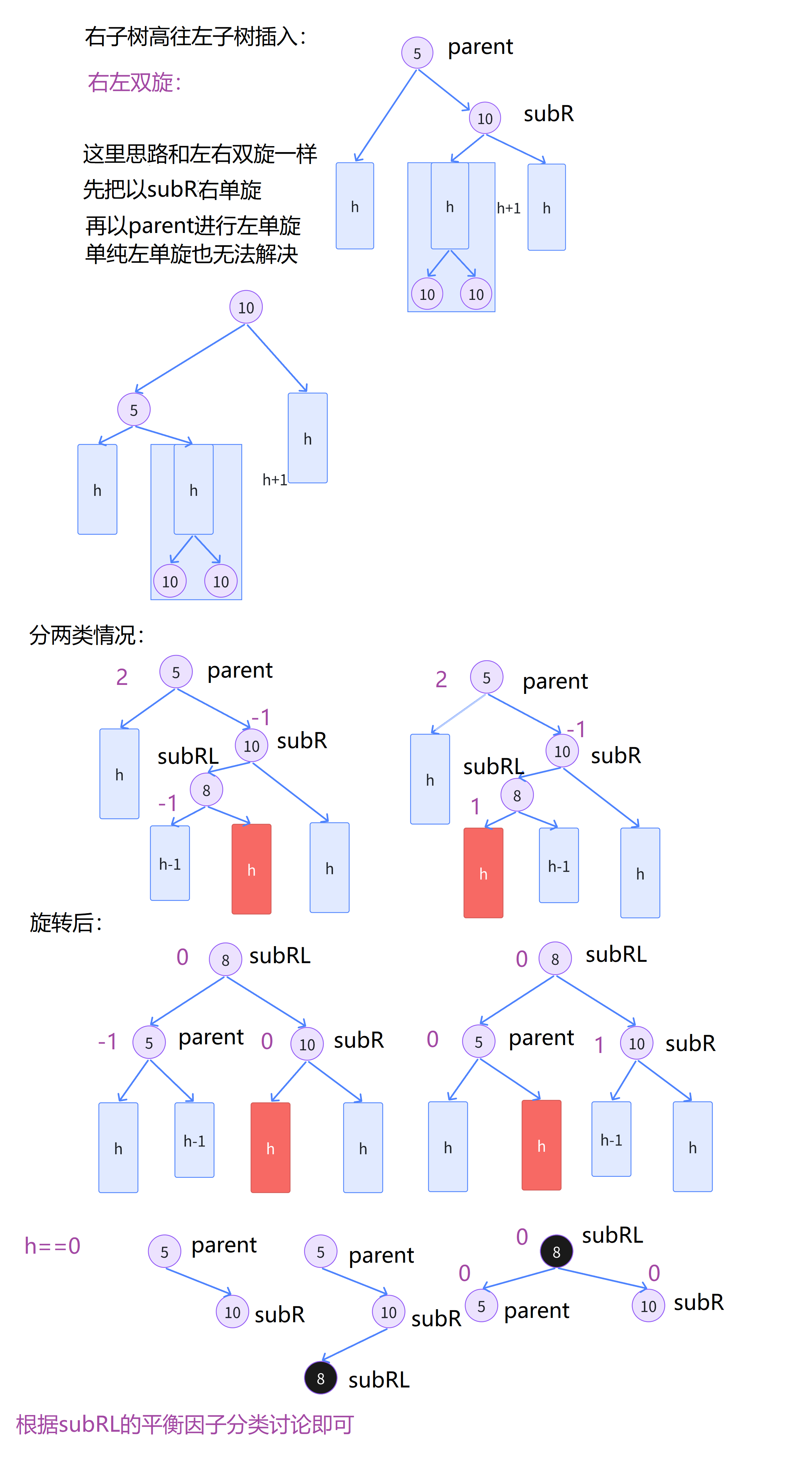
class="hljs-button signin active" data-title="登录复制" data-report-click="{"spm":"1001.2101.3001.4334"}">1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 右左双旋情况和左右双旋类似,这里就不过多赘述了。
结合前面的知识我们就可以写出二叉搜索树的插入了。
void RoRateR ( node* parent)
{
node* subL = parent-> left;
node* subLR = subL-> right;
node* pparnet = parent-> parent;
parent-> left = subLR;
if ( subLR)
{
subLR-> parent = parent;
}
subL-> right = parent;
parent-> parent = subL;
if ( pparnet == nullptr )
{
_root = subL;
subL-> parent = nullptr ;
}
else
{
if ( pparnet-> left == parent)
{
pparnet-> left = subL;
}
else
{
pparnet-> right = subL;
}
subL-> parent = pparnet;
}
subL-> bf = parent-> bf = 0 ;
}
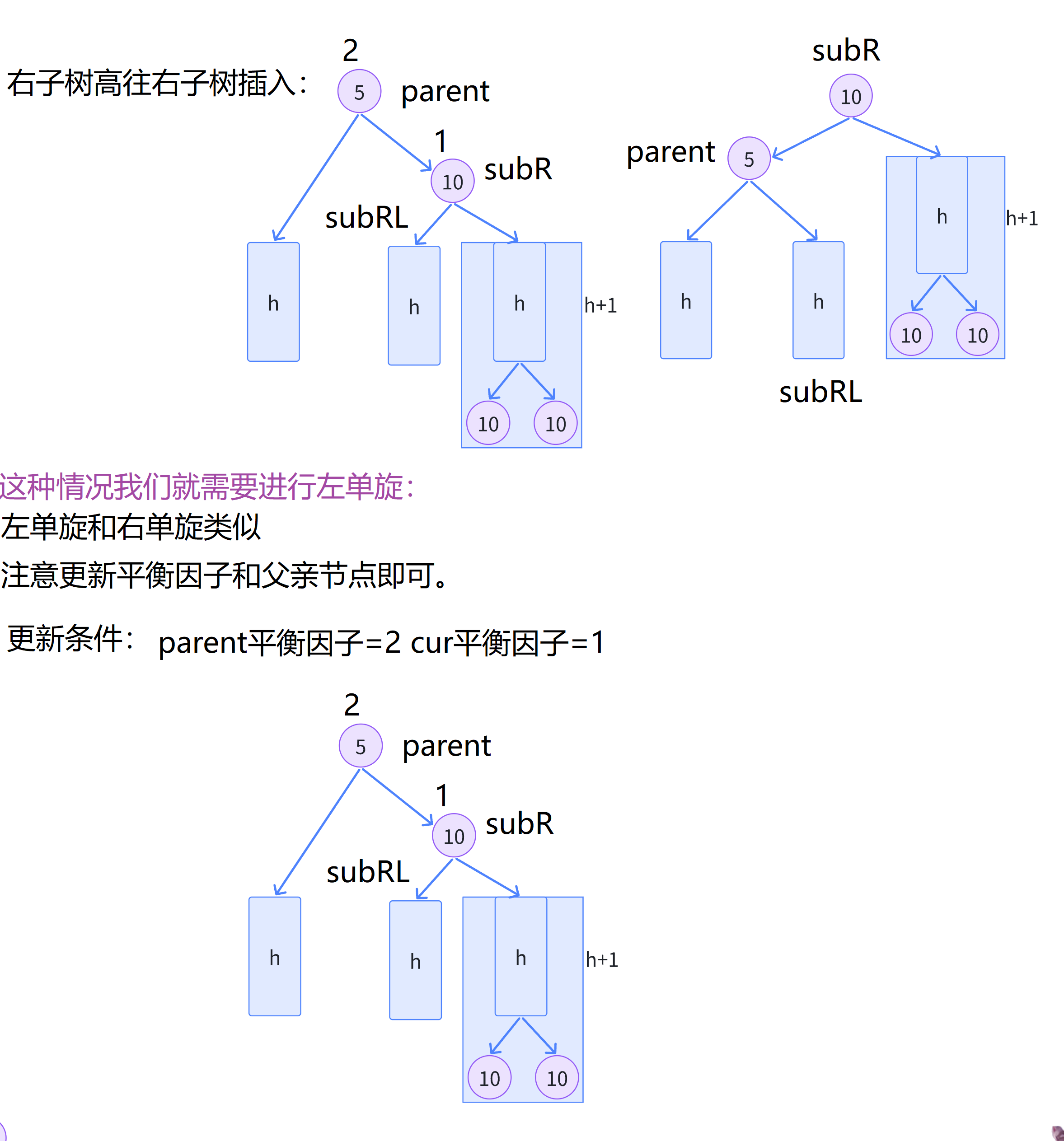
void RoRateL ( node* parent)
{
node* subR = parent-> right;
node* subRL = subR-> left;
node* pparnet = parent-> parent;
parent-> right = subRL;
if ( subRL)
{
subRL-> parent = parent;
}
subR-> left = parent;
parent-> parent = subR;
if ( pparnet== nullptr )
{
_root = subR;
subR-> parent = nullptr ;
}
else
{
if ( pparnet-> left == parent)
{
pparnet-> left = subR;
}
else
{
pparnet-> right = subR;
}
subR-> parent = pparnet;
}
subR-> bf = parent-> bf = 0 ;
}
void RoRateLR ( node* parent)
{
node* subL = parent-> left;
node* subLR = subL-> right;
int bf = subLR-> bf;
RoRateL ( subL) ;
RoRateR ( parent) ;
if ( bf == 0 )
{
parent-> bf = 0 ;
subL-> bf = 0 ;
subLR-> bf = 0 ;
}
else if ( bf == 1 )
{
parent-> bf = 0 ;
subL-> bf = - 1 ;
subLR-> bf = 0 ;
}
else if ( bf == - 1 )
{
parent-> bf = 1 ;
subL-> bf = 0 ;
subLR-> bf = 0 ;
}
else
{
assert ( false ) ;
}
}
void RoRateRL ( node* parent)
{
node* subR = parent-> right;
node* subRL = subR-> left;
int bf = subRL-> bf;
RoRateR ( subR) ;
RoRateL ( parent) ;
if ( bf == 0 )
{
parent-> bf = 0 ;
subR-> bf = 0 ;
subRL-> bf = 0 ;
}
else if ( bf == 1 )
{
parent-> bf = - 1 ;
subR-> bf = 0 ;
subRL-> bf = 0 ;
}
else if ( bf == - 1 )
{
parent-> bf = 0 ;
subR-> bf = 1 ;
subRL-> bf = 0 ;
}
else
{
assert ( false ) ;
}
}
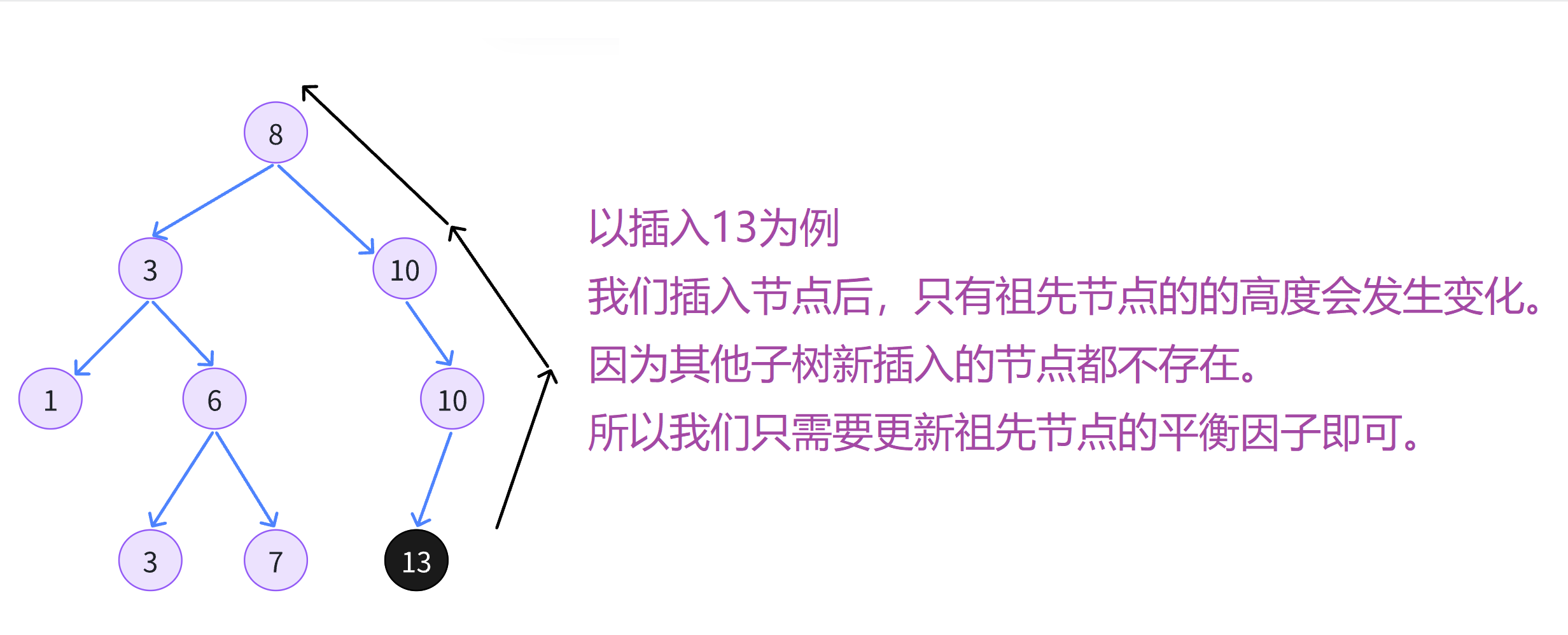
bool Insert ( const k& x, const v& v)
{
if ( _root == nullptr )
{
_root = new node ( x, v) ;
return true ;
}
node* cur = _root;
node* parent = nullptr ;
while ( cur)
{
if ( x < cur-> _key)
{
parent = cur;
cur = cur-> left;
}
else if ( x > cur-> _key)
{
parent = cur;
cur = cur-> right;
}
else
{
return false ;
}
}
cur = new node ( x, v) ;
if ( x > parent-> _key)
{
parent-> right = cur;
}
else
{
parent-> left = cur;
}
cur-> parent = parent;
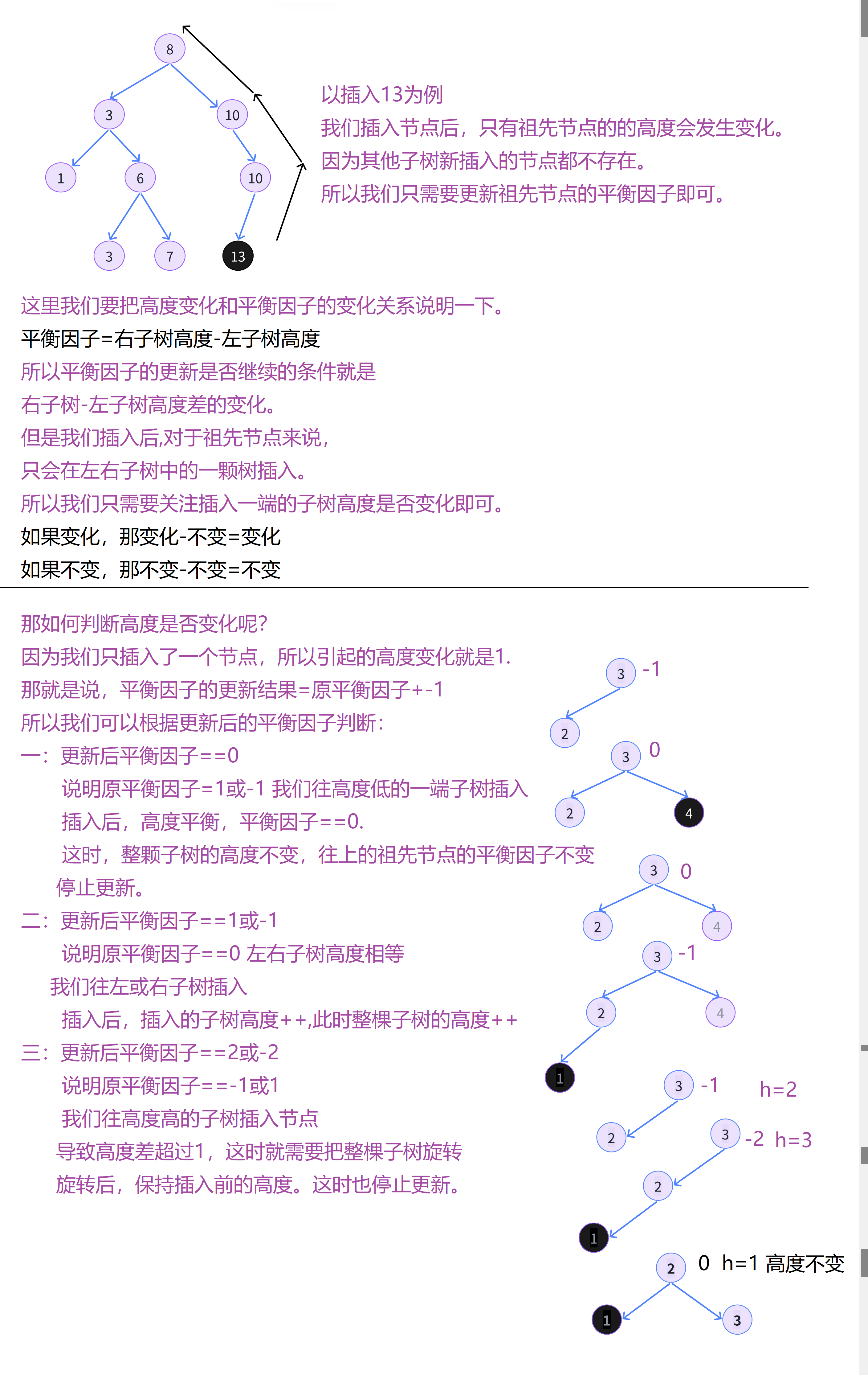
while ( parent)
{
if ( cur == parent-> left)
parent-> bf-- ;
else
parent-> bf++ ;
if ( parent-> bf == 0 )
{
break ;
}
else if ( parent-> bf == 1 || parent-> bf == - 1 )
{
cur = parent;
parent = parent-> parent;
}
else if ( parent-> bf == 2 || parent-> bf == - 2 )
{
if ( parent-> bf == - 2 && cur-> bf == - 1 )
{
RoRateR ( parent) ;
}
else if ( parent-> bf == 2 && cur-> bf == 1 )
{
RoRateL ( parent) ;
}
else if ( parent-> bf == - 2 && cur-> bf == 1 )
{
RoRateLR ( parent) ;
}
else if ( parent-> bf == 2 && cur-> bf == - 1 )
{
RoRateRL ( parent) ;
}
else
{
assert ( false ) ;
}
break ;
}
else
{
assert ( false ) ;
}
}
return true ;
}
class="hljs-button signin active" data-title="登录复制" data-report-click="{"spm":"1001.2101.3001.4334"}">1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 在避免了二叉搜索树退化为单叉树的情况。
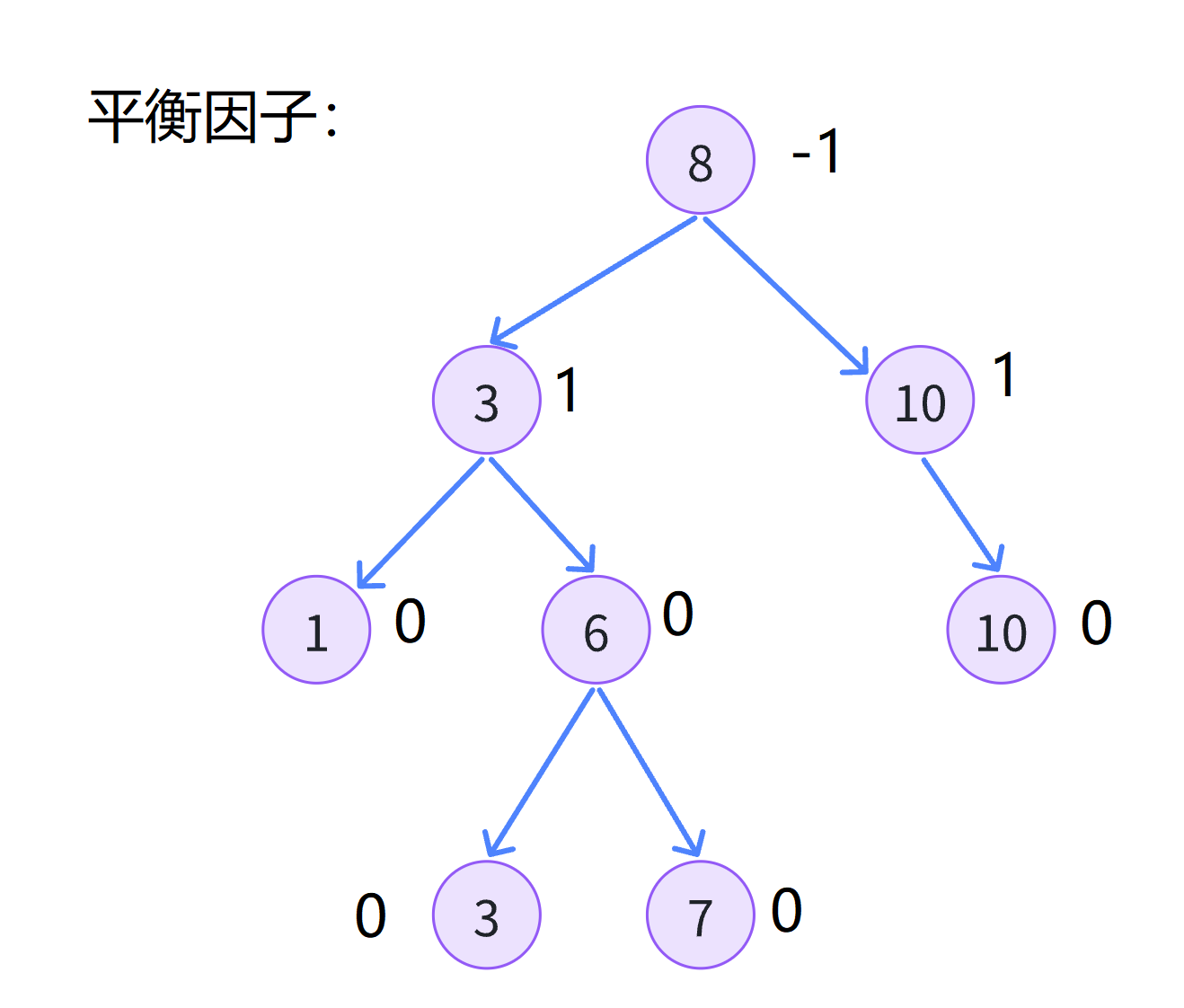
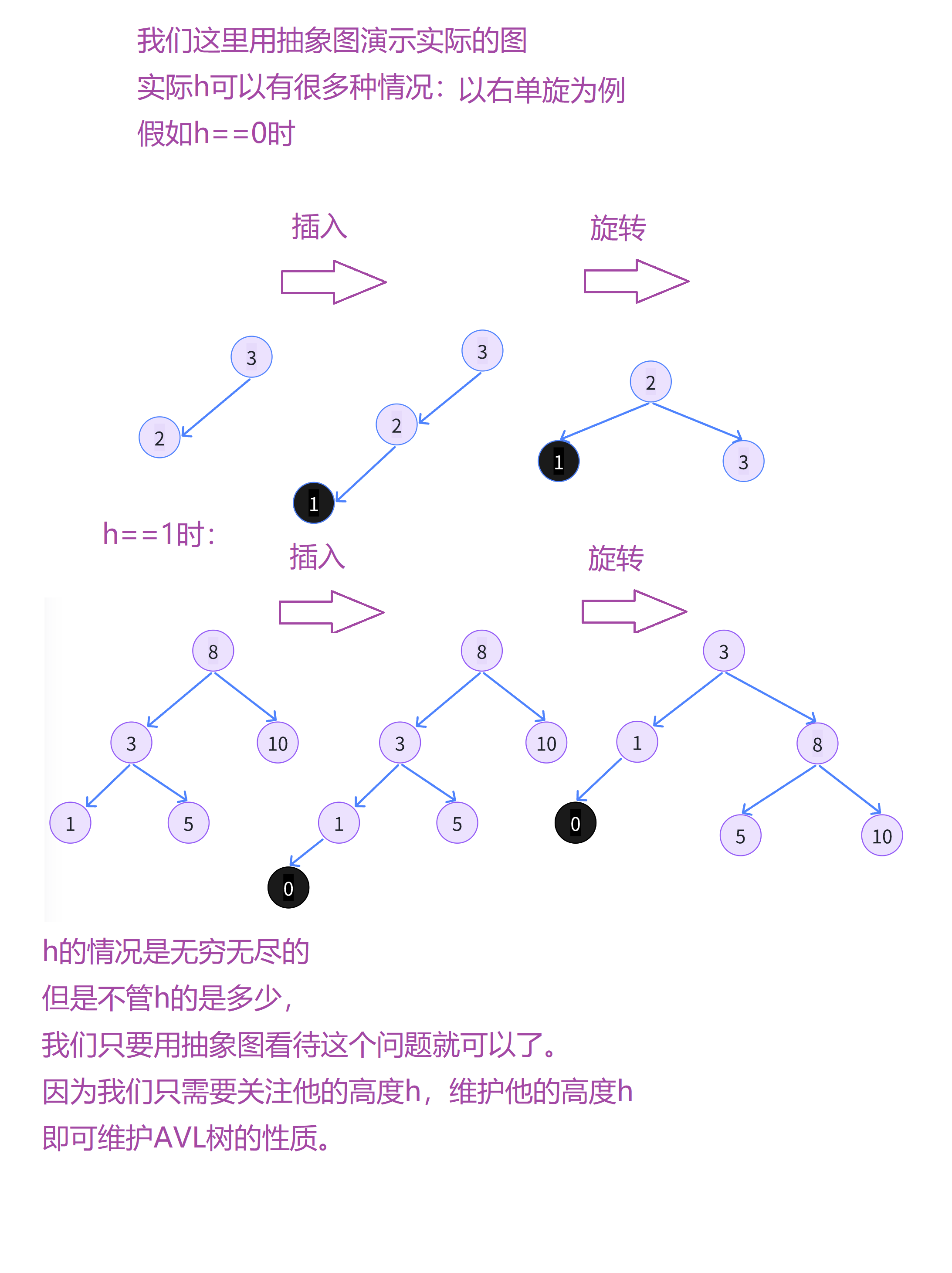
AVL树我们可以递归 检测每颗子树的左右高度差是否不差过1即可。
void Inorder ( )
{
_Inorder ( _root) ;
cout << endl;
}
bool IsBalanceTree ( )
{
return _IsBalanceTree ( _root) ;
}
bool _IsBalanceTree ( const node* root)
{
if ( nullptr == root)
return true ;
int leftHeight = _Height ( root-> left) ;
int rightHeight = _Height ( root-> right) ;
int diff = rightHeight - leftHeight;
if ( abs ( diff) >= 2 )
{
cout << root-> _value << "高度差异常" << endl;
return false ;
}
if ( root-> bf != diff)
{
cout << root-> _key << "平衡因子异常" << endl;
return false ;
}
return _IsBalanceTree ( root-> left) && _IsBalanceTree ( root-> right) ;
}
void _Inorder ( const node* root)
{
if ( root == nullptr )
{
return ;
}
_Inorder ( root-> left) ;
cout << root-> _key << ":" << root-> _value<< endl;
_Inorder ( root-> right) ;
}
size_t Size ( )
{
return _Size ( _root) ;
}
size_t _Size ( const node* parent)
{
if ( parent)
{
return 1 + _Size ( parent-> left) + _Size ( parent-> right) ;
}
else
{
return 0 ;
}
}
size_t Height ( )
{
return _Height ( _root) ;
}
size_t _Height ( const node* parent)
{
if ( parent)
{
return 1 + max ( _Height ( parent-> left) , _Height ( parent-> right) ) ;
}
else
{
return 0 ;
}
}
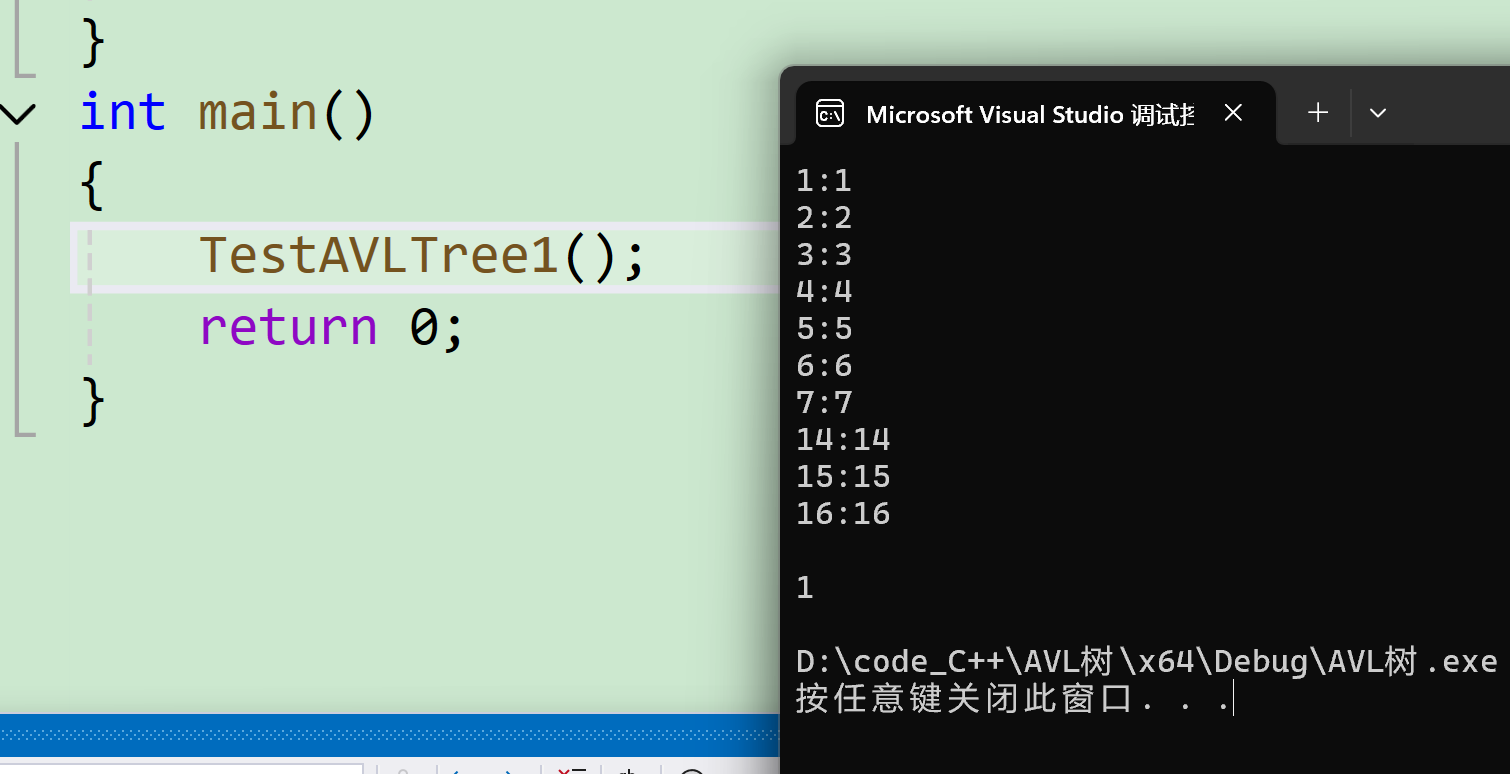
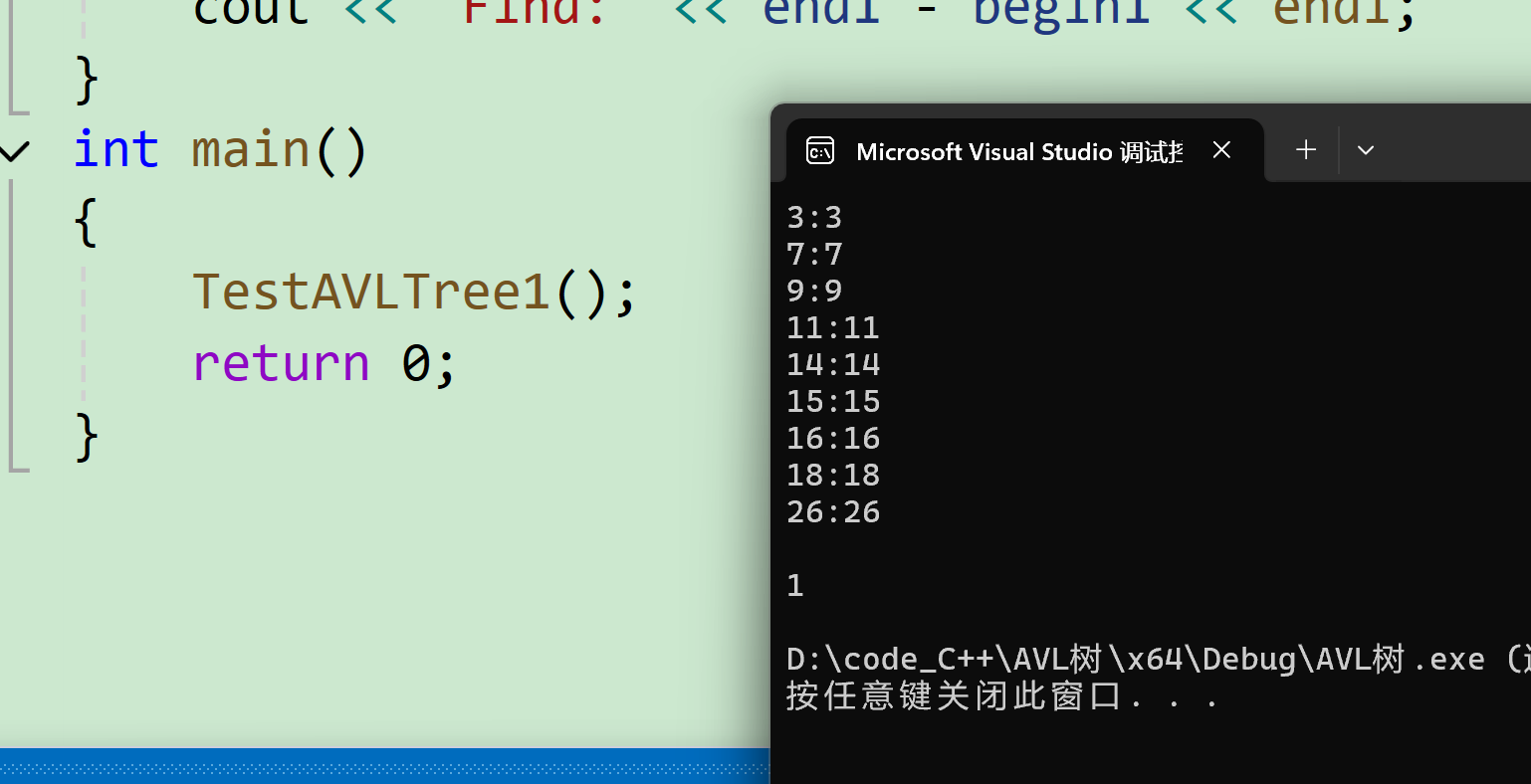
class="hljs-button signin active" data-title="登录复制" data-report-click="{"spm":"1001.2101.3001.4334"}">1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 void TestAVLTree1 ( )
{
AVL:: AVLTree< int , int > t;
int a[ ] = { 4 , 2 , 6 , 1 , 3 , 5 , 15 , 7 , 16 , 14 } ;
for ( auto e : a)
{
t. Insert ( e, e) ;
}
t. Inorder ( ) ;
cout << t. IsBalanceTree ( ) << endl;
}
class="hljs-button signin active" data-title="登录复制" data-report-click="{"spm":"1001.2101.3001.4334"}">
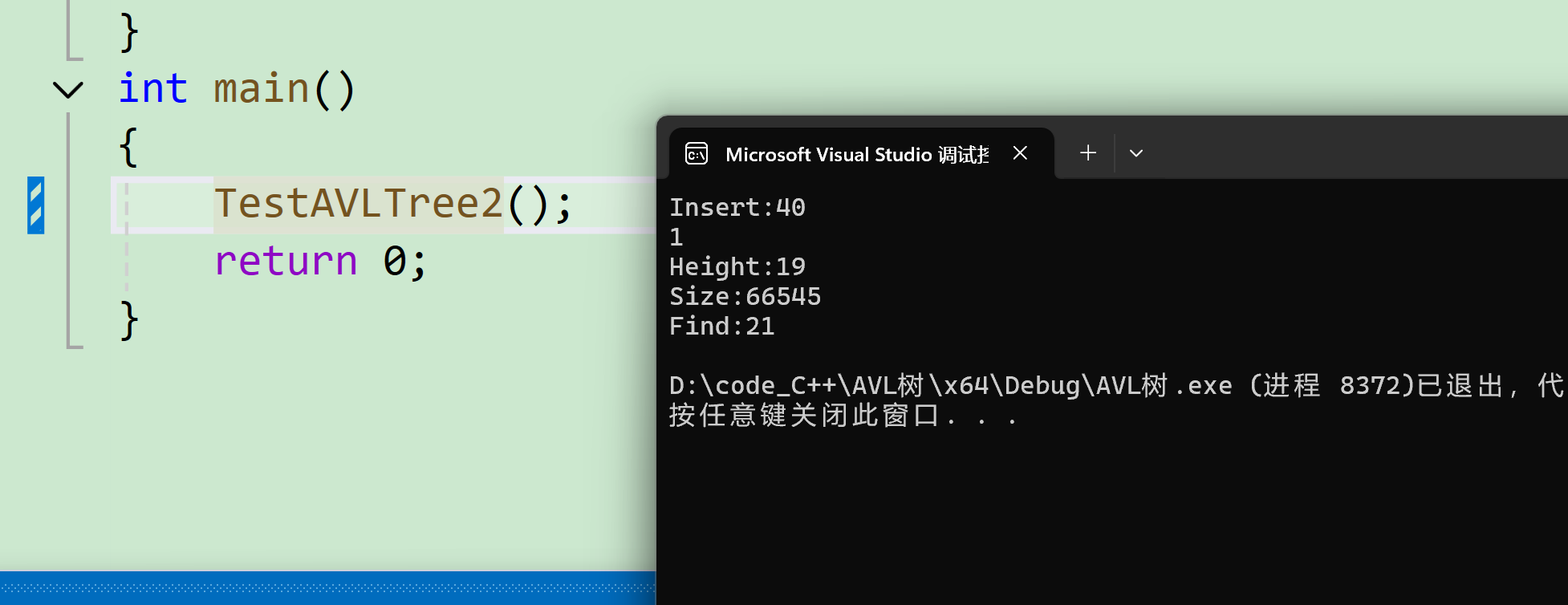
void TestAVLTree2 ( )
{
const int N = 100000 ;
vector< int > v;
v. reserve ( N) ;
srand ( time ( 0 ) ) ;
for ( size_t i = 0 ; i < N; i++ )
{
v. push_back ( rand ( ) + i) ;
}
size_t begin2 = clock ( ) ;
AVL:: AVLTree< int , int > t;
for ( auto e : v)
{
t. Insert ( e, e) ;
}
size_t end2 = clock ( ) ;
cout << "Insert:" << end2 - begin2 << endl;
cout << t. IsBalanceTree ( ) << endl;
cout << "Height:" << t. Height ( ) << endl;
cout << "Size:" << t. Size ( ) << endl;
size_t begin1 = clock ( ) ;
for ( size_t i = 0 ; i < N; i++ )
{
t. Find ( ( rand ( ) + i) ) ;
}
size_t end1 = clock ( ) ;
cout << "Find:" << end1 - begin1 << endl;
}
class="hljs-button signin active" data-title="登录复制" data-report-click="{"spm":"1001.2101.3001.4334"}">1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36
这就是AVL树的深度剖析。大家自己好好消化!今天就分享到这!感谢各位的耐心垂阅!咱们下期见!拜拜~
data-report-view="{"mod":"1585297308_001","spm":"1001.2101.3001.6548","dest":"https://blog.csdn.net/2301_81670477/article/details/144308070","extend1":"pc","ab":"new"}">>
大白的编程日记
class="blog_extension_card_cont_r">
微信名片






 class="blog_extension_card_cont">
class="blog_extension_card_cont">


评论记录:
回复评论: