介绍

AlexNet 是一种深度卷积神经网络（CNN），由 Alex Krizhevsky、Ilya Sutskever 和 Geoffrey E. Hinton 在 2012 年提出，并在当年的 ImageNet 大规模视觉识别挑战赛（ILSVRC）中取得了第一名的成绩。这一成就标志着深度学习在计算机视觉领域的重大突破，极大地推动了该领域的发展。

架构特点

• 输入尺寸：AlexNet 接受 224x224x3（宽 x 高 x RGB 通道数）大小的图像作为输入。
• 卷积层：
  • AlexNet 包含 5 个卷积层，其中前三个卷积层后面接有最大池化层和局部响应归一化层（LRN）。后两个卷积层则直接连接到全连接层。
  • 第一层使用较大的卷积核（11x11），步长为 4，以捕捉大范围的空间信息；后续几层逐渐减小卷积核大小（5x5 和 3x3），以便提取更细粒度的特征。
  • 每个卷积层都应用了 ReLU 激活函数，这有助于加速训练过程并缓解梯度消失问题。
• 池化层：
  • 最大池化层用于降低特征图的空间维度，减少参数数量并控制过拟合。
• 局部响应归一化（LRN）：
  • LRN 对局部神经元活动进行归一化处理，增强了模型的泛化能力。
• 全连接层：
  • AlexNet 有两个大的全连接层，每个包含 4096 个神经元。这些层负责整合前面所有层提取出的特征，并映射到最终的输出类别。
  • 全连接层之后通常会有一个 Dropout 层，用来随机丢弃一部分神经元，防止过拟合。
• 输出层：
  • 输出层通过 Softmax 函数将预测值转换为概率分布，对应于 ImageNet 数据集中的 1000 类别标签。

创新点与贡献

• GPU 加速：AlexNet 是最早利用 GPU 来加速训练过程的网络之一，显著缩短了训练时间。
• ReLU 激活函数：引入 ReLU 代替传统的 Sigmoid 或 Tanh 激活函数，加快了训练速度并提高了性能。
• Dropout 技术：通过在网络中添加 Dropout 层来减少过拟合现象，提升了模型的泛化能力。
• 数据增强：为了增加训练样本的多样性，AlexNet 使用了镜像翻转和裁剪等方法对原始图像进行了扩充。

影响与意义

AlexNet 的成功不仅在于它在 ILSVRC 上取得的优异成绩，更重要的是它证明了深度卷积神经网络在大规模图像分类任务上的巨大潜力。自那时以来，许多新的 CNN 架构如 VGGNet、GoogLeNet、ResNet 等相继出现，它们在不同方面改进和发展了 AlexNet 的思想和技术，共同推动了深度学习和计算机视觉领域的快速发展。

总之，AlexNet 作为一个里程碑式的模型，开启了现代深度学习研究的新纪元，其设计理念和技术创新至今仍然影响着众多研究工作。

ISLVRC 2012

• 训练集：1,281,167张已标注图片
• 验证集：50,000张已标注图片
• 测试集：100,000张未标注图片
  

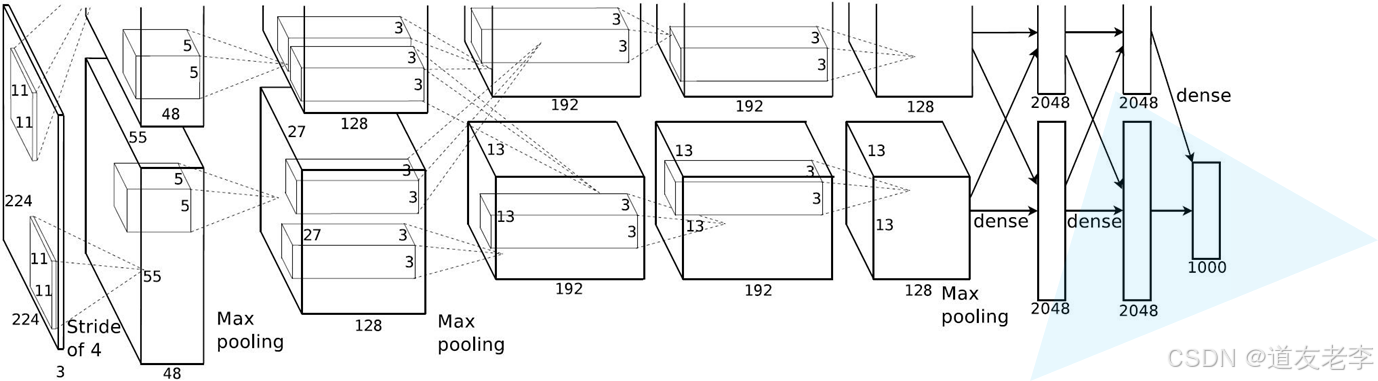
网络亮点

该网络的亮点在于：

1. 首次利用 GPU 进行网络加速训练。
2. 使用了 ReLU 激活函数，而不是传统的 Sigmoid 激活函数以及 Tanh 激活函数。
3. 使用了 LRN 局部响应归一化。
4. 在全连接层的前两层中使用了 Dropout 随机失活神经元操作，以减少过拟合。

过拟合

根本原因是特征维度过多，模型假设过于复杂，参数过多，训练数据过少，噪声过多，导致拟合的函数完美的预测训练集，但对新数据的测试集预测结果差。 过度的拟合了训练数据，而没有考虑到泛化能力。
​

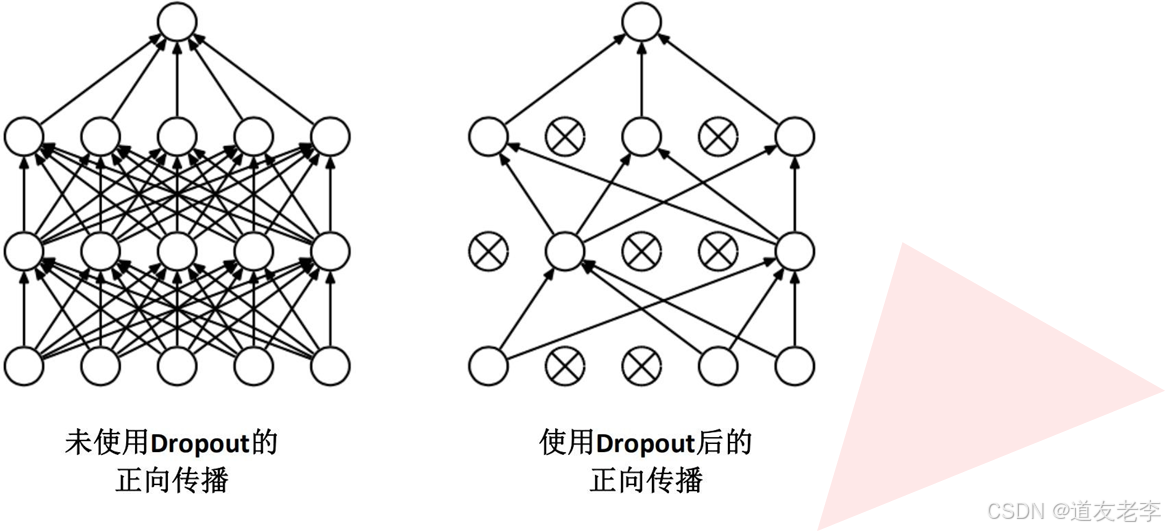
使用 Dropout 的方式在网络正向传播过程中随机失活一部分神经元。

详解

经卷积后的矩阵尺寸大小计算公式为：N = (W − F + 2P ) / S + 1

① 输入图片大小 W×W
② Filter大小 F×F
③ 步长 S
④ padding的像素数 P

Conv1

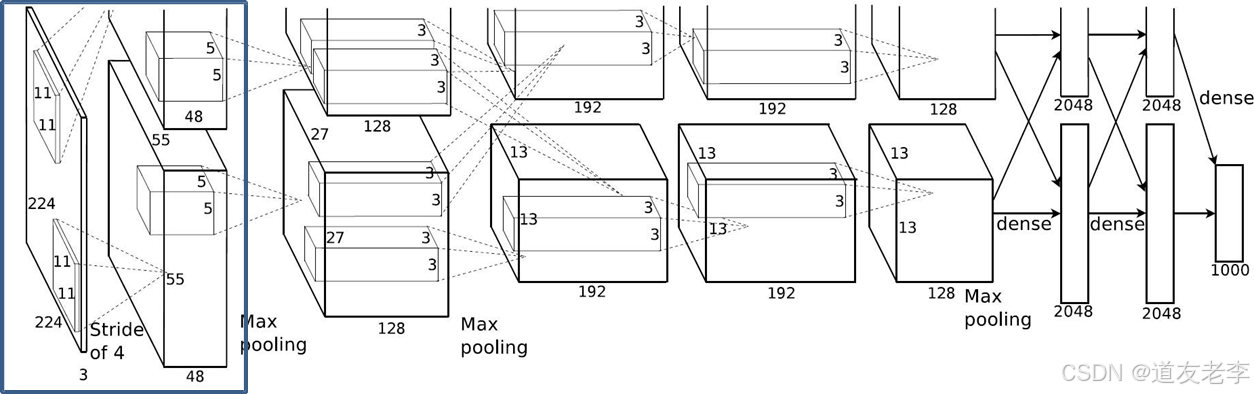
• Conv1:
  • kernels:48*2=96
  • kernel_size:11
  • padding:[1, 2]
  • stride:4
• input_size: [224, 224, 3]
• output_size: [55, 55, 96]
• N = (W − F + 2P ) / S + 1=[224-11+(1+2)]/4+1

Maxpool1

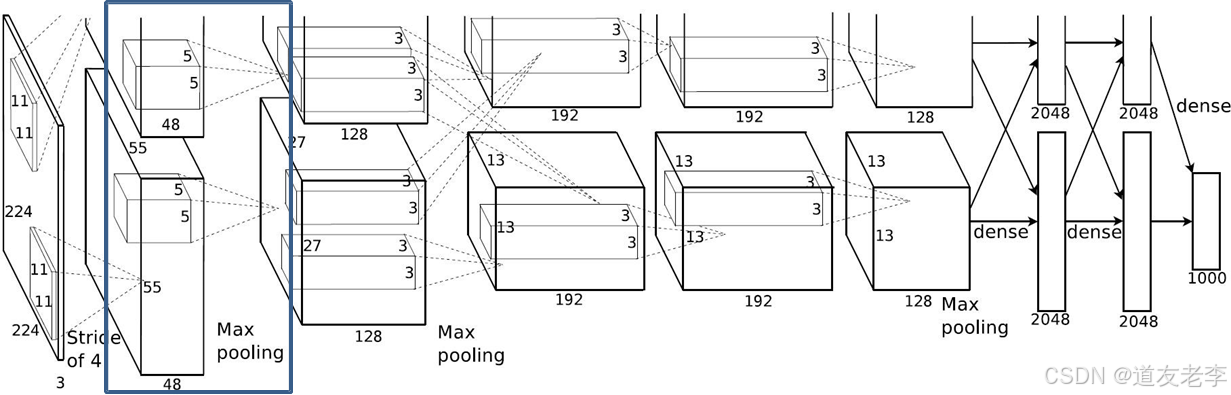
• Maxpool1:

  • kernel_size:3
  • pading: 0
  • stride:2

• input_size: [55, 55, 96]

• output_size: [27, 27, 96]

• N = (W − F + 2P ) / S + 1=(55-3)/2+1

Conv2

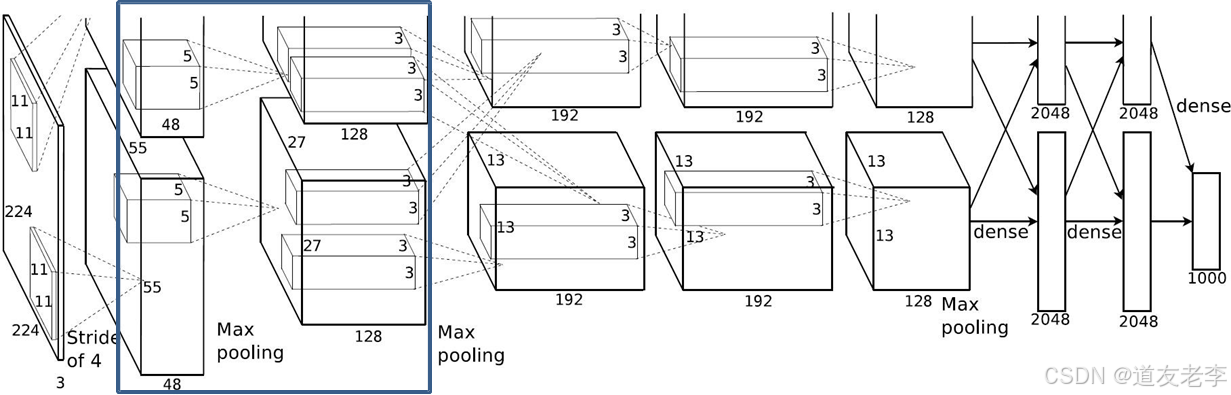
• Conv2:
  • kernels:128*2=256
  • kernel_size:5
  • padding: [2, 2]
  • stride:1
• input_size: [27, 27, 96]
• output_size: [27, 27, 256]
• N = (W − F + 2P ) / S + 1=(27-5+4)/1+1

Maxpool2

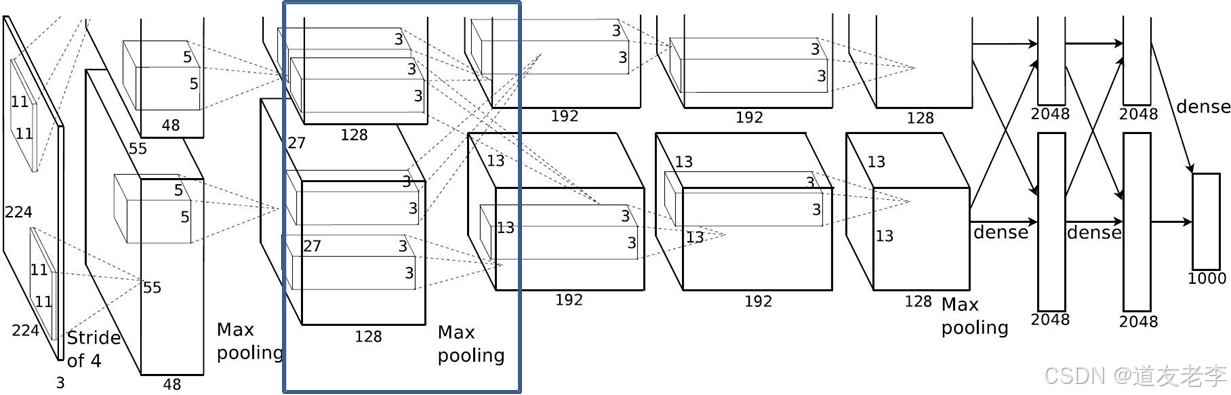
• Maxpool2:

  • kernel_size:3
  • pading: 0
  • stride:2

• input_size: [27, 27, 256]

• output_size: [13, 13, 256]

• N = (W − F + 2P ) / S + 1=(27-3)/2+1

Conv3

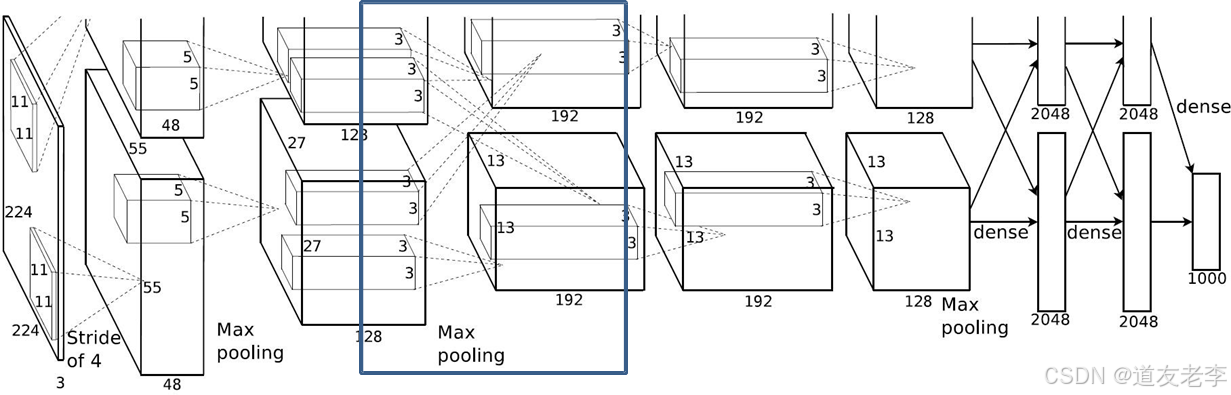
• Conv3:

  • kernels:192*2=384
  • kernel_size:3
  • padding: [1, 1]
  • stride:1

• input_size: [13, 13, 256]

• output_size: [13, 13, 384]

• N = (W − F + 2P ) / S + 1=(13-3+2)/1+1

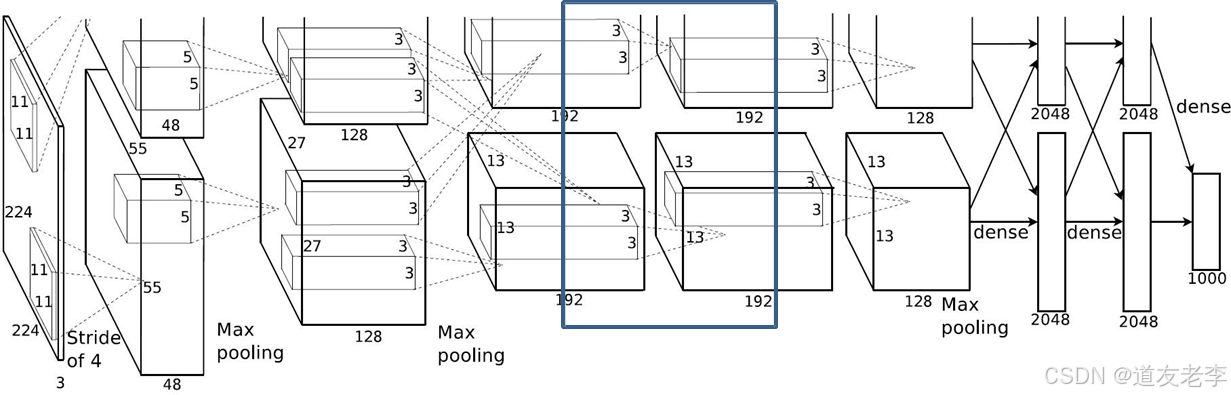
Conv4

• Conv4:

  • kernels:192*2=384
  • kernel_size:3
  • padding: [1, 1]
  • stride:1

• input_size: [13, 13, 384]

• output_size: [13, 13, 384]

• N = (W − F + 2P ) / S + 1=(13-3+2)/1+1

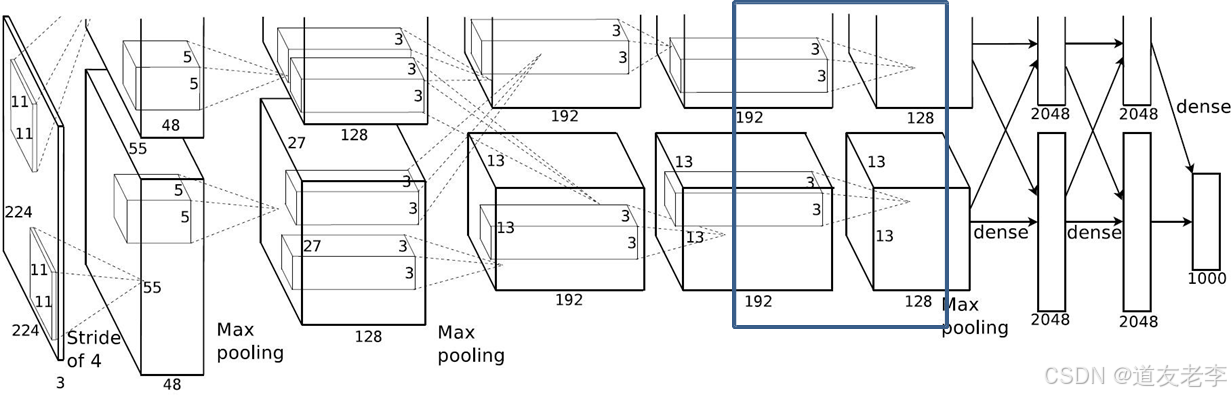
Conv5

• Conv5:

  • kernels:128*2=256
  • kernel_size:3
  • padding: [1, 1]
  • stride:1

• input_size: [13, 13, 384]

• output_size: [13, 13, 256]

• N = (W − F + 2P ) / S + 1=(13-3+2)/1+1

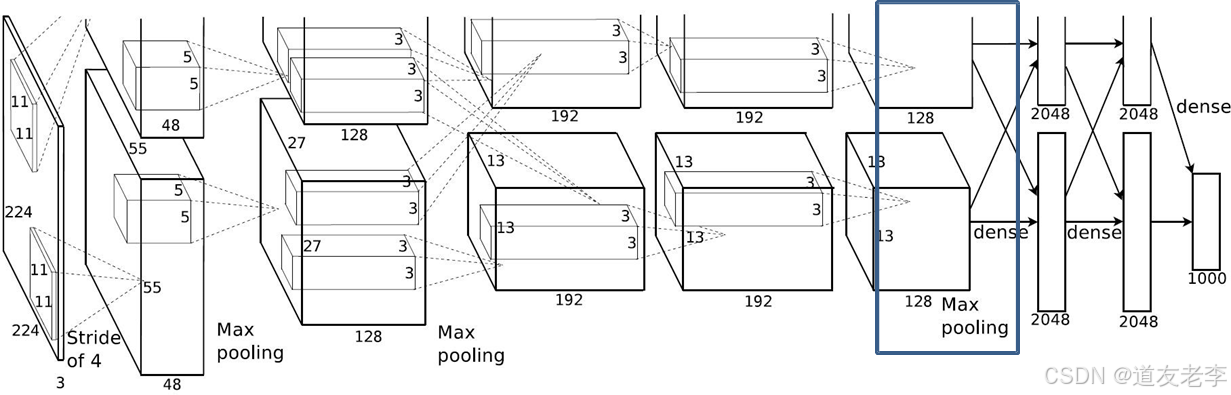
Maxpool3

• Maxpool3:

  • kernel_size:3
  • pading: 0
  • stride:2

• input_size: [13, 13, 256]

• output_size: [6, 6, 256]

• N = (W − F + 2P ) / S + 1=(13-3+2)/1+1